
sb000238
.pdfМИНОБРНАУКИ РОССИИ
–––––––––––––––––––––––––––––––––––––
Санкт-Петербургский государственный электротехнический университет «ЛЭТИ»
–––––––––––––––––––––––––––––––––––––
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Методические указания к самостоятельным работам по одноименной дисциплине
Санкт-Петербург Издательство СПбГЭТУ «ЛЭТИ»
2013
УДК 517.9
Дифференциальные уравнения: метод. указания к самостоятельным работам по одноименной дисциплине / сост.: А. В. Железняк, А. С. Колпаков, А. М. Коточигов. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2013. 32 с.
Содержат основные теоретические сведения и примеры решения задач по темам «Дифференциальные уравнения первого порядка» и «Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами».
Предназначены для студентов первого курса дневной формы обучения.
Утверждено редакционно-издательским советом университета
в качестве методических указаний
© СПбГЭТУ «ЛЭТИ», 2013
ВВЕДЕНИЕ
Возможность моделировать процесс, связывая в уравнение его числовые характеристики со скоростью их изменения, впервые появилась в XVI в. в работах Галилея и к концу XVII в. приобрела четкие очертания в работах Ньютона. Импульс, данный этим открытием научному и техническому прогрессу, невозможно переоценить. Проникновение этих идей в различные сферы человеческой деятельности неуклонно растет и приносит замечательные плоды.
Соотношения, связывающие функцию с ее производной, получили естественное название дифференциальные уравнения. Описание дифференциальным уравнением процесса открывает широкие возможности для контроля и управления его течением. Конечно, это предполагает существование решения дифференциального уравнения. Со времен Ньютона множество людей занималось этой проблемой. Она была и остается очень трудной. Некоторые классы дифференциальных уравнений удается решать аналитически, т. е. по определенному алгоритму, явно выписывая ответ. Почти все такие классы были обнаружены на начальном этапе развития теории. Наряду с этим, чем дальше, тем больше, развиваются численные методы решения дифференциальных уравнений.
Цель данных методических указаний изложить методы решения простейшего типа дифференциальных уравнений, а именно линейных дифференциальных уравнений с постоянными коэффициентами (точное определение будет приведено далее). Такое сужение вопроса оправдано тем, что процесс моделирования, как правило, начинается с упрощенных ситуаций, в которых таких уравнений вполне достаточно. Кроме того, начинать изучение любого нового предмета надо с азов, составляющих его основу. Линейные дифференциальные уравнения с постоянными коэффициентами составляют такую основу для дифференциальных уравнений в целом.
1.ОСНОВНЫЕ ПОНЯТИЯ
1.1. Математическая постановка задачи
Начнем с классификации дифференциальных уравнений. Современная теория, методы решения и приложения настолько обширны, что без терминологии, характеризующей природу уравнений, невозможно обойтись. Дифференциальные уравнения, в которых участвуют функции многих перемен-
3
ных и, следовательно, содержащие частные производные, называют уравне-
ниями в частных производных, или уравнениями математической физики.
Это совершенно самостоятельный раздел теории, использующий более сложный математический аппарат. Здесь такие уравнения не рассматриваются.
Дифференциальные уравнения, содержащие функцию одной переменной и ее производные, называют обыкновенными дифференциальными уравнения-
ми. Это название никак не характеризует сложности задач, а только отделяет уравнения с одной независимой переменной от уравнений в частных производных. Максимальный порядок производной, входящей в уравнение, называется порядком дифференциального уравнения. Так же, как в случае алгебраических уравнений, из дифференциальных можно составлять системы. Совсем просто показать, что всякое дифференциальное уравнение n -го порядка эквивалентно системе n дифференциальных уравнений первого порядка. Это позволяет строить основы обшей теории для уравнений первого порядка.
Дифференциальным уравнением первого порядка называют выражение
вида
F(x, y, y ) 0.
Теорема о неявной функции [1] «сводит» любое такое уравнение к виду y f (x, y).
Отметим и другую форму записи того же уравнения, «уравнивающую в правах» обе переменные:
M (x, y)dx N(x, y)dy 0
(это сразу следует из того, что y dy dx ).
dx ).
Дифференциальные уравнения сложный объект. Необходимо определить, что называется решением дифференциального уравнения. Функция y y(x) решение уравнения y f (x, y), если:
1)y (x);
2)f (x, y(x)) y (x) (т. е. равенство выполнено при всех x ).
Надо иметь в виду, что это определение фактически ссылается на теорему о неявной функции в том смысле, что решением признается любое выражение вида (x, y) 0 и проверка условий 1), 2) осуществляется с помощью этой теоремы.
4
1.2. Геометрический смысл дифференциального уравнения
Для понимания природы дифференциальных уравнений и методов их решения важно знать геометрический смысл решения. Если функция y y(x) решение дифференциального уравнения y f (x, y), проходяще-
го через точку (x0, y0), то в этой точке график решения имеет касательную:
y y0 f (x0, y0)(x x0), y0 y(x0).
Следовательно, даже не зная решения уравнения, можно провести касательную к решению в любой точке, где определена функция f . Это обстоятельство позволяет придать геометрический смысл дифференциальному уравнению. Пусть в каждой точке (x, y) плоскости (или некоторого подмножества плоскости) задан вектор (x, f (x, y)) . Тогда решением уравнения будет любая кривая, которая в каждой точке имеет касательную, содержащую заданный в точке вектор. Рассмотрим примеры, иллюстрирующие это утверждение.
Пример 1. Простейшее дифференциальное уравнение y f (x) . Это
уравнение можно рассматривать как определение первообразной, и поэтому его решением будет функция
x
y(x) y(x0) f (x1)dx1 .
x0
Постоянная y0 y(x0) может быть произвольной, значит, множеством всех
решений будет соответствующий неопределенный интеграл. Опишем геометрический смысл данного дифференциального уравнения: в каждой точке (x, y) плоскости задан вектор (1, f (x)); требуется провести кривую, касательная которой совпадает с направлением вектора. Отметим важное свойство полученных решений: через каждую точку плоскости проходит одноединственное решение.
Пример 2. Геометрический метод решения дифференциальных уравнений.
Прямое использование такого метода возможно только для очень простых множеств направлений. Примером такой ситуации может служить множество направлений, у которого в каждой точке вектор ортогонален отрезку, соединяющему точку с началом координат. Заметим, что такое определение теряет смысл в начале координат, поэтому эту точку придется исключить. Для любой другой точки (x0, y0) решением, проходящим через нее, будет окруж-
5
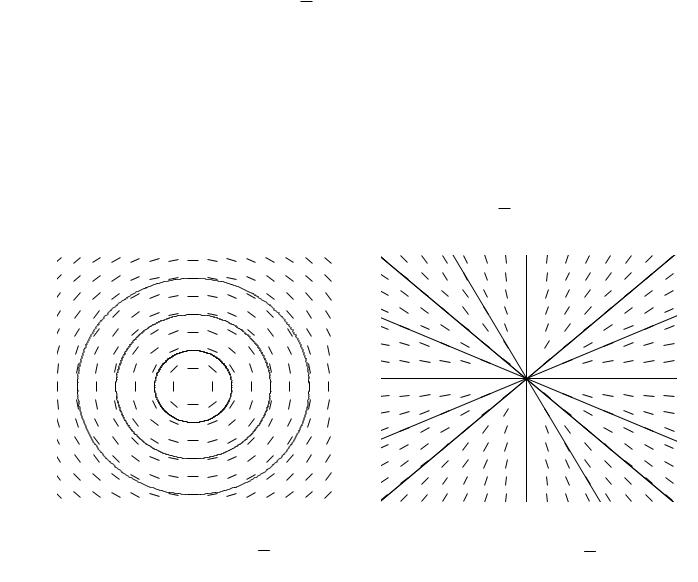
ность x2 y2 x2 y2 |
(рис. |
1.1). И в этом примере через каждую точку |
|
|||||
0 |
0 |
|
|
|
|
|
|
|
плоскости, кроме начала координат, проходит одно-единственное решение. |
|
|||||||
Нетрудно написать соответствующее дифференциальное уравнение: |
|
|||||||
|
|
|
y x , или |
xdx ydy 0 . |
|
|
|
|
|
|
|
|
y |
|
|
|
|
Пример 3. Данный пример дополняет предыдущий (рис. 1.2). В каждой |
|
|||||||
точке вектор совпадает с вектором, начинающимся в этой точке и заканчи- |
|
|||||||
вающимся в начале координат. Решение здесь совсем очевидно это прямые |
|
|||||||
вида y kx , точнее ax by 0. Как и раньше, через каждую точку, кроме на- |
|
|||||||
чала координат, проходит одно решение. Однако в особой точке (в начале |
|
|||||||
координат) картина совсем иная – через нее проходят все решения. Соответ- |
|
|||||||
ствующее дифференциальное уравнение имеет вид y y , или |
ydx xdy 0. |
|
||||||
|
|
|
|
|
x |
|
|
|
2 |
|
|
|
|
2 |
|
|
|
Рис. 1.1. Геометрический смысл и решения |
-2-2 Рис. 1.2. Геометрический смысл и решения |
2 |
||||||
-2-2 |
|
|
x |
2 |
Пример 4. Бывают и более слож |
|
||
уравнения |
y |
|
|
|
y |
y |
|
|
y |
|
уравнения |
x |
|
||||
|
|
|
|
|
||||
Пример 4. Бывают и более сложные примеры. На рис. 1.3 изображен |
|
|||||||
геометрический смысл и решения уравнения y x y2. Известен факт, что
эти решения невозможно выписать не только в явном, но даже и в неявном виде. Читателю предлагается в качестве упражнения доказать, что нулевой изоклиной для данного дифференциального уравнения (т. е. кривой, в каждой точке которой какое-то решение имеет горизонтальную касательную) являет-
ся кривая x y2 (для этого достаточно просто приравнять производную к нулю). Можно также проверить, что кривая перегибов в данном случае (т. е.
6
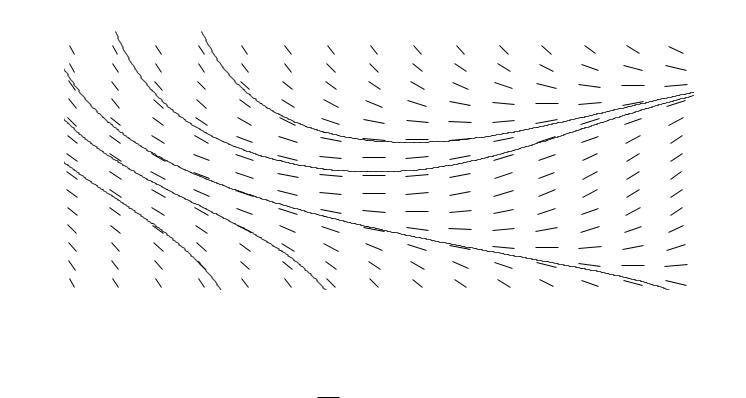
2 |
|
1.5 |
|
1 |
|
0.5 |
|
0 |
|
-0.5 |
|
-1 |
|
-1.5 |
|
-2 |
Рис. 1.3. Геометрический смысл и решения уравнения y x y2 |
-2 |
2 |
кривая, каждая точка которой является точкой перегиба какого-либо из ре-
шений) это кривая x y2 21y (сначала нужно выразить вторую произ-
водную через x и y , а затем приравнять ее к нулю).
1.3.Условия единственности решения. Задача Коши
Вбольшинстве ситуаций, возникающих при решении дифференциальных уравнений, важно иметь дополнительные условия, гарантирующие единственность решения. Приведенные в 1.2 примеры позволяют предположить, что для этого достаточно знать, что решение проходит через заданную точку области, где определена функция f (x, y) . Эта гипотеза «почти верна», точ-
нее справедлива следующее утверждение [2], называемое теоремой сущест-
вования и единственности решения дифференциального уравнения: если в некоторой области плоскости функции f (x, y) и f y (x, y) непрерывны, то
через каждую точку области проходит одно решение дифференциального уравнения y f (x, y).
Ситуация, когда решение дифференциального уравнения единственно, очень важна, и для нее есть специальное название задача Коши:
y f (x, y), y(x0) y0,
которая состоит в том, чтобы найти решение дифференциального уравнения, удовлетворяющее начальному условию (проходящее через заданную точку).
7

Теорема единственности и постановка задачи Коши переносятся на дифференциальные уравнения высших порядков:
y(n) f x, y, y , |
, y(n 1) , y(x0) y0, |
, y(n 1)(x0) yn 1 |
и на системы дифференциальных уравнений:
|
y |
f (x, y , |
, y |
n |
), y (x ) y |
, |
|
||||
1 |
1 |
|
1 |
0 |
1, 0 |
|
|
||||
|
|
|
...; |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
y |
f (x, y , |
, y |
n |
), y |
n |
(x ) y |
n, 0 |
. |
|||
|
n |
1 |
|
|
0 |
|
|
||||
Условия теоремы можно ослабить, но это требует введения дополнительных определений. Доказательство теоремы основано на построении последовательности приближений к решению. Доказательство сходимости такой последовательности трудное и неконструктивное. Устанавливается только факт сходимости, алгоритма поиска решения не предлагается. Однако методы построения приближенного решения служат базой для многочисленных приемов численного решения задачи Коши. Далее рассмотрим наиболее важный алгоритм [3].
|
|
|
1.4. Метод Эйлера (метод касательных) |
||||||
|
|
Задача Коши |
y f (x, y), y(x0) y0 дает возможность описать каса- |
||||||
|
тельную к решению y y0 f (x0, y0)(x x0). Возьмем число x1, находящее- |
||||||||
|
ся от x0 на малом расстоянии h , и поставим новую задачу Коши: |
||||||||
|
|
|
|
|
|
|
|
|
y f (x, y), y(x1) y1, |
|
|
|
|
|
|
|
|
|
где |
1.2 |
|
|
|
|
|
|
|
|
y1 y0 f (x0, y0)h , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т. е. заменим решение исходной задачи |
|
|
|
|
|
|
|
|
|
Коши касательной. Продолжая этот |
|
|
|
|
|
|
|
|
|
процесс, получим ломаную Эйлера – |
|
(x0, y0) |
|
|
|
|
|
|
приближенное решение задачи Коши. |
|
|
|
|
|
|
|
|
Можно доказать, что ломаные сходятся |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к решению дифференциального урав- |
0 |
|
0.2 |
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
|
-1 |
-0.8 |
-0.6 Рис-0.4. 1.4.- Ломаные Эйлера |
|
|
нения (при стремлении длины звеньев |
||||
|
для задачи Коши |
y x |
, |
y(x0) y0 |
|
||||
|
|
ломаной к нулю). Сказанное наглядно |
|||||||
|
|
|
|
y |
|
|
|
|
продемонстрировано на рис. 1.4 (разби- |
|
|
при различных h |
|
|
|
||||
|
|
|
|
|
|
|
|
|
рается уравнение из примера 2). |
8
Стоит отметить, что в численных методах метод Эйлера не применяют изза плохой сходимости. Однако небольшая модификация метода, позволяющая использовать для построения аналога касательной несколько точек, исправляет этот недостаток. Такие методы называются методами Рунге Кутты.
Явное (аналитическое) решение дифференциального уравнения – ситуация довольно редкая (основным типам уравнений первого порядка, интегрируемым в квадратурах, посвящены 2.1 2.4). Объемный справочник [4] дает правильное представление об этом. Из многочисленных примеров в нем видно, что стоит немного изменить уравнение и возможность его явного решения исчезает. При построении моделей тех или иных процессов, основанных на дифференциальных уравнениях, очень важно на начальном этапе так упростить модель, чтобы описывающее ее дифференциальное уравнение было достаточно простым. К таковым в первую очередь принадлежат линейные дифференциальные уравнения с постоянными коэффициентами. Понимание того, как можно получить решение такого уравнения, необходимо для правильного использования таких моделей.
С точки зрения математики эти уравнения хороши тем, что сравнительно легко переписываются в эквивалентные линейные алгебраические решения. Решению таких дифференциальных уравнений посвящены 3.1 3.3.
2. ИНТЕГРИРУЕМЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
2.1. Уравнения с разделяющимися переменными
Уравнениями с разделяющимися переменными называются уравнения,
которые при помощи тождественных преобразований могут быть приведены к виду
g(x)dx h(y)dy
(отсюда и происходит название переменные как бы «разделились»). Теорема об интеграле с переменным верхним пределом гарантирует наличие первообразных G(x) и H (y) , для которых выполняется равенство
G(x) H (y) C.
Теперь из теоремы о неявной функции вытекает существование функции y y(x), обращающей это равенство в тождество. (На практике зачастую
данный шаг либо затруднителен, либо не приводит к существенному упрощению записи ответа. В этом случае его опускают.)
9
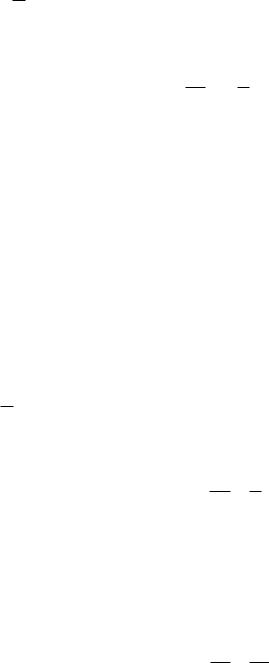
Продемонстрируем приведенный алгоритм на примерах из предыдущего параграфа:
1. y xy .
Распишем производную через дифференциалы. Получаем соотношение dydx xy .
Далее перенесем все y в левую часть, а все x в правую. Заметим, что при
делении на x решения не теряются (кривая x 0 не являлась решением исходного уравнения, поскольку dx стоял в знаменателе). Следовательно,
ydy xdx .
После интегрирования приходим к окончательному ответу:
y2 |
|
x2 |
C , или |
x2 y2 C . |
2 |
|
|||
2 |
|
|
||
Произвольная постоянная была переобозначена. Это допустимо, поскольку 2C, как и C, принимает любые значения.
2. y xy .
Распишем производную через дифференциалы. Получаем соотношение dydx xy .
Далее перенесем все y в левую часть, а все x в правую. Заметим, что при делении на y могло потеряться решение y 0. Подставив его в исходное уравнение, получим 0 0, т. е. верное соотношение. Таким образом, y 0 действительно является решением исходного уравнения. Следовательно,
dy dx ,
y xy 0,
где квадратными скобками обозначено объединение множеств решений. Вычисляя интегралы, получаем:
ln | y | ln | x | C,
y 0,
10
