
mat_an_lektsia_nesob_int_2roda
.pdf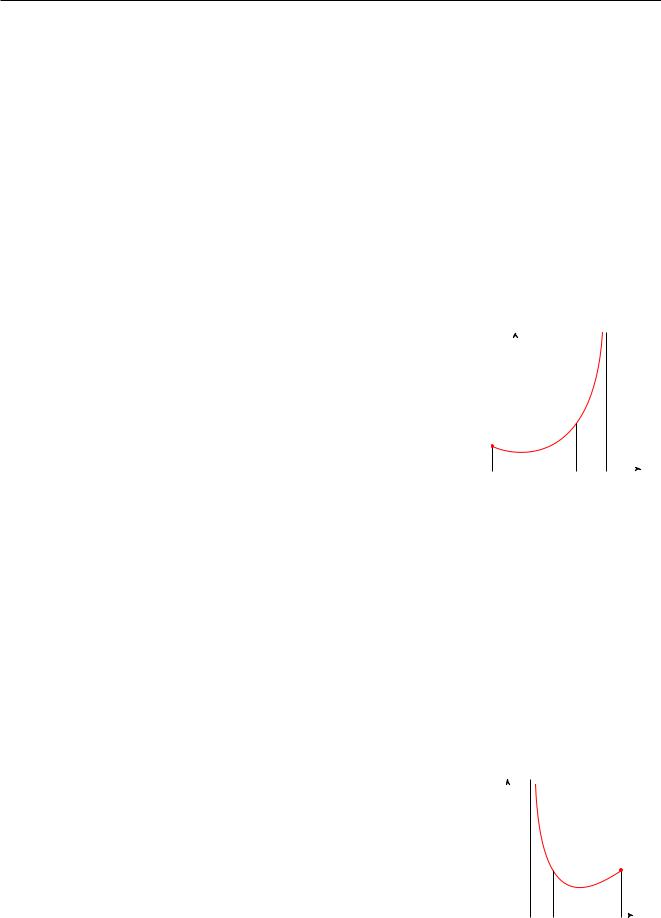
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
§ 2. Несобственные интегралы II рода
b
R
Для определенного интеграла f(x)dx длина отрезка [a; b] должна быть конечной, а необ-
a
ходимым условием интегрируемости функции является ограниченность функции на этом отрезке. Если убрать условие конечности отрезка, то получим понятие несобственного интеграла I рода, как было показано на прошлой лекции. Теперь предположим, что не выполняется необходимое условие интегрируемости функции.
Пусть функция f(x) непрерывна на промежутке [a; b). Будем называть точку b особой
для функции f(x), если
x |
lim |
0 |
f(x) = |
1 |
: |
|
|
|
|
|
|
(2.1) |
||
b |
|
|
|
|
|
|
|
|
|
|||||
|
! |
|
|
|
|
|
|
|
|
|
|
|
|
|
Отступим (рис. 2.1) от особой точки b влево на некоторую ве- |
|
y |
|
|
|
|
||||||||
|
|
|
|
|||||||||||
личину " > 0 так, чтобы при этом точка b " 2 (a; b). Так как |
|
|
|
|
|
|
||||||||
рассматриваемая нами функция f непрерывна на промежутке |
|
|
|
y = f(x) |
|
|
||||||||
[a; b), то она непрерывна на любом отрезке [a; b "] [a; b); а |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|||||||||
значит, функция интегрируема на этом отрезке, т. е. существу- |
|
|
|
|
|
|
||||||||
b " |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ет определенный интеграл f(x)dx. Значение этого интеграла, |
|
|
|
|
|
|
||||||||
помимо самой функции f, Raточек a и b, зависит от выбранного |
|
|
|
|
|
x |
||||||||
a |
|
|
b " b |
|
||||||||||
|
|
|
|
|||||||||||
значения числа "; тем самым мы получим некоторую функцию |
|
|
|
Рис. 2.1 |
|
|
||||||||
|
|
|
|
|
|
|||||||||
b " |
|
|
|
|
|
|
|
" при этом приближается к точке b |
||||||
I(") = f(x)dx: Устремим теперь " к нулю (точка b |
|
|||||||||||||
слева) иRa посмотрим к чему будет стремиться значение функции I("); т. е. рассмотрим |
|
|
||||||||||||
|
|
|
|
b " |
|
|
|
|
|
|
|
|
|
|
lim I " |
|
|
lim |
f |
|
x |
dx: |
|
|
|
|
|
|
|
"!+0 ( ) = |
"!+0 Za |
|
( |
) |
|
|
|
|
|
(2.2) |
||||
Независимо от того, существует ли этот предел, будем называть его несобственным ин-
тегралом II рода и обозначать |
b |
|
|
|
|
|
|
|
|
|
|||||
f(x)dx. Если при этом предел существует и конечен, то |
|||||||||||||||
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
несобственный интеграл |
называется сходящимся, иначе расходящимся. |
|
|
||||||||||||
|
|
|
R |
|
|
|
|
|
|
|
|
|
|||
Аналогично вводится понятие несобственного интеграла II ро- |
y |
|
|
|
|
||||||||||
да, в случае, когда функция непрерывна на промежутке (a; b] |
|
y = f(x) |
|
|
|||||||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и точка a особая (рис. 2.2). При этом от особой точки a надо |
|
|
|
|
|
|
|||||||||
отступить вправо на некоторую величину "; но так, чтобы точка |
|
|
|
|
|
|
|||||||||
a + " была внутри интервала (a; b); а затем устремить " к нулю |
|
|
|
|
|
|
|||||||||
b |
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
Za |
|
|
|
|
"!+0aZ+" |
|
|
|
|
|
|
|
|
x |
|
( |
) |
|
= |
( |
) |
|
|
|
|
a a + " |
|
||||
f |
|
x |
dx |
|
lim |
f |
|
x |
dx: |
|
|
|
b |
||
|
|
|
|
|
|
||||||||||
Рис. 2.2
1
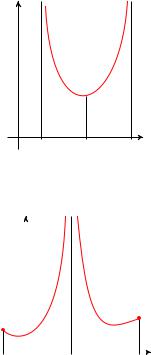
Если для непрерывной на интервале (a; b) функции f особыми |
|
||||
являются обе точки a и b (рис. 2.3), то, выбрав произвольную |
|
||||
точку c из интервала (a; b), представим (сначала формально) |
y |
||||
несобственный интеграл II рода в виде суммы двух несобствен- |
|
||||
ных интегралов |
|
|
|
|
|
b |
|
c |
b |
|
|
Za |
f(x)dx = Za |
f(x)dx + Zc |
f(x)dx: |
(2.3) |
|
y =
a |
c |
x |
|
b |
|||
|
|
Если каждый из интегралов, стоящих в правой части (2.3), схо- |
|
Рис. 2.3 |
|
|
||
|
b |
|
|
|
|
|
дится, то и интеграл f(x)dx сходится, и это равенство выпол- |
y |
|
|
|
||
няется. Если хотя быRaодин из интегралов в правой части (2.3) |
|
|
|
|
||
расходится, то расходящимся будет и интеграл в левой части. |
|
y = f(x) |
|
|
||
Если функция непрерывна на отрезке [a; b] за исключением осо- |
|
|
|
|
||
бой точки c, лежащей внутри интервала (a; b), то в этом случае |
|
|
|
|
||
также представим несобственный интеграл II рода в виде сум- |
|
|
|
|
x |
|
a |
|
c |
|
|||
|
|
|
b |
|||
мы двух несобственных интегралов (2.3). Сходящимся интеграл |
|
Рис. 2.4 |
||||
|
|
|
||||
b |
|
|
|
|
|
|
f(x)dx будет тогда и только тогда, когда сходится каждый из |
|
|
|
|
||
a |
в правой части равенства (2.3). |
|
|
|
|
|
интеграловR |
|
|
|
|
||
Примечание 1. Аналогично вводится понятие несобственного интеграла II рода для функ-
ций, имеющих на отрезе [a; b] любое конечное число особых точек.
Примечание 2. ¾Внешний вид¿ несобственного интеграла II рода такой же, как и у определенного интеграла. Поэтому, чтобы отличить один от другого, надо выяснить, есть ли у подынтегральной функции особые точки на отрезке [a; b]: Рассмотрим, например, два инте-
грала
|
|
|
|
|
I1 |
1 |
|
x ; |
|
|
I2 |
|
|
|
2 |
|
x : |
|
|
|
|
|
|
|
|
= Z0 |
|
|
= Z1 |
|
|
||||||||||
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
dx |
|
|
|||
Подынтегральная функция f(x) = 1 |
одинакова. Точка x = 0 для этой функции являет- |
|||||||||||||||||||
|
|
|
|
|
|
x |
|
|
lim |
1 = |
|
: |
|
|
|
|
|
|
||
ся точкой разрыва второго рода, так как |
1 |
Следовательно, эта точка является |
||||||||||||||||||
x!0 |
x |
|
||||||||||||||||||
особой для интеграла I1: Поэтому I1 несобственный интеграл II рода. Вычислим его по |
||||||||||||||||||||
определению |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
x |
1 |
x = |
"!+0 |
|
j" = |
"!+0 |
|
|
|
|
"!+0 |
|
1 |
|||||
|
1 = Z |
= "!+0 Z |
|
|
|
|
||||||||||||||
I |
|
dx |
lim |
dx |
lim |
ln x |
|
1 |
lim (ln 1 |
|
|
ln ") = lim ( |
|
ln ") = + ; |
||||||
|
|
|
|
|
|
|
|
|
||||||||||||
0"
т.е. I1 расходится.
На отрезке же [1; 2] функция f(x) непрерывна, следовательно, I2 это обычный определен-
ный интеграл, который вычисляется по формуле Ньютона–Лейбница
2 |
x = ln xj12 |
= ln 2 ln 1 = ln 2: |
I2 = Z1 |
||
|
dx |
|
2
Проверять функцию на интегрируемость на отрезке, по которому считается интеграл, надо всегда. Формальное применение формулы Ньютона–Лейбница может привести к ошибкам, как при нахождении, например, следующего интеграла
1 |
|
|
|
|
|
|
|
Z |
dx |
1 |
1 |
|
|||
|
= |
|
|
1 = 2 < 0: |
|||
x2 |
x |
|
|||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значение интеграла получилось отрицательным, хотя подынтегральная функция очевидно положительна. Ошибка возникла из-за того, что подынтегральная функция неограничена на отрезке интегрирования [ 1; 1]; а следовательно, неинтегрируема на этом отрезке. Рассмотренный интеграл представляет из себя несобственный интеграл II рода с особой точкой x = 0. Так как особая точка лежит внутри отрезка интегрирования, то интеграл мы должны представить в виде суммы двух
1 |
x2 |
0 |
x2 |
1 |
x2 : |
|
Z |
= Z |
+ Z |
||||
|
dx |
dx |
dx |
|||
1 |
|
1 |
|
0 |
|
|
Исследуем на сходимость, например, второй из них
1 |
x2 |
= |
"!+0 |
1 |
x2 |
"!+0 |
x |
" |
! |
"!+0 |
|
" |
1 |
|||
|
|
|||||||||||||||
Z |
dx |
|
Z |
dx |
|
1 |
1 |
|
|
1 |
|
|||||
|
|
lim |
|
|
= lim |
|
|
|
|
= lim |
1 + |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0"
R1 dx
т. е. интеграл расходится. Значит, расходится и интеграл 1 x2 :
Интеграл вида
Z
sinx xdx
0
не является несобственным II рода, хотя казалось бы, что точка x = 0 должна быть особой для подынтегральной функции. Но, если вспомнить ¾замечательный¿ предел
lim sin x = 1 6= 1;
x!0 x
то получим, что x = 0 вовсе не особая точка. Доопределив подынтегральную функцию в точке x = 0 значением, равным 1, получим непрерывную, а следовательно, и интегрируемую функцию. Значит, это определенный интеграл, а не несобственный.
Интеграл вида
1
Z dx
xp
0
не является несобственным II рода при p < 0, так как
lim 1 = 0:
x!+0 xp
ДЗ: Исследуйте этот интеграл при p 0:
3
Свойства несобственных интегралов II рода
1. Если интеграл |
b |
b |
f(x)dx сходится, то для любой константы C интеграл Cf(x)dx схо- |
||
дится, причем |
Ra |
Ra |
|
b |
b |
|
Z |
Z |
Cf(x)dx = C f(x)dx:
|
|
a |
a |
|
2. Если интеграл |
b |
f(x)dx расходится, то для любой константы C = 0 интеграл |
b |
|
Ra |
Cf(x)dx |
|||
расходится. |
|
6 |
Ra |
|
3. Пусть точка b является особой для функций f(x) и g(x), непрерывных на промежутке [a; b):
причем |
b |
|
b |
|
b |
|
|
|
Ra |
f(x)dx и |
Ra |
|
Ra |
(f(x) |
g(x)) dx; |
||
Если сходятся оба интеграла |
g(x)dx, то сходится и интеграл |
|
||||||
|
b |
|
|
b |
b |
|
|
|
Za |
(f(x) g(x)) dx = Za |
f(x)dx Za |
g(x)dx: |
|
|
|
||
bb
RR
Примечание. Если оба интеграла f(x)dx и g(x)dx расходятся, то про сходимость
aa
b
R
интеграла (f(x) g(x)) dx ничего утверждать нельзя. Можно привести примеры таких
a
bb
RR
функций f(x) и g(x), для которых f(x)dx и g(x)dx расходятся, но, например, интеграл
|
a |
a |
|
|
|
b |
|
b |
|
|
|
(f(x) + g(x)) dx сходится, а интеграл |
(f(x) g(x)) dx расходится. |
||||
a |
|
a |
f(x), непрерывной на промежутке [a; b): |
||
4.R |
Пусть точка b является особой для функцииR |
||||
Точка c произвольная из интервала (a; b): Тогда интегралы |
b |
b |
|||
f(x)dx и |
f(x)dx ведут себя |
||||
одинаково, т. е. либо оба сходится, либо оба расходятся. |
Ra |
Rc |
|||
5. Пусть точка b является особой для функций f(x) и g(x), непрерывных на промежутке
[a; b): Для всех x из этого промежутка выполняется неравенство f(x) g(x): Если при этом
bb
RR
сходятся интегралы f(x)dx и g(x)dx; то справедливо неравенство
aa
bb
ZZ
f(x)dx g(x)dx:
aa
6.(обобщенная формула Ньютона–Лейбница)
Пусть точка b является особой для функции f(x), непрерывной на промежутке [a; b): Функция F (x) является первообразной для f(x) на промежутке [a; b): Тогда
b
Z
f(x)dx = F (b) F (a);
a
где F (b) = F (b 0) = lim F (x):
x!b 0
4

Рассмотрим далее функцию f(x); непрерывную на промежутке [a; b) с особой точкой b: По
b
R
определению, сходимость интеграла f(x)dx следует из существования конечного предела
a
(2.2). Запишем критерий Коши существования конечного предела справа функции I(") в
точке " = 0:
8"~ > 0 9 (~") > 0 : 8"1; "2 2 O+(0) ) jI("1) I("2)j < ":~
Применим это утверждение для функции I(") и воспользуемся свойством аддитивности
по отрезку для определенного интеграла
|
|
|
|
|
|
b "1 |
b "2 |
|
b "1 |
|
|
|
|
|
|
|||
|
|
|
I("1) I("2) = |
Za |
f(x)dx Za |
f(x)dx = |
Z |
f(x)dx: |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
b "2 |
|
|
|
|
|
|
|
Получим следующее утверждение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Теорема 1 (Критерий Коши сходимости несобственного интеграла II рода) |
||||||||||||||||||
|
f(x)dx |
|
сходится |
|
"~ > 0 |
|
(~") > 0 : |
"1; "2 |
O+(0) |
|
|
|
|
f(x)dx |
< ":~ |
|||
Z |
b |
|
|
|
|
|
|
|
|
|
|
|
|
b "1 |
|
|
||
|
|
|
, 8 |
|
|
|
9 |
8 |
2 |
|
) |
Z |
|
|
||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
"2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Исследовать интеграл на сходимость по определению или с помощью критерия Коши может быть довольно трудно. В некоторых случаях проще воспользоваться признаками схо-
димости, которые будут приведены далее.
Теорема 2 (признак сравнения)
Пусть точка b является особой для функций f(x) и g(x), непрерывных и неотрицатель-
ных на промежутке [a; b): И для всех x из этого промежутка выполняется неравенство
|
|
0 f(x) g(x); x 2 [a; b): |
||
Тогда: |
b |
b |
|
|
1) Если |
Rab g(x)dx сходится, то и Ra |
fb(x)dx сходится. |
||
2) Если |
Ra |
f(x)dx расходится, то и |
Ra |
g(x)dx расходится. |
Можно воспользоваться и следующим утверждением
Теорема 3 (признак сравнения в предельной форме)
Пусть точка b является особой для функций f(x) и g(x), непрерывных и неотрицательных на промежутке [a; b); причем в некоторой левой полуокрестности точки b функция g(x) не обращается в нуль. Тогда, если существует конечный предел
lim f(x)
x!b 0 g(x)
b |
b |
R |
R |
то интегралы g(x)dx и |
f(x)dx ведут себя одинаково, т. е. либо оба сходится, либо оба |
a |
a |
расходятся. |
|
5

Признаки сравнения работают только для функций, неотрицательных на промежутке
[a; b): Если же функция неположительна на этом промежутке, то ее просто можно умножить на константу C = 1; тем самым поменяв знак на противоположный. Сходимость/расходимость интеграла при этом не изменится.
Если же функция не является знакопостоянной на промежутке [a; b); то интеграл на сходимость можно исследовать с помощью следующей теоремы.
Теорема 4 (об абсолютной сходимости)
Пусть точка b является особой для функции f(x), непрерывной на промежутке [a; b):
Тогда, если
b |
|
b |
Za |
jf(x)jdx сходится ) Za |
f(x)dx сходится: |
Сходимость интеграла в этом случае называется абсолютной.
Примечание. В обратную сторону утверждение неверно. Существует такие функции, от которых интеграл сходится, но при этом интеграл от модуля функции расходится. Сходимость интеграла в этом случае называется условной.
Бета-функция Эйлера
Бета-функцией Эйлера (B-функцией) называется функция, заданная как интеграл вида
1
Z
B(x; y) = tx 1(1 t)y 1dt:
0
Функция определена при x > 0; y > 0:
Основные свойства.
1. |
(свойство симметрии) |
|
|
|
|
|
|
|
B(x; y) = B(y; x) |
|
|
||||
2. |
(формула понижения) |
x 1 |
|
|
|
|
|
|
B(x; y) = |
|
|
B(x |
|
1; y) |
|
|
x + y 1 |
||||||
|
|
|
|
||||
3.
B(x; y) = (x) (y);(x + y)
где (x) гамма-функция Эйлера.
7 апреля 2020 г.
6
