mat_an_lektsia_funk_mn_per_1

МАТЕМАТИЧЕСКИЙ АНАЛИЗ

Глава ? . Функции многих переменных

§ 1. Основные понятия

Каждый упорядоченный набор (x1; x2; :::; xm) из m действительных чисел называется точкой m-мерного координатного пространства Rm и обозначается X(x1; x2; :::; xm), числа x1; x2; :::; xm называются координатами точки X. Если расстояние между точками

A(a1; a2; :::; am) и B(b1; b2; :::; bm) определяется формулой

q

(A; B) = (a1 b1)2 + (a2 b2)2 + ::: + (am bm)2;

то координатное пространство называется евклидовым и обозначается Em.

Пусть дана точка X0 2 Em и некоторое неотрицательное число r: Множество точек

X(x1; x2; : : : ; xm) 2 Em, для которых выполняется неравенство (X; X0) r; называется

m-мерным шаром радиуса r с центром в точке X0: Если неравенство является строгим, то шар называется открытым. Если неравенство заменить на равенство (X; X0) = r, то множество таких точек называется m-мерной сферой.

Открытый шар радиуса " с центром в точке X0 называется "-окрестностью точки

X0 и обозначается O"(X0):

в отличии от внутренней точки, которая по определению должна сама принадлежать множеству D; граничная точка может этому множеству и не принадлежать. Множество все граничных точек называется гра-

ницей множества D: Множество D; содержащее все свои граничные точки, называется

замкнутым. Множество, полученное присоединением к множеству D всех его граничных точек, называется замыканием множества D и обозначается обычно D: Если все точки множества D являются внутренними, то такое множество называется открытым.

Пример 1. Определить является ли множество D; представляющее из себя отрезок, открытым или замкнутым в пространстве: 1) E; 2) E2:

Решение. 1) В первом случае множество D = fx 2 R : x 2 [a; b]g, где a и b некоторые действительные числа (рис. 1.2). В одномерном случае "-окрестность точки x 2 R это интервал (x "; x + "): Если взять любую точку x 2 (a; b); то можно подобрать такое число

"; что O"(x) [a; b]; т. е. любая точка интервала (a; b) является внутренней (рис. 1.3). Точка

1

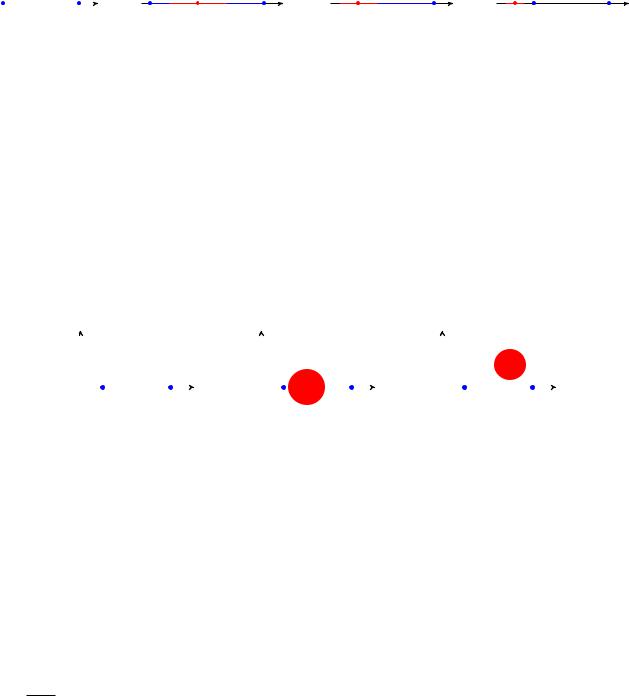
a является граничной точкой множества D; так как в любой ее окрестности (рис. 1.4) содержатся точки, принадлежащие множеству D (правая полуокрестность), так и точки, не принадлежащие D (левая полуокрестность). Аналогично доказывается, что и точка b является граничной точкой множества D: Точки, лежащие вне отрезка [a; b]; не могут быть по определению внутренними для множества D; так как не принадлежат этому множеству. Не могут они быть и граничными, так как для любой точки x 62[a; b] можно подобрать значение

"; такое что в "-окрестности точки x не будет ни одной точки множества D (рис. 1.5). В итоге, множество D замкнутое, так как содержит обе свои граничные точки.

2) Во втором случае без ограничения общности можно считать, что отрезок лежит на оси абсцисс, т. е. множество D = f(x; y) 2 R2 : x 2 [a; b]; y = 0g, где a и b некоторые действительные числа (рис. 1.6). В двумерном случае "-окрестность точки M 2 R2 это открытый круг (круг без точек на самой окружности) с центром в точке M. Любая точка M 2 D

является граничной точкой множества D; так как в любой ее окрестности (рис. 1.7) содержатся точки, принадлежащие множеству D, так и точки, не принадлежащие D. Если же точка M 62D, то она не является граничной, так как можно подобрать такую окрестность этой точки, в которой не будет ни одной точки из множества D (рис. 1.8). Следовательно, по определению, множество D замкнутое.

ДЗ: Рассмотреть множество D = [a; b) в E и E2: Определить, какие точки являются внутренними; граничными. Выяснить, является ли множество открытым или замкнутым.

Множество D называется ограниченным, если все его точки лежат внутри некоторого шара. Так, любой отрезок ограниченное множество, прямая неограниченное. Если множество является одновременно ограниченным и замкнутым, то оно называется компактным, или просто компактом.

Далее нам понадобится понятие непрерывной кривой в Em: Пусть функции 'k(t); k = 1; m непрерывны на некотором отрезке [ ; ]: Непрерывной кривой L в пространстве

Em называется множество

2

Будем говорить, что точку A(a1; a2; : : : ; am) можно соединить непрерывной кривой с точкой B(b1; b2; : : : ; bm); если существует такая непрерывная кривая L; определяемая параметризацией (1.1), что

14 апреля 2020 г.

3