Кислицын А.А. Физика атома, атомного ядра и элементарных частиц
37.(2). Теория альфа-распада.
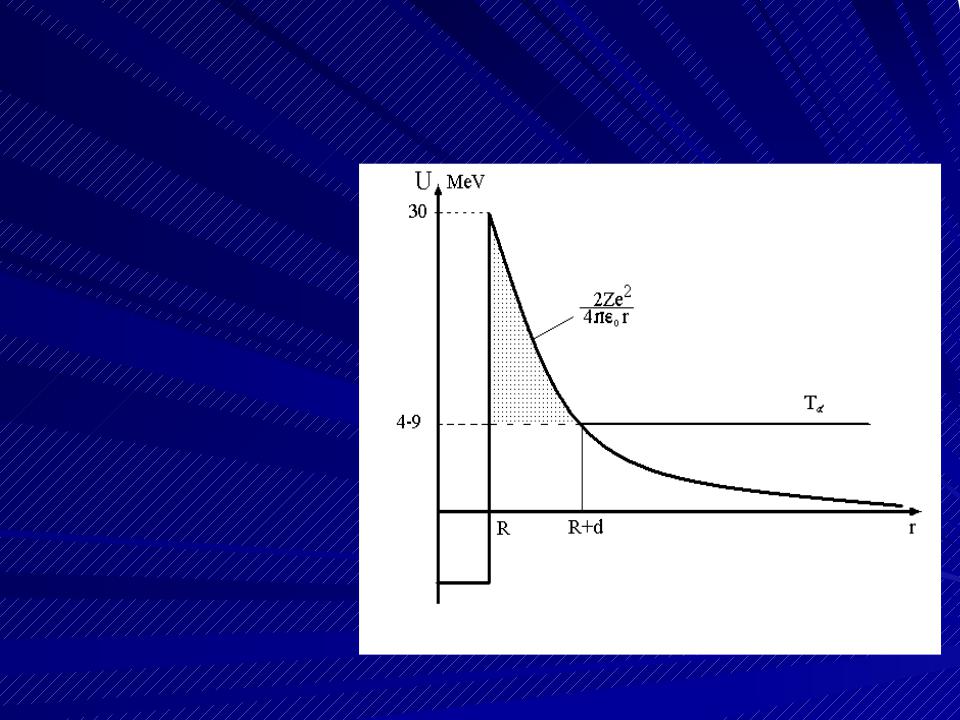
С точки зрения классической физики альфа-распад невозможен
Высота потен-
циального
барьера
больше
кинетичес- кой энергии альфа- частицы.
Альфа-распад - это следствие волновых
свойств микрочастиц, одно из прояв- лений туннельного эффекта.
Туннельным эффектом называется явле-
ние прохождения частицы сквозь потен- циальный барьер; при этом частица не теряет энергию, и выходит из барьера с
той же энергией, с какой в него попа-
дает.
Для барьера прямоугольной формы 
коэффициент прозрачности был най- ден выше (формула (11.22):
D 16E 1 |
|
E |
e |
|
|
|
|
|
|
|
|
2 |
2m(U0 E)d |
U0 |
U0 |
|
|
|
||
Барьер произвольной формы достаточно
представить в виде последовательности
узких прямоугольных барьеров. Тогда
|
|
2 |
d |
|
|
|
|||
D exp |
|
2m U Edx |
||
|
|
0 |
|
|
Применительно к альфа-распаду:
|
2 |
|
R d |
2Ze2 |
|
|
D exp |
|
2m |
|
|
T dr (37.1) |
|
|
4 0r |
|||||
|
|
|
||||
|
R |
|||||
|
|
|
|
|
|
где верхний предел интегрирования R+d находим из условия:
T |
2Ze2 |
|
R d |
2Ze2 |
|
|
4 0 R d |
4 0T |
(37.2) |
||||
|
|
|
||||
|
|
|
|
|
Делаем подстановку
|
r |
|
|
|
2Ze2 |
|
|
|
2Ze2 |
T |
|||||
x R d |
|
|
4 0r |
4 0 |
(R d)x |
x |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dr (R d)dx |
|
2Ze2 |
dx |
|
||||||||||
|
4 |
T |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
пределы интегрирования: |
|
|
|
0 |
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||
|
r R |
|
x |
|
|
R |
|
x |
|
||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
R d |
|
|
0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
r R d |
|
|
x 1 |
|
|
||||||||
Формула (37.1) принимает вид: |
|
|
|
|
|
||||||||||
|
|
2 |
|
2m 2Ze2 |
1 |
|
1 |
|
|
||||||
D exp |
|
|
T |
4 |
|
x |
1 dx |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
0 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
Для вычисления интеграла, учитывая, что 0 x 1 делаем подстановку:
x cos2 y dx 2cos y sin ydy
пределы |
|
|
x 1 |
y 0 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x x |
|
|
cos2 y |
|
|
R |
y |
arccos |
|
R |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
0 |
|
|
|
0 |
|
|
R d |
|
0 |
|
|
|
|
R d |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Вычисляем интеграл: |
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
1 |
|
|
|
0 |
1 |
|
|
|
|
0 |
sin y |
|
|
|
|
|
|||
|
|
1 dx |
2 |
|
|
|
1cos y sin ydy 2 |
|
|
cos y sin ydy |
||||||||||
|
|
2 |
|
|
|
|||||||||||||||
x |
x |
|
|
|
y |
cos |
|
y |
|
|
|
y |
cos y |
|
|
|
|
|
||
0 |
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
2 |
|
|
|
0 |
1 |
|
|
|
1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 sin |
|
ydy 2 |
1 cos 2y dy y |
|
sin 2 y |
|
|
||||||||||||
|
|
y |
|
|
|
|
|
y |
2 |
|
|
|
2 |
|
|
|
|
y |
||
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
y0 |
1 sin 2y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
Итак, |
|
|
2 Ze2 |
|
2m |
|
|
|
||||
D exp |
|
|
|
|
|
|
|
|
2y0 |
sin 2y0 |
||
|
4 |
|
|
T |
||||||||
|
|
|
0 |
|
|
|
|
|
||||
где |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
R |
|
|
|
4 0T R |
||||
y0 |
arccos |
|
arccos |
|||||||||
|
R d |
|
2Ze2 |
|||||||||
Учитывая, что y0 << 1, разлагаем y0 и sin2y0 в ряд и ограничиваемся первыми членами разложения:
y0 arccos |
|
R |
arccos |
4 0T R |
|
4 0T R |
||
|
|
|
2Ze2 |
2 |
|
2Ze2 |
||
|
R d |
|
||||||
|
|
sin 2 y0 2cos y0 sin y0 |
|
|
||||
2 4 0 RT |
1 4 0 RT 2 |
4 0 RT |
|
|||||
|
||||||||
|
2Ze2 |
2Ze2 |
2Ze2 |
|
|
|||
Подставляя указанные разложения, находим:
|
2 |
|
Ze |
2 |
2m |
|
|
|
|
|
|
|
2e |
m RZ |
(37.3) |
||||||
D exp |
|
|
4 |
|
|
|
|
|
||
|
|
0 |
T |
|
|
0 |
|
|
||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Чтобы найти постоянную распада, надо оценить предэкспоненциальный множитель. По физическо- му смыслу рассматриваемой модели, это должна быть частота , с которой альфа-частица, двига- ясь внутри ядра, ударяется о его внутренние стен-
ки: = v/R, где v - средняя скорость альфа-части- цы, которую можно оценить из соотношения неоп- ределенности Rmv . Таким образом: 
|
v |
|
|
(37.4) |
|
R |
mR2 |
||||
|
|
|