Лекции / 7

§ Работа с файлами в Turbo Prolog.

Вначале в разделе domains необходимо определить файловый указатель: domains

file = file_pointer

Затем необходимо сопоставить внешнее имя файла и файловую переменную, установив режим работы с файлом. Это можно сделать с помощью одного из следующих предикатов:

openwrite(file_pointer, file_name), openread(file_pointer, file_name), openmodify(file_pointer, file_name), openappend(file_pointer, file_name).

Предикат openwrite создает новый файл и открывает его для записи. Предикат openread открывает файл для чтения.

Предикат openmodify открывает файл для чтения и записи.

Предикат openappend открывает файл для добавления информации в конец существующего файла.

Для успешного открытия файла необходимо проверить, существует ли он в указанном месте. Для такой проверки можно использовать предикат existfile(file_name). С помощью этого предиката можно расширить стандартные предикаты открытия файлов:

opentoread(F,N):–

existfile(N),!, openread(F,N).

opentoread(_,N):–

write("Файл "N" не найден!").

Данные могут быть выведены в файл, на экран или принтер. Для указания адресата можно использовать предикат writedevice:

writedevice(file_pointer) writedevice(screen) writedevice(printer)

Для считывания данных используется предикат readdevice:

readdevice(file_pointer) readdevice(keyboard)

Для записи используются стандартные предикаты:

write (A1, A2,...);

writef ("формат ", A1,A2,...),

В спецификации формата вывода используется запись типа %m.pf или %-m.pf

Во втором предикате дефис означает выравнивание по левому краю (по умолчанию выполняется выравнивание по правому краю).

m —минимальное число символов.

p — точность представления с плавающей точкой или максимальное число символов.

f — один из спецификаторов формата.

f — вещественное число в представлении с фиксированной точкой ( 123.4) e — вещественное число в экспоненциальном формате ( 1.234e2 )

g — вещественное число в формате f или e (формате по умолчанию) d — символьное или целое число как десятичное число

u — символьное или целое число как беззнаковое целое

x — символьное или целое число как шестнадцатиричное число

1

c — символьное или целое число как набор символов X — длинное шестнадцатиричное число

s — строка ( symbol и string)

В предикатах вывода могут использоваться следующие управляющие символы: \n - переход на новую строку;

\t - табуляция вывода;

\xxx - вывод символа с кодом ххх.

Для считывания данных используются следующие предикаты:

readchar(char),

readint(integer),

readln(string),

readreal(real),

Для завершения работы с открытым файлом используется предикат;

closefile(file_pointer).

§ Работа с окнами в Turbo Prolog.

Для создания окна можно использовать предикат makewindow:

makewindow(window_id, text_back_colors, frame_color, title, start_row, start_column, window height, window_width).

Первый параметр – идентификатор окна.

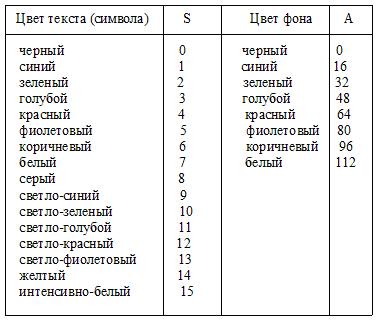
Второй параметр – цвета текста и фона: text_back_colors = S+A, где S - цвет текста, а A - цвет фона:

Вывод символов с мерцанием: text_back_colors = S+A+128. Параметр frame_color — целое число, означающее цвет рамки.

2

Параметр start_row – целочисленный указатель верхней строки окна.

Параметр start_column – целочисленный указатель крайнего левого столбца окна. Параметр window_height –количество строк, занимаемых окном.

Параметр window_width – количество столбцов, занимаемых окном.

Для переключения текущего окна на окно window_id используется предикат shiftwindow(window_id) или gotowindow(window_id). Предикат clearwindow очищает окно, а предикат removewindow удаляет его.

§. Лямбда-исчисление.

Лямбда-исчисление — это механизм, который позволяет формально описать, то есть формализовать любой алгоритм в соответствии с функциональной концепцией. Такая формализация позволяет достаточно просто и естественно описать рекурсию и вложенные среды, а структура формализации позволяет отобразить большинство конструкций, написанных на процедурных языках программирования. В то же время конструкции лямбда-исчисления максимально удобно передаются на функциональных языках. Такие языки, как Haskell, по семантике на 100% соответствуют семантике лямбда-исчисления.

Влямбда-исчислении нет встроенных констант, элементарных операторов, чисел, арифметических операций, условных выражений, циклов и т. п., есть только выражения (функции).

Влямбда-исчислении есть два метода построения выражений. Первый метод называется применением или аппликацией, означает применение функции F к входным данным x и записывается как Fx (без скобок). При этом функцию можно применить саму к себе, то есть возможна запись FF.

Вторым методом является абстракция, в рамках которой функция F(х) записывается как λx.F. Например, λx.x2 представляет собой функцию, возводящую свой аргумент в квадрат. Таким образом, лямбда-абстракция является способом ввода неименованной или анонимной функции. Если x в выражении F(x) не используется, то λx.F выражает собой постоянное значение (константу) со значением F.

3

Использование условных обозначений (нотации) лямбда-исчисления обеспечивает разделение понятий функции f(x) и значения функции в точке x. С помощью лямбда-нотации можно формализовать практически все виды математических выражений. При этом выражения вида λx.λy.F сокращаются до λxy.F (аналогично для большего числа аргументов).

Каррирование позволяет записывать функции нескольких аргументов в обычной лямбда-нотации. Идея заключается в том, чтобы функция сначала применяется только к первому аргументу и результатом такого применения является новая функция от меньшего (на единицу) количества аргументов. Затем новая функция применяется к следующему аргументу и так далее. Например:

(λxy.x + y) 1 2 = (λy.1 + y) 2 = 1 + 2.

Применение или аппликация интерпретируется ассоциативно влево, то есть:

Fxy означает (F(x))(y)

Fxyz означает (((Fx)y)z)

Абстракция интерпретируется ассоциативно вправо, то есть:

λx.xy означает λx.(xy), а не (λx.x)y λxyz.M означает (λx.(λy.(λz.(M))))

Абстракция распространяется вправо настолько далеко, насколько это возможно:

λx.MNK означает λx.(MNK)

Внешние скобки при этом опускаются.

4

Следует понимать, что в каком-либо подвыражении переменная может быть свободной (как в выражении под интегралом), однако во всем выражении она связана какой-либо операцией связывания переменной, такой как операция суммирования. Та часть выражения, которая находится «внутри» операции связывания, называется областью видимости переменной.

В лямбда-исчислении выражения λx.E[x] и λy.E[y] считаются эквивалентными (это называется α- эквивалентностью, и процесс преобразования между такими парами называют α- преобразованием). Разумеется, необходимо наложить условие, что y не является свободной переменной в E[x].

§ Логика лямбда-исчисления.

Таким образом, единственным типом данных лямбда-исчисления являются функции, а для определения одних функций на базе других используются такие две операции, как аппликация Fx и абстракция λx.F(x), при этом выражения λx.F(x) и λy.F(y) означают одну и ту же функцию. Выражения, которые создаются в нотации лямбда-исчисления с помощью операций аппликации и абстракции, называются лямбда-термами. В качестве лямбда-термов могут выступать:

1.Переменная.

2.Константа.

3.Аппликация.

4.Абстракция.

5.Комбинация указанных выше объектов.

При этом комбинации абстракций записываются упрощенным образом:

λx.(λy.yyx) <=> λxy.yyx (yyx называется телом)

Если переменная x находится в теле F λ-абстракции λx.F, то есть является локальной переменной функции (выражения), то она (ее вхождение) называется связанной. Если же она является глобальной, то есть находится во внешней зоне видимости, то называется свободной. Можно сказать, что переменная связана, если она локальна для определенного выражения Примеры:

Связанные переменные можно переименовывать:

λx. x = λy. y = λz. z

λf g x. f (g x) = λu v z. u (v z)

Термы, все переменные которых связаны, называются комбинаторами. Примеры комбинаторов:

I = λx.x

w = λx.(x x)

Ω = ww = λx.(x x) (λx.(x x)) K= λxy.x

K* = λxy.y

S = λfgx. f x (g x)

5

B = λfgx. f (g x)

Термы, которые отличаются друг от друга только именами связанных переменных, считаются - эквивалентными (равнозначными).

Вычисление терма сводится к последовательности его преобразований (операций над функциями), которые называются редукциями. Редукция есть преобразование вида

(λx.M) N → M[x:=N];

M[x:=N] означает результат замены (подстановки) свободных вхождений переменной x в терме M на N (с переименованием связанных переменных во избежание конфликта).

Операция подстановки терма s вместо переменной x в другой терм t обозначается как t[s/x].

Термы называются -эквивалентными в нотации M = N, если M получается из N в результате выполнения определенной последовательности редукций или обратных им преобразований.

Таким образом, в лямбда-исчислении есть две базовые редукции:

-редукция: переименование переменной при подстановке во избежание конфликтов имен;-редукция: подстановка терма в выражение вместо параметра.

Если переменная x не имеет свободных вхождений в теле λx.t x, то это выражение будет эквивалентно t. Соответствующее преобразование (избавление от лишней абстракции) называется η-редукцией.

Редекс ( -редекс) означает применение абстракции к определенному терму и имеет вид (λx.M)N.

Нормальная ( -нормальная) форма лямбда-терма не содержит ни одного -редекса.

Пример нормальной формы терма

λxy.x (λz.zx) y

Вместе с тем есть термы, у которых нет нормальной формы, например, (λx.x x) (λy.y y).

(λx.x x) (λy.y y) = (λy.y y) (λy.y y) = (λy.y y) (λz.z z) = (λz.z z) (λz.z z) = …

Не все последовательности редукций приводят к нормальной форме, если она есть. Неправильно подобранная последовательность редукций может привести к неправильному результату. Например, если начать редукцию выражения (λх.у) ((λх.х х х) (λх.х х х)) с самого внутреннего редекса, то получим бесконечную последовательность редукций:

(λх.у) ((λх.х х х) (λх.х х х))

→(λх.у) ((λх.х х х) (λх.х х х) (λх.х х х))

→(λх.у) ((λх.х х х) (λх.х х х) (λх.х х х) (λх.х х х))

Если начать с самого левого и самого внешнего редекса, то сразу получается y и терм приводится к нормальной форме.

Теорема 1. Если S приводится к Т, где Т находится в нормальной форме, то последовательность редукций, начинающаяся с S, построенная таким образом, чтобы для редукции всегда выбирался самый левый и самый внешний редекс, гарантированно завершится и приведет терм в нормальную форму.

Теорема 2. Если t приводится к s1 и t приводится к s2 , то существует терм u, такой, что s1 приводится к u и s2 приводится к u.

Теорема 2 имеет два важных следствия.

Следствие 1. Если t1 = t2, то существует терм u такой, что t1 приводится к u и t2 приводится к u.

6

Следствие 2. Если t = t1 и t = t2 , где t1 и t2 находятся в нормальной форме, то t1 ≡ t2 , т.е. t1 и t2 равны с точностью до переименования переменных.

Следовательно, нормальная форма, если она существует, единственна с точностью до α-

редукции. Иначе говоря, если к терму невозможно применить никакие преобразования, кроме - редукции, этот терм выражен в нормальной форме.

Способ редукции λ-терма, при котором на каждом шаге редукции выбирается самый левый и самый внешний β-редекс, называется нормальной редукционной стратегией.

MN => сначала редуцируем M, потом N

(λx.M)N => сначала M[x/N], потом М и N

η-редукции выполняются после всех β-редукций

Аппликативная редукционная стратегия – способ редукции λ-терма, при котором на каждом шаге редукции выбирается β-редекс, не содержащий других β-редексов

АРС работает быстрее за счёт того, что каждый β-редекс редуцируется только один раз и не дублируется:

Пример: (λx.xx)((λxy.x) 1 0)

АРС: → (λx.xx)(1) → 11

НРС: → ((λxy.x) 1 0)((λxy.x) 1 0) → (1)((λxy.x) 1 0) → 11

НРС гарантирует получение нормальной формы, если нормальная форма существует

7