
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное автономное образовательное предприятие высшего профессионального образования
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ
___________________________________________________________________________________
В.И.Устимов, В.Г.Фарафонов
ОСНОВЫ КОРРЕЛЯЦИОННОГО И РЕГРЕССИОННОГО АНАЛИЗА
Учебное пособие
ГУАП
Санкт-Петербург
2014
1
АННОТАЦИЯ
Учебное пособие составлено в соответствии с программой по высшей математике для студентов экономических специальностей.
В пособии рассмотрены разделы курса теории вероятностей и математической статистики: основы корреляционного и регрессионного анализа. Каждый раздел содержит теоретические сведения и формулы, проиллюстрированные подробно разобранными примерами. Завершают пособие 10 вариантов контрольных работ для заочников, каждый из которых содержит 4 задачи.
Настоящее пособие может быть рекомендовано как студентам бакалавриата, так и магистратуры, углублённо изучающим вопросы теории вероятностей и математической статистики.
2
ВВЕДЕНИЕ
Математико-статистические исследования становятся необходимым инструментом для получения более глубоких и полноценных знаний о механизме случайных явлений и процессов. Овладение приемами статистической обработки наблюдений, освоение методов составления уравнений, дающих адекватное описание изучаемого явления, — непременное условие получения корректных выводов.
Внастоящем пособии, на примере двух случайных величин, рассматриваются корреляционный и регрессионный анализ, широко применяемые при построении математических моделей. Данные методы обработки и анализа статистических данных широко распространены в экономике и социальных науках (в частности в психологии и социологии), контроле качества промышленной продукции, металловедении, агрохимии, гидробиологии, биометрии и т.п., что обусловлено простотой подсчёта коэффициентов корреляции и регрессии и тем, что их применение не требует специальной математической подготовки.
Пособие состоит из двух разделов. В первом разделе (Главе 1), рассматривается построение корреляционного поля, корреляционных таблиц и вычисление выборочного корреляционного коэффициента. Там же достаточно подробно описана процедура построения доверительного интервала для коэффициента корреляции и определения значимости корреляционной связи. Во втором разделе (Главе 2) обсуждается построение кривых регрессии, в том числе и построение линейной регрессии.
Авторы стремились изложить материал , с одной стороны, наиболее просто и понятно,
сдругой стороны - достаточно строго с математической точки зрения. Применяемый математический аппарат основан на программе начального университетского курса высшей математики, в частности теории вероятностей и математической статистики.
Впособии приведены экономические примеры, которые позволяют наглядно продемонстрировать последовательность обработки данных. При этом следует отметить, что примеры будут понятны не только студентам экономических специальностей, но и студентам, обучающимся по техническим направлениям и информатике.
Пособие завершается 10 вариантами контрольных работ, что позволяет использовать его при заочной форме обучения. Каждая контрольная содержит 4 задачи, связанных с обработкой данных методами корреляционного и регрессионного анализа.
Санкт-Петербург, |
В.И.Устимов |
сентябрь 2014 г. |
В.Г. Фарафонов |
3
ГЛАВА 1. ОСНОВЫ КОРРЕЛЯЦИОННОГО АНАЛИЗА
Корреляция (от лат. correlatio — соотношение, взаимосвязь), корреляционная зави-
симость — статистическая взаимосвязь двух или нескольких случайных величин. При этом изменения значений одной или нескольких из этих величин приводит к систематическому изменению значений другой или других величин.
Зависимость между тремя и бóльшим числом случайных величин изучается методами
многофакторного корреляционного анализа [ 5-6 ], которые сводятся к вычислению ча-
стных и множественных коэффициентов корреляции и корреляционных отношений.
В настоящем пособии мы ограничимся рассмотрением взаимосвязью двух случайных величин ξ и η, математической мерой корреляции которых является коэффициент кор-
реляции rξη.
Корреляционный анализ – это совокупность основанных на теории математической статистики (теории корреляции) методов обнаружения корреляционной зависимости между случайными величинами.
Для двух случайных величин ξ и η корреляционный анализ состоит из следующих этапов:
-построение корреляционного поля и составление корреляционной таблицы;
-вычисление выборочного коэффициента корреляци;
-проверка статической гипотезы о значимости корреляционной связи. Рассмотрим подробнее каждый из указанных этапов.
1.1. Корреляционное поле и корреляционная таблица.
Корреляционное поле и корреляционная таблица являются исходными данными при корреляционном анализе. Пусть (xi, xj) - значения, которые принимают соответственно случайные величины ξ и η в процессе парных измерений (i = 1, ..., n; j = 1, ..., n). Изображая полученные результаты в виде точек в декартовой системе координат, получим корреляционное поле. По характеру расположения точек поля можно составить предварительное представление о форме зависимости случайных величин, например, о том, что одна из них в среднем возрастает (рис. 1a) или убывает (рис. 1b) с возрастанием другой.
yi |
yi |
xi |
xi |
Рис. 1a |
Рис. 1b |
4

Пример 1. По 30 фитнес-центрам были установлены затраты ξ на рекламу и количество реализованных годовых абонементов η. В таблице фирмы ранжированы по величине затрат на рекламу:
Таблица 1. Статистические данные (выборка) для примера 1.
|
Затраты на |
Количество |
|
Затраты на |
Количество |
№ n/n |
рекламу, |
реализован. |
№ n/n |
рекламу, |
реализован. |
|
тыс. руб. |
абонементов |
|
тыс. руб. |
абонементов |
1 |
160 |
800 |
16 |
215 |
1150 |
2 |
170 |
730 |
17 |
220 |
1000 |
3 |
170 |
800 |
18 |
220 |
1200 |
4 |
175 |
850 |
19 |
220 |
1250 |
5 |
180 |
800 |
20 |
220 |
1300 |
6 |
180 |
880 |
21 |
225 |
1250 |
7 |
180 |
950 |
22 |
230 |
1300 |
8 |
185 |
820 |
23 |
230 |
1350 |
9 |
190 |
900 |
24 |
235 |
1400 |
10 |
190 |
1000 |
25 |
235 |
1450 |
11 |
195 |
920 |
26 |
240 |
1500 |
12 |
200 |
1060 |
27 |
240 |
1600 |
13 |
205 |
950 |
28 |
250 |
1550 |
14 |
210 |
900 |
29 |
260 |
1700 |
15 |
210 |
1200 |
30 |
270 |
1700 |
Корреляционное поле, построенное по статистическим данным, приведено на рис. 2. |
|||||||
|
|
Рис. 2. |
Корреляционное поле |
|
|
||
Количество реализованных абонентов |
1800 |
|
|
|
|
|
|
1600 |
|
|
|
|
|
|
|
1400 |
|
|
|
|
|
|
|
1200 |
|
|
|
|
|
|
|
1000 |
|
|
|
|
|
|
|
800 |
|
|
|
|
|
|
|
600 |
|
|
|
|
|
|
|
400 |
|
|
|
|
|
|
|
200 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
50 |
100 |
150 |
200 |
250 |
300 |
|
|
|
Затраты на рекламу, тыс.руб |
|
|
||
Анализ рис. 2. позволяет сделать вывод о наличии сильной линейной статистической |
|||||||
связи между затратами фитнес-центров на рекламу и количеством реализованных годо- |
|||||||
5
вых абонементов. При этом связь имеет положительную тенденцию, то есть с ростом переменной ξ наблюдается увеличение величины η.
В случае наличия большого числа различных значений результативного признака (в нашем случае величины η), соответствующих одному и тому же значению признакафактора (величины ξ), целесообразнее воспользоваться для установления факта наличия связи корреляционной таблицей.
Построение корреляционной таблицы начинают с группировки значений факторного и результативного признаков. Для результативного признака необходимо определить величину интервала группировки ∆l . Это можно сделать с помощью формулы Стержэсса, в которой n=30:
l |
|
|
ymax ymin |
|
1700 730 |
161. |
(1.1) |
|
1 |
3,322lgn |
6 |
||||||
|
|
|
|
|||||
Таблица 2. Корреляционная таблица (выборочный закон распределения) для примера 1.
[li, li+1] |
[730;891] |
[892;1053] |
[1054;1215] |
[1216;1377] |
[1378;1539] |
[1540;1701] |
l \ k |
810,5 |
972,5 |
1134,5 |
1296,5 |
1458,5 |
1620,5 |
160 |
1 |
0 |
0 |
0 |
0 |
0 |
170 |
2 |
0 |
0 |
0 |
0 |
0 |
175 |
1 |
0 |
0 |
0 |
0 |
0 |
180 |
2 |
1 |
0 |
0 |
0 |
0 |
185 |
1 |
0 |
0 |
0 |
0 |
0 |
190 |
0 |
2 |
0 |
0 |
0 |
0 |
195 |
0 |
1 |
0 |
0 |
0 |
0 |
200 |
0 |
0 |
1 |
0 |
0 |
0 |
205 |
0 |
1 |
0 |
0 |
0 |
0 |
210 |
0 |
1 |
1 |
0 |
0 |
0 |
215 |
0 |
0 |
1 |
0 |
0 |
0 |
220 |
0 |
1 |
1 |
2 |
0 |
0 |
225 |
0 |
0 |
0 |
1 |
0 |
0 |
230 |
0 |
0 |
0 |
2 |
0 |
0 |
235 |
0 |
0 |
0 |
0 |
2 |
0 |
240 |
0 |
0 |
0 |
0 |
1 |
1 |
250 |
0 |
0 |
0 |
0 |
0 |
1 |
260 |
0 |
0 |
0 |
0 |
0 |
1 |
270 |
0 |
0 |
0 |
0 |
0 |
1 |
В корреляционной таблице факторный признак ξ, как правило, располагают в строках, а результативный признак η – в столбцах таблицы. Здесь k = (lk + lk+1 )/2, k = 1, ..., n(k) и l = 1, ..., n(l). Числа nlk, расположенные на пересечении строк и столбцов таблицы, означают частоту повторения данного значения ξ и η. Для nlk, справедливо соотношение:
n(l)n(k )
nlk =n. (1.2)
l 1 k 1
6
Если в табл. 2 разделить частоты nlk на n, то мы получим выборочный закон распределения. Числа, расположенные на пересечении строк и столбцов таблицы, являются относительными частотами, которые представляют собой выборочные вероятности
nlk/ / n (здесь и дальше будет относиться к величинам, рассчитываемым по выборке).
Данная корреляционная таблица уже при общем знакомстве дает возможность выдвинуть предположение о наличии или отсутствии корреляции, а также выяснить ее направление. Так как в нашем случае частоты расположены на диагонали из левого нижнего угла в правый верхний угол (т.е. бóльшим значениям фактора соответствуют бóльшие значения функции), то можно предположить наличие прямой корреляционной зависимости между признаками.
1.2. Выборочный коэффициент корреляции.
Для начала вспомним, как определяется и какие свойства имеет теоретиковероятностный коэффициент корреляции.
Случайная величина в основном хорошо описывается двумя числовыми характеристиками: математическим ожиданием и дисперсией. Чтобы описать систему из двух случайных величин кроме «основных» характеристик используют так же корреляционный момент и коэффициент корреляции.
Корреляционным моментом (ковариацией) Kξη [ 1 ] называется математическое ожидание произведения центрированных случайных величин ξ и η и характеризует степень линейной статистической зависимости величин ξ и η и рассеивание относительно точки (mξ , mη).
|
|
M |
|
|
|
|
|
|
|
|
|
m M ξ |
|
|
|
|
|
|
K |
|
|
- m |
|
|
η - m |
|
, |
где |
и |
m M |
|
|
(1.3) |
||||
|
|
|
|
ξ |
|
|
η |
|
|
|
|
|
|
|
|
|
||
или
K |
|
M - mξ - mη |
M - mη - mξ |
|
|
|
|
|
|
m m M m m .
Свойства корреляционного момента:
1.- ∞ < Kξη < ∞;
+ m |
m |
M |
|
M m |
M m |
|
||
ξ |
η |
|
|
|
η |
|
ξ |
(1.4) |
|
|
|
|
|
|
|
|
|
2. |
Kξη = Kηξ . Свойство 2 следует из определения Kξη . |
3. |
Корреляционный момент двух независимых случайных величин ξ и η равен 0. |
|
Доказательство: так как случайные величины ξ и η – независимы, то и их совмест- |
ная плотность распределения представляется произведением плотностей распределения отдельных случайных величин ξ и η.
Тогда |
M M M и |
K |
|
M m m |
m m |
m m 0. |
|
|
|
|
|
|
7
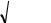
4. Абсолютная величина корреляционного момента двух случайных величин не превышает среднего геометрического их дисперсий:
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
K |
|
|
или |
|
K |
|
D D |
(1.5) |
|||
|
|
|
|
|
|
|
|
|
||||
|
|
Доказательство: |
Введем в рассмотрение случайные величины z1=σηξ - σξη и |
|||||||||
z2=σηξ + σξη. Вычислим их дисперсии D[z1] |
и D[z2]. |
|||||||||||
Из того, что D[z1] ≥ 0, получим:
D z M
1
2 M
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
z |
2 |
M |
z |
|
|
|
M |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
2 |
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
2 |
|
2 |
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|
|||||||||
|
|
|
|
M |
|
|
|
|
|
|
M |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
2 |
|
|
|
K |
|
|
|
0. |
|
|
|||||||
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
В результате: Kξη ≤ σξση. |
|
Аналогично, из неравенства |
D[z2] ≥ 0 нетрудно показать, что - σξση ≤ Kξη . |
Отсюда - σξση ≤ Kξη ≤ σξση |
и |Kξη| ≤ σξση . |
Если Kξη ≠ 0, случайные величины ξ и η называются коррелированными (зависимыми в определённом смысле). Если же Kξη = 0, то необязательно, что ξ и η независимы. В этом случае они называются некоррелированными. Итак, из коррелированности двух случайных величин следует их зависимость, но из зависимости еще не вытекает их коррелированность.
Из независимости двух случайных величин следует их некоррелирванность, но из некоррелированности еще нельзя заключить о независимости этих величин.
Величина ковариации (корреляционного момента) даёт нам лишь качественную характеристику корреляции. Корреляционный момент зависит от единиц измерения случайных величин, входящих в систему, и от того, насколько каждая из случайных величин отклоняется от своего математического ожидания. Для количественной оценки связи между ξ и η удобно рассматривать безразмерную характеристику корреляции, которая назы-
вается коэффициентом корреляции rξη:
r |
K |
. |
|
|||
|
|
|||||
|
|
|
|
|
|
|
|
(1.6) |
|||||
|
|
|
||||
|
|
|
|
|
|
|
Свойства коэффициента корреляции:
1. Величина коэффициента корреляции двух случайных величин не превышает единицы: |Kξη |≤1. Это утверждение прямо следует из доказанного выше неравенства |Kξη| ≤ σξση . (1.5) и определения коэффициента корреляции (1.6).
2. |rξη |=1, если η=a+bξ.
Доказательство: Используя свойства математического ожидания, получим:
8
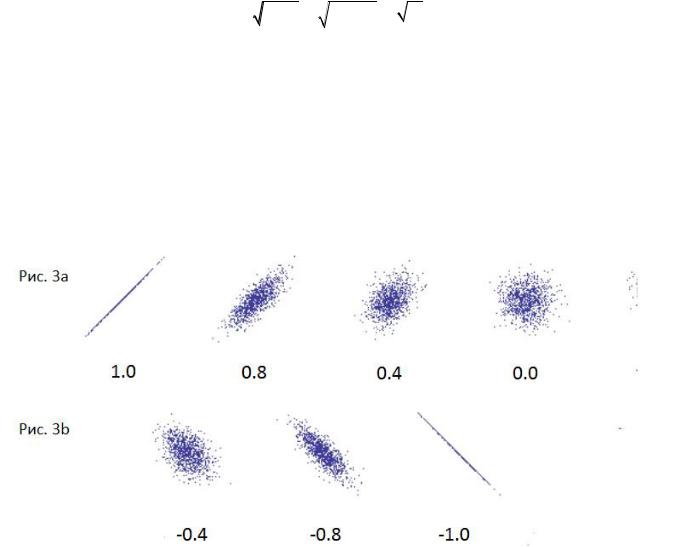
K M M |
M |
M a b ) M M a b aM bM 2 |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
aM |
bM |
2 |
b M 2 |
M |
2 |
b 2 bD . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Найдём дисперсию η: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
D M |
2 |
|
M 2 M a b )2 |
M |
a b M |
a b |
a2 |
b2M 2 |
|
2abM |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
2 |
b |
2 |
M |
2 |
|
|
|
|
b |
2 |
|
|
2 |
M |
2 |
2 |
|
2 |
b |
2 |
D . |
|
|
|
|
|
|
|
||||||||
|
|
|
2abM |
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Подставим выражения для Kξη |
|
и Dη в (1.6):: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
Kξη |
|
|
|
|
bDξ |
|
|
|
|
b |
|
b |
. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
ξη |
|
|
Dξ Dη |
b2 D D |
|
|
b2 |
|
b |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ξ |
|
ξ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, |
rξη = 1, |
если b>0 |
и rξη = -1, если |
b<0. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Коэффициент корреляции служит для оценки тесноты линейной связи между ξ и η: чем ближе абсолютная величина коэффициента корреляции к 1, тем связь сильнее, чем ближе к 0, тем слабее.
3. Если величины ξ и η независимы, то rξη= 0.
4. На рис.3a, 3b схематично показано, как меняется коэффициент корреляции от +1 до 1 в зависимости от вида корреляционного поля:
Как мы уже отмечали, для независимых случайных величин коэффициент корреляции равен нулю, обратное неверно и требуются дополнительные исследования.
На рис. 3c, 3d представлены примеры, когда несмотря на то, что rξη= 0, на корреляци-
онном поле можно увидеть зависимость между случайными величинами.
9

Выборочный коэффициента корреляции.
Выборочный коэффициента корреляции находится по статистическим данным (выборке) или корреляционной таблицей, используя формулы (1.7) - (1.10) (здесь используются обозначения как в табл.1 и табл. 2):
|
|
|
|
|
|
|
|
r |
|
|
K |
|
, |
|
|
|||
|
|
|
|
|
|
|
|
|
ξη |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
ξη |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D D |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
ξ |
η |
|
|
|
|
|
|
1 |
n n |
|
|
|
|
|
1 |
n n |
|
|
1 |
n(l)n(k ) |
||||
Kξη |
(xi x)( y j y) |
xi y j xy |
xl yk nlk xy, |
|||||||||||||||
|
|
|
|
|
||||||||||||||
|
|
n i 1 j 1 |
|
|
|
|
|
n i 1 j 1 |
|
n l 1 k 1 |
||||||||
|
|
|
n |
|
|
|
|
n |
|
|
|
|
n(l) |
|
|
|
||
D |
1 xi |
x 2 |
1 xi2 x2 1 xl 2nl x2 , |
|
|
|||||||||||||
|
n i 1 |
|
|
|
n i 1 |
|
|
|
|
n l |
1 |
|
|
|
||||
|
|
|
n |
|
y 2 |
|
|
n |
|
|
|
|
|
n(k ) |
|
|
||
D |
1 y j |
|
1 y j 2 y 2 1 |
yk 2nk y 2 , |
||||||||||||||
|
n j 1 |
|
|
|
|
n j 1 |
|
|
|
|
n k 1 |
|
|
|||||
где и - выборочные средние:
(1.7)
(1.8)
(1.9)
(1.10)
|
n |
n(k ) |
|
n |
|
n(l) |
|
n(l) |
n(k ) |
x |
1 xi |
1 xk nk , |
y |
1 y j |
|
1 yl nl |
и nk nlk , |
nl nlk . |
|
|
n i 1 |
n k 1 |
|
n j 1 |
|
n l 1 |
|
l 1 |
k 1 |
Выборочный коэффициент корреляции rξη = 0 |
обладает всем свойствами, которыми |
||||||||
обладает теоретико-вероятностный коэффициент корреляции rξη . В частности, для лю-
бой выборки: |rξη| ≤ 1. При этом, чем ближе |
rξη к 1 (или к 1), тем сильнее выражена |
линейная зависимость между ξ и η. |
|
|
10 |
