
Найдём выборочные средние, дисперсии и корреляционный коэффициент для примера 1, рассмотренного выше.
Расчёты будем проводить двумя способами. В первом случае мы воспользуемся статистическими данными (выборкой), приведёнными в табл.1. Второй вариант расчёта будет основан на корреляционной таблице (табл.2), которую для удобства представим в более удобном для вычисления виде, соответствующем выборочному закону распределения (табл.3). Результаты вычислений приведены в табл.4
Таблица 3 Выборочный закон распределения для примера 1.
l \ k |
810,5 |
972,5 |
1134,5 |
1296,5 |
1458,5 |
1620,5 |
nl |
160 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
170 |
2 |
0 |
0 |
0 |
0 |
0 |
2 |
175 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
180 |
2 |
1 |
0 |
0 |
0 |
0 |
3 |
185 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
190 |
0 |
2 |
0 |
0 |
0 |
0 |
2 |
195 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
200 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
205 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
210 |
0 |
1 |
1 |
0 |
0 |
0 |
2 |
215 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
220 |
0 |
1 |
1 |
2 |
0 |
0 |
4 |
225 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
230 |
0 |
0 |
0 |
2 |
0 |
0 |
2 |
235 |
0 |
0 |
0 |
0 |
2 |
0 |
2 |
240 |
0 |
0 |
0 |
0 |
1 |
1 |
2 |
250 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
260 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
270 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
nk |
7 |
7 |
4 |
5 |
3 |
4 |
30 |
Таблица 4 |
Выборочные средние, дисперсии и корреляционный. коэффициент . . |
||||||||
|
|
|
|
|
|
|
|
|
|
Варианты |
|
|
|
|
|
|
Dξ |
Dη |
rξη |
|
|
|
|
|
|
||||
расчётов |
|
|
|
|
|
|
|
|
|
1 |
210.3 |
1142.0 |
786.6 |
82576 |
0.9485 |
||||
2 |
210.3 |
1145.3 |
786.6 |
76866 |
0.9406 |
||||
Более точным следует признать первый вариант расчёта. Второй вариант вычислений связан с предварительной группировкой статистических данных. Результаты расчётов естественно зависят от выбранного способа группировки. Это объясняет некоторые отличия выборочных моментов, полученных по второму варианту расчёта, от их точных значений для данной выборки.
Однако, следует отметить, что в рассмотренном примере отличия оказываются незначительными. Так корреляционный коэффициент, вычисленный по второму варианту расчёта (0.9406), меньше точного значения (0.9485) всего на 0.8%.
11

1.3. Проверка статической гипотезы о значимости корреляционной связи.
Мало найти коэффициент корреляции, необходимо подкрепить значимость соответствующей зависимости путём проверки статистической гипотезы.
Проверка гипотезы о наличии корреляции осуществляется следующим образом. Основная гипотеза – отсутствие линейной статистической связи H0: rξη =0, альтернативной гипотезой может выступать любая из трех возможных:
rξη 0
H1 : rξη 0,
rξη 0
В тех случаях, когда справедливо предположение о нормальном распределении выборки, в качестве статистического критерия выберем случайную величину
|
r |
|
|
|
|
|
|
n 2 |
|
|
|||
Z |
η |
|
|
, |
(1.11) |
|
|
|
|
|
|||
1 r 2 |
||||||
|
|
|
ξη |
|
|
|
где rξη - выборочный коэффициент корреляции, |
n - объем выборки. |
|
||||
Случайная величина Z имеет распределение Стьюдента [ 2 ] c n-2 степенями свободы
St(n-2).
Пусть α - уровень значимости, который равен вероятности ошибочного отклонения (отвержения) гипотезы H0: rξη =0, в то время как она на самом деле верна.
Рассмотрим в качестве примера альтернативную гипотезу H1: rξη ≠0. В этом случае критическая область, удовлетворяющая условию p(|Z|>Zα)=α, является двусторонней, поскольку состоит из двух частей Z< -Zα и Z> +Zα (рис. 4).
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
fSt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S = 1 -α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Критическая область |
|
|
|
|
2 |
|
|
|
|
|
|
|
Критическая область |
|
|
|
|||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
S =α/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S =α/2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-25 |
-20 |
-15 |
-10-Zα |
-5 |
|
0 |
5 |
Zα10 |
15 |
20 |
25 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4
12

Вероятность попадания критерия Z в каждую из половин критической области равна α/2. Поэтому Zα определяется из соотношения p(Z>Zα)=α/2. Вычислим Z, подставив в формулу (1.11) найденное для исследуемой выборки значение выборочного коэффициента корреляции rξη. Нулевую гипотезу H0 можно принять, если |Z|< Zα, и следует отвергнуть в случае |Z| > Zα.
Если альтернативная гипотеза H1: rξη >0, то критическая область удовлетворяет условию p(Z>Zα)=α и является правосторонней Z> +Zα (рис. 5).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
fSt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S = 1 -α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
Критическая область |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S =α |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-25 |
-20 |
-15 |
-10 |
-5 |
|
0 |
5 |
Zα10 |
15 |
20 |
25 |
||||||||||||||||||||
Рис. 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Величина Zα |
определяется из соотношения p(Z>Zα)=α.. Нулевую гипотезу H0 прини- |
||||||||||||||||||||||||||||
мают, если Z < |
Zα, |
и отвергают в противоположном случае Z > Zα |
[ 2 ]. |
|
|
|
|
|
|||||||||||||||||||||||
Проиллюстрируем вышесказанное на нашем примере 1. Выберем уровень значимости α = 0.01. Сначала рассмотрим двустороннюю критическую область. Значение Zα можно найти либо из таблицы критических точек для распределения Стьюдента с 28 степенями свободы (p(Z>Zα) = 0.005), либо из таблицы квантилей распределения Стьюдента (p(Z<Zα) = 0.995). В результате получим (см., например, таблицу 2 из ПРИЛОЖЕНИЯ):
Z t ,n t ,28 t ,28 2.7633.
Для правосторонней критической области величина Zα находится из условия p(Z>Zα) = 0.01 (по таблице критических точек) или из соотношения p(Z<Zα) = 0.99 (по таблице квантилей).
Врезультате для правосторонней критической области Zα = t 0.99, 28 = 2.4671.
Впримере 1 выборочный корреляционный коэффициент, вычисленный первым ( более точным) способом, равен 0,9485, тогда
|
|
|
|
|
|
|
|
|
Z |
0.9485 28 2 |
|
4.8364 |
15.27. |
||||
|
|
|
0.3168 |
|||||
1 0.94852 |
||||||||
|
|
|
||||||
13

В результате, т.к. Z >> Zα (15.27 >> 2.7633 в случае двусторонней критической области и 15.27 >> 2.4671 для односторонней критической обрасти), можно сделать вывод, что в нашем случае гипотезу об отсутствии линейной зависимости между случайными ве-
личинами ξ и η следует отбросить и корреляционная связь является значимой.
Отметим, что при объёмах выборки n>30 квантили распределения Стьюдента
tγ,n (тут p(t <tγ,n) = γ, где n - число степеней свободы) можно находить по приближённой формуле, используя квантили нормального распределения Uγ:
t ,n |
|
Uγ |
|
|
. |
(1.12) |
||
|
|
|
|
|
||||
1 (1/ 4n))2 |
(Uγ )2 |
/ 2n |
||||||
|
|
|
|
|||||
Преобразование Фишера
Статистика Стьюдента не позволяет получить надёжных выводов о значимости корреляционных зависимостей в случае малых значений выборочного корреляционного коэффициента и относительно небольших выборках. Менее чувствительной к объему выборки является статистика, основанная на преобразовании Фишера:
|
1 |
|
1 r |
|
|
V |
ln |
ξη |
(1.13) |
||
|
|
. |
|||
2 |
1 r |
||||
|
|
|
ξη |
|
|
Фишером было показано, что при n ≥30 случайная величина V имеет приближенно нормальное распределение с независящей от rξη дисперсией
|
σ2 |
1 |
|
|
|
|||
|
|
|
|
|
|
|
||
|
|
n 3 |
|
|||||
|
|
V |
|
|
||||
|
|
|
|
|
|
|
|
|
и математическим ожиданием |
|
|
|
|
|
|
|
|
m 1 ln1 ρ |
|
ρ |
, |
|||||
|
|
|||||||
V |
2 |
1 ρ |
2n 2 |
|
||||
|
|
|||||||
lim m |
1 ln1 ρ , |
(1.14) |
||||||
n |
V |
2 |
|
|
1 ρ |
|
||
|
|
|
|
|||||
|
|
|
, |
|
|
|
||
где ρ – истинное (но неизвестное) значение коэффициента корреляции rξη . |
||||||||
Величина |
V mV |
|
|
|
|
|
|
|
U |
|
|
N (0,1), |
(1.15) |
||||
|
|
|
||||||
|
|
σV |
|
|
|
|
|
|
где N(0,1) - нормальное распределение с нулевым математическим ожиданием и единичной дисперсией.
Заметим, что с помощью указанной статистики можно проверять более общую гипотезу о сравнении с эталоном H0:ρ = ρ0 при любой из трёх альтернативных гипотез
14

|
ρ0 |
|
|
|
|
|
|
H : ρ |
0 |
. |
|
1 |
|
|
|
|
ρ0 |
|
|
В этом случае mV заменяется на условное математическое ожидание
|
|
|
1 |
ln |
|
1 ρ0 |
|
|
|
||||||
M V | H0 |
|
2 |
1 |
ρ0 |
|||
|
|
|
|
||||
и центрирование статистики V в формуле (1.15) осуществляется на эту величину.
Возвращаясь к нашему примеру 1, проверим значимость найденного выборочного коэффициента корреляции. Тогда основная гипотеза H0:ρ = 0 – отсутствие линейной статистической связи, условное математическое ожидание M[V|H0]=0 и
|
|
|
|
1 rξη |
|
U |
|
n 3 |
|
||
|
|
ln |
|
: N (0,1). |
|
|
2 |
1 r |
|||
|
|
|
|
ξη |
|
Вычислим U , полагая rξη = 0.9485 и n = 30,
U 
 30 3 ln 1 0, 9485 2.5981ln(37.8350) 9.4395. .
30 3 ln 1 0, 9485 2.5981ln(37.8350) 9.4395. .
2 1 0, 9485
Критические точки Uα находим для уровня значимости α = 0.01 из таблицы квантилей нормального распределения: (например, используя функции Лапласа Φ0(x) из таблицы 1 ПРИЛОЖЕНИЯ: Φ0(Uα) = 0.5 - α для односторонней области и Φ0(Uα) = 0.5 - α/2 для двусторонней. В первом случае Uα = 2.32 , во втором - Uα = 2.58. В обоих случаях U попадает в критическую область (U >Uα), гипотезу об отсутствии линейной статистической связи следует отбросить. Вероятностью ошибки при этом равна α = 0.01.
1.4. Доверительный интервал для корреляционного коэффициента.
Воспользовавшись преобразованием Фишера (1.13) и соотношением (1.15), можно построить доверительный интервал для выборочного коэффициента корреляции.
Действительно,
|
1 |
|
1 r |
|
V |
ln |
ξη |
, |
|
2 |
1 r |
|||
|
|
|
ξη |
|
V = arcth(rξη) - гиперболический арктангенс, возрастающая нечётная функция:
V(-rξη) = -V(rξη).
Распределение вероятностей значений V приближается (тем более точно, чем больше объём выборки n) нормальным распределением N(mV,σV) с параметрами
15
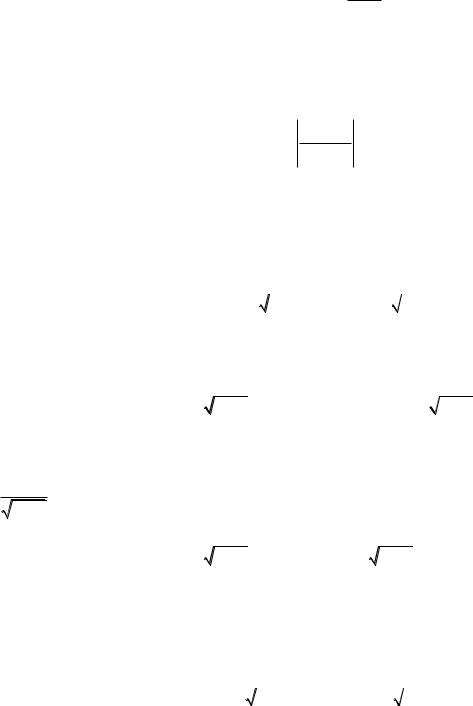
m |
1 |
ln1 |
ρ |
ρ |
(1.16) |
|
|
||||
V |
2 |
1 |
ρ |
2n 2 |
|
|
|
и V2 n 1 3.
Статистика случайной величины U = (V - mV)/σV имеет асимптотическое стандартное нормальное распределение N(0,1). Доверительный интервал для нормального отклонения с надёжностью (доверительной вероятностью) γ определяется неравенством:
VmV U ,V
где Uγ - квантиль уровня (1+γ)/2 распределения N(0,1), т.е. Uγ - корень уравнения
Φ0(Uγ) = γ/2 (Φ0(x) - функция Лапласа).
Доверительный интервал для математического ожидания mV :
|
|
V |
|
Uγ |
|
|
mV |
V |
Uγ |
|
|
|
. |
|
|
(1.17) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
n |
3 |
|
n |
3 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Подставляя в (1.17) выражение для mV (1.16) получим: |
|
|
|
|
|
|
|
|
||||||||||||||||
V |
Uγ |
|
|
1 |
ln |
1 ρ |
|
ρ |
|
V |
|
|
|
Uγ |
|
. |
(1.18) |
|||||||
|
|
|
|
|
1 ρ |
2n 2 |
|
|
|
|
|
|
||||||||||||
|
n 3 |
2 |
|
|
|
|
n 3 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Величиной ρ/(2n-2) в выражении для mV (1.16) можно пренебречь, принимая во внимание, что при n → ∞ она есть бесконечно малая более высокого порядка в сравнении с
Uγ |
: |
n 3 |
V |
Uγ |
|
|
1 |
ln |
1 ρ |
V |
Uγ |
|
. |
(1.19) |
||
|
|
|
|
1 ρ |
|
|
|
||||||
|
n 3 |
2 |
|
n 3 |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||
Решение относительно ρ данного двойного неравенства (1.19) приводит к искомому
доверительному интервалу для коэффициента корреляции (th(x)) - гиперболический тангенс) :
|
Uγ |
|
|
|
Uγ |
|
|
|
||
th V |
|
|
|
|
th V |
|
|
|
. |
(1.20) |
|
|
|
|
|
|
|||||
|
n 3 |
|
n 3 |
|||||||
|
|
|
|
|
|
|
|
|
||
Этапы определения доверительного интервала для коэффициента корреляции рассмотрим на примере 1.
Выберем доверитель вероятность (надёжность) γ = 0.90 , тогда Φ0(U0.90) = 0.45 и
U0.90 = 1.65 (см. таблицу 1 ПРИЛОЖЕНИЯ) . Объём выборки n = 30, вычисленный по выборке корреляционный коэффициент rξη = 0.9485. Тогда
16

V |
1 |
ln |
1 rξη |
|
1 |
ln |
1 0.9485 |
|
1 |
ln(37.8350) |
1.8166 |
|
2 |
1 r |
2 |
1 0.9485 |
2 |
||||||||
|
|
|
|
|
|
|
||||||
|
|
|
ξη |
|
|
|
|
|
|
|
|
и
th(1.499)< th(2.134) .
Вычислив гиперболические тангенсы, получим искомый доверительный интервал:
0.905 < ρ < 0.972.
ГЛАВА 2. РЕГРЕССИОННЫЙ АНАЛИЗ
егрессия (лат. regressio — обратное движение, отход), в теории вероятностей и математической статистике, зависимость математического ожидания (например, среднего значения) какой-либо случайной величины η от одной ξ или нескольких других случайных величин (независимых переменных). Такая зависимость между случайными величинами называется стохастической и описывается условным математическим ожиданием:
y(x) M | x f (x), |
(2.1) |
которое, как видно из записи, является функцией от независимой переменной x, имеющей смысл возможного значения случайной величины ξ. Соответственно y - возможные значения случайной величины η.
Уравнение y = y(x) = f(x) называется уравнением регрессии на ξ. Переменная x
называется регрессионной переменной или регрессором. График функции y = f(x) на-
зывается линией или кривой регрессии. Корреляционный анализ - поиск функции f(x).
Кривые регрессии η на x дают наилучшее в среднеквадратическом смысле предсказание значения величины η по заданному значению ξ = x. Иными словами, среди всех действительных функций φ(x) минимум M[(η- φ(x))2] достигается для функции φ(x) = M[η|ξ= x]. На практике это свойство используется для прогноза η по известному ξ:
Если модуль коэффициента корреляции близок к 1, то, как мы писали выше, зависи-
мость η от ξ стремиться к линейной. Линейная регрессия: |
|
y A Bx |
(2.2) |
наиболее простой, но важный случай.
Коэффициенты A и B можно найти из условия минимума F(A,B) = M[(η - A - Bξ)2]. Приравнивая к нулю частные производные
F A, B 2M
A
F A, B 2M
B
η A Bξ |
2 M η |
A BM ξ |
0, |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
ξ η A Bξ |
|
2 |
M |
|
ξ |
|
|
ξ |
|
BM |
|
ξ |
2 |
0, |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17

и решая систему двух линейных алгебраических уравнений относительно A и B, нетрудно получить:
B |
Kξη |
r |
|
Dη |
r |
ση |
и A M[ ] BM[ ] m r |
ση |
m , |
|
|
|
|
|
|
||||||
|
Dξ |
ξη |
|
Dξ |
ξη σξ |
|
ξη σξ |
ξ |
||
|
|
|
||||||||
где mξ, mη - |
математические ожидания случайных величин ξ и η. |
|||||||||
ветственно их дисперсии и среднеквадратические отклонения, |
rξη |
|||||||||
реляции величин ξ и η. |
|
|
|
|
||||||
Уравнением регрессии является прямая линия
Dξ, Dη и σξ, ση - соот- - коэффициент кор-
y(x) m rξη |
ση |
x mξ , |
(2.3) |
|
|
||||
|
σ |
ξ |
|
|
|
|
|
||
проходящая через точку (mξ, mη) с угловым коэффициентом
k rξη ση ,
σξ
называемым коэффициентом регрессии η на x.
Заметим, что целью построения линейной регрессии является подгонка прямой линии по точкам, так, чтобы минимизировать квадраты отклонений этой линии от наблюдаемых точек. Поэтому, эту общую процедуру иногда называют оценкой по методу наименьших квадратов.
Пример 2. Воспользовавшись данными из Табл.5, найти кривую регрессии, в том числе и уравнение прямой линейной регрессии.
Таблица 5. Результаты измерений роста ξ (см) и веса η (кг) 50 мужчин – слушателей академии МЧС.
η |
[55,65) |
[65,75) |
[75,85) |
[85,95) |
[95,105] |
nl |
|
ξ |
Y1= 60.0 |
Y2= 70.0 |
Y3= 80.0 |
Y4= 90.0 |
Y5= 100.0 |
||
|
|||||||
[155,160) |
4 |
2 |
0 |
0 |
0 |
6 |
|
X1 =157,5 |
|||||||
|
|
|
|
|
|
||
[160,165) |
3 |
3 |
1 |
0 |
0 |
7 |
|
X2 =162,5 |
|||||||
|
|
|
|
|
|
||
[165,170) |
1 |
3 |
2 |
0 |
0 |
6 |
|
X3 =167,5 |
|||||||
|
|
|
|
|
|
||
[170,175) |
0 |
4 |
3 |
1 |
0 |
8 |
|
X4 =172,5 |
|||||||
|
|
|
|
|
|
||
[175,180) |
0 |
0 |
2 |
4 |
0 |
6 |
|
X5 =177,5 |
|||||||
|
|
|
|
|
|
||
[180,185) |
0 |
0 |
1 |
4 |
1 |
6 |
|
X6 =182,5 |
|||||||
|
|
|
|
|
|
||
[185,190) |
0 |
0 |
1 |
2 |
1 |
4 |
|
X7 =187,5 |
|||||||
|
|
|
|
|
|
||
[190,195) |
0 |
0 |
1 |
3 |
3 |
7 |
|
X8 =192,5 |
|||||||
|
|
|
|
|
|
||
nk |
8 |
12 |
11 |
14 |
5 |
50 |
|
|
|
|
|
|
|
|
18

|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
||
Решение: |
|
|
x |
1 |
l1xl nl |
174.50, |
|||||||||
|
|
70 |
|||||||||||||
|
|
1 |
|
8 |
|
|
|
|
|
|
|
|
|
||
D |
l1xl |
2nl x 2 129.00, |
|
||||||||||||
70 |
|
||||||||||||||
D* |
= |
|
D |
|
1 |
5 |
y 2n y 2 155.36, |
||||||||
|
|
||||||||||||||
η |
|
|
|
|
|
70 k 1 |
k |
k |
|
||||||
|
|
|
|
|
|
||||||||||
|
|
|
1 |
8 |
|
|
5 |
|
|
|
|
|
|
||
Kξη* |
|
xl yk nlk |
xy 118.6, |
||||||||||||
|
|
||||||||||||||
|
|
|
70 l 1 k |
1 |
|
|
|
|
|
||||||
Тогда, уравнение линейной регрессии:
1 5
y 70 k 1yk nk 79.20,
σ* 11.36,
ση* 12.46,
K *
r σ*σξη* 0.8378.
ξ η
σ*
y(x) y rξη* ση* (x x)
ξ
после подстановки входящих в него величин примет вид:
y(x) 79.20 0.9194(x x) = 0.9194x 79.20 0.9194 174.50,
(2.4)
y(x) 0.9194x -81.235.
Для того, чтобы найти кривую регрессии согласно формуле y(x) = M[η|ξ=x] = f(x), на-
до вычислить условное математическое ожидание y(xῖ) [ 1 ]:
|
|
|
|
|
|
y(x%) M | x |
5 |
|
|
|
|
|
|
||
|
|
|
|
|
|
y n , |
|
|
|
||||||
|
|
|
|
|
|
l |
|
% |
k |
% |
|
|
|
||
|
|
|
|
|
|
|
l |
k 1 |
k|l l |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
n % |
|
|
|
|
|
|
|
|
|
|
||
где nk|l l% |
kl |
|
|
|
|
|
|
|
|
|
|
||||
n |
% - условное распределение случайной величины η при ξ= xῖ. |
|
|||||||||||||
|
|
|
l |
l |
|
|
|
|
|
|
|
|
|
|
|
Таблица 6. |
Условные распределения nkl=ῖ и условное математическое ожидание y(xῖ) |
||||||||||||||
случайной величины η. |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
η |
|
Y1= 60.0 |
Y2= 70.0 |
Y3= 80.0 |
|
Y4= 90.0 |
Y5= 100.0 |
|
y(xῖ) |
||||
|
ξ |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X1 =157,5 |
|
0,66666667 |
0,33333333 |
0 |
|
|
|
0 |
0 |
|
63.33 |
|||
|
X2 =162,5 |
|
0,42857143 |
0,42857143 |
0,14285714 |
|
|
0 |
0 |
|
67.14 |
||||
|
X3 =167,5 |
|
0,16666667 |
|
0,5 |
0,33333333 |
|
|
0 |
0 |
|
71.67 |
|||
|
X4 =172,5 |
|
0 |
|
0,5 |
0,375 |
|
0,125 |
0 |
|
76.25 |
||||
|
X5 =177,5 |
|
0 |
|
0 |
0,33333333 |
|
0,6667 |
0 |
|
86.67 |
||||
|
X6 =182,5 |
|
0 |
|
0 |
0,16666667 |
|
0,6667 |
0,166667 |
|
90.00 |
||||
|
X7 =187,5 |
|
0 |
|
0 |
0,25 |
|
|
0,5 |
0,25 |
|
90.00 |
|||
|
X8 =192,5 |
|
0 |
|
0 |
0,14285714 |
|
0,4286 |
0,428571 |
|
92.86 |
||||
Числа |
nkl=ῖ расположены на пересечении строк и столбцов таблицы, столбец |
|
|||||||||||||
y(xῖ) = |
f(xῖ) |
позволяет по точкам построить кривую регрессии. |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19 |

Найденные кривые регрессии на рис.6 представлены на фоне корреляционного поля.
Вес (кг)
95
90
85
отклонение линии регрессии
от наблюдаемой точки А
80
A
75
70
65
60
155 |
160 |
165 |
170 |
175 |
180 |
185 |
190 |
195 |
Рост (см)
Рис. 6
Построенная нами кривая регрессии φ(x) - это функция, которая среди всех действительных функций наилучшим образов описывает наблюдаемые точки в среднеквадратическом, то есть именно для этой функции достигается минимум M[(η- φ(x))2].
Найденная прямая y(x)=0.9194x - 81.235 (линейная регрессия) даёт наилучшее описание в смысле минимума суммы квадратов отклонений прямой от наблюдаемых точек среди всех линейных функций. Для примера, на рис. 6 показано отклонение прямой y(x)=0.9194x - 81.235 от некоторой точки A.
Линии регрессии (φ(x) |
и y(x)=0.9194x - 81.235) позволяют смоделировать поведение |
случайной величины η |
в зависимости от величины ξ, сделать необходимый прогноз. |
20
