4.1.2. Уточненное описание структуры выбора с многими отношениями предпочтения. Общая постановка задач векторной оптимизации

Обобщенная структура выбора с мультипредпочтением, описывающая задачи векторной оптимизации, имеет следующий вид:

s ,{ri }i ,{Fk }k 1

где s — множество допустимых альтернатив;

{ri }i — множество исходных отношений предпочтения;

{Fk }k 1 — множество правил согласований отношений предпочтения.

SPIIRAS

11

4.1.2. Уточненное описание структуры выбора с многими отношениями предпочтения. Общая постановка задач векторной оптимизации

называется шкалой оценок по критериальной функции fi. В дальнейшем в данной главе ограничения общности будем предполагать, что каждую критериальную функцию fi необходимо максимизировать (т.е. большие значения критериальных функций предпочтительнее меньших), а предпочтения ЛПР не меняются скачком. Кроме того, для

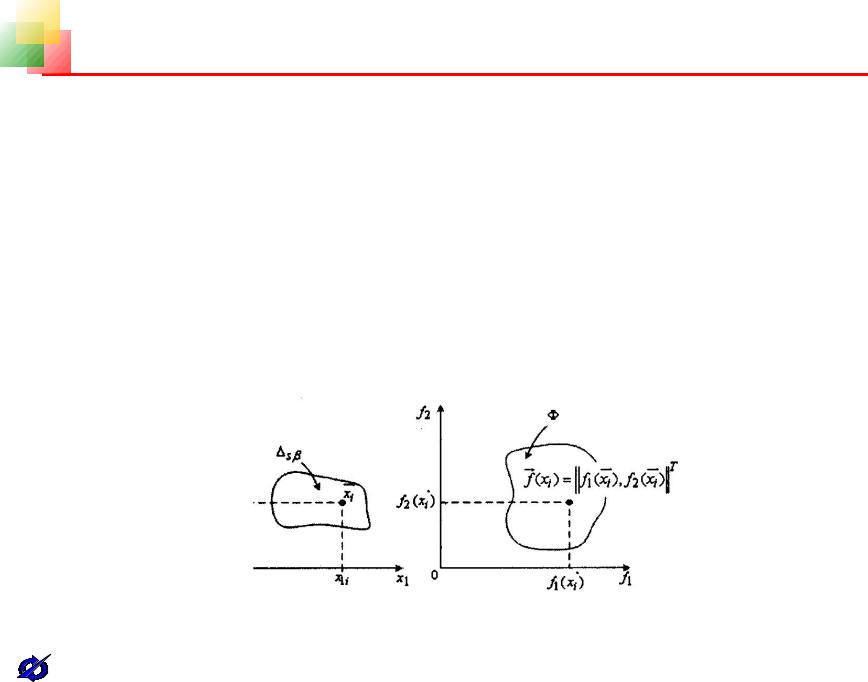
4.1.2. Уточненное описание структуры выбора с многими отношениями предпочтения. Общая постановка задач векторной оптимизации

На рис.4.1 для случая m=n=2 приведена используемая обычно для пояснения сущности проблем многокритериального выбора геометрическая интерпретация

пространства допустимых альтернатив s и пространства целевых (критериальных) функции , f f1, f2 T .

Конечной целью исследования задач векторной оптимизации обычно является отыскание некоторой наилучшей (оптимальной, эффективной) альтернативы,

принадлежащей множеству допустимых альтернатив s . При этом в настоящее

время известно большое разнообразие вариантов задания множества s , каждый из которых соответствует конкретной модели, относящейся, например, к классу математических, логико-лингвистических либо логико-алгебраических моделей.

Рис. 4.1.

SPIIRAS

13

4.2. Множество эффективных альтернатив и его основные свойства

4.2.1.Принцип В.Парето в задачах многокритериального выбора

Вп.4.1 было установлено, что для корректного решения задач многокритериального выбора необходимо в исходную постановку задачи (4.1) (4.2) привнести дополнительную информацию, позволяющую провести ее регуляризацию и построить результирующее

отношение предпочтения. Данная информация может задаваться по- разному. Наиболее глубокий подход к построению rðåçk предполагает выяснение возможности подчинения этого построения определенной аксиоматике. Одна из известных систем аксиом была сформулирована

Эрроу. Важное место среди других аксиом принадлежит аксиомам, связанным с принципом Парето. Данный принцип в общем случае может быть сформулирован с использованием двух определений.

SPIIRAS

14

4.2.1. Принцип В.Парето в задачах многокритериального выбора

Определение 4.1. Альтернативы удовлетворяют отношению

Данное определение можно задать в виде единого соотношения вида: xr y (i )(xri y) (i0 )(x i0 y)

Данное определение также можно задать с использованием единого

соотношения вида:

x y (i )(x i y)

SPIIRAS

15

4.2.1. Принцип В.Парето в задачах многокритериального выбора

Отношение доминирования по Парето в задачах многокритериального

запишется следующим образом:

(x, y s )(xr y (i )( fi (x) fi ( y)) (i0 )( fi0(x) fi0 ( y)) . Перечисленные представления принципа Парето, во-первых, определяют паретовскую аксиоматику, которой в числе прочих должно удовлетворять результирующее отношение предпочтения, и, во-вторых, используя (4.4)–(4.6) можно непосредственно осуществлять построение результирующего отношения предпочтения.

SPIIRAS

16

4.2.1. Принцип В.Парето в задачах многокритериального выбора

Замечание. Везде далее при постановке и решении задач многокритериального выбора будем предполагать выполненной (справедливой) аксиому независимости от непричастных альтернатив. Из данной аксиомы следует, что результат сравнения альтернатив x и y зависит только от них и не зависит от наличия или отсутствия некоторой третьей альтернативы z. Данная аксиома независимости должна восполняться и для соответствующих критериальных функций. Поясним это на примере.

SPIIRAS

17

4.2.1. Принцип В.Парето в задачах многокритериального выбора

Пример 4.3. Пусть при управлении ПО ЛПР руководствуется тремя показателями (критериальными функциями): f1 — характеризует общий объем выполненных операций, f2 — характеризует время, оставшееся до конца планового периода управления, f3 — оценивает дополнительные затраты, связанные с обеспечением выполнения запланированных операций.

Если объем выполненных операций высок и имеется большой резерв времени до момента времени tf, то дополнительно активизировать деятельности ПО нет необходимости, т.е. ЛПР будет предпочитать меньшие значения f большим. Если выполнение комплекса операций под угрозой (недопустимо низкие значения f1 и f2), то ЛПР скорее всего предпочтет увеличение f3 (увеличение дополнительных затрат), а не срыв выполнение боевой задачи. Таким образом, направление предпочтения по показателю f3 зависит от того, какие значения принимают показатели f1 и f2.

SPIIRAS

18

4.2.1. Принцип В.Парето в задачах многокритериального выбора

Показатель f3 называется зависимым по предпочтению от остальных

показателей. Используя приведенные выше правила определения предпочтительности альтернатив, принадлежащих множеств s , можно в указанном множестве выделить множество недоминируемых (по Парето) или,

состоит в том, что если это множество не пусто, то всякая альтернатива, лежащая вне множества Парето, доминируется альтернативой, принадлежащей последнему множеству. Следовательно, рационально поиск наилучших, в том или ином смысле, альтернатив сосредоточить именно в области Парето. Так как точки множества Парето не доминируют друг с друга, то переход между этими

окончательный выбор во множестве Парето связан с достижением определенного компромисса. Поэтому данное множество получило также название множества (области) компромиссов.

Дадим строгое определение понятию эффективной (недоминируемой по Парето) альтернативы.

SPIIRAS

19

4.2.1. Принцип В.Парето в задачах многокритериального выбора

Определение 4.3. Альтернатива называется эффективной (недоминируемой), если во множестве допустимых альтернатив не существуют решения, которое доминирует по Парето альтернативу x.

Определение эффективной альтернативы формально можно записать в следующем виде:

Следует отметить, что в отдельных монографиях или статьях эффективную (недоминируемую) альтернативу также называют паретовской, неулучшаемой альтернативой.

Приведем три примера, иллюстрирующих введенные выше понятия.

SPIIRAS

20