
- •Модели многокритериального оценивания и анализа качества программного обеспечения и методы его оценивания
- •Содержание
- •4.1. Структура выбора со многими отношениями предпочтения
- •4.1.1. Характерные особенности задач многокритериального выбора
- •4.1.1. Характерные особенности задач многокритериального выбора
- •4.1.1. Характерные особенности задач многокритериального выбора
- •4.1.1. Характерные особенности задач многокритериального выбора
- •4.1.1. Характерные особенности задач многокритериального выбора
- •4.1.1. Характерные особенности задач многокритериального выбора
- •4.1.1. Характерные особенности задач многокритериального выбора
- •4.1.2. Уточненное описание структуры выбора с многими отношениями предпочтения. Общая постановка задач векторной
- •4.1.2. Уточненное описание структуры выбора с многими отношениями предпочтения. Общая постановка задач векторной
- •4.1.2. Уточненное описание структуры выбора с многими отношениями предпочтения. Общая постановка задач векторной
- •4.2. Множество эффективных альтернатив и его основные свойства
- •4.2.1. Принцип В.Парето в задачах многокритериального выбора
- •4.2.1. Принцип В.Парето в задачах многокритериального выбора
- •4.2.1. Принцип В.Парето в задачах многокритериального выбора
- •4.2.1. Принцип В.Парето в задачах многокритериального выбора
- •4.2.1. Принцип В.Парето в задачах многокритериального выбора
- •4.2.1. Принцип В.Парето в задачах многокритериального выбора
- •4.2.1. Принцип В.Парето в задачах многокритериального выбора
- •4.2.1. Принцип В.Парето в задачах многокритериального выбора
- •4.2.1. Принцип В.Парето в задачах многокритериального выбора
- •4.2.1. Принцип В.Парето в задачах многокритериального выбора
- •4.2.1. Принцип В.Парето в задачах многокритериального выбора
- •4.2.2. Основные свойства множества Парето
- •4.2.2. Основные свойства множества Парето
- •4.2.2. Основные свойства множества Парето
- •4.2.2. Основные свойства множества Парето
- •4.2.2. Основные свойства множества Парето
- •4.2.2. Основные свойства множества Парето
- •4.2.2. Основные свойства множества Парето
- •4.2.2. Основные свойства множества Парето
- •4.2.2. Основные свойства множества Парето
- •4.2.3. Методы построения множества Парето
- •4.2.3. Методы построения множества Парето
- •4.2.3. Методы построения множества Парето
- •4.2.3. Методы построения множества Парето
- •4.2.3. Методы построения множества Парето
- •4.2.3. Методы построения множества Парето
- •4.2.3. Методы построения множества Парето
- •4.3. Классификация современных методов решения задач многокритериального выбора
- •4.3. Классификация современных методов решения задач многокритериального выбора
- •4.3. Классификация современных методов решения задач многокритериального выбора
- •4.3. Классификация современных методов решения задач многокритериального выбора
- •4.3. Классификация современных методов решения задач многокритериального выбора
- •4.3. Классификация современных методов решения задач многокритериального выбора
- •Требования к выбору методов многокритериального
- •Технология разрешения критериальной неопределенности
- •4.3. Классификация современных методов решения задач многокритериального выбора
- •4.4. Методы покомпонентного построения результирующих отношений предпочтения
- •4.4. Методы покомпонентного построения результирующих отношений предпочтения
- •4.4. Методы покомпонентного построения результирующих отношений предпочтения
- •4.4. Методы покомпонентного построения результирующих отношений предпочтения
- •4.4. Методы покомпонентного построения результирующих отношений предпочтения
- •4.4. Методы покомпонентного построения результирующих отношений предпочтения
- •4.5. Методы построения результирующих отношений предпочтения на основе свертки показателей
- •Методы скаляризации (свертки показателей)
- •4.5. Методы построения результирующих отношений предпочтения на основе свертки показателей
- •4.5. Методы построения результирующих отношений предпочтения на основе свертки показателей
- •4.5. Методы построения результирующих отношений предпочтения на основе свертки показателей
- •4.5. Методы построения результирующих отношений предпочтения на основе свертки показателей
- •4.5. Методы построения результирующих отношений предпочтения на основе свертки показателей
- •4.5. Методы построения результирующих отношений предпочтения на основе свертки показателей
- •4.5. Методы построения результирующих отношений предпочтения на основе свертки показателей
- •4.5. Методы построения результирующих отношений предпочтения на основе свертки показателей
- •4.5. Методы построения результирующих отношений предпочтения на основе свертки показателей
- •4.5. Методы построения результирующих отношений предпочтения на основе свертки показателей
- •Основные недостатки скаляризации
- •Метод анализа иерархий (метод Томаса Саати)
- •Обобщенная иерархия
- •Этапы МАИ
- •Этапы МАИ
- •шкала словесных определений уровня важности
- •общее удовлетворение школой
- •матрицы локальных приоритетов
- •Этапы МАИ
- •Этапы МАИ
- •Постановка задачи
- •Модель модернизации ИС кафедры
- •Графическое представление путей модернизации
- •Характерные сценарии модернизации ИС кафедры
- •Алгоритм решения задачи
- •Результаты решения машинного
- •Результаты решения машинного
- •Результаты решения машинного
- •Результаты решения машинного
- •Результаты решения машинного
- •Результаты решения машинного
- •Результаты решения машинного
- •Методика сопоставления пакетов математических подпрограмм
- •Алгоритм построения интегрального показателя
- •Технология разрешения критериальной неопределенности. Ортогональный план экспертного опроса
- •Построение ортогонального плана экспертного опроса
- •Иллюстративные примеры. Пример 2
- •Результаты вычисления
- •Программные комплексы для управления проектами
- •Сложность сравнения
- •Требования к методике сопоставления
- •Показатели
- •Методика многокритериального выбора
- •Шкалы и ортогональный план
- •Результирующий показатель
- •Алгоритм методики
- •Результат сравнительного анализа
- •Публикации
- •Публикации
- •Публикации
- •Публикации
- •Проведение экспертного опроса
- •Построение ортогонального плана экспертного опроса
- •Построение результирующего показателя
- •выбор школы
- •оценки
- •общее удовлетворение школой
- •матрицы локальных приоритетов
- •оценки школ
4.2.1. Принцип В.Парето в задачах многокритериального выбора
|
|
|
||
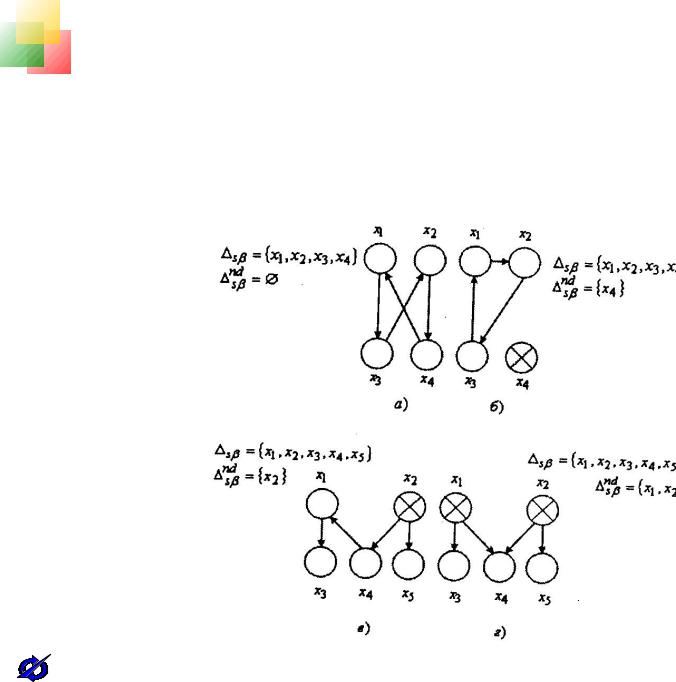
Пример 4.4. В задачах группового выбора часто используют графический способ |
||||
|
|
|
|
|
задания отношений предпочтения на множествеrдопустимых альтернатив. В этом |
||||
|
|
i |
|
|
случае альтернативам соответствуют вершины соответствующих графов, а ребра |
||||
задают отношения предпочтения. На рисунке 4.2 |
а,б,в,г приведены варианты |
|||
задания множества |
. Элементы множества |
nd |
||
на рисунках помечены |
||||
крестиками. nds |
|
s , s |
||
|
|
|
||
SPIIRAS
21

4.2.1. Принцип В.Парето в задачах многокритериального выбора
Пример 4.5. Пусть имеется три допустимых варианта создания ПОs ={x1,x2,x3}, каждый из которых характеризуется вектором
критериальных |
функций |
|
(вектором показателей |
|
эффективности): |
||||||||||||||||||||||||||||||||||||
f |
|
f |
1 |
, f |
2 |
, f |
3 |
|
T |
f (x |
) |
|
|
|
1,2,4 |
|
|
|
T , f (x |
2 |
) |
|
|
|
2,3,1 |
|
|
|
T , f (x |
3 |
) |
|
|
|
1,3,5 |
|
|
|
T |
. Так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
, причем |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
каждая компонента вектора f (x1 ) доминируется соответствующими
компонентами вектора |
nd |
|
f (x3 ) , то альтернатива x1 s ; альтернативы |
||
x2 и x3 не доминируют друг друга, т.к. f1(x2 ) f1(x3 ), но |
f3(x2 ) f3(x3,) |
|
|
nd |
|
f2(x2 ) f2(x3 ) . Поэтому s x2 , x3 . |
|
|
SPIIRAS
22

4.2.1. Принцип В.Парето в задачах многокритериального выбора
Пример 4.6. В двухкритериальных задачах линейного программирования с двумя неизвестными можно достаточно наглядно представить множество Парето (множество компромиссов) как в
пространстве альтернатив, так и в пространстве целевых функций. В |
|||||||||||||||||||||||||||||||||||||
самом деле, пусть f |
|
|
|
f1, |
|
f2 |
|
|
|
T |
, где |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
f1(x) c11 x1 c12 x2; f2(x) c21 x1 c22 x2; |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
x1, x2 |
|
|
|
T |
|
|
|
|
|
|
|
c11 ,c12 |
|
|
|
T |
|
|
|
|
|
c21,c22 |
|
|
|
T . |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
x |
|
|
|
|
|
|
|
;c1 |
|
|
|
|
|
|
|
;c2 |
|
|
|
|
|
|
|
|
|||||||||||||
Множество допустимых |
|
альтернатив |
в |
рассматриваемой |
задаче |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||
зададим в виде системы линейных неравенств: aij xi bj ; j 1,2 |
. Тогда |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
||||
по аналогии с рисунком 4.1 зададим в пространстве альтернатив и критериальных функций соответствующие множества, которые в графическом виде представим на рисунке 4.3.
SPIIRAS
23

4.2.1. Принцип В.Парето в задачах многокритериального выбора
Рис. 4.3.
SPIIRAS
24

4.2.1. Принцип В.Парето в задачах многокритериального выбора
На рисунке 4.3 области Парето альтернатив в пространстве и образ области Парето критериальных функций изображены на качественном уровне (без указания конкретных координат характерных точек указанных множеств). При этом в пространстве s множеству Парето принадлежат точки, лежащие на гранях M1M2,M2M3. Точка M5 является неэффективной, так как доминируется,
например, точкой M2. В пространстве критериальных функций образами точек, принадлежащих граням M1M2,M2M3, являются точки, принадлежащие граням N1N2,N2N3, которые, в свою очередь, образуют образ множества Парето в пространстве целевых функций. Конкретный вариант задания указанных множеств для задач линейного программирования будет приведен в конце данной главы.
Важным практическим результатом выделения области компромиссов (множества Парето) является существенное сужение области поиска оптимальных решений. В связи с этим весьма актуально и полезно получать в явном виде решения из области компромиссов и предъявлять их ЛПР. Для этого необходимо изучить свойства множества Парето и методы его построения.
SPIIRAS
25

4.2.2. Основные свойства множества Парето
|
|
|
|
Рассмотрим основные свойства множества Парето (множества |
nd |
и |
|
s |
|||
соответственно nd). При этом, как и ранее будем предполагать, что все целевые функции максимизируются.
Свойство №1. Никакие альтернативы, принадлежащие множеству допустимых альтернатив s , не доминируют (не превосходят) альтернативы, принадлежащие множеству Парето.
Свойство №2. При переходе от одной точки (альтернативы) множества Парето к другой точке множества Парето происходит увеличение значений одних критериальных функций и уменьшение значений других критериальных функций.
Свойство №3. Множеству Парето принадлежат все альтернативы x s , при которых достигается единственные (или глобальные) экстремумы значений хотя бы одной из критериальных функций fi (i ) , как при отсутствии ограничений на значения остальных критериальных функций, так и при вводе (частичном вводе) таких ограничений. Другими словами, множеству Парето принадлежат альтернативы xi* , для которых
xi* argmax fi (x), i 1,2,...,m
x s
SPIIRAS
26

4.2.2. Основные свойства множества Парето
Свойство №4. Множеству Парето принадлежат все точки x s , в которых достигается единственный (или глобальный) экстремум линейных форм вида
i fi (x) max |
(4.8) |
|
i |
x s |
|
где i 1, 0(i ). При этом |
s должно быть ограниченным и замкнутым |
|
i |
fi (x) непрерывны. |
|
множеством (компакт), а функции |
|
|
Свойство №5. Если множество альтернатив s является выпуклым компактом и соответствующим требованиям вогнутости (выпуклости) удовлетворяют непрерывные функции fi, то решение совокупности указанных выше экстремальных задач вида (4.8) в принципе определяет все точки множества Парето.
Важное свойство множества, не связанное с предположением о выпуклостиnd , было обнаружено Ю.Б. Гермейером.
SPIIRAS
27

4.2.2. Основные свойства множества Парето
Свойство №6. Любая точка множества Парето, расположенного в строго положительном варианте, может быть представлена как решение задачи
max min i fi ( x) |
(4.9) |
x s i |
|
при соответствующем подборе коэффициентов, на которые накладывается
условие i 0(i ), i 1. При этом |
s — компакт, |
fi(i Г) непрерывны. |
i |
|
|
Важную роль в задачах векторной оптимизации играет точка в пространстве критериальных функций , в которой все критериальные функции принимают экстремальные значения (в данном случае максимальные значения).
Пусть fi*(i ) — максимальные значения каждой критериальной функции. Эта точка может иметь прообраз в пространстве альтернатив xèä s в том идеальном случае, при котором в этой точке одновременно достигается максимум по всем указанным функциям. На рисунке 4.3 данная точка обозначена вектором fèä* .
SPIIRAS
28

4.2.2. Основные свойства множества Парето
На рисунке 4.4 изображена ситуация, при которой точка fèä* имеет прообраз (точку) в пространстве альтернатив, которая является единственной точкой множества Парето. Данную точку называют идеальной (утопической) точкой множества Парето. Нахождение идеальной точки во многих случаях оказывается весьма полезным при постановке задач определения реальной точки выбора. Кроме того, компоненты утопической точки fèä* часто используют для нормализации соответствующих критериальных функций.
Рис. 4.4.
SPIIRAS
29
4.2.2. Основные свойства множества Парето
В заключение данного подпункта остановимся на особенностях графического
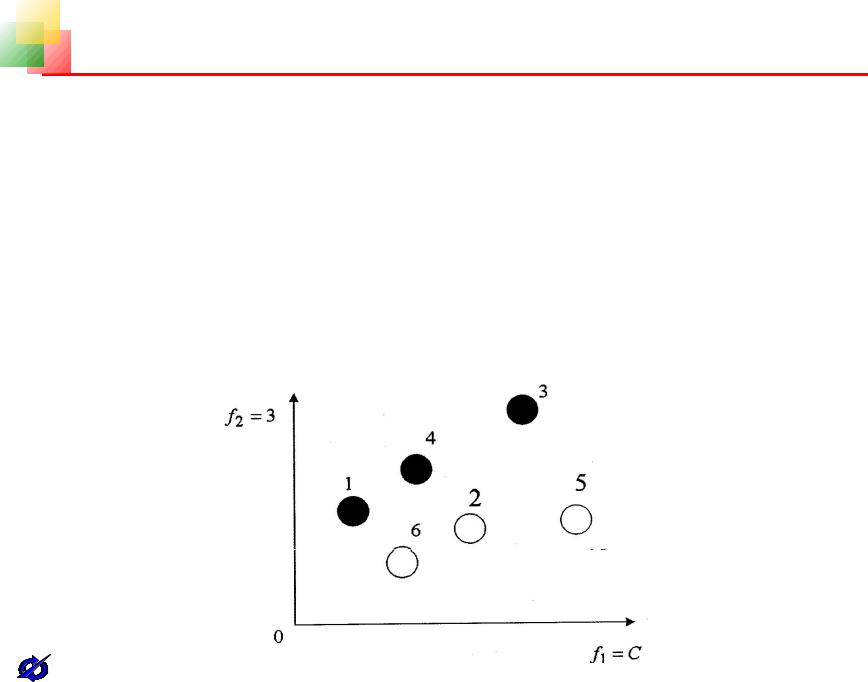
задания множеств nds и . Так, например, в случае решения двух или трех критериальных задач можно непосредственно находить точки множества Парето на основе анализа соответствующих графиков, задающих множество эффективных оценок. Данный подход лежит в основе реализации методов решения задач, в которых осуществляется оптимизация показателей, оценивающих эффективность и стоимость создания и применения, сложных организационно-технических систем. На рисунке 4.5 для примера построен график шести вариантов ПО, каждый из которых характеризуется своей стоимостью
создания и эксплуатации (показатель f1=C) и эффективностью применения (показатель f2=Э).
Рис. 4.5.
SPIIRAS
30
