Установочная лекция 2 (2 ч)

МЕТОДЫ РАСЧЕТА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

ПОСТОЯННОГО ТОКА

Дидактические единицы:

2.1. Метод расчета цепей, основанный на законе Ома.

2.2. Метод наложения.

2.3. Метод расчета цепей, основанный на законах Кирхгофа (МЗК)).

2.4. Метод контурных токов и метод узловых напряжений (метод двух узлов).

2.5. Метод эквивалентного генератора.

2.6. Мощность цепи постоянного тока. Баланс мощностей.

2.7. Потенциальная диаграмма замкнутого контура.

2.8. Особенности расчета нелинейной цепи постоянного тока

(для самостоятельного прочтения).

СОДЕРЖАНИЕ

Формулы эквивалентных преобразований в электрических цепях:

а) последовательное соединение резисторов и источников напряжения (ИН):

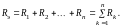
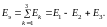
б) параллельное соединение резисторов:

дву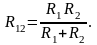х: трех: .

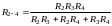в) правило делителя напряжений с последовательным соединением резисторов;

двух: 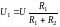и

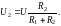
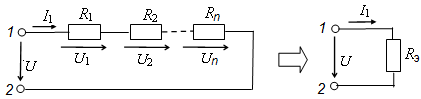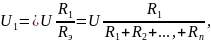
трех и более: 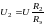и т.д.

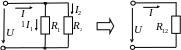г) правило делителя тока при параллельном соединении двух резисторов:

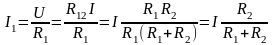и

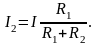
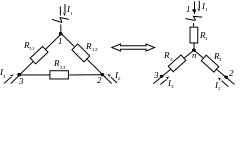д) соединения треугольником трех резисторов в эквивалентную звезду:

, .

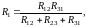
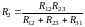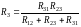д) соединения звездой трех резисторов в эквивалентный треугольник:

.

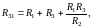
2.1. Метод расчета цепей, основанный на законе Ома

Этот метод при­ме­няют для расчёта простых цепей с одним источником энергии. При этом преобразовывают («свертывают») пассивную часть схемы цепи для: определения эквивалентного сопротивления относительно зажимов источника, затем входного тока и, посредством правила делителя тока, токов ветвей.

Найдем токи ветвей схемы цепи (рис. 2.1а) с параметрами: Е = 12 В, R_вт = 1 Ом, R₁ = = 4 Ом, R₂ = R₃ = 6 Ом.

1. Определяем эквивалентное сопро­тив­ление cхемы цепи относительно зажимов ин (рис. 2.1б):

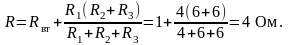
2. Ток на входе цепи I = E/R = 12/4 = 3 А.

3. Согласно правилу делителя тока:

,

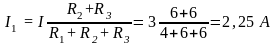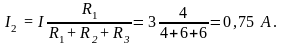
2.2. Метод наложения

Метод расчёта токов (напряжений) ветвей схемы линейной электрической цепи, содержащей источники напряжения и тока, основанный на определении частичных токов (напряжений) при по­очередном действии ЭДС E_k и токов J_k источников энергии и последу­ющим алгебраическом сложении полученных частичных токов 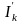(напряжений 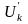) в каж­дой ветви, называют методом наложения решений, т.е.

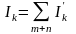и ,

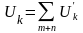где m и n  число источников соответственно напряжения и тока.

Внимание! При определении частичных токов (напряжений) вет­­вей от дей­ствия тока J_k или ЭДС E_k k-го источника энергии, ветви с остальными ИТ разрываются, а идеальные ИН замыкаются накоротко, однако внутренние сопротивления ИН сохраняются в соответствующих ветвях.

Определим токи ветвей схемы (рис. 2.2а) с параметрами: E₁ = 12 В, E₂ = 5 В, Е₂ = 2,4 В, R₁ = 2 Ом, R = 8 Ом, применив метод наложения.

1 . Выбираем произвольно направления токов i1, I и i2.

2. Вычерчиваем расчетную схему с одним ИН E₁ (рис. 2.2б) и определяем частичные токи от действия ЭДС E₁:

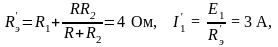
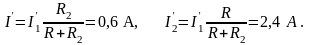
3. Вычерчиваем расчётную схему с ин e2 (рис. 2,2в) и находим частичные токи:

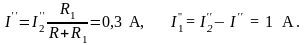
4. С учётом направлений частичных токов определяем токи в ветвях исходной электрической схемы:

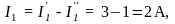
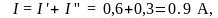
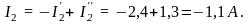
2.3. Метод расчета цепей, основанный на законах Кирхгофа (мзк)

Анализ и расчёт любой электрической цепи постоянного тока можно провести в результате совместного решения системы уравнений, составленных посредством первого и второго законов Кирхгофа.

Первый закон Кирхгофа (1ЗК) записывают для узлов электрической схемы: алгебраическая сумма токов в любом узле схемы цепи равна нулю, т.е. (соответственно для цепей постоянного и переменного тока):

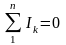и

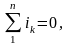
где I_k – ток k-й ветви, присоединённой к данному узлу; n  число ветвей, подключенных к узлу.

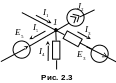
При этом токи, направленные к узлу, при­­нято записывать со знаком плюс, а уходящие от уз­ла, со знаком минус (рис. 2.3):

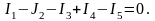
Второй закон Кирхгофа (2ЗК) применяется к контурам электрической цепи и формулируется следующим образом: в лю­бом контуре схемы алгебраическая сумма ЭДС равна ал­ге­браической сумме напряжений на всех участках с сопротивлениями, входящими в этот контур, т.е. (соответствен­­но для цепей постоянного и переменного токов):

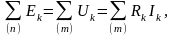
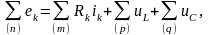
г де (n)  число ИН в контуре; (m), (p), (q)  число в нем резистивных, индук­тив­ных и ёмкостных элементов.

ЭДС и напряжения на элементах контура за­писывают со знаком плюс, если выбран­ное нап­равление обхода контура (например, по ходу часовой стрелки, рис. 2.4) совпадает с направлением напряжений (токов) на этих элементах, т.е.

E₁  E₄ = R₄I₄  R₁I₁  R₂I₂ + R₃I₃.

Если разомкнуть ключ S на участке 1-2 (см. рис. 2.4) (резистор R₃ отключен и ток I₃ = 0), то для этого же контура второй закон Кирхгофа запишется следу­ющим об­­разом:

E₁  E₄ = R₄I₄  R₁I₁  R₂I₂ + U₂₁.

Число уравнений по МЗК в системе равно числу ветвей в цепи (N_МЗК = В), при этом число независимых уравнений, которые можно запи­сать по 1ЗК, на од­но уравнение меньше числа узлов, т.е.

N_1ЗК = У  1,

а число независи­мых уравнений, записываемых по 2ЗК,

N_2ЗК = B  (У  1),

где В  число ветвей с неизвестными токами (без ветвей с источниками тока); У  число узлов.

Составим с помощью законов Кирхгофа необходи­мое число уравнений для определения токов ветвей схемы (рис. 2.5), если заданы ЭДС E₁ и E₂ источников напряжения, ток J источника тока и соп­ротивления R₁,…, R₅ резисторов.

1. Проведём топологический анализ схемы для определения числа независимых урав­­нений. В схеме B₁ = 6 вет­вей, У = 3 узла. Од­нако в ветви с ИТ ток J задан, поэтому число независимых ветвей В = 5. Число независимых урав­нений для решения задачи по методу законов Кирхгофа

N_МЗК = N_1ЗК + N_2ЗК = В.

2. Пронумеруем узлы и выберем произвольно направления токов в вет­вях (рис. 2.6).

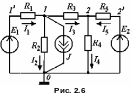3. Составим уравнения по 1ЗК (N_1ЗК = У  1 = 3  1 = 2):

для узла 1: I₁  I₂  J  I₃ = 0,

для узла 2: I₃  I₄ + I₅ = 0.

4. Выбираем независимые кон­ту­ры и направление обхода контуров, на­при­мер, по ходу часовой стре­лки. Имеем три независимых контура, так как ветвь с заданным током J ИТ в уравнениях, составленных по 2ЗК, не учитывается: N_2ЗК = B  (У  1) = 3.

5. Составим три уравнения по 2ЗК:

для контура 1'-1-0-1': E₁ = R₁I₁ + R₂I₂,

для контура 1-2-0-1: 0 = R₃I₃ + R₄I₄  R₂I₂,

для контура 2-2'-0-2: E₂ = R₅I₅  R₄I₄.

6. Решив систему из пяти уравнений, например, методом Гаусса или с использованием формул Крамера, можно определить все неизвестные токи ветвей цепи.

2.4а. Метод контурных токов

При расчёте сложных цепей методом законов Кирхгофа необходимо составить и решить систему алгебраических B-уравнений. Чтобы понизить порядок системы уравнений в методе контурных токов (МКТ), вместо токов ветвей определяют (по 2ЗК) так называемые контурные токи, замыкающиеся в контурах. Кон­тур­ный ток  условно расчётный ток, имеющий одинаковое значение на всех участках рассматриваемого контура-ячейки схемы це­пи. Составив и решив систему урав­не­ний относительно контурных токов, осу­ществляют переход от контурных то­ков к токам ветвей на основа­нии простейших соотношений.

Необходи­мое для расчёта цепи чис­ло уравнений по МКТ равно числу не­зависимых контуров, т.е.

N_МЗК = B  (У  1) = k_н.

Если схема содержит источники то­ка, то число независимых уравнений уменьшится на число n ветвей с источ­никами тока:

N_МКТ = N_2ЗК = B  (У  1)  n,

так как контурный ток ячейки с ИТ известен и равен току источника тока.

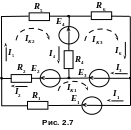
Определим токи ветвей схемы цепи (рис. 2.7) с параметрами E₁ = 100 В, E₂ = 30 В, E₃ = 10 В, E₄ = 6 В, R₁ = = R₃ = 10 Ом, R₄ = 7 Ом, R₅ = 5 Ом, R₆ = 15 Ом. В схеме ветвей В = 6, узлов У = 4.

1. Выбираем направления кон­­­­­­­турных токов I_К1, I_К2, I_К3 по ходу часовой стрелки.

2. Составим систему уравнений для кон­­­туров, в каждом из которых алгебраическая сумма ЭДС (контурная ЭДС) равна про­изведению контурного тока данной ячей­ки на сумму всех сопротивлений ячейки, минус про­изведения контурных токов соседних яче­­­­ек на соответствующие сопротивления общих ветвей.

Число уравнений по МКТ: N_МКТ=В  (У  1) = 6  (4  1) = 3,

E₁  E₂  E₃ = (R₁ + R₂)I_К1  R₂I_К2,

E₂  E₄ = (R₂ + R₅ + R₄)I_К2  R₄I_К3  R₂I_К1,

E₃ + E₄ = (R₆ + R₄)I_К3  R₄I_К2.

3. После подстановки числовых значений имеем:

60 = 20I_К1  10I_К2,

24 = 10I_К1 + 22I_К2  7I_К3,

16 = 7I_К2 + 22I_К3.

4. Решив эту систему, найдем контурные токи:

I_К1 = 5 А, I_К2 = 4 А, I_К3 = 2 А.

5. Токи ветвей определим, руководствуясь выбранными направлениями токов ветвей и правилами:

 токи наружных ветвей (не имеющих соседних контуров) равны соответствующим контурным токам;

 токи общих ветвей равны разности контурных токов соседних кон­ту­ров-ячеек:

I₁ = I_К1 = 5 А, I₅ = I_К2 = 4 А,

I₆ = I_К3 = 2 А, I₂ = I_К1  I_К2 = 5  4 = 1 А,

I₄ = I_К2  I_К3 = 4  2 = 2 А, I₃ = I_К1  I_К3 = 5  2 = 3 А.

2.4б. Метод узловых напряжений (метод двух узлов).

Метод узловых напряжений (МУН) базируется на первом законе Кирхгофа и обобщенном законе Ома. В нём за вспомогательные расчётные величины принимают так называемые узловые напряжения U_k0  напряжения между каждым k-м узлом схемы и выбранным базисным узлом (его будем обозначать цифрой 0), потенциал которого принимают равным нулю. Число уравнений для расчёта схемы по МУН

N_МУН = У  1.

Структура каждого уравнения одинаковая, например, уравнение относительно узла 1:

G₁₁U₁₀  G₁₂U₂₀  ...  G_1nU_n0 = +

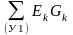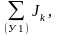
где G₁₁ = G₁ + G₂ + ... + G_n  собственная проводимость узла 1, равная сумме проводимостей ветвей, присоединённых к узлу 1 (проводимости ветвей с ИТ не учитываются, так как G_j = 1/R_j = 0 (R_j = )); G₁₂, ... , G_1n – меж­узловые проводимости; +  узловой ток узла 1;  алгебраическая сумма произведений ЭДС ветвей, присоединённых к узлу 1, на проводимости этих ветвей, причём со знаком плюс (минус) записывают произведения, если ЭДС направлена к узлу 1 (от узла 1);  алгебраическая сумма токов источников тока ветвей, подключённых к узлу 1, причём токи J_k записывают со знаком плюс (минус), если они направлены к узлу 1 (от узла 1).

Решив систему уравнений относительно узловых напряжений, определяют межузловые напряжения и токи ветвей по обобщенному закону Ома.

Метод двух узлов является частным случаем метода узловых напряжений и применяется для расчёта схем, содержащих (после преобразования) два узла и произвольное число параллельных пассивных и активных ветвей.

Для расчёта токов ветвей цепи составляют и решают одно уравнение узлового напряжения U₁₀, равное алгебраической сумме токов, создаваемых всеми источниками напряжения и источниками тока цепи, делённой на собственную проводимость узла G₁₁, т.е.

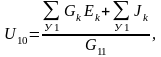
а токи ветвей определяют по обобщённому закону Ома.