4. Метод интегрирования по частям.

Этот метод наиболее часто применяется, если подынтегральная функция содержит логарифмические, показательные, обратные тригонометрические,

тригонометрические функции, а также их комбинации.

∫ = −∫ .

Некоторые типы функций, которые интегрируются с помощью метода интегрирования по частям и рекомендуемые разбиения:

I тип:

∫Pn(x) cos(kx) dx; ∫Pn(x) sin(kx) dx;

∫Pn(x) akx dx, ∫Pn(x) ekx dx

Здесь Pn(x) - многочлен степени n, k - некоторая константа. В данном случае в качестве функции u берется многочлен, а в качестве dv - оставшиеся сомножители. Для интегралов такого типа формула интегрирования по частям применяется n раз.

II тип:

∫Pn(x) lnkx) dx; ∫Pn(x) arccos(x) dx; ∫Pn(x) arcsin(x) dx; ∫Pn(x) arctg(x) dx; ∫Pn(x) arcctg(x) dx,

Здесь принимают, что dv =Pn(x)dx, а в качестве u оставшиеся сомножители.

III тип:

∫akx+bcos(nx+c) dx; ∫akx+bsin(nx+c) dx:

В данном случае в качество u берется либо экспонента, либо тригонометрическая функция. Единственным условием есть то, что при дальнейшем применении формулы интегрирования по частям в качестве функции u берется та же функция, то есть либо экспонента, либо тригонометрическая функция соответственно.

Отметим, что для вычисления интеграла, формула интегрирования по частям может применяться неоднократно.

Пример 21

Найти интеграл

В исходном интеграле выделим функции u и v, затем выполним интегрирование по частям.

Пример 22

Найти неопределенный интеграл Для вычисления этого интеграла будем использовать метод интегрирования по частям. Положим что

Тогда

Для вычисления последнего интеграла используем формулу из таблицы интегралов

тогда

Далее подставляя все в формулу интегрирования по частям, получим:

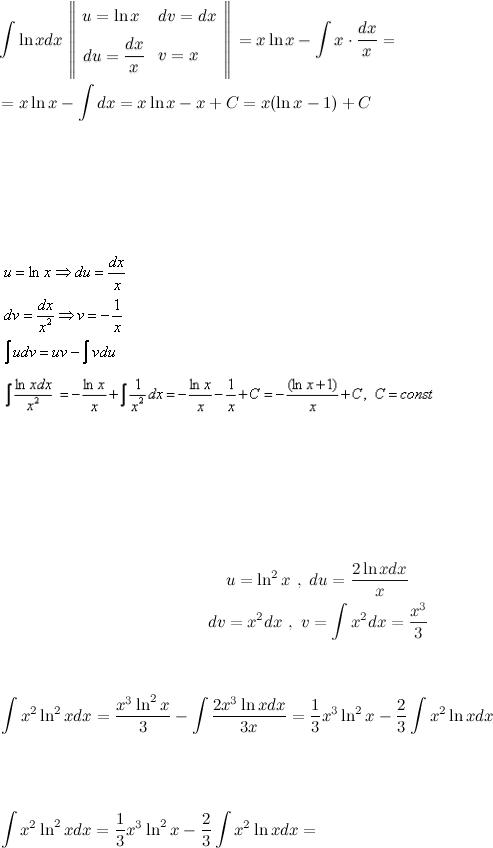
Пример23

Найти интеграл

В исходном интеграле выделим функции u и v , затем выполним интегрирование по частям.

Пример24

Найти неопределенный интеграл

Интегрируем по частям:

Пример25

Найти неопределенный интеграл Вычислим данный интеграл, используя метод интегрирования по частям. Для этого положим

И подставим полученные выражения, в формулу для интегрирования по частям

Для решения к полученному интегралу необходимо снова применить метод интегрирования по частям:

Пример26

Найти неопределенный интеграл

Дважды интегрируем почастям:

Пример27

Найти неопределенный интеграл Для вычисления данного интеграла сначала сделаем замену переменной:

а затем для нахождения полученного интеграла воспользуемся методом интегрирования по частям и таблицей интегралов:

Делая обратную замену, окончательно получим

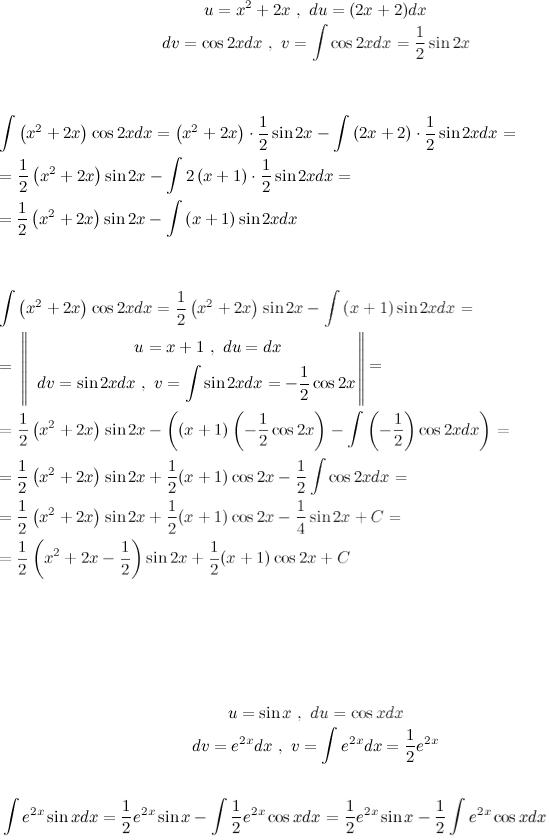
Пример28

Найти неопределенный интеграл Для решения данного интеграла воспользуемся методом интегрирования по частям. Положим что

Подставляя это в формулу интегрирования по частям, будем иметь:

К полученному интегралу снова применим метод интегрирования по частям:

Пример29

Найти неопределенный интеграл Вычислим заданный интеграл, используя метод интегрирования по частям. Положим

Далее, по формуле интегрирования по частям, имеем

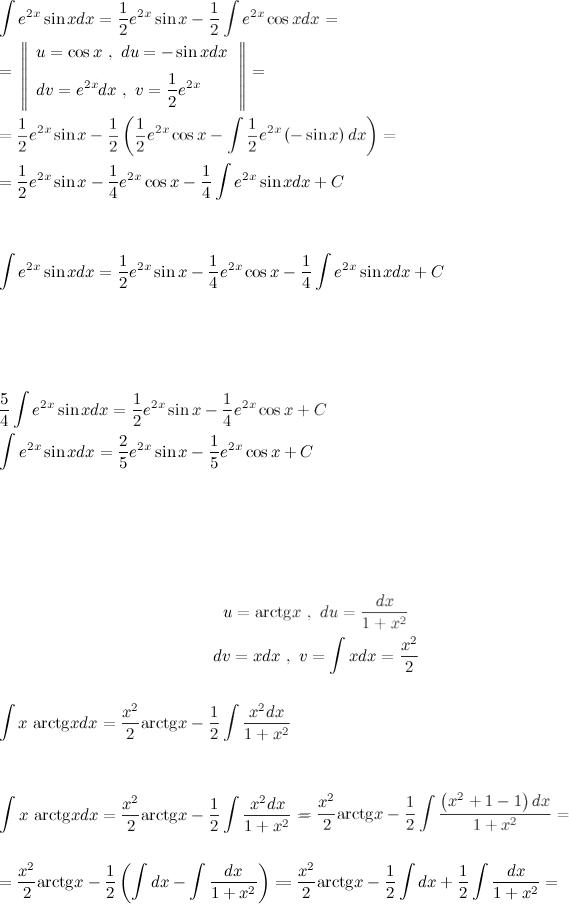
К полученному интегралу снова применим метод интегрирования по частям:

Таким образом, мы получили следующее равенство

Так как в левой и правой частях равенства есть искомый интеграл, то мы можем, перенеся его в одну часть, выразить чему равен искомый интеграл:

Пример30

Найти неопределенный интеграл Воспользуемся методом интегрирования по частям:

Подставим все в формулу интегрирования по частям:

Для нахождения полученного интеграла прибавим и вычтем в числителе 1, затем сгруппировав слагаемые в числитель разделим их на знаменатель:

Пример31

Найти неопределенный интеграл.

Интегрируем по частям:

Интеграл найден методом подведения функции под знак дифференциала, можно использовать и метод замены в «классическом» виде.

Пример33

Найти неопределенный интеграл 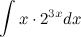Воспользуемся методом интегрирования по частям. Для этого положим