3. Метод замены переменной или метод подстановки
Метод замены переменной или метод подстановки. Этот метод заключается во введении новой переменной интегрирования (то есть делается подстановка). При этом заданный интеграл приводится к новому интегралу, который является табличным или с помощью преобразований его можно свести к табличному.
Пусть требуется вычислить интеграл |
. Сделаем подстановку |
. |
Тогда |
и интеграл принимает вид: |
∫ ( ) |
, |
или |
|
|
|
|
|
, т.е в подынтегральном выражении должна находиться некоторая |
функция |
|
. После решения интеграла |
|
делаем |
|
∫ ( ) и её производная |
|
обратную подстановку t = x.
Общее правило: за t обозначаем саму функцию (а не её производную).
Находим dt следующим образом:
1)записываем формулу подстановки: ϕ(t) = f(x);
2)заключаем функции в скобки со знаком производной и домножаем на dx и dt
соответственно: (ϕ(t))'dt =(f(x))'dx;
3)берем производные и выражаем dx через dt.
Например подстановка: t2 = (2x-1) → ( t2)' dt = (2x-1)'dx → 2tdt = 2dx →
→ dx = tdt Запомните это.
Пример 15.
Найти интеграл  Сделаем замену переменной:
Сделаем замену переменной:  , далее приведем интеграл к табличному виду и решим
, далее приведем интеграл к табличному виду и решим
его. В конце решения делаем обратную замену.
Пример 16
Найти интеграл  .
.
Упростим подынтегральную функцию, а потом сделаем замену переменной: 
Пример 17
Найти неопределенный интеграл 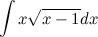 Введем замену
Введем замену 
Заменим интеграл суммы на сумму интегралов и вынесем постоянные коэффициенты.
Полученные интегралы находим как интегралы от степенной функции:
Делая обратную замену, окончательно получим
Пример 18
Найти неопределенный интеграл  Введем замену
Введем замену 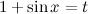 и полученный интеграл находим как интеграл от степенной функции:
и полученный интеграл находим как интеграл от степенной функции:
Сделаем обратную замену
Пример 19
Найти неопределенный интеграл  Введем замену и полученный интеграл находим как интеграл от обратной функции:
Введем замену и полученный интеграл находим как интеграл от обратной функции:
Выполним обратную замену
Пример 20
Найти неопределенный интеграл 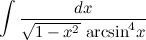 Введем замену и полученный интеграл находим как интеграл от степенной функции:
Введем замену и полученный интеграл находим как интеграл от степенной функции:
Выполним обратную замену и окончательно получим:



 Сделаем замену переменной:
Сделаем замену переменной:  , далее приведем
, далее приведем 


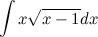 Введем замену
Введем замену 

 Введем замену
Введем замену 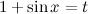 и полученный интеграл находим как интеграл от степенной функции:
и полученный интеграл находим как интеграл от степенной функции: Введем замену и полученный интеграл находим как интеграл от обратной функции:
Введем замену и полученный интеграл находим как интеграл от обратной функции: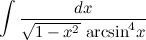 Введем замену и полученный интеграл находим как интеграл от степенной функции:
Введем замену и полученный интеграл находим как интеграл от степенной функции: