Пример4.
Вычислить неопределенный интеграл  Преобразуем заданный интеграл используя свойства интегралов, представим интеграл суммы в виде суммы интегралов:
Преобразуем заданный интеграл используя свойства интегралов, представим интеграл суммы в виде суммы интегралов:
Вынесем за знак интеграла из обеих дробей соответствующие коэффициенты при  :
:
Далее, используя таблицу интегралов, получим
2. Интегрирование внесением под дифференциал
Табличные формулы справедливы и применимы НЕ ТОЛЬКО для переменной x, но и для любого сложного выражения, ЛИШЬ БЫ АРГУМЕНТ ФУНКЦИИ И ВЫРАЖЕНИЕ ПОД ЗНАКОМ ДИФФЕРЕНЦИАЛА БЫЛИ ОДИНАКОВЫМИ.
Очень часто метод внесения под знак дифференциала используют для нахождения интегралов вида
∫ ( + ) = |
|
∫ ( + ) ( + ) = |
|
( |
) |
, где k – |
|
|
+ |
|
|
+ |
|
константа при x, F – первообразная функции f. Поэтому имеют место следующие формулы для неопределенных интегралов:
Пример 5
Найти интеграл  Внесем косинус под знак дифференциала
Внесем косинус под знак дифференциала
Пример 6
Найти неопределенный интеграл  Разложим тангенс, как отношение синуса и косинуса, затем внесем синус под знак дифференциала
Разложим тангенс, как отношение синуса и косинуса, затем внесем синус под знак дифференциала
Пример 7
Вычислить неопределенный интеграл  Внесем под знак интеграла
Внесем под знак интеграла  так, чтобы полученный многочлен под знаком интеграла совпадал со знаменателем
так, чтобы полученный многочлен под знаком интеграла совпадал со знаменателем
В результате, получили табличный интеграл , который в свою очередь равен
Пример 8
Вычислить неопределенный интеграл 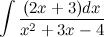
Так как  , то числитель можно внести под знак интеграла так, чтобы под дифференциалом образовался многочлен точно такой же, что и в знаменателе:
, то числитель можно внести под знак интеграла так, чтобы под дифференциалом образовался многочлен точно такой же, что и в знаменателе:
Полученный интеграл можно вычислить, используя табличный интеграл
Тогда искомый интеграл равен
Пример 9
Вычислить неопределенный интеграл  Используя формулу производной экспоненциальной функции внесем
Используя формулу производной экспоненциальной функции внесем 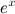 под знак дифференциала
под знак дифференциала
тогда в результате получим
Пример 10
Вычислить неопределенный интеграл 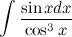 Используя формулу производной косинуса внесем
Используя формулу производной косинуса внесем  под знак дифференциала, а косинус поднимем в числитель:
под знак дифференциала, а косинус поднимем в числитель:
Пример 11
Вычислить неопределенный интеграл  Преобразуем подынтегральную функцию, используя равенство
Преобразуем подынтегральную функцию, используя равенство  , в результате получим:
, в результате получим:
Пример 12
Вычислить неопределенный интеграл  Используя формулу квадрата разности выделим в знаменателе подынтегрального выражения полный квадрат
Используя формулу квадрата разности выделим в знаменателе подынтегрального выражения полный квадрат
Внесем под знак дифференциала  :
:
Далее, используя табличный интеграл
получим
Пример 13
Вычислить неопределенный интеграл 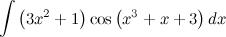
Так как  , то выражение перед косинусом можно внести под знак дифференциала
, то выражение перед косинусом можно внести под знак дифференциала
тогда будем иметь:
Пример 14
Вычислить неопределенный интеграл  Используя формулу производной косинуса внесем
Используя формулу производной косинуса внесем  под знак дифференциала
под знак дифференциала
Далее, используя табличный интеграл для показательной функции, получим
Еще примеры:



 Преобразуем заданный интеграл используя
Преобразуем заданный интеграл используя  :
:
 Внесем косинус под знак дифференциала
Внесем косинус под знак дифференциала Разложим
Разложим  Внесем под знак интеграла
Внесем под знак интеграла  так, чтобы полученный многочлен под знаком интеграла совпадал со знаменателем
так, чтобы полученный многочлен под знаком интеграла совпадал со знаменателем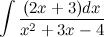
 , то числитель можно внести под знак интеграла так, чтобы под дифференциалом образовался многочлен точно такой же, что и в знаменателе:
, то числитель можно внести под знак интеграла так, чтобы под дифференциалом образовался многочлен точно такой же, что и в знаменателе:
 Используя формулу
Используя формулу 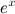 под знак дифференциала
под знак дифференциала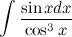 Используя формулу
Используя формулу  под знак дифференциала, а косинус поднимем в числитель:
под знак дифференциала, а косинус поднимем в числитель: Преобразуем подынтегральную функцию, используя равенство
Преобразуем подынтегральную функцию, используя равенство  , в результате получим:
, в результате получим:
 Используя формулу
Используя формулу  :
: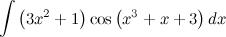
 , то выражение перед косинусом можно внести под знак дифференциала
, то выражение перед косинусом можно внести под знак дифференциала Используя формулу
Используя формулу  под знак дифференциала
под знак дифференциала