Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежская государственная лесотехническая академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

4718

.pdf

Скачиваний:

Добавлен:

08.01.2021

Размер:

1.47 Mб

Скачать

☆

1 / 51 2 3 4 5 > Следующая >>>

Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Воронежская государственная лесотехническая академия»

МАТЕМАТИЧЕСКИЙ АНАЛИЗ Линейная алгебра

Методические указания к выполнению контрольных работ для студентов 1 курса заочной формы обучения по направлению подготовки 080100 – Экономика

Воронеж 2012

УДК 517.1+512

Уточкина, Е. О. Математический анализ. Линейная алгебра [Текст] : методические указания к выполнению контрольных работ для студентов 1 курса заочной формы обучения по направлению подготовки 080100 – Экономика / Е. О. Уточкина, В. В. Зенина ; М-во образования и науки РФ, ФГБОУ ВПО «ВГЛТА». – Воронеж, 2012. – 44 с.

Печатается по решению учебно-методического совета ФГБОУ ВПО «ВГЛТА» (протокол № 7 от 25 мая 2012 г.)

Рецензент заведующий кафедрой математического моделирования ВГУ д-р физ.-мат. наук, проф. В.А. Костин

ВВЕДЕНИЕ

Данные методические указания и контрольные задания соответствуют образовательным стандартам Российской Федерации и рабочим программам по математическому анализу и линейной алгебре для студентов заочной формы обучения по направлению подготовки 080100 – Экономика, профиль – Бухгалтерский учет, анализ и аудит. В них включены как основные разделы дисциплин, так и те разделы, которые вынесены на самостоятельное изучение студентами.

Образцы выполнения заданий, включенные в контрольные работы по математическому анализу и линейной алгебре, содержат весь необходимый теоретический и практический материалы для самостоятельного решения студентами вариантов контрольных работ по этим дисциплинам.

При оформлении контрольной работы студенту необходимо учесть следующее:

1)на обложке тетради написать разборчиво свою фамилию, имя, отчество, шифр, номер контрольной работы и дату отправления работы в академию;

2)номера задач, входящих в контрольную работу, определяются по последней цифре шифра. Например, студент, имеющий шифр 12ЗЭ115, выполняет 5-й вариант, т.е. задачи 5, 15, 25, 35 и т.д. Работа, выполненная не по своему варианту, возвращается без рецензирования.

3)Каждая контрольная работа выполняется в отдельной тонкой тетради. Решения задач следует сопровождать объяснениями.

Если работа выполнена верно, то студент получает рецензию, в которой написано, что работа зачтена. Данную рецензию необходимо предъявить на экзамене или зачете.

При наличии ошибок контрольная работа не будет зачтена, в этом случае следует сделать исправления в этой же тетради и вернуть ее в академию вместе с рецензией.

Задачи, у которых номер заканчивается знаком *, приводятся с кратким решением.

Математический анализ

1семестр. Контрольная работа № 1: Х, 1Х, 2Х, 3Х, 4Х.

2семестр. Контрольная работа № 2: 5Х, 6Х, 7Х, 8Х, 9Х.

Линейная алгебра

2 семестр. Контрольная работа: 10Х, 11Х, 12Х, 13Х, 14Х.

МАТЕМАТИЧЕСКИЙ АНАЛИЗ

Контрольная работа № 1

0 – 9. Треугольник ABC задан координатами вершин. Найти:

1)длину стороны BC ;

2)уравнения сторон треугольника;

3)уравнение высоты, проведенной из вершины A ;

4)угол B в радианах с точностью до 0,01;

5)уравнение прямой, проходящей через вершину C параллельно прямой

AB .


Сделать чертеж.
0.	A( 3; 3),		B(	1; 6),		C( 6; 6) .
1.	A(	7; 3),	B( 5;		2),	C( 8; 2).
2.	A( 4;1),		B( 0; 2),			C( 5;10) .
3.	A( 7; 4),		B( 3;		7),	C( 2; 5) .
4.	A( 2;1),		B(	5; 8),		C( 7; 3).
5.	A(	3; 2),	B(	2; 5),		C( 6;1) .
6.	A( 5; 1),		B( 1;		4),	C( 4; 8).
7.	A(	8; 4),	B( 4;		1),	C( 7; 3).
8.	A(	14; 6), B(			2;1),	C( 1; 5) .
9.	A( 6; 0),		B( 2;		3),	C( 3; 9) .
*.	A(	6; 5),	B( 6; 0),			C( 9; 4) .
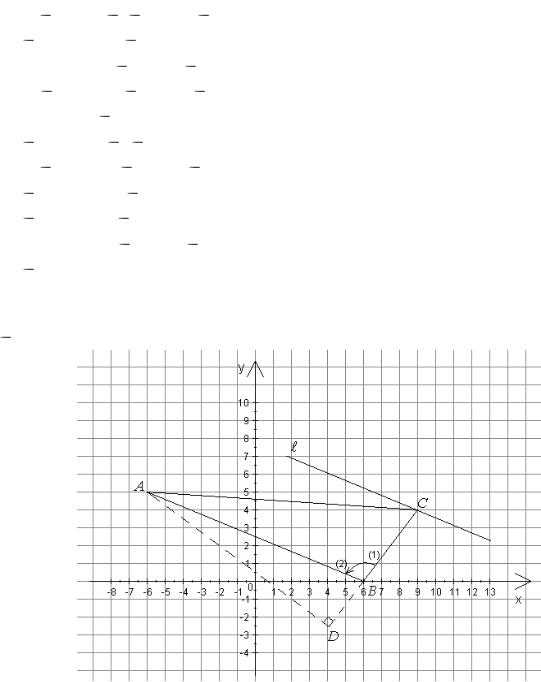
		Решение задачи *.
A(	6; 5), B( 6; 0),				C( 9; 4) .

Рис. 1

1)			Длину		стороны				ВС					найдем									по		формуле					расстояния		между			двумя
заданными точками M0 (x0 ; y0 ) и M1(x1; y1) :

									M			0	M		1						(x x )2						( y y		0	)2 .
									M				M								(x x )2						( y y			)2 .
																			1				0			1
Так как B( 6; 0) и C( 9; 4) , получаем

				6)2			0)2
	BC		(9	6)2	(4		0)2			9			16						25				5 .
		2) Для нахождения уравнений сторон треугольника, воспользуемся
уравнением				прямой,			проходящей												через						две		заданные точки					M0 (x0 ; y0 )				и
M1(x1; y1) :
																	y		y0					x	x0		.
																											.
																y1				y0				x1	x0
Так как A(				6; 5),		B( 6; 0) , то уравнение стороны АВ имеет вид																									y	5		x	(	6)	,
Так как A(				6; 5),		B( 6; 0) , то уравнение стороны АВ имеет вид																									0	5	6		(	6)	,
																															0	5	6		(	6)
или, после упрощения y										5			x				5	.
или, после упрощения y									12				x		2			.
									12						2
		Аналогично находим уравнения сторон BC и AC .
Уравнение BC :					y	0		x	6		или y									4		x	8.
Уравнение BC :					4	0	9		6		или y								3			x	8.
					4	0	9		6										3
Уравнение AC :					y	5		x	(	6)				или					y					1	x	23		.
Уравнение AC :					4	5	9		(	6)				или					y				15		x	5		.
					4	5	9		(	6)													15			5

3) Высота, проведенная из

вершины

A ,

есть

отрезок

прямой,

которая

перпендикулярна BC .

Уравнение высоты AD имеет вид:

x ) ,

где

( x ; y )

–

координаты

точки

A ;

–

угловой

коэффициент прямой

BC . Из полученного в пункте 2 уравнения

BC находим,

что

kBC

. По условию

6; 5)

, тогда

или

–

уравнение высоты AD .

Угол

B найдем по формуле

где

– угловые

коэффициенты прямых, образующих данный угол.

Из полученных в пункте 2 уравнений BC и AB находим, что

kAB

. Тогда

3,94 , а значит

(

)

Barctg( 3,94) 1,82(в радианах).

5)Уравнение прямой , проходящей через вершину C параллельно прямой AB имеет вид:

y y0

x0 ), где ( x0 ; y0 )

– координаты точки C ;

k – угловой коэффициент

прямой AB .

По

условию

C( 9; 4)

и kAB

тогда

y 4

(x 9)

или

– уравнение прямой .

10 – 19. Построить линии по заданным уравнениям.

10. a)

2)2

( y 3)2

б)

в)

11.a)

в)

12.a)

в)

13.a)

в)

14.a)

в)

15.a)

в)

16.a)

в)

17.a)

x2 y2

49 25

(x 3)2

x2 y2

25 16

(x 1)2

x2 y2

16 9

(x 3)2

x2 y2

64 25

(x 3)2

x2 y2

36 9

(x 2)2

x2 y2

16 4

(x 4)2

x2 y2

25 9

(x 4)2

1,			г)
( y	5)2	4,	б)
1,			г)
( y	2)2	16 ,	б)
1,			г)
( y	4)2	25 ,	б)
1,			г)
( y	3)2	4,	б)
1,			г)
( y	1)2	36 ,	б)
1,			г)
( y	2)2	49 ,	б)
1,			г)
( y	4)2	9,	б)

			y2			9x .
			x2					y2
													1			,
49				4									1			,
49				4
			y2			7x .
	x2					y2
										1					,
36				25						1					,
36				25
		y2			5x .
	x2					y2
									1,
25				16					1,
25				16
			y2					16x .
			x2					y2
													1			,
49				25									1			,
49				25
		y2						3x .
		x2						y2
												1,
												1,
9				4
		y2						2x .
		x2					y2
											1				,
											1				,
49				36
			y2			6x .
			x2					y2
														1		,
														1		,
36				9

										7
в)		x2		y2	1,					г) y2				x .
в)	36		16		1,					г) y2				x .
	36		16
18. a)	(x		5)2			( y	1)2	4 ,		б)		x2		y2	1,
18. a)	(x		5)2			( y	1)2	4 ,		б)					1,
										16			9
в)		x2		y2		1,				г) y2			8x .
в)	49		9			1,				г) y2			8x .
	49		9
19. a)	(x		5)2			( y	6)2	16	,	б)		x2		y2	1,
19. a)	(x		5)2			( y	6)2	16	,	б)					1,
										25			4
в)		x2		y2	1,					г) y2				9x .
в)	36		25		1,					г) y2				9x .
	36		25
1*. a) (x 1)2						( y 2)2		36	,	б)	x2			y2	1,
1*. a) (x 1)2						( y 2)2		36	,	б)					1,
										36			16
в)		x2		y2	1,					г) y2			4x .
в)	9		4		1,					г) y2			4x .
	9		4
	Решение задачи 1*
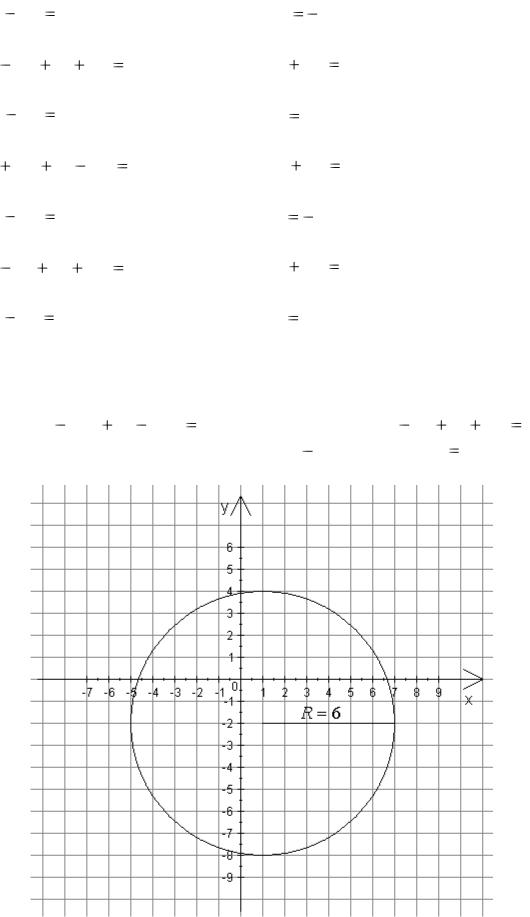
	а) Уравнение окружности с центром												в точке			C( x0; y0 )		и радиусом R
имеет		вид (x x )2						( y	y )2	R2 . Следовательно,						(x 1)2	( y	2)2 36 есть
							0		0
уравнение окружности с центром в точке C(1;														2) и радиусом R			6 (см. рис. 2).

Рис. 2

б)

Каноническим уравнением эллипса является уравнение

, при

этом

фокусы

эллипса находятся в

точках

F1 (

c; 0)

F2 ( c; 0) ,

где

b2 (a b) .

Следовательно,

есть

уравнение

эллипса с

полуосями a

6 и b

4 . Фокусы находятся в точках

F1 (

5; 0)

F2 ( 2

5; 0) .

Эллипс вписан в прямоугольник со сторонами x

6 ,

y 4 ,

4, центр

эллипса находится в начале координат (см. рис. 3).

Рис. 3

в)

Каноническим уравнением гиперболы является уравнение

при

этом

фокусы

гиперболы

находятся

точках

F1 (

c; 0)

и F2 ( c; 0) ,

где

. Следовательно,

1 есть уравнение гиперболы с полуосями

3 и b

2 . Фокусы находятся в точках F1 (

13; 0) и F2 (

13; 0) . Асимптотами

гиперболы

являются прямые

то

есть

x ,

которые

можно

построить

как

продолжение диагоналей

прямоугольника

со

сторонами

3 ,

2 ,

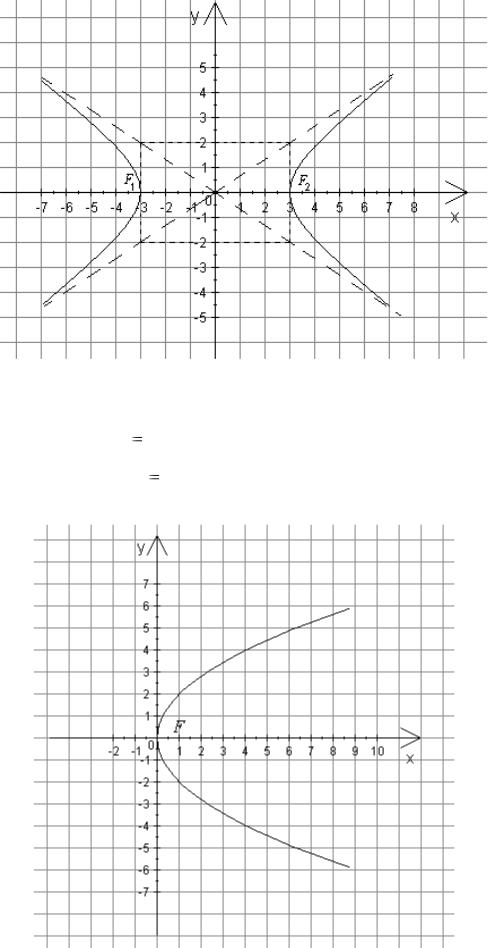
2. Центр гиперболы находится в начале координат (см. рис. 4).

						Рис. 4
		г)	Каноническим уравнением параболы, симметричной относительно оси
Ox ,		является уравнение		y2	2 px,	при этом фокус параболы находится в точке
F (	p	; 0) .	Следовательно,	y2	4x	есть уравнение параболы, фокус которой

2

находится в точке F(1; 0) (см. рис. 5).

Рис. 5

20 – 29. Вычислить пределы, не пользуясь правилом Лопиталя

20.

а) lim

3x2

7x 20

б) lim

2 5

в)

21.

а)

lim

б) lim

2x3

в)

3x2

11x 20

7x5

22.

а)

lim

б) lim

2x2

в)

3x 4

10 x2 x

23.

а) lim

б) lim

4x5

в)

7x 10

5 7x x5

x 5

24.

а)

lim

2x 8

б) lim

4x2

5x 10

в)

3x 4

2x3

3x 11x2

25.

а)

lim

6x 8

б) lim

2x2

4x 1

в)

26.

а) lim

2x 1

б) lim

3x4

в)

x 1 3x2

4x 1

3x 2

27.

а) lim

2x2

б) lim

2x3

в)

7x 6

4x5

x 1

x 6

28.

а) lim

7x 12

б) lim

4x2

7x 1

в)

29.

а) lim

б) lim

в)

3x 2

2 x 3x2

x 1

2*. а) lim

2x2

5x 7

б) lim

7x3

2x2

в)

Решение задачи 2*.

lim

cos 5x

x 0

lim

cos 3x

x 0

lim

sin 2x

x 0

tg3x

lim

tg 2x

x 0 sin 3x

lim

1 cos 5x

x 0

cos 3x

lim

sin 7x

x 0

tg5x

lim

cos 4x

x 0

lim

cos x

x 0

lim

2x2

cos 4x

x 0

lim

sin 6x

x 0

tg 4x

lim

cos 6x

x 0

а) lim		2x2		5x 7		2 12	5 1			7	0
а) lim		x	2	1	2		1				0
			2		2
x	1				1
x	1
Получили	неопределенность							0	.	Для		раскрытия этой неопределенности
Получили	неопределенность						0		.	Для		раскрытия этой неопределенности
							0

необходимо, воспользовавшись формулами сокращенного умножения, разложить числитель и знаменатель дроби на множители, а затем сократить дробь на общий множитель, дающий в пределе ноль.

Для числителя воспользуемся формулой разложения квадратного трехчлена

на множители a x2		b x c a (x x ) (x	x ) , где	x	и x – корни квадратного
		1	2	1	2
трѐхчлена. Получаем, что
2x2 5x	7 0
D b2	4 a c 52	4 2 ( 7) 25 56 81

1 / 51 2 3 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
08.01.20211.46 Mб24713.pdf
#
08.01.20211.46 Mб14714.pdf
#
08.01.20211.47 Mб24715.pdf
#
08.01.20211.47 Mб64716.pdf
#
08.01.20211.47 Mб24717.pdf
#
08.01.20211.47 Mб14718.pdf
#
08.01.2021201.56 Кб1472.pdf
#
08.01.20211.48 Mб14720.pdf
#
08.01.20211.48 Mб24721.pdf
#
08.01.20211.48 Mб14722.pdf
#
08.01.20211.48 Mб44723.pdf