Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежская государственная лесотехническая академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

4718

.pdf

Скачиваний:

Добавлен:

08.01.2021

Размер:

1.47 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

11*. а)

б)

Решение задачи 11*

а)

Определителем второго порядка

называется

число,

полученное с

помощью элементов квадратной матрицы

a11

a12

2-го порядка следующим

a21

a22

образом:

a11

a12

a11

a22

a21

a12 .

a21

a22

Тогда

4 5

2 (

б)

1 способ – правило Саррюса.

a11

a12

a13

определителю

третьего

порядка

a21

a22

a23

справа

приписываются

a31

a32

a33

a11

a12

a13

a11

a12

первый и второй столбцы

a21

a22

a23

a21

a22 . Затем элементы, стоящие на

a31

a32

a33

a31

a32

диагоналях полученной таблицы, перемножаются, и эти произведения складываются, причем произведения элементов на диагоналях, идущих снизу вверх, берутся со знаком минус:

						a11	a12	a13	a11	a12
						a11	a12	a13	a11	a12
						a21	a22	a23	a21	a22
						a31	a32	a33	a31	a32
	a11 a22 a33		a12	a23 a31	a13		a21 a32 a31		a22	a13 a32 a23 a11 a33 a21 a12 .
	Имеем
3	2	2		2	2		3	2
3	2	2	3	2	2		3	2
1	3	2	1	3	2		1	3 3 ( 3) 3 2 ( 2) 2 2 1 4
2	4	3	2	4	3		2	4

2 ( 3) 2 4 ( 2) 3 3 12 27 8 8 12 24 6 3.

2 способ – разложение по элементам строки или столбца.

Минором элемента определителя называется определитель, полученный из данного путем вычеркивания строки и столбца, на пересечении которых стоит выбранный элемент.

Обозначение: aij

– выбранный элемент определителя, M ij

– его минор.

Алгебраическим дополнением Aij элемента определителя называется его

минор M

, взятый со знаком (

1)i j , то есть A

( 1)i j M

Например,

рассмотрим

определитель

третьего

порядка

Найдем минор и алгебраическое дополнение элемента

a21 5.

Минор будет

равен определителю второго порядка, полученному из исходного вычеркиванием второй строки и первого столбца, на пересечении которых расположен элемент

a21 5:
M			3	2 4 ( 1) 3 8 3 11 .
		2	3
	21	1	4
		1	4

Алгебраическое дополнение элемента a21 равно:

A ( 1)2 1	M	21	( 1) 11 11.
21		21

Справедливо следующее утверждение: определитель равен сумме произведений элементов любой его строки или столбца на их алгебраические дополнения.

a11 a12 a13

Для примера рассмотрим определитель третьего порядка a21 a22 a23 и

a31 a32 a33

разложим его по элементам первого столбца:

a11	a12	a13
a21	a22	a23	a11 A11 a21 A21 a31 A31.
a31	a32	a33

При вычислении часто используется следующее свойство определителей: величина определителя не изменится, если к элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.

3 2 2

Рассмотрим заданный определитель 1

2 .

2 4 3

Умножим элементы второй строки на ( 3) и сложим с соответствующими элементами первой строки, а затем элементы второй строки умножим на ( 2) и

сложим с соответствующими элементами третьей строки и разложим полученный определитель по первому столбцу.

Имеем

	3	2		2		3 1 ( 3)			2 ( 3) ( 3) 2 ( 2) ( 3)									0 11		8
	1	3		2		1				3				2				1	3	2
	2	4		3		2 1 ( 2)			4 ( 3) ( 2) 3 ( 2) ( 2)									0 10		7
0		A	1 A			0 A	0	1 (	1)2 1	M	21	0	1 (	1)3			8	1 (11 7		10 8) 3
0		A	1 A			0 A	0	1 (	1)2 1	M		0	1 (	1)3		11	8	1 (11 7		10 8) 3
		11		21	31											10	7
																10	7
120 – 129. Найти обратную матрицу A 1 к заданной матрице A .
120.		A		2	6 .						125.		A	3	6 .
				4	11									9	19
121.		A		2	4 .						126.		A	3	6 .
				6	13									2	5
122.		A		2	8 .						127.		A	4	8 .
				6	23									2	3
123.		A	2		6 .						128.		A	4	12 .
			10		31									2	5
124.		A	3		9 .						129.		A	4	16 .
			6	17										2	7
12*. A				5	10 .
				2	3
		Решение			задачи		12*. Матрица					A 1	называется				обратной		к квадратной
матрице			A ,	если A A 1				A 1	A	E ,	где		E –	единичная				матрица,		у которой

элементы, расположенные на главной диагонали, равны 1, а остальные – нулю. Для того, чтобы матрица A имела обратную необходимо и достаточно,

чтобы ее определитель был отличен от нуля, то есть

Алгоритм нахождения обратной матрицы:

найти

A ;

если

0, то обратная матрица не существует;

если

0, то к исходной матрице

a11

a12

справа приписываем

a21

a22

единичную матрицу

и путем элементарных преобразований расширенную

a11

a12

матрицу

приводят к виду

a11

a12

;

a21

a22

a21

a22

				~	~
4)	обратная матрица имеет вид	A	1	a11	a12	;
4)	обратная матрица имеет вид	A		~	~	;
				a21	a22
5)	сделать проверку A A 1 A 1 A			E .

Замечание. Следующие преобразования строк матрицы:

–умножение любой строки на число, отличное от нуля;

–прибавление к строке другой строки, умноженной на любое число;

–перестановка строк;

–отбрасывание нулевой строки

называются элементарными.

Применим этот алгоритм к нахождению обратной матрицы для заданной

матрицы A	5	10 .
	2	3

Сначала убедимся в том, что обратная матрица существует. Для этого вычислим определитель исходной матрицы

5	10	5 ( 3) 2 ( 10)	15 20 5 0.
2	3	5 ( 3) 2 ( 10)	15 20 5 0.
2	3

Следовательно, обратная матрица существует. Для ее нахождения расширенную


матрицу	5		10		1	0	путем элементарных преобразований приведем

	2		3		0	1

	1	0		~	~

к виду				a11	a12	. Сначала разделим первую строку расширенной
				~	~
	0	1		a21	a22

матрицы на 5, затем умножим ее на ( 2) и сложим с соответствующими

элементами второй строки. Вторую строку полученной матрицы умножим на 2 и прибавим к элементам первой строки. Имеем

5		10	1	0		1	2				0	1	2		1	0
									1
									1
										5					5
										5					5
2		3	0	1		2	3			0	1	0	1		2	1
	1	0			2										5

			3
			5
			5			.
			2			.
	0	1	2		1
	0	1	5		1
			5
							3			2
Тогда обратная матрица A						1	5			2	.
						1	5
							2			1
							2
							5
							5
Сделаем проверку A A 1						A 1	A	E .
		5	10	3			2		5		3	( 10)	2	5 2		( 10) 1
A A	1	5	10		5		2		5		5	( 10)	5	5 2		( 10) 1
	1				5						5		5
		2	3	2			1			2	3	( 3)	2	2 2 ( 3) 1
		2	3	2	5		1			2	3	( 3)	2	2 2 ( 3) 1
					5						5		5

								35
	1		0	E .
	0		1	E .
	0		1
				3	2	5	10	3		5	2 2	3		(	10)	2 (	3)
A	1	A		5	2	5	10	5		5	2 2	5		(	10)	2 (	3)
	1			5				5				5
				2	1	2	3	2		5	1 2	2		(	10)	1 (	3)
				2		2	3	2	5			2	5
				5					5				5
	1		0	E .
	0		1	E .
	0		1

130 – 139. Решить систему линейных алгебраических уравнений методом Крамера.

	3x 4 y 3z			2		2x 5y z 1
130.	x	3y	z	1	135.	3x	2 y			3z	1
	2x 2 y 3z			1		x 3y 2z 2
	2x 3y 3z			1		3x 2 y 4z					1
131.	3x	y	4z	1	136.	2x	3y		3z		1
	x	3y	z	1		x	y	3z			2
	3x y 3z			1		3x 4 y 2z 3
132.	x	3y	3z	1	137.	2x	y		z	1
	2x y 2z 1					4x 3y 2z 3
	3x 2 y 3z 2					2x y 3z 1
133.	2x	y	z	1	138.	3x	2 y			2z	1
	x	2 y	z 0			x	y	3z		2
	2x 3y 4z 3					2x y 5z 1
134.	x	3y	2z	4	139.	x	3y		4z		1
	3x y 5z 3					2x y z 1
	3x 2 y 2z 1
13*. x 2 y			2z	1
	2x	y	3z	1

Решение задачи 13*. Рассмотрим систему линейных алгебраических

a11x a12 y a13z b1

a11 a12 a13

уравнений a21x a22 y a23z b2 . Определитель a21 a22 a23 , элементами

a31x a32 y a33z b3

a31 a32 a33

которого являются коэффициенты при неизвестных, называется главным определителем системы. Если главный определитель системы линейных алгебраических уравнений отличен от нуля ( 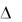0 ), то система имеет единственное решение, которое может быть найдено по формулам Крамера

x x , y y , z z ,

где x , y , z – вспомогательные определители системы, которые получаются из

главного определителя 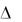путем замены соответствующего столбца на столбец из правых частей уравнений системы:

a12

a13

a11

a13

a11

a12

a22

a23

a21

a23

a21

a22

a32

a33

a31

a33

a31

a32

2 y

Вычислим главный определитель системы x									2 y	2z	1.
								2x	y	3z	1
3	2	2		2	2	3	2
3	2	2	3	2	2	3	2
1	2	2	1	2	2	1	2	3 2 3 2 ( 2) 2 ( 2) 1 ( 1)
2	1	3	2	1	3	2	1

22 ( 2) ( 1) ( 2) 3 3 1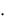2 18 8 2 8 6 6 8

Так как 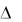8 0 , то система имеет единственное решение, которое может быть найдено по формулам Крамера. Составим и вычислим вспомогательные определители:

1	2	2		2	2	1	2
1	2	2	1	2	2	1	2
1	2	2	1	2	2	1	2	1 2 3 2 ( 2) 1 ( 2) ( 1) ( 1)
1	1	3	1	1	3	1	1

1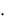2 ( 2) ( 1) ( 2) 1 3 ( 1) 2 6 4 2 4 2 6 8 ;

	3		1	2				3	1	2			3			1
	3		1	2				3	1	2			3			1
y	1		1	2				1	1	2			1			1 3 ( 1) 3 1 ( 2) 2 ( 2) 1 1
y
	2		1	3				2	1	3			2			1
2 ( 1) ( 2) 1 ( 2) 3 3 1 1 9 4 2 4 6 3																			16;
	3		2	1					2	1		3			2
	3		2	1		3			2	1		3			2
z	1 2			1		1 2				1		1 2				3 2 1 2 ( 1) 2 1 1 ( 1)
z
	2		1	1		2			1	1		2			1
2 2 1 ( 1) ( 1) 3 1 1 2 6 4 1 4 3 2																	8.
	Тогда x				x		8	1,	y		y			16		2,	z	z		8	1.
	Тогда x					8		1,	y			8				2,	z		8		1.
						8						8							8
Сделаем проверку:
3 1 2 ( 2) 2 ( 1) 1												1 1
1 2	(	2)	2 (	1)		1			;			1				1		верно.
2 1	(	2)	3 (	1)		1						1			1

Таким образом, система имеет единственное решение x 1,		y 2,	z 1.
140 – 149. Пирамида ABCD задана координатами		вершин.	Пользуясь
понятиями и формулами векторной алгебры, найти:
1)	длину ребра AB ;
2)	угол между ребрами AB и AD ;
3)	площадь грани ABC ;
4)	объем пирамиды.

20.A(7;5;3) , B(9;4;4) , C(4;5;7) , D(7;9;6) .

21.A(6;1;1), B(4;6;6) , C(4;2;0) , D(1;2;6) .

22.A(5;5;4) , B(3;8;4) , C(3;5;10) , D(5;8;2) .

23.A(0;7;1) , B(4;1;5) , C(4;6;3) , D(3;9;8) .

24.A(9;5;5) , B( 3;7;1), C(5;7;8) , D(6;9;2) .

25.A(2;4;3) , B(7;6;3) , C(4;9;3) , D(3;6;7).

26.A(3;5;4) , B(5;8;3) , C(1;9;9) , D(6;4;8).

27.A(3;3;9) , B(6;9;1) , C(1;7;3) , D(8;5;8) .

28.A(3;1;4) , B( 1;6;1) , C( 1;1;6) , D(0;4; 1) .

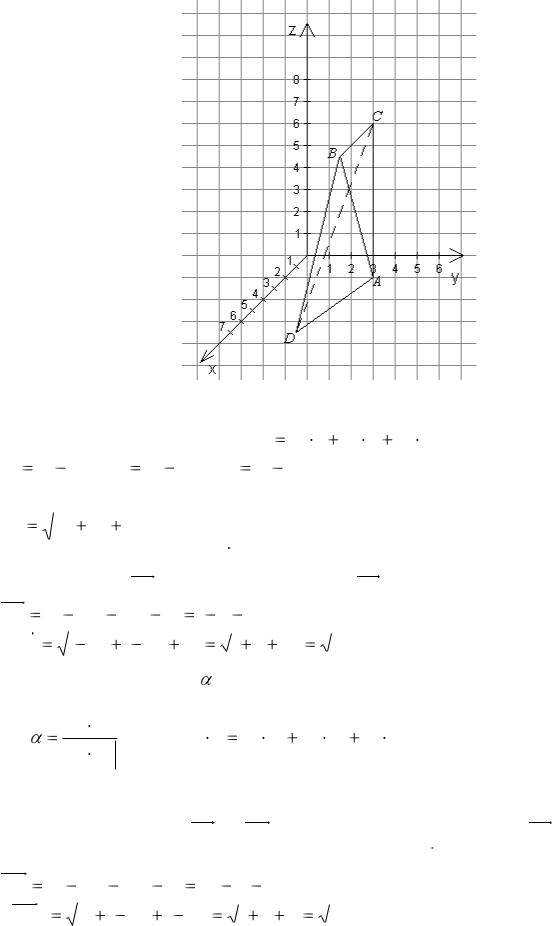
29.A(6;6;7) , B(5;7;8) , C(2;2;2), D(2;5;4) . 2*. A(6;6;2) , B(5;4;7) , C(2;4;7), D(7;3;0).

Решение задачи 2*.

Рис. 8

Координаты

вектора

находятся

по

формулам:

ax i

x0 ,

y0 ,

z0 ,

где

(x0 ; y0 ; z0 )

– координаты

начала,

(x1; y1; z1)

–

координаты

конца

вектора

Тогда

длина вектора

равна

ax2

ay2

az2 .

Рассмотрим вектор AB. Точка A(6;6;2) является началом, а точка B(5;4;7) –

концом вектора AB. Следовательно, вектор AB имеет следующие координаты:

6; 4

6; 7

{

2; 5}, а значит

(

1)2

(

2)2

30 .

Косинус

угла

между

векторами

может быть найден по

и b

формуле:

a b

cos

где

a b

ax bx ay

–

скалярное

произведение

векторов a и b .

Для того, чтобы найти угол между

ребрами AB и AD , введем в

рассмотрение векторы AB и AD.

Так как координаты вектора AB и его длина

известны, определим координаты и длину вектора AD :

6; 3

6; 0

{1;

2},

( 3)2

( 2)2

1 9 4

14 .

								39
	Тогда
cos		AB AD (			1) 1 ( 2)	(	3)	5 ( 2)	5


		AB	AD		30		14		30	14
		AB	AD		30		14		30	14

или cos				5	0,24 . Отсюда			arccos(	0,24)		104 .



	2			105

3)Площадь треугольника, построенного на векторах a и b , находится по

							1
							1
формуле S										a	b		, через векторное произведение
формуле S								2		a	b		, через векторное произведение



				i				j		k

a b			ax ay							az		(aybz							azby ) i (axbz									azbx ) j (axby						aybx ) k .
			bx					by		bz
		Площадь грани														ABC				есть площадь треугольника														ABC ,		построенного на
векторах AB и AC . Так как AC																							{	4; 2; 5}, тогда


								i		j			k

AB		AC					1		2		5						(		10			10)		i	(		5	20)			j (2		8)	k 0 i 15			j	6k ,
							4		2		5
а значит
а значит
				1										1															1						1
S	ABC			1		AB			AC					1			02			(		15)2			(		6)2		1		225		36		1	261
S		2				AB			AC		2						02			(		15)2			(		6)2	2			225		36	2		261

	1							3

		9 29							29						8,1.

	2						2
	2						2
		4)			Объем V
		4)			Объем V							треугольной пирамиды, построенной на векторах a , b ,																											c
																			1
																			1
находится по формуле V																					(a		b )		c	.
находится по формуле V																			6		(a		b )		c	.
																			6		1
		В			нашем случае													V					( AB			AC)		AD		.		Так	как		AB	AC	{0;	15;	6},

																				6

AD {1; 3; 2}, получаем:

V	1			1	57		57	9,5 .
		0 1 ( 15) ( 3) ( 6) ( 2)
	6		6			6

Библиографический список

Основная литература

1.	Общий курс высшей математики для экономистов [Текст] : учеб.
пособие / под ред. В. И. Ермакова. – М. : ИНФРА-М, 2003. – 656 с.
2.	Высшая математика			для экономистов [Текст]		:	учеб.	/	под ред.
Н. Ш. Кремера. – М. : ЮНИТИ, 2008. – 479 с.
3.	Ильин, В. А.		Линейная алгебра		[Текст] : учеб.		/ В.	А. Ильин,
Э. Г. Позняк.– М. : ФИЗМАТЛИТ, 2007. – 280 с.
			Дополнительная литература
4.	Привалов,	И.	И.	Аналитическая	геометрия	[Текст]		:	учеб. /
И. И. Привалов. – СПб. ; М. ; Краснодар : Лань, 2007. – 304 с.
5.	Берман, Г.	Н.	Сборник задач по		курсу математического				анализа.

Решение типичных и трудных задач [Текст] : учеб. пособие / Г. Н. Берман. – 2-е изд. – СПб. : Лань-Трейд, 2007. – 608 с.

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
08.01.20211.46 Mб24713.pdf
#
08.01.20211.46 Mб14714.pdf
#
08.01.20211.47 Mб14715.pdf
#
08.01.20211.47 Mб64716.pdf
#
08.01.20211.47 Mб14717.pdf
#
08.01.20211.47 Mб14718.pdf
#
08.01.2021201.56 Кб1472.pdf
#
08.01.20211.48 Mб04720.pdf
#
08.01.20211.48 Mб24721.pdf
#
08.01.20211.48 Mб14722.pdf
#
08.01.20211.48 Mб34723.pdf

								35
	1		0	E .
	0		1	E .
	0		1
				3	2	5	10	3		5	2 2	3		(	10)	2 (	3)
A	1	A		5	2	5	10	5		5	2 2	5		(	10)	2 (	3)
	1			5				5				5
				2	1	2	3	2		5	1 2	2		(	10)	1 (	3)
				2		2	3	2	5			2	5
				5					5				5
	1		0	E .
	0		1	E .
	0		1

								35
	1		0	E .
	0		1	E .
	0		1
				3	2	5	10	3		5	2 2	3		(	10)	2 (	3)
A	1	A		5	2	5	10	5		5	2 2	5		(	10)	2 (	3)
	1			5				5				5
				2	1	2	3	2		5	1 2	2		(	10)	1 (	3)
				2		2	3	2	5			2	5
				5					5				5
	1		0	E .
	0		1	E .
	0		1

								35
	1		0	E .
	0		1	E .
	0		1
				3	2	5	10	3		5	2 2	3		(	10)	2 (	3)
A	1	A		5	2	5	10	5		5	2 2	5		(	10)	2 (	3)
	1			5				5				5
				2	1	2	3	2		5	1 2	2		(	10)	1 (	3)
				2		2	3	2	5			2	5
				5					5				5
	1		0	E .
	0		1	E .
	0		1