4412

Для ее доказательства предположим, что прямые u1 , u2 не являются перпендикулярными, и воспользуемся известной формулой тригонометрии,

следует, что k1 k2 .

Вывод: условием параллельности прямых служит равенство их угловых коэффициентов. Если прямые u1 , u2 перпендикулярны, то 2 , и формулой

(4.7) воспользоваться нельзя. Однако в этом случае можно рассматривать

33

Под расстоянием от точки M до прямой u понимается длина перпендикуляра d , опущенного из

коэффициенты. Для этого разделим каждое из них на коэффициенты при

34

Это и есть расстояние от точки M x0 , y0 до прямой Ax By C 0 .

Аналитическая геометрия в пространстве Плоскость. Уравнение плоскости, проходящей через данную точку

Рассмотрим в пространстве плоскость П. Положение ее вполне определяется заданием вектора p , перпендикулярного этой плоскости и некоторой фиксированной точки M 0 x0 , y0 , z0 , лежащей в плоскости П.

Вектор p , перпендикулярный плоскости, называется нормальным вектором этой плоскости ( p 0 ). Будем предполагать, что нормальный вектор p имеет координаты A, B, C : ь p A, B, C 0 .

совпадают с координатами конца M 0 этого вектора, следовательно, r0 x0 , y0 ,z0 .

35

Рис.4.5

Уравнение (4.20) называется векторным уравнением плоскости П.

Выражая скалярное произведение векторов через их проекции, получим уравнение той же плоскости П в координатной форме:

Уравнение (4.10) называется общим уравнением плоскости (ортогональной вектору p A, B, C 0 ).

Прямая линия в пространстве. Уравнение прямой линии

Пусть требуется найти уравнение прямой линии, проходящей через точку

M0 x0 , y0 , z0 .

Чтобы задать прямую линию, нужно знать так называемый направляющий вектор прямой.

Определение. Направляющим вектором прямой называется любой ненулевой вектор, которому прямая параллельна.

Будем предполагать, что направляющий вектор a прямой u имеет компоненты l , m, n : a l , m, n 0 .

Обозначим через r0 радиус-вектор,

проведенный в точку M 0 , и заметим, что он имеет вид r0 x0 , y0 ,z0 .

36

Уравнение, в котором скаляр t играет роль переменного параметра,

называется векторным уравнением прямой линии.

Если записать векторное уравнение прямой линии в проекциях, то получим

параметрическими уравнениями прямой линии.

Наряду с параметрическими уравнениями прямой линии, представляющими собой 3 уравнения с 4 неизвестными t, x, y, z , нередко определяют прямую линию посредством системы уравнений первой степени между текущими

каноническими уравнениями прямой линии, проходящей через точку

M0 x0 , y0 , z0 параллельно вектору a l , m, n .

Замечание 1.6. В последних уравнениях все числа l, m, n одновременно не могут обратиться в ноль, так как a 0 . Но некоторые из них могут равняться нулю. В этом случае будем считать, что соответствующий числитель также равен нулю.

Угол между двумя прямыми линиями

Определение. Углом между прямыми u1 , u2 в пространстве

называется любой из углов, образованных двумя прямыми, проведенными через произвольную общую точку параллельно данным прямым. Легко видеть,

что 0 .

Вычисление cos . Пусть обе прямые u1 , u2 заданы каноническими

37

В последней формуле можно ставить любой знак в зависимости от выбора одного из двух различных углов между прямыми u1 , u2 .

5. КРИВЫЕ ВТОРОГО ПОРЯДКА

Определение. Кривой второго порядка называется линия, определяемая уравнением второй степени относительно текущих декартовых координат.

В общем случае это уравнение имеет следующий вид:

Ax2 2Bxy Cy2 2Dx 2Ey F 0 ,

где коэффициенты A, B, C, D, E, F – действительные числа и, кроме того, по крайней мере одно из чисел A, B или C отлично от нуля.

Различают 4 типа кривых второго порядка:

1) эллиптический; 2) гиперболический; 3) параболический; 4) вырожденный. Ниже будут получены следующие канонические (простейшие, принятые за

образец) уравнения:

К вырожденному типу относится каждое из следующих уравнений: x2 a2 0 пара вертикальных прямых;

y2 b2 0 пара горизонтальных прямых;

a2 y2 b2 x2 0 пара пересекающихся прямых; a2 x2 b2 y2 0 точка О(0;0);

a2 x2 b2 y2 1 пустое множество.

Напомним формулу для вычисления расстояния между двумя точками:

38

если имеются две точки M x1; y1 и N x2; y2 , то расстояние между ними вычисляется по формуле MN x2 x1 2 y2 y1 2 .

(множество всевозможных точек) плоскости, сумма расстояний от каждой из которых до фокусов является постоянной величиной 2a , превышающей расстояние между фокусами 2c .

Обозначим произвольную точку эллипса через M x; y . Согласно определению эллипса

MF1 MF2 2a .

Рис. 5.1

Поскольку

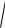MF1 x c 2 y 0 2 x c 2 y2 , MF2 x c 2 y 0 2 x c 2 y2 ,

то уравнение эллипса принимает вид

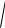x c 2 y2 x c 2 y2 2a . (5.1)

Далее будем преобразовывать эту формулу, чтобы в результате прийти к каноническому уравнению эллипса.

39

По существу, в уравнении (5.1) осталось избавиться от иррациональности, а это осуществляется, как известно, возведением в квадрат обеих частей

Разделив обе части полученного равенства на произведение a2b2 , приходим

Следует заметить, что в определении эллипса фигурируют два числа a, c, а в каноническом уравнении появляется b, связанное с ними по формуле (5.3).

Найдем точки пересечения эллипса с осями координат: если положить x 0 в (3.5), то y b , если в (5.5) положить y 0, то x a .

40

Определение. Число а называется большой полуосью эллипса, а число b – его малой полуосью.

Нетрудно видеть, что эллипс представляет собой кривую, симметричную относительно координатных осей и начала координат.

Определение. Эксцентриситетом эллипса называется отношение фокусного

расстояния с к большей полуоси а, т.е. ac .

Из (5.2) вытекает, что для эллипса 1.

Частный случай. Если a b , то c 0 , оба фокуса совпадают и образуют центр O(0, 0), а уравнение соответствующей кривой принимает вид

x2 y2 a2 .

Мы видим, что получено уравнение окружности радиуса а с центром в начале координат, причем эксцентриситет окружности 0 , так как c 0 .

Гипербола, ее каноническое уравнение

Пусть снова имеются точки F1 c;0 и F2 c;0 , c 0 , называемые фокусами. Определение. Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний от каждой из которых до фокусов

Далее приведем полученное уравнение к каноническому виду. С этой целью возведем дважды обе части равенства (5.6) в квадрат.

41

и возведем в квадрат обе части равенства (5.6), получим уравнение z 2cx 2 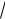z 2cx z 2cx z 2cx 4a2 ,

Или 2z 2 z2 4c2 x2 4a2 , которое запишем таким образом:

z2 4c2 x2 z 2a2 .

После возведения в квадрат обеих частей последнего равенства получаем z2 4c2 x2 z2 4a2 z 4a4 ,

Заметим, что в определении гиперболы также фигурируют два числа a, c, а в каноническом уравнении появляется b, связанное с ними по формуле (5.8).

Найдем точки пересечения гиперболы (5.10) с осями координат: если x 0 , то приходим к невозможному равенству y2 b2 , если y 0, то x a .

Определение. Число а называется действительной полуосью гиперболы, а число b – ее мнимой полуосью.

42