4412

Выберем в R3 произвольную точку M и построим вектор OM . Так как векторы i , j , k образуют базис, то вектор OM можно разложить на компоненты по этому базису: OM 1i 2 j 3 k ,

где 1 , 2 , 3 – координаты вектора OM в заданном базисе.

Проведем через точку O в направлении векторов i , j , k оси Ох, Оу, Оz соответственно и

спроектируем вектор OM на каждую из осей

(рис. 2.15).

Пусть точки M1, M 2 , M3 есть проекции точки M на оси абсцисс, ординат и аппликат соответственно.

Тогда

OM OM1 OM 2 OM3

ПрOx OM i ПрOy OM j ПрOz OM k .

Координаты вектора OM определяются по формулам

1 ПрOx OM , 2 ПрOy OM , 3 ПрOz OM .

В прямоугольной декартовой системе эти координаты принято обозначать через x, y, z соответственно и называть прямоугольными декартовыми координатами вектора OM или декартовыми координатами точки M R3 .

Итак, OM 1i 2 j 3 k xi y j zk x; y; z .

Координаты точки M R3 записываются в форме M(x; y; z). Пусть вектор a OM задан в координатной форме a x; y; z . Так как этот вектор совпадает с диагональю прямоугольного параллелепипеда (рис.2.15), то его длина равна

23

Рис. 2.16.

Тогда OM1 x1; y1; z1 , OM 2 x2; y2 ; z2 , M1M2 OM 2 OM1

иM1M2 x2 x1 i y2 y1 j z2 z1 k .

Так как длина вектора M1M 2 равна расстоянию между точками M1 и M 2 , то

d M1M 2 x2 x1 2 y2 y1 2 z2 z1 2 .

Заметим, что в процессе решения этой задачи установлена формула определения координат вектора, если заданы координаты его начальной и конечной точек: M1M2 x2 x1 i y2 y1 j z2 z1 k .

Скалярное произведение векторов

Пусть даны два вектора a и b . В векторной алгебре рассматриваются два вида умножения векторов: скалярное, результатом которого является число, и векторное, результатом которого является вектор.

Определение. Скалярным произведением векторов a и b называется число, равное произведению модулей перемножаемых векторов на косинус угла между ними (рис. 2.17). Скалярное произведение обозначается

символом ab . Итак, ab ab cos .

25

Рис. 2.17.

откуда следует, что скалярное произведение векторов a и b равно модулю одного из векторов, умноженному на проекцию другого на направление первого вектора.

Свойства скалярного произведения векторов

1)ab ba ;

2)ab 0 , если a b или хотя бы один из векторов есть нулевой вектор (справедливо и обратное утверждение);

3)aa a 2 ;

Найдем скалярное произведение ab . Вычислим предварительно скалярные

перпендикулярны. Тогда, согласно свойству 2, их произведения друг на друга равны нулю.

Последнее называется условием перпендикулярности двух векторов.

26

Векторное произведение двух векторов

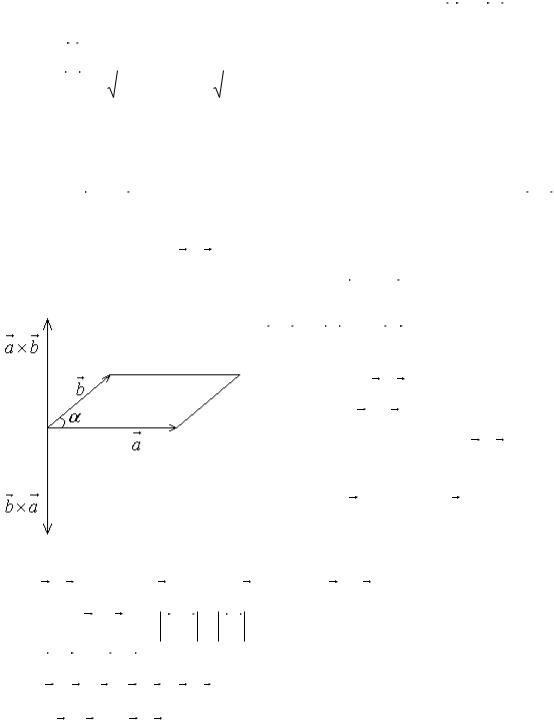
Определение. Векторным произведением ненулевых и неколлинеарных векторов a и b называется вектор, обозначаемый символом a b , который определяется следующими тремя условиями:

1) модуль вектора a b равен площади параллелограмма, построенного на

2) вектор a b перпендикулярен каждому из векторов a и b ;

3) направлен вектор a b так, что если смотреть из конца его, то кратчайший поворот от вектора a к вектору b производится против движения часовой стрелки.

Свойства векторного произведения

1.a b 0 , если a 0 , или b 0 , или a и b коллинеарны.

2.Если a b , то a b ab

3.a b b a

4.a b c a c b c

5.a b a b

Выражение векторного произведения двух векторов через координаты векторов сомножителей

27

Геометрический смысл модуля векторного произведения

a b S параллелограмма

12 a b S треугольника

Смешанное произведение векторов

Пусть даны три вектора a , b , c . Так как для векторов введены два вида произведений – скалярное и векторное, то для трех векторов относительно операции умножения существуют разные виды произведений.

Рассмотрим подробно произведение называемое смешанным. Это. произведение, в котором вначале находится векторное произведение двух из заданных векторов, а затем скалярное произведение полученного вектора на третий из данных векторов.

Например, вначале находится векторное произведение a b d , затем – скалярное произведение d c a b c .

Смешанное или иначе векторно-скалярное произведение обозначается символом a b c или символом abc . Результатом смешанного произведения является число.

Пусть требуется определить смешанное произведение векторов, если

28

Формула дает выражение для смешанного произведения в координатной форме. Заметим, что в этой формуле координаты векторов a , b , c записаны соответственно в первой, второй и третьей строках определителя.

Для смешанного произведения векторов справедливы равенства

a b с b c a c a b a c b c b a b a с .

Проверим, например, справедливость равенства a b с b a с . Согласно

срок определителя знак определителя меняется на противоположный. Тогда,

a b с равен объему параллелепипеда, построенного на этих векторах как на ребрах.

Следствие (условие компланарности трех векторов). Для того, чтобы три вектора a , b , c были компланарны, необходимо и достаточно, чтобы их

29

смешанное произведение равнялось нулю, т.е. a b с 0 или в координатной

Из школьного курса математики известно, что в декартовой системе

Первое равенство является уравнением вертикальной прямой линии, проходящей через точку A a,0 и параллельной оси Oy . Второе уравнение задает линейную функцию, графиком которой является невертикальная прямая. Напомним геометрический смысл параметров k и b , входящих в уравнение

(4.2).

Будем обозначать прямые строчными латинскими буквами (возможно с нижними индексами).

Определение. Углом наклона прямой u к оси Ox называется угол,

откладываемый против часовой стрелки от положительного направления оси Ox до прямой u : u,Ox , 0 .

Рис. 4.1

Определение. Угловым коэффициентом невертикальной прямой u

Теперь положим x 0 в уравнении (4.2), получим y b . Геометрически это означает, что число b – ордината точки пересечения прямой с осью Oy .

Определение. Уравнение прямой вида (4.2) называется уравнением прямой

arctg k .

Уравнение прямой, проходящей через данную точку в данном направлении

Пусть дана точка M x0 , y0 , а также дан угловой коэффициент k , определяющий направление прямой линии, проходящей через точку M .

Уравнение этой прямой записывается в виде y y0 k x x0 . (4.3)

В самом деле, если искать уравнение прямой в виде (4.2), то неизвестное число b следует определять из условия принадлежности точки M прямой.

Замечание 4.2. Направление прямой линии можно задать не только угловым коэффициентом k , но также ее углом наклона к оси Ox , и тогда в силу (4.4) уравнение прямой, проходящей через точку M x0 , y0 под углом к оси Ox , записывается в виде

y y0 tg x x0 . (4.4)

Уравнение прямой, проходящей через две данные точки

31

Пусть даны точки M x0 , y0 и N x1, y1 , не лежащие на вертикальной прямой, т.е. x0 x1 . Составим уравнение прямой, проходящей через эти точки. Оказывается, что уравнение этой прямой записывается в виде

Для доказательства воспользуемся уравнением (4.3) прямой, проходящей через точку M , и найдем неизвестное число k из условия принадлежности точки N искомой прямой. Подставляя в (4.3) вместо текущих координат x , y

Мы получили полезную формулу (4.6), выражающую угловой коэффициент прямой линии через координаты двух ее точек.

Замечание 4.3. Если данные точки M и N лежат на прямой параллельной

32