
3859
.pdf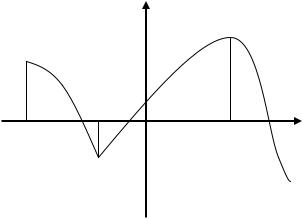
21
y
y =f(x)
a
0 |
c |
x |
1)[a;c] – промежуток убывания функции
2)а,с – критические точки
3)а,с – точки экстремума
4)xmin =а
66.Дана функция y= x2 x3 Найти y :
1)y = 2x+3 x 2
2)y = x+ x 2
3)y = x(2+3x)
4)y = 2 x3 3x4
67.Дана функция y= x2 e x Найти y :
1)y = 2x e x
2)y = 2x ex x2 ex
3)y = x e x (2 x)
4)y = 2x ex x2 ex
22
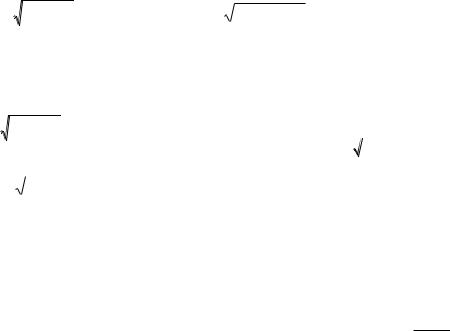
68. Точки, в которых функция не имеет производных:
y
3
2
y =f(x)
-3 |
-1 |
1 |
x |
-3
1)x = -1
2)x = 1
3)x = -3
4)x = 0
Дополните утверждения:
69.Если область определения функции D(f) симметрична относительно начала координат и для всех х из D(f) имеет место равенство f(-x)=f(x) ,то функция называется _______________.
70.Если область определения функции D(f) симметрична относительно начала координат и для всех х из D(f) имеет место равенство f(-x)=-f(x), то функция называется _______________ .
71.Если для любых х из интервала (а;b) большему значению аргумента
соответствует большее значение функции(x1<x2 →f(x1)<f(x2)), то функция f(x) называется ___________на этом интервале.
72.Если для любых х из интервала (а;b) большему значению аргумента
соответствует меньшее значение функции (x1<x2 → f(x1)>f(x2)),то функция называется ___________на этом интервале.
73.Пусть задано число a>0,a≠1. Тогда функция y=ax, называется
____________функцией.
74. Пусть задано число a>0,a≠1. Тогда функция y=logax называется
____________функцией.

23
75.Для любого действительного числа n функция y=x n называется
________функцией с показателем n.
76.Предел отношения приращения функции f(x0) к приращению аргумента x при x→0 , если этот предел существует, называется
___________функции в точке x 0 и обозначается f '(x 0).
Решение типовых задач на нахождение производной
Задача 1. Найти производную функции y=cos(x2)
Решение: При вычислении производных пользуются таблицей производных основных элементарных функций и теоремой дифференцирования сложной функции:
пусть y=f(u) дифференцируема в точке u0, u=f(x) дифференцируема в точке х0, причем (х0)=u0, тогда сложная функция y=f( (х)) дифференцируема в точке х0 и
|
|
|
|
|
|
|
|
|
|
y (x |
0 |
) f (u |
0 |
) (x |
0 |
) или y y |
|
u . |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
u |
x |
|
|
|
|
|
|
|
|
|
|
|
||||
В нашем случае u=x2, |
|
|
y=cos(u), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
sin( u ) 2x sin( x2 ) 2x |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
y cos( u ) |
u |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
1 |
|
|
|
cos( ax ) ax ln a ax ln a ctg( ax ) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
sin( a |
x |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
y ln( sin( ax ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
y 3 tg2( 3x ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
y e2x arctg( x3 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
e2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
arctg( x3 ) e2x |
|
arctg( x3 ) e2x arctg( x3 ) |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
3x |
2 |
|
|
||
|
|
e2x 2 arctg( x3 ) e2x |
|
|
|
|
|
|
|
3x2 e2x |
2 arctg( x3 ) |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3 2 |
|
|
|
6 |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 ( x |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 3 |
|
|
|
2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
3 tg2( 3x ) |
|
|
tg( 3x ) 3 |
|
|
|
2 tg( 3x ) 3 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
cos |
( 3x ) |
|
3 tg( 3x ) cos |
( 3x ) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin( x2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
sin( u ) 2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
y cos( u ) u |
|
|
2x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Задача 2. Найти производную функции |
|
y ln( sin( ax ) |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
Решение: |
|
y=ln(u), |
|
|
|
|
|
|
|
|
u=sin(v), |
v=ax, |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
v |
|
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
тогда |
y |
|
|
|
ln u |
|
|
|
|
sin v |
|
|
a x |
|
|
|
cos v a x |
ln a |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
cos( ax ) ax ln a ax ln a ctg( ax ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
sin( a |
x |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
24
Как видно из приведенных примеров, следует начинать дифференцирование с “внешней” элементарной функции, последовательно приближаясь к “внутренней”.
Задача 3. Найти производные функций:
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
а). y 3 tg2( 3x ) |
|
|
|
|
|
|
|
б). y ln 1 ex |
|
|||||||||
в). y e2x arctg( x3 ) |
|
|
|
|
|
|
|
|
||||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
||
а). |
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||||
3 tg2( 3x ) |
|
|
tg( 3x ) 3 |
|
tg( 3x ) 3 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
б). |
|
ln 1 ex e4x |
|
|
|
|
1 |
ln 1 |
ex e4x |
|
|
|||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
e4x
1 3 |
|
|
2 |
||
cos2( 3x ) |
3 |
|
cos2( 3x ) |
||
tg( 3x ) |
|||||
|
1 |
|
1 |
ex e4x |
4 |
ex 4e4x |
|
||||
2 |
1 ex e4x |
2(1 ex e4x ) |
|||||||||
|
|
|
|
|
e2x |
|
|
|
|
|
|
в). e2x arctg( x3 ) |
|
arctg( x3 ) e2x |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e2x 2 arctg( x3 ) e2x |
|
1 |
3x2 |
|||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
1 ( x3 )2 |
|
|
||
|
|
|
arctg( x3 ) |
|
|
|
|
|
e2x 2 arctg( x3 )
3x2
1 x6
Интеграл
Укажите номера правильных ответов.
78.На некотором промежутке функция может иметь:
1)Единственную первообразную;
2)Бесконечно много первообразных;
3)Несколько первообразных
.
79.Функция, для которой F(x)=4sinх-x является первообразной:
1)y=4sin(x)-1;
2)y=4cos(x)-1;
3)y=4sin(x)-x2/2;
4)y=4cos(x)-x2/2.
80.F(x)-первообразная для f(x).Функция, которая не будет первообразной для f(x):
1)y=F(x)+C;
2)y=3F(x);
3)y=F(x)+5;
4)y=3+F(x).
25
81.Первообразная для функции y=-sin(x)+1:
1)y=cos(x)+1;
2)y=xcos(x);
3)y=cos(x)+x;
4)y=-cos(x)+x.
82.Укажите верное соотношение:
1)dx x c;
2)sin xdx cos x c;
3)cos xdx sin x c;
4)xdx x 2 c.
83.Интеграл, не выражающийся через элементарные функции:
1)e x dx;
2)e x2 dx;
3)sin xdx;
4)x 2 dx.
84.Формула Ньютона-Лейбница:
b
1) f (x)dx F (a) F (b);
a
b
2) f (x)dx F (a) F (b);
a
b
3) f (x)dx F (a) F (b);
a
b
4) f (x)dx f (b) f (a).
a
85.Если F(x)-первообразная для f(x), то f (ax b)dx равен:
1)F(ax+b)+c;
2)a1 F (ax b) c;
3)a1 F (x) c;
4)b1 F (ax b) c.
86.Назовите верные утверждения:
1
1) dx 1;
0

26
1
2) e x dx e 1 e;
|
1 |
|
|
|
b |
|
|
|
|
||
3) |
|
|
0; |
|
f (x)dx |
||
|
a |
|
|
4)f (x)dx f (x).
87.Площадь фигуры, ограниченной линиями: y=x2; y=0; x=-1; x=1, равна:
1
1) x 2 dx;
0
1
2) x 2 dx;
1
1
3) x 2 dx;
1
1
4) 2 x 2 dx.
0
88. (1 x)2 dx равен:
1) x x 2 |
x3 |
c; |
|
||
3 |
|
|
2)x x3 c; 3
3)(1 x)3 c; 3
4) x |
x 2 |
|
x3 |
c. |
|
|
|||
2 |
3 |
|
||
89.Укажите верные соотношения
2
1) cos xdx 1;
0
1
2) dx 1;
0
1
3) e x dx e 1 e;
1
b
4) f (x)dx F (b) F (a).
a
90. Определите знаки указанных определенных интегралов:
1
1) ln xdx;
0,2

27
2
2) ln xdx;
1
0
3) cos xdx;
2
2
4) xdx.
1
91. Площадь фигуры, ограниченной линиями: y=x3; y=0; x=-1; x=1, равна:
1
1) x3 dx;
0
1
2) x3 dx;
1
01
3)x3 dx x3 dx;
1 0
1
4) 2 x3 dx.
0
92.Функции, являющиеся первообразными одной и той же функции:
1) 2x и 2x+4;
2) 2x и 2x-1;
3)sin(x) и sin(x)+2;
4) 2x и 2x+1. |
|
|
Дополните утверждения |
|
|
93. Дифференцируемая функция F(x) называется |
|
для f(x), |
определенной на том же промежутке, если F'(x) = f(x). |
|
|
94. Совокупность всех первообразных для функции f(x), определенных на некотором промежутке, называется интегралом.
95. Графики любых двух первообразных можно получить друг из друга параллельным переносом вдоль оси .
28
96. Если функция F(x) есть первообразная для функции f(x), то функция F(x)+ C также является для f(x) на том же промежутке.
97. Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической интегралов от этих функций в отдельности.
98. Постоянный множитель можно |
|
за знак интеграла. |
99. Если интегрируемая на [a;b] функция f(x) неотрицательна, то определенный интеграл численно равен криволинейной трапеции, ограниченной графиком функции f(x), осью Ox и прямыми x=a; x=b.
Решение типовых задач на нахождение неопределенных интегралов
Задача 1. Вычислить интеграл
2 33  x2 5
x2 5
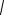 x dx
x dx
 x3
x3
Решение: Преобразуем подынтегральную функцию:
|
|
|
|
|
|
|
|
|
3 |
|
|
5 |
|
|
2 33 x2 5 x |
|
2 x |
|
1 |
||||||||||
|
|
|
|
|
||||||||||
|
2 3 x |
6 5 |
||||||||||||
|
|
|
|
|
|
|
|
|
x |
|||||
|
|
x |
3 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Далее представляем интеграл алгебраической суммы в виде суммы интегралов слагаемых, вынося постоянные множители за знаки интегралов, и, пользуясь таблицей интегралов, получим:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
2 33 x |
|
2 5 x |
|
|
|
|
|
|
|
|
dx 3 x |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
dx 2 |
|
2 |
6 dx 5 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
3 |
1 |
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
x |
2 |
|
|
|
|
|
|
3 |
x |
6 |
|
|
|
5ln |
|
|
c |
|
4 |
|
|
186 |
|
|
5ln |
|
c |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
x |
x |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
2 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Проверка: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
186 |
x |
5ln |
x |
c |
|
|
4x |
2 |
|
|
18x 6 |
5ln x c |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
1 |
|
|
|
|
|
|
|
1 |
|
1 |
1 |
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
1 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
18 |
|
|
|
x 6 |
|
|
5 |
|
|
|
|
x |
3 |
2 |
3x 3 5x |
2 |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 33 |
|
x 2 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Задача 2.

29
Вычислить интеграл |
|
sin xdx |
|
|
|
|
|
|
|
|
|
|
1 2cosx |
|
|
Решение:
Первый способ. Полагая
1 2cosx t , 2sin xdx dt , получим
|
|
sin xdx |
|
|
1 |
|
dt |
|
|
|
1 |
t |
1 |
|
|
|
1 |
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
2 dt |
2t 2 |
c |
t c |
1 2cosx c |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
1 2cosx |
|
|
2 |
|
|
t |
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||
Второй способ. |
|
|
|
|
sin xdx |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1 2cosx |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Умножая и деля на –2 и замечая, что 2sin xdx d(1 2cosx) , получим
|
|
|
sin xdx |
|
|
|
|
1 |
|
d 1 2cosx |
|
1 |
1 |
|
|
|
|
1 |
d 1 cosx |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cosx |
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 2cosx |
|
2 |
|
|
1 cosx |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
1 1 2cosx |
2 |
|
|
c 1 2cosx |
|
c |
1 2cosx c |
|||||||||||||||||||||||||||
|
|
|
2 |
|||||||||||||||||||||||||||||||||
|
2 |
|
1 |
1 |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2sin x |
|
|
|
sin x |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Проверка: |
|
|
1 2cosx c |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
1 cosx |
|
|
1 2cosx |
|||||||||||||||||||||||||||||||
Задача 3. Вычислить интеграл |
|
x 1 |
||||||||||||||||||||||||||||||||||
|
dx |
|||||||||||||||||||||||||||||||||||
x2 2x 3 |
||||||||||||||||||||||||||||||||||||
Для вычисления интеграла от функции, содержащей квадратный трехчлен, надо выделить полный квадрат их квадратного трехчлена, заменить переменную, в результате чего получим табличные интегралы.
Выделяя полный квадрат в знаменателе, имеем:
x 2x 3 x 1 2 2 . Далее, заменяя x 1 t , dx dt , получим:
|
|
x 1 dx |
|
|
|
|
|
x 1 dx |
|
|
|
tdt |
|
|
|
1 |
|
|
d t 2 2 |
|
1 |
ln t2 2 c |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x 2 2x |
3 |
x 1 2 |
2 |
|
t2 2 |
2 |
|
|
t2 2 |
2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
1 |
ln x 2 2x 3 c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1 |
ln x2 |
2x 3 c |
|
|
1 |
|
|
|
2x 2 |
|
|
|
|
|
x 1 |
|
|
|||||||
Проверка: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x |
2x 3 |
|
|
x |
2x |
3 |
|||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Задача 4. Вычислить интеграл 
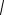 x ln xdx .
x ln xdx .
Решение: При вычислении этого интеграла надо применить метод
интегрирования по частям. Положив ln x u , dv |
x dx , найдем: |
||||||||||||
|
|
|
|
1 |
|
3 |
|
|
|||||
du |
1 |
|
v |
|
dx x |
|
dx |
2 |
x |
|
. Подставляя в формулу |
||
dx ; |
x |
2 |
2 |
||||||||||
|
|
||||||||||||
|
x |
|
|
|
|
|
3 |
|
|
|
|
||
udv u v vdu , получим
30
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
x ln xdx |
|
x 3 ln x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
3 |
3 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
x |
|
ln x |
|
|
x 2 dx |
|
|
|
x |
|
|
ln x |
|
|
|
|
|
|
x |
|
c |
|
|
x |
|
ln x |
|
|
|
|
c |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
ln x |
c |
|
|
|
|
|
x3 |
ln x |
|
x |
3 ln x |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Проверка: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ln x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
x ln x |
|
|
|
x |
|
|
|
|
|
x |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
2 |
|
3 |
|
|
|
x |
3 |
|
3 |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
2 |
|
|
|
|
|
|
|
|||
|
|
||||
|
|||||
|
3 |
|
|
|
|
|
|
|
|
|

 x ln x
x ln x
При интегрировании по частям важен выбор функции u и v. В качестве u выбирается та часть подынтегрального выражения, которая существенно упрощается при дифференцировании. За dv – та часть подынтегрального выражения вместе с dx, которая может быть проинтегрирована.
Решение типовой задачи на нахождение площади фигуры с помощью определенных интегралов
Задача 1. Найти площадь фигуры, ограниченной прямой у = х и параболой у = 2 – х2 .
Решение: Найдем абсциссы точек пересечения прямой с параболой:
|
|
|
|
|
|
|
Y |
|
y x |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
||
|
|
2 |
|
|
|
|
|
|
y 2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
|
|
1 |
х – 2 + х2 |
= 0 |
|||
|
|
|
|
|
|
|
|
х1 |
= –2; х2 |
= 1 |
||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Воспользуемся формулой для вычисления площади фигуры,
b
ограниченной двумя кривыми: S f2 x f1 x dx
a
При а = –2, b = 1, f2(x) = 2 – x2, f1(x) = x
Получим:
|
|
|
|
x |
|
|
x |
|
1 |
|
|
|
1 |
2 x 2 x dx |
|
|
3 |
|
|
2 |
|
|
|
S |
|
2x |
|
|
|
|
|
|
|
||
|
|
|
3 |
|
2 |
|
2 |
|
|||
|
2 |
|
|
|
|
|
|||||
|
|
1 |
|
1 |
|
|
|
8 |
|
|
|
9 |
|
|||
2 |
|
|
|
|
|
|
|
4 |
|
|
|
2 |
|
|
|
4,5 |
|
|
|
|
|
|
|||||||||||
|
|
3 |
|
2 |
|
|
|
3 |
|
|
|
2 |
|
|||
