
2373
.pdfФедеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования «Воронежская государственная лесотехническая академия»
МАТЕМАТИКА
ЭЛЕМЕНТЫ ТЕОРИИ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Методические указания для самостоятельной работы студентов специальности
190601 – Автомобили и автомобильное хозяйство
Воронеж 2010
2
УДК 517.53
Котко, Л. А. Математика. Элементы теории функций комплексного переменного [Текст] : методические указания для самостоятельной работы студентов специальности 190601 – Автомобили и автомобильное хозяйство / Л. А. Котко, С. В. Писарева ; Фед. агентство по образованию, ГОУ ВПО
«ВГЛТА». – Воронеж, 2010. – 28 с.
Печатается по решению учебно-методического совета ГОУ ВПО «ВГЛТА» (протокол № 8 от 11 июня 2009 г.)
Рецензент канд. физ.-мат. наук, доц. кафедры высшей математики и физико-математического моделирования ВГТУ А.П. Дубровская

3
1.КОМПЛЕКСНЫЕ ЧИСЛА
1.1.Комплексные числа. Исходные определения
Как известно, квадратное уравнение с действительными коэффициентами не всегда имеет действительные корни. Это обстоятельство приводит, естественно, к расширению понятия о числе, к введению чисел, частным случаем которых являются действительные числа.
Определение. Комплексным числом z называется выражение z = a + ib,
где a и b – действительные числа, i – мнимая единица, определяемая равенством
i =  −1 или i2 = −1.
−1 или i2 = −1.
Число a называется действительной или вещественной частью z и обозначается Re z, число b - мнимой частью и обозначается Im z.
Если a=0, то число 0 + ib = ib называется чисто мнимым, если b = 0, то получается действительное число a + i0 = а. Комплексные числа z = a + ib и
z =a – ib, отличающиеся только знаком мнимой части, называются сопряженными.
Два комплексных числа z1 = a1 + ib1 и z2 = a2 + ib2 считаются равными z1 = z2, если a1 = a2, b1 = b2, то есть равны их действительные и мнимые части. В частности, z = 0, если a = 0 и b = 0.
Если для геометрического изображения действительных чисел используются точки числовой прямой, то для изображения комплексных чисел служат точки координатной плоскости 0xy.
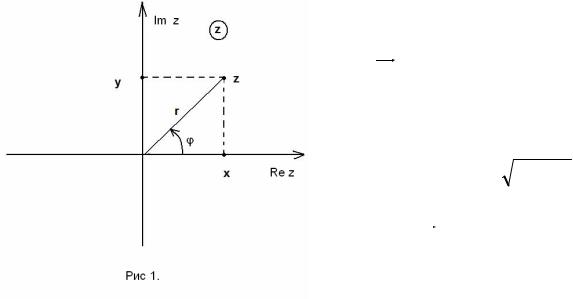
Любое комплексное число z = x + iy можно изобразить на плоскости 0xy в виде точки z(x,y) с координатами x и y (см. рис. 1). Обратно, каждой точке
плоскости |
соответствует комплексное число. Плоскость, |
на которой |
|
изображают |
комплексные числа, |
называется плоскостью |
комплексного |
переменного z ( на плоскости ставят символ z в кружке). |
|
||
Ось Ox, на которой расположены действительные числа, и ось 0y, на которой расположены чисто мнимые числа, называются соответственно действительной и мнимой осями.
4
С каждой точкой z(x,y) комплексной плоскости связан радиус-вектор этой
точки 0z, длина которого r называется модулем комплексного числа z и
обозначается |
| z | |
|
|
|
|
r =| z |= x2 + y2 . |
|
||
Угол φ , образованный радиусом- |
||||
вектором 0z с осью |
0x, |
называется |
||
аргументом |
комплексного |
числа z |
и |
|
обозначается |
Arg z. |
Аргумент |
φ |
|
определяется не однозначно, а с точностью до слагаемого 2πk, где k – любое целое число. Из значений φ=Arg z выделяется главное значение arg z, удовлетворяющее условию −π < arg z ≤π.
Очевидно, что выполняется
x = r cosϕ, y = r sin ϕ.
Следовательно, комплексное число z = x + iy можно представить в виде z = r(cos ϕ + i sin ϕ)
который называется тригонометрической формой комплексного числа.
1.2. Основные действия над комплексными числами
Арифметические операции над комплексными числами определяются естественным образом из правил сложения и умножения многочленов x1 +iy1 и x2 +iy2 , если считать i2 = –1.
Если z1 = x1 +iy1 , z2 = x2 +iy2 , то определим сумму |
(разность) |
комплексных чисел |
|
z1 ± z2 = x1 ± x2 +i( y1 ± y2 ); |
|
произведение комплексных чисел |
|
z1 z2 = (x1x2 − y1 y2 ) +i(x1 y2 + x2 y1 ); |
|
частное от деления двух комплексных чисел

5
z1 |
= |
z1 |
z2 |
|
|
= |
(x1 x2 + y1 y2 ) +i(x2 y1 − x1 y2 ) |
(z2 ≠ 0). |
z2 |
|
|
|
|
x2 2 + y2 2 |
|||
|
|
|
||||||
|
z2 z2 |
|
||||||
В результате операций сложения, вычитания, умножения и деления комплексных чисел получается снова комплексное число. Если правила действий над комплексными числами применить к действительным числам, рассматривая их как частный случай комплексных, то эти правила будут совпадать с обычными правилами действий, известными из арифметики.
Пусть комплексные числа z1 и z2 даны в тригонометрической форме
z1 = r1 (cosϕ1 +isinϕ1 ), |
z2 |
= r2 (cosϕ2 +isinϕ2 ). |
Перемножим эти числа, используя |
тригонометрические формулы |
|
cos(ϕ1 +ϕ2 ) = cosϕ1 cosϕ2 −sin ϕ1 sin ϕ2 |
и |
sin(ϕ1 +ϕ2 ) = sin ϕ1 cosϕ2 + |
+cosϕ1 sinϕ2 . Получим |
|
|
z1 z2 = r1 r2[cos(ϕ1 +ϕ2 ) +i sin(ϕ1 +ϕ2 )],
откуда видно, что модуль произведения двух комплексных чисел равен произведению модулей сомножителей, а аргумент произведения равен сумме аргументов сомножителей.
Аналогично, поделим теперь z1 на z2 , в результате получим
z1 |
= |
r1 |
[cos(ϕ −ϕ |
2 |
) + i sin(ϕ −ϕ |
2 |
)]. |
|
|
||||||
z2 |
|
r2 |
1 |
1 |
|
||
|
|
|
|
|
|
(Для проверки этого равенства достаточно умножить делитель на частное.) Таким образом, модуль частного двух комплексных чисел равен частному модулей делимого и делителя, а аргумент частного равен разности аргументов делимого и делителя.
Пример 1.1. Комплексные числа z1 =1−  3 i и z2 = - 1 + i представьте в
3 i и z2 = - 1 + i представьте в
тригонометрической форме и найдите z1 · z2 |
|
z1 |
. |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||
и z2 |
|
|
|
|
|
|
|||||||||
|
|
Решение. |
Найдем |
модуль |
комплексного |
|
|
числа |
z1: |
||||||
r1 = |
|
z1 |
|
= (1)2 +(− |
3)2 = 2. |
Из соотношений |
cosϕ1 = |
1 |
, |
sinϕ1 = − |
3 |
|
|||
|
|
||||||||||||||
|
|
2 |
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
определим аргумент числа z1 |
|
(берем его главное значение): |
ϕ1 = arg z1 = − |
π |
, |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
т.о. |
z1 = 2(cos(−π ) +isin(−π )). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Аналогично, |
r2 = |
|
z2 |
|
|
= |
|
|
|
(1)2 +12 |
= 2, |
cosϕ2 = − |
|
1 |
|
, |
sinϕ2 |
= |
|
1 |
. |
Из |
|||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
2 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
этого следует, что ϕ2 = arg z2 |
= |
|
и z2 |
= |
|
|
2(cos |
3π |
+isin |
3π |
). |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
4 |
|
|
|
4 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Найдем теперь z1 z2 |
и |
|
|
|
z1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
z |
z |
2 |
= 2 2(cos |
5 |
π +isin |
5 |
π), |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
12 |
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
z1 |
= |
2 |
(cos(− |
13 |
|
π) +i sin(− |
|
13 |
π)) = |
2 |
(cos |
11 |
π +i sin |
11 |
π). |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
2 |
12 |
|
12 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
12 |
|
|
|
12 |
|
|
|
|
|
|
|||||||||||||||||
1.3.Возведение комплексного числа в степень и извлечение корня из комплексного числа
Так как при умножении комплексных чисел их модули перемножаются, а аргументы складываются, легко получить формулу возведения комплексного числа в натуральную степень n, известную как формула Муавра
[r(cosϕ +isinϕ)]n = r n (cos nϕ +isin nϕ).
|
Пример 1.2. Найти |
(1− |
|
3 i)9 . |
|
|
|
|
|
|
|
|||||||||||
|
Решение. |
|
|
В |
|
предыдущем |
|
примере |
мы |
показали, |
что |
|||||||||||
1− |
3 i = |
|
|
− |
π |
|
|
|
π |
|
По формуле Муавра получаем |
|
|
|||||||||
2 cos |
3 |
|
+isin − |
|
|
. |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||
(1− |
3 i) |
9 |
= |
|
|
− |
π |
|
|
|
|
π |
|
9 |
9 |
[cos(−3π) +isin(−3π)] = 2 |
9 |
(−1 |
+0i) = −512. |
|||
|
2cos |
3 |
|
+isin − |
3 |
|
= 2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Обратимся к извлечению корня из комплексного числа.
Корнем n-ой степени из комплексного числа называется такое комплексное число, n-ая степень которого равняется подкоренному числу, то есть
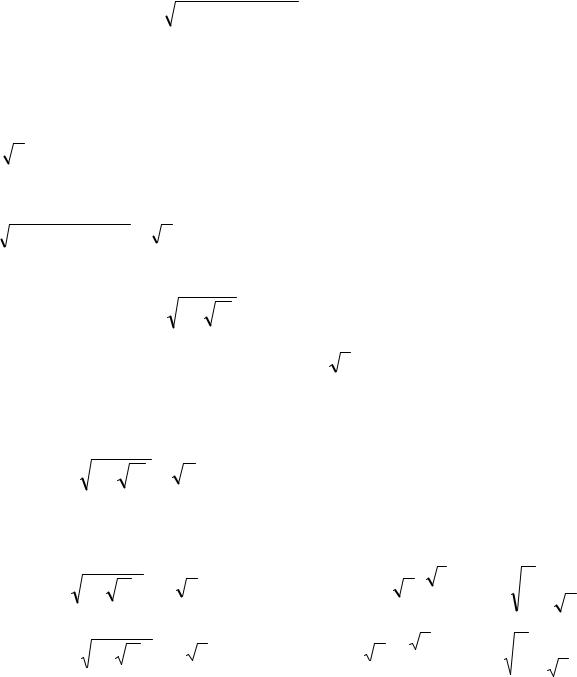
7
n r(cosϕ +isinϕ) = ρ(cosψ +isinψ).
Возведем обе части равенства в n –ую степень
ρn (cos nψ +i sin nψ) = r(cosϕ +i sinϕ).
Отсюда следует, что ρn |
= r |
и ψ =ϕ +2πk, |
где k Z, |
и, соответственно, |
|
||||
ρ = n r и |
ψ = ϕ + 2πk , |
k Z . Таким образом, |
корень n-ой степени из |
||||||
|
n |
|
|
|
|
|
|
|
|
комплексного числа z (z ≠ 0) имеет n различных значений |
|
|
|
|
|||||
n r(cosϕ +isinϕ) = n |
r (cos ϕ +2πk + +isin |
ϕ +2πk ), |
где k = 0, 1, 2,…, n-1. |
|
|||||
|
|
|
n |
n |
|
|
|
|
|
При k = n, n + 1,… значения корня будут повторяться. |
|
|
|
|
|
||||
Пример 1.3. Найти |
1− |
3 i . |
|
|
|
|
|
|
|
Решение. Ранее было показано, что 1− |
|
|
π |
|
π |
Из |
|||
3 i = 2 cos − |
|
+isin − |
. |
||||||
|
|
|
|
|
|
3 |
|
3 |
|
последней формулы следует, что
1− 3 i = 2 cos
|
π |
|
|
|
π |
|
|
− |
3 |
+2πk |
|
− |
3 |
+2πk |
|
|
|
|
|
|
|
|
|
|
|
2 |
+i sin |
|
2 |
||
|
|
|
, k = 0, 1, |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
откуда получаем два значения корня
|
|
|
|
|
|
|
π |
|
|
π |
|
|
|
3 |
|
1 |
|
|
3 |
|
i |
|
z = ( 1− |
3 i ) |
1 |
= |
2 cos |
− |
|
+i sin |
− |
|
= |
2 |
|
|
− |
|
i |
= |
|
− |
|
, |
|
|
|
|
|
|||||||||||||||||||
1 |
|
|
|
|
|
6 |
6 |
|
|
|
2 2 |
|
|
2 |
|
2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
5 |
|
5π |
|
|
|
− 3 |
|
1 |
|
|
3 |
|
i |
|
z |
2 |
= ( 1 |
− |
3 i ) |
2 |
= |
2 cos |
|
π +i sin |
|
= |
2 |
|
|
+ |
|
i |
= − |
|
+ |
|
. |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
6 |
|
6 |
|
|
|
2 |
|
2 |
|
|
2 |
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
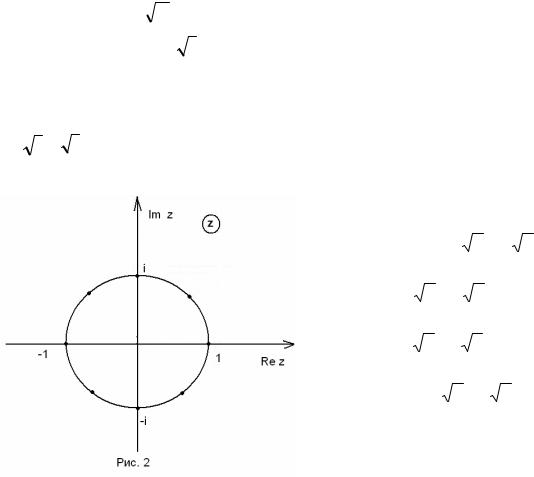
Замечание. Корень n-й степени из действительного числа A, отличного от нуля, также имеет n значений, так как действительное число является частным случаем комплексного и может быть представлено в тригонометрической форме:
A = |
|
|
A |
|
(cos 0 +isin 0) |
при |
A > 0; |
|||
|
|
|
||||||||
A = |
|
A |
|
(cosπ +isinπ) |
при |
A <0. |
||||
|
|
|||||||||
8
На комплексной плоскости значения корня n-ой степени из числа z представляют равностоящие друг от друга точки z1, z2,…, zn, расположенные на
окружности радиуса n r. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 1.3. Найти 8 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. Представим 1 в тригонометрической форме |
|
1 =1(cos0 +isin 0) . По |
|||||||||||||||||||||||||
формуле вычисления корней из комплексных чисел вычисляем |
|
|
|
|
|
|
|
|
|||||||||||||||||||
8 1 = 8 1(cos |
0 + 2πk |
+i sin |
0 + 2πk |
) , где k = 0, 1, 2,…, 8. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Получаем |
|
|
восемь |
|
|
|
|
различных |
|||||||||||||||
|
|
|
|
значений корня (см. рис. 2) |
|
|
|
|
|||||||||||||||||||
|
|
|
|
z =1, |
|
z |
|
|
= |
|
|
|
2 |
|
|
|
+i |
2 |
, z |
3 |
= i, |
||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
z4 |
= − |
|
|
2 |
|
|
+i |
|
2 |
|
|
, z5 = −1, |
|
||||||||||
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
z6 |
= − |
|
|
|
2 |
|
|
−i |
|
2 |
, z7 = −i, |
|
|||||||||||
|
|
|
|
|
2 |
|
|
|
2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
z8 |
|
= |
|
|
2 |
−i |
|
2 |
. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
2. ЭЛЕМЕНТЫ ТЕОРИИ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
2.1. Понятие функции комплексного переменного
Пусть даны две плоскости комплексных чисел z = x + iy и w = u +iv и пусть комплексное переменное z принимает всевозможные значения из некоторого множества D в плоскости z.
Определение. Если каждому значению z из D по некоторому закону поставлено в соответствие определенное комплексное число w из множества G в плоскости w, то говорят, что на множестве D задана однозначная функция комплексного переменного w = f(z).

9
Если существуют значения z D, каждому из которых соответствует несколько разных значений w, то функция w = f(z) называется многозначной.
Пример 2.1. Функция w = z2 является однозначной, так как каждому значению переменного z из комплексной плоскости z соответствует единственное комплексное число, равное квадрату этого значения. Найдем действительную и мнимую части w. Имеем
w = u + iv = z2 = (x + iy)2 = x2 + i2xy
следовательно, действительная часть u = x2 – y2, Вообще, если w = u + iv есть функция от
являются функциями x и y, то есть
+i2 y2 = (x2 − y2 ) + i2xy,
амнимая часть v = 2xy.
z = x + iy, то переменные u и v
u = u(x, y), v = v(x, y).
Определение. Область D, ограниченная замкнутой самонепересекающейся линией Г, называется односвязной.
Пример 2.2. Примером односвязной области в комплексной плоскости может служить круг с центром в некоторой точке z0 радиуса r, задаваемый
неравенством |
|
z − z0 |
|
< r . |
|
|
|||
Определение. |
|
Если область D ограничена двумя замкнутыми, не |
||
пересекающимися и не самопересекающимися линиями Г1 и Г2, то она называется двусвязной. Область является двусвязной и в том случае, если внутренняя линия вырождается в точку или в дугу непрерывной линии.
Пример 2.3. Двусвязной областью является, например, кольцо с центром в точке z0, задаваемое неравенствами r < z − z0 < R .
Определение. Говорят, что однозначная функция w = f(z) при z → z0 имеет определенный предел А (A = a + ib), если для любого числа ε>0 найдется такое число δ>0, что из неравенства z − z0 <δ следует неравенство
f (z) − A <ε. В этом случае пишут
lim f (z) = A.
z→z0
Определение. Функция w = f(z) называется непрерывной в точке z0, если
lim f (z) = f (z0 ). Функция, непрерывная в каждой точке некоторой области D,
z→z0
называется непрерывной в этой области.
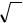
10
Непрерывность f(z) в точке z0 эквивалентна непрерывности функций u(x,y) и v(x,y) в точке (x0,y0).
Введем в рассмотрение функции комплексного переменного ez, sin z, cos z, sh z, ch z. Показательная функция w = ez определяется так
ez = ex+iy = ex (cos y +i sin y),
то есть w(z) =ex (cos y +isin y).
Синус и косинус комплексного переменного, а также гиперболические синус и косинус определяются по формулам
sin z = |
eiz −e−iz |
; |
cos z = |
eiz + e−iz |
|
|
2i |
2 |
|
||||
|
|
|
|
|||
sh z = |
ez −e−z |
; |
ch z = |
ez +e−z |
. |
|
2 |
2 |
|||||
|
|
|
|
Легко видеть, что sin z и sh z связаны соотношением sh z= –i sin iz, а cos z и ch z соотношением ch z = cos i z. Справедлива формула Эйлера
eiz = cos z + i sin z,
из которой следует показательная форма комплексного числа z = reiϕ .
Известные из элементарной математики формулы
z |
z |
|
z |
+z |
|
|
ez1 |
z −z |
|
e 1 |
e |
2 |
= e 1 |
|
2 |
; |
|
= e 1 |
2 ; |
|
ez2 |
sin(z1 ± z2 ) = sin z1 cos z2 ±cos z1 sin z2 ; cos(z1 ± z2 ) = cos z1 cos z2 sin z1 sin z2
справедливы и для комплексных значений аргументов z1 и z2.
Приведем некоторые многозначные функции комплексного переменного:
а) корень целой степени n w = n z;
б) логарифмическая функция Lnz=ln |z| + i(arg z + 2πk);
в) степенная функция zα = eαLnz (α – действительное число). Эти функции многозначны во всех точках, кроме точек z=0 и z=∞, в которых они однозначны – такие точки называют точками ветвления. Если на плоскости z провести разрез, соединяющий точки ветвления (например, вдоль положительной действительной полуоси), то можно говорить об однозначных ветвях многозначных функций.
