540

2

ББК 2

З-15

Задохина, Н. В.

Дискретная математика в примерах и задачах : учебное по-

собие / Н. В. Задохина ; Н. М. Дубинина ; Б. В. Борисов. – М. : Московский университет МВД России, 2012. – 74 с.

Настоящее пособие знакомит читателей с важными разделами дискретной математики и состоит из четырех глав: множества, элементы математической логики, комбинаторика и элементы теории графов, которые разбиты на параграфы. В начале каждого параграфа приводится необходимый минимум теоретических знаний, затем подробно разбираются модельные примеры. Текст отличается доступностью и ясностью написания, снабжен большим количеством иллюстраций.

В конце каждой главы приводятся задания для самостоятельного решения, направленные на осознанное закрепление основных понятий и алгоритмов. Ответы к заданиям помещены в конце пособия.

Издание предназначено для курсантов, студентов и слушателей, проходящих обучение в рамках дисциплин: «Дискретная математика», «Математика», «Математика и информатика», а также для тех, кого интересуют классические и современные методы дискретного анализа.

ББК 2

Рецензенты: начальник кафедры информационной безопасности Московского университета МВД России, кандидат технических наук К. К Борзунов; старший преподаватель кафедры информационных технологий управления органами внутренних дел Академии управления МВД России, кандидат технических наук М. П. Дубинин.

©Московский университет МВД России, 2012

©Задохина Н. В., 2012

©Дубинина Н. М., 2012

©Борисов Б. В., 2012

4

ВВЕДЕНИЕ

Дискретная математика (или дискретный анализ) – самостоя-

тельный раздел математики, изучающий свойства различныхдискретных (прерывных) структур, которые возникают как в самой математике, так и в ее приложениях.

Несмотря на то, что отдельные направления дискретной математики зародились еще в глубокой древности и совершенствовались параллельно с классической математикой, наиболее интенсивно дискретная математика стала развиваться в последнее столетие.

Специфика задач дискретной математики в первую очередь предполагает отказ от основных понятий классической математики– предела и непрерывности. Поэтому для задач дискретной математики обычные средства классического анализа являются вспомогательными. Дискретная и непрерывная математика взаимно дополняют друг друга. Понятия и методы одной часто используются в другой. Один и тот же объект может рассматриваться с двух точек зрения, и в зависимости от этого выбирается непрерывная или дискретная математика.

Внастоящее время дискретная математика занимает важное место

вобщем курсе математической подготовки студентов высших учебных заведений. Интерес к ней обусловлен широким кругом ее применения в таких областях знаний, как электроника, информатика, оптимизация производственных процессов, теория принятия решений и т.д.

Объектом изучения дискретной математики являются элементы различных множеств и действия над ними; предметом – методы формализованного представления систем, используемые при моделировании, исследовании и анализе социально-экономических и правовых процессов и явлений. К ним относятся: методы, основанные на теорети- ко-множественных представлениях, графы, математическая логика и др.

Результатом изучения данной дисциплины должно стать умение описывать дискретные математические объекты, строить математические и прикладные дискретные модели и работать с ними, что составляет необходимую часть успеха профессиональной деятельности современного специалиста.

Предлагаемое учебное пособие содержит достаточно примеров, иллюстраций, схем и таблиц, позволяющих неформально усвоить материал важнейших разделов дискретной математики: множества, элементы математической логики, комбинаторика и элементы теории графов.

5

Глава 1. МНОЖЕСТВА

§ 1. Понятие множества

Создателем теории множеств является немецкий ученый Георг Кантор (1845–1918). Он определил, что «множество есть многое, мыслимое нами как единое».

В обычной жизни мы часто употребляем слово«множество»: множество людей, книг, законов и т.д. Тем самым каждый раз мы группируем (порой неосознанно) объекты по признакам, свойствам, характеристикам.

Множество – группа или набор объектов (предметов), обладающих каким-либо общим для всех них свойством или признаком.

Высказанное утверждение является не определением, а лишь разъяснением. Такого определения попросту не существует, поскольку понятие множества является первичным(как точка, число и др.), на основании которого строятся остальные понятия математики.

Можно говорить не только о множествах, элементами которых являются материальные объекты, но и о множествах, элементы которых – некоторые абстрактные понятия (числа, геометрические фигуры, символы и т.п.).

Множества обозначаются прописными буквами латинского алфавита (A, B, C, …), а их элементы – строчными (a, b, c, …).

Принадлежность элементов (точек) к множеству обозначается знаком «Î». Так, запись a Î A означает, что элемент a принадлежит множеству A. Если же a не принадлежит множеству A, то пишут a Ï A.

Пример 1. Пусть A – множество делителей числа 12. Тогда 2 Î А, а 5 Ï А.

Если число элементов множества конечно, то множество называется конечным, в противном случае – бесконечным.

Пример 2. Множество персонажей басен Крылова– конечное множество, а все натуральные числа – бесконечное множество.

6

Сразу оговорим, что понятие «множество» не следует понимать буквально и толковать его как совокупность, содержащую «много» элементов.

Встречаются множества, не содержащие ни одного элемента. Такие множества называют пустыми и обозначают символом Æ .

Пример 3. Множество людей, чей рост составляет 3 м, – Æ (пустое множество).

Существуют разные способы задания множеств. Конечное множество можно задавать перечислением всех его элементов, например, A = {a1; a2; a3;...; an}, где a1, a2, a3, …, an – объекты любой природы.

Пример 4. Пусть B – множество планет солнечной системы. Тогда

B = {Венера, Земля, Марс, Меркурий, Нептун, Плутон, Сатурн, Уран, Юпитер}.

Задать множество можно также с помощью правила, позволяющего определить, является ли данный объект элементом множества или нет.

Пример 5. Пусть С – множество решений уравнения x2 – 3x + 2 = 0. Тогда множество С = {x | x2 – 3x + 2 = 0}. В такой записи правило, задающее множество, отделено вертикальной чертой(вертикальная черта | дословно обозначает: таких, что). Очевидно, что элементами множества С являются числа 1 и 2, т.е. С = {1; 2}.

Запись «A Ì B» означает, что каждый элемент множества A принадлежит множеству B. В этом случае множество A называют подмножеством множества B. Каждое непустое множество A имеет, как минимум, два подмножества: пустое множество Æ и само множество A.

Пример 6. Пусть A – множество всех квадратов, а B – множество всех четырехугольников. Очевидно, что A Ì B.

Если для двух множествА и В одновременно справедливы утверждения A Ì B и В Ì А, то множества А и В состоят из одних и тех же элементов. Такие множества называются равными и пишут А = В.

7

Пример 7. Пусть А – множество решений уравнения x + 2 = 7; В – множество решений уравнения x + 4 = 9. Тогда множество А = = {x | x + 2 = 7}, а множество В = {x | x + 4= 9}. Очевидно, что А = {5}, В = {5}, т.е. А = В.

Множества, элементами которых являются числа, называются чи-

словыми множествами.

Напомним, что множество всех действительных чисел разбивается на два подмножества – рациональных и иррациональных чисел.

Рациональным называется число, которое можно представить в

виде p , где р и q – целые числа, причем q ≠ 0. Иррациональным на- q

зывается всякое вещественное число, которое не является рациональ-

ным. Всякое рациональное число p является либо целым, либо его q

можно представить в виде конечной или периодической бесконечной десятичной дроби. Иррациональное же число представляется непериодической бесконечной десятичной дробью. Например, рациональ-

3 1

ные числа 4 и 3 представляются соответственно следующими деся-

тичными дробями: 0,75 и 0,333...; иррациональные числа 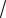2 и π представляются соответственно непериодическими бесконечными десятичными дробями: 1,41421356... и 3,14159... .

Применяются следующие обозначения числовых множеств:

-R – множество действительных чисел;

-I – множество иррациональных чисел (I Ì R);

-Q – множество рациональных чисел (Q Ì R);

-N – множество натуральных чисел. Множество N содержит числа, используемые для счета (целые положительные числа), и является подмножеством множества Q (N Ì Q);

-Z – множество целых чисел. Множество Z содержит целые отрицательные числа, 0, целые положительные числа и является подмножеством множества Q (Z Ì Q).

Множество действительных чисел R называется числовой прямой и обозначается (–∞; +∞).

Пример 8. Даны следующие числовые множества: R – действительных чисел; Q – рациональных чисел; N – натуральных чисел; Z –

8

целых чисел. Требуется расположить буквы, обозначающие эти множества, так, чтобы каждая предыдущая буква являлась подмножеством следующей. Очевидно, что справедливым будет следующее утверждение: N Ì Z Ì Q ÌR.

Пусть а и b – два действительных числа, причем а < b. Множество действительных чисел x, удовлетворяющих определенным неравенствам, называется числовым промежутком. Будем использовать следующие обозначения:

-отрезок: [a, b] = {x | a ≤ x ≤ b};

-интервал: (a, b) = {x | a < x < b};

-полуинтервалы: (a, b] = {x | a < x ≤ b}; [a, b) = {x | a ≤ x < b}.

Интервал (а, b) отличается от отрезка [а, b] лишь тем, что ему не

принадлежат границы а и b. Это отличие играет существенную роль во многих математических вопросах. Кроме того, интервал (а, b) не содержит ни наибольшего, ни наименьшего числа, в то время как в отрезке [а, b] такими числами являются соответственно а и b.

Интервалы и полуинтервалы могут быть как конечными, так и бесконечными; отрезки – только конечными.

Пример 9. Пусть множество А=(–5; 11], а множество В=[–23; 17). Изобразим данные множества, заданные числовыми промежутками, на числовой прямой и выясним, является ли множество А подмножеством множества В.

Напоминаем, что при изображении числовых промежутков закрашенными кружками обозначаются крайние точки, принадлежащие промежутку, а светлыми кружками– не принадлежащие промежутку (так называемые «выколотые» точки).

Рис. 1.1

Из рисунка видно, что все элементы множества А входят в множество В. Очевидно, что А Ì В (рис. 1.1).

9

§ 2. Операции над множествами

Из множеств с помощью определенных операций можно образовывать новые множества. Для наглядного представления операций над множествами и различных соотношений между множествами удобно использовать диаграммы Эйлера-Венна, на которых множества изображаются в виде фигур, ограничивающих совокупность точек на плоскости. Знаменитый швейцарский математик Леонард Эйлер первый использовал идею изображать множества с помощью кругов, а позднее аналогичный прием применил известный английский логик Джон Венн. Отсюда и название: диаграммы Эйлера-Венна.

Ниже подробно рассмотрим каждую операцию.

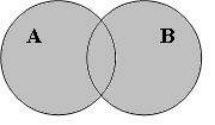
Объединением (или логической суммой) множеств А и В называется множество, которое состоит из всех элементов, принадлежащих хотя бы одному из этих множеств. Объединение множеств А и В обозначается À È Â (рис 1.2).

Рис. 1.2

Пример 10. Пусть множество А = {Татьяна, Ольга, Алина, Петр, Ирина, Виталий}, а множество В = {Иван, Ольга, Мария, Николай, Петр, Ирина}. Тогда À È Â ={Татьяна, Ольга, Алина, Петр, Ирина, Виталий, Иван, Мария, Николай}. Очевидно, что множество À È Â со-

стоит из всех элементов, которые хоть раз присутствуют в какомлибо из множеств А или В.

Пример 11. Пусть множество А = {1; 2; 3; 4; 5; 6}, а множество

В = {3; 6; 9; 12}. Тогда À È Â = {1; 2; 3; 4; 5; 6; 9; 12}.

Пример 12. Пусть множество А = [–11; 3], а множество В = (0; 10]. Тогда À È Â = [–11; 10] (рис. 1.3).

10

Рис. 1.3

Пример 13. Пусть множество А = (–5; 11], а множество В = [–23; 17). Тогда À È Â = [–23; 17) (рис. 1.4).

Рис. 1.4

Очевидно, что в данном примере À È Â будет само множествоВ, так как А Ì В.

Пересечением (или логическим произведением) множеств А и В называется множество, которое состоит из всех элементов, принадлежащих одновременно каждому из этих множеств. Пересечение множеств А и В обозначается À Ç Â (рис. 1.5).

Рис. 1.5

Пример 14. Пусть множество А = {Татьяна, Ольга, Алина, Петр, Ирина, Виталий}, а множество В = {Иван, Ольга, Мария, Николай, Петр, Ирина}. Тогда À Ç Â = {Ольга, Петр, Ирина}. Очевидно, что множество À Ç Â состоит из всех элементов, которые принадлежат множеству А и множеству В одновременно.