
343
.pdf
Рис. 1.3. Кумулята распределения по уровню преступности
Таблица 1.4
Количество несовершеннолетних, стоящих на профилактическом учете в территориальном органе внутренних дел
Название района |
Количество несовершеннолетних |
|
|
Качинский |
71 |
|
|
Рыбинский |
86 |
|
|
Уславский |
96 |
|
|
Николаевский |
101 |
|
|
Вощажниковский |
431 |
|
|
На примере данных таблицы 1.4 видно принципиальное различие между медианой и средней арифметической величиной. Медиана не зависит от значений признака на краях ранжированного ряда. Если бы даже количество несовершеннолетних в районе с наибольшим их числом стало бы вдруг вдвое больше имеющегося, величина медианы нисколько не изменилась бы. Поэтому часто медиану используют как более надежный показатель типичного значения признака, нежели средняя арифметическая, если ряд значений неоднороден, включает резкие отклонения от средней.
11
В данном ряду средняя величина количества несовершеннолетних, равная 157, сложилась под значительным влиянием наибольшего значения. Для 80 % рассмотренных в примере территориальных органов внутренних дел количество несовершеннолетних, стоящих на профилактическом учете в данном органе, меньше среднего, и лишь 20 % – больше. Вряд ли такую среднюю можно считать типичной величиной.
При четном числе единиц совокупности за медиану принимают арифметическую среднюю величину из двух центральных значений признака, например, при десяти значениях признака – среднюю из пятого и шестого значений в ранжированном ряду.
В интервальном вариационном ряду для нахождения медианы применяется формула:
 ,
,
где: Ме – медиана; хМе – начальное значение интервала, содержащего медиану;
iMe – величина медианного интервала; f – сумма частот ряда;
SMe – 1 – сумма накопленных частот, предшествующих медианному интервалу;
fMe – частота медианного интервала.
В таблице 1.3 медианным является среднее из 143 значений, т. е. семьдесят второе от начала ряда значение уровня преступности. Как видно из ряда накопленных частот, оно находится в четвертом интервале. Тогда, применяя приведенную выше формулу, получим Ме = 295 преступлений на 100 тыс. чел.
В дискретном вариационном ряду медианой следует считать значение признака в той группе, в которой накопленная частота превышает половину численности совокупности. Например, для данных таблицы 1.2 медианой числа задержанных разыскиваемых лиц за одну операцию по розыску будет 2.
Аналогично медиане вычисляются значения признака, делящие совокупность на четыре равные по числу единиц части. Эти величины называются квартилями и обозначаются заглавной латинской буквой Q с индексом – номером квартиля (Q1, Q2, Q3). Ясно, что Q2 совпадает с Me.
Значения признака, делящие ряд на пять равных частей, называют квинтилями, на десять частей – децилями, на сто частей – перцентилями.
12
Бесспорно, важное значение имеет такая величина признака, которая встречается в изучаемом ряду в совокупности чаще всего. Такую величину, как уже отмечалось выше, именуют модой и обозначают Мо. В дискретном ряду мода определяется без вычисления как значение признака с наибольшей частотой. Например, по данным таблицы 1.2 чаще всего (а именно 71 раз) в операции по задержанию лиц, объявленных в розыск, задерживалось по 2 лица, т. е. модой является число 2. Обычно встречаются ряды с одним модальным значением признака. Если два равных значения признака имеются в вариационном ряду, он считается, соответственно, бимодальным (если несколько – мультимодальным). Наличие в распределении более одной моды указывает на неоднородность совокупности, возможно, представляющей собой смесь нескольких разнородных совокупностей, соответственно с разными модами.
Следующим этапом изучения вариации признака в совокупности является измерение характеристик силы, величины вариации. Простейшей из таких характеристик служит размах (или амплитуда вариации, изменения) – абсолютная разность между максимальным и минимальным значениями признака изучаемого ряда (совокупности) значений. По сути, это величина диапазона имеющихся значений. Таким образом, размах вычисляется по формуле:
R = Хmax – Хmin.
Поскольку размах по своему определению измеряет максимальное различие значений признака, он не способен характеризовать, отражать закономерную силу его вариации во всей совокупности. Предназначенный для данной цели показатель должен учитывать и обобщать все различия значений признака в совокупности без исключения. Число таких различий велико. Так, для примера, описанного в таблице 1.3, оно составит 10 153 (это число рассчитывается как число сочетаний по два из всех единиц сово-
купности (C2143)).
Однако в этом примере нет необходимости рассматривать, вычислять и усреднять все отклонения. Проще использовать среднюю величину из величин отклонений отдельных значений признака от среднего арифметического значения признака (каковых 143). Но среднее отклонение значений признака от средней арифметической величины, согласно известному свойству последней, равно нулю. Поэтому показателем силы вариации выступает не алгебраическая средняя отклонений, а средний модуль (среднее абсолютное значение) отклонений:
13
 .
.
По данным таблицы 1.3 средний модуль, или среднее линейное отклонение, по абсолютной величине вычисляется как взвешенное по частоте отклонение по модулю середин интервалов от средней арифметической величины, т. е. по формуле:
 = 68,5 прест. на 100 тыс. чел.
= 68,5 прест. на 100 тыс. чел.
Это означает, что в среднем уровень преступности в изучаемой совокупности населенных пунктов отклонялся от уровня преступности по области на 68,5 преступлений на 100 тыс. чел. Простота самого расчета и осмысления такого расчета (простота интерпретации) представляют положительные стороны данного показателя. Однако модуль нельзя поставить в соответствие с каким-либо вероятностным законом (статистическим распределением), в том числе и с нормальным распределением, параметром которого является не средний модуль отклонений, а среднее квадратическое отклонение (в компьютерных программах это по-английски называется «the standard deviation», сокращенно «s. d.» или же просто «s», а порусски – СКО). В статистической литературе среднее квадратическое отклонение от средней величины принято обозначать малой (строчной) греческой буквой σ (читается «сигма»), если речь идет о теоретической величине, или же s (когда речь идет о приближенной оценке для σ).
Для ранжированного ряда:
 ,
,
для интервального ряда:
 .
.
По данным таблицы 1.3 среднее квадратическое отклонение уровня преступности составило 84,4 преступления на 100 тыс. чел.
Среднее квадратическое отклонение по величине в реальных совокупностях всегда больше среднего модуля отклонений.
14
Квадрат среднего квадратического отклонения σ2 дает величину, именуемую дисперсией. Формула дисперсии:
простая (для не сгруппированных внутри интервалов используемых данных):
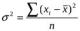 ,
,
или взвешенная (для сгруппированных данных):
 .
.
1.2. Пример решения типовой задачи
Рассмотрим, например, показатель «Преступления, совершенные в районах города».
Таблица 1.5
Преступления, совершенные в районах города Петровска
|
Коли- |
|
Наименование |
Относит. уровень |
|
Наименова- |
чество |
|
ОВД, упорядо- |
преступности |
|
пре- |
№ |
ченных по относи- |
в городах (кол-во |
||
ние ОВД |
|||||
ступле- |
|
тельному уровню |
преступлений |
||
|
|
||||
|
ний |
|
преступности |
на 100 тыс. чел.) |
|
|
|
|
|
|
|
Алексеев- |
1854 |
1 |
Сурожский |
9,71 |
|
ское |
|||||
|
|
|
|
||
|
|
|
|
|
|
Вяземский |
1011 |
2 |
Павловский |
10,90 |
|
|
|
|
|
|
|
Гороховский |
240 |
3 |
Медведевское |
12,16 |
|
|
|
|
|
|
|
Гусевское |
2083 |
4 |
Косинский |
13,11 |
|
|
|
|
|
|
|
Каменский |
294 |
5 |
Вяземский |
13,68 moda |
|
|
|
|
|
|
|
Качинский |
510 |
6 |
Сусанинский |
13,68 |
|
|
|
|
|
|
|
Киреевское |
2884 |
7 |
Гороховский |
13,71 |
|
|
|
|
|
|
|
Косинский |
679 |
8 |
Каменский |
13,74 mediana |
|
|
|
|
|
|
|
Макаров- |
289 |
9 |
Качинский |
13,97 mediana |
|
ский |
|||||
|
|
|
|
||
|
|
|
|
|
|
Медведев- |
1759 |
10 |
Макаровский |
15,97 |
|
ское |
|||||
|
|
|
|
||
|
|
|
|
|
|
Павловский |
645 |
11 |
Алексеевское |
16,55 |
|
|
|
|
|
|
|
Сергеевский |
225 |
12 |
Киреевское |
16,94 |
|
|
|
|
|
|
|
Собинов- |
913 |
13 |
Юрьевский |
18,06 |
|
ский |
|||||
|
|
|
|
||
|
|
|
|
|
|
Сурожский |
232 |
14 |
Собиновский |
18,22 |
|
|
|
|
|
|
|
Сусанин- |
223 |
15 |
Гусевское |
18,72 |
|
ский |
|||||
|
|
|
|
||
|
|
|
|
|
|
Юрьевский |
390 |
16 |
Сергеевский |
21,23 |
|
|
|
|
|
|
Мода (Мо) – наиболее часто встречающееся значение ряда. В приведенном ряду значений, нормированных по численности
16
населения, как правило, моды быть не может (мода вырожденная), т. к. каждое значение встречается всего лишь по одному разу. Хотя
вданном случае в качестве моды указано значение 13,68, это значение, на самом деле, представляет собой с определенной точностью округление, удовлетворяющее по точности цели проводимого анализа. Строго говоря, никакие пары исходных (неокругленных) значений не совпадают: так, при округлении с большей точностью Вяземский ГОВД имеет значение, равное 13.680649, а Сусанинский РОВД – 13.680981, т. е. хоть ненамного, но больше. Поскольку для цели данного анализа такая повышенная точность не имеет никакой роли, заключение (вывод) о равенстве либо неравенстве значений производится уже на основе округленных значений.
Итак, исходные данные, нормированные по населению, не обладают модой (или, что фактически то же самое, формально каждое значение может считаться модой). Но такие данные можно предварительно сгруппировать и рассматривать моду уже группированных данных. Для этого выберем диапазон данных, включающий все имеющиеся данные. В качестве границ диапазона на числовой оси удобно выбрать значения достаточно круглые и ближайшие к крайним (наибольшему и наименьшему значениям исходных данных). При этом нижняя граница избирается как достаточно круглое значение, меньше меньшего значения анализируемых данных, а верхняя – больше большего. Конкретно в рассматриваемом случае анализируемые данные варьируются (изменяются) в пределах от 9,71 до 21,23, и за соответствующие им круглые значения диапазона можно принять 9,5 и 21,5.
Примечание. Конечно, можно избрать и такие границы диапазона, как, например, 9,0 и 22,0, значения которых еще более круглые и потому, казалось бы, более удобные. Это, однако, не так. Выбор указанных значений границ обусловлен двумя обстоятельствами: во-первых, диапазон в этих границах минимален, жестко охватывает реальные данные. Во-вторых, он равен 12, т. е. может быть разбит и на два, и на три, и на четыре, и даже на шесть равных интервалов без остатка, что представляет дополнительное удобство при визуальном анализе, поскольку границы интервалов при этом также будут числами круглыми. Разумеется, для результатов компьютерного анализа округлость граничных значений не играет никакой роли, но дробные значения несколько затрудняют восприятие их человеком. Кроме того, число интервалов должно быть примерно в несколько раз меньше, чем число данных
вряде. В зависимости от количества интервалов, на которые разбивается диапазон значений, результаты могут по-разному восприниматься, поэтому порой следует рассмотреть не один вариант подобного разбиения. Рассмотрим ряд таких разбиений имеющегося диапазона
17
размером 12. Договоримся здесь считать правую границу включенной в интервал, а левую, соответственно, не включенной в него (вообще, можно включать и наоборот, лишь бы никакое граничное значение не оказалось учтенным дважды – и в одном, и в другом интервале).
Диапазон разбит на 6 равных интервалов. Тогда получаем следующую картинку-график, которую именуют гистограммой (иными словами: эмпирическим статистическим распределением данных по рассматриваемому показателю):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
12 |
|
15 |
|
|
|
|
|
|
|
2 |
|
4 |
|
|
6 |
|
11 |
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
3 |
|
|
5 |
|
10 |
|
13 |
|
16 |
|
|
|
|
|
9,5 |
11,5 |
13,5 |
Мо 15,5 |
17,5 |
19,5 |
21,5 |
|
||||||||
Номера значений в гистограмме, как правило, не проставляют, здесь же они даны для наглядности и удобства дальнейшего анализа. Сами значения в гистограмме уже утрачивают свою точность – их рассматривают лишь с точностью до интервала, в который они попали, т. е. до группы, задаваемой этим интервалом. О двух минимальных значениях районов области из гистограммы известно, что они между 9,5 и 11,5; два последующих – между 11,6 и 13,5; пять значений – между 13,5 и 15,5; три значения – между 15,5 и 17,5; три значения – между 17,5 и 19,5; одно – между 19,5 и 21,5. Здесь наиболее часто (в 31 % случаев) встречается вариант: интервал между 13,5 и 15,5 (границы модального интервала иногда для простоты заменяют с некоторой неизбежной потерей информации о характере распределения на значение его середины – 14,5).
Вот иные варианты разбиения диапазона на интервалы. Вариант: четыре интервала с длиной, соответственно, 12/4=3:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
14 |
|
|
|
|
|
|
|
|
|
|
7 |
|
|
13 |
|
|
|
|
|
|
|
|
3 |
|
6 |
|
|
12 |
|
|
|
|
|
|
|
|
2 |
|
5 |
|
|
11 |
|
|
16 |
|
|
|
|
|
1 |
|
4 |
|
|
10 |
|
|
15 |
|
|
|
9,5 |
12,5 |
Мо |
15,5 |
17,5 |
18,5 |
21,5 |
|||||||
18
При таком разбиении значение моды, определяемое значением, встречающимся в 37,5 % случаев, таково: интервал между 12,5 и 15,5 (середина модального интервала – 14).
Вариант: три интервала с длиной, соответственно, 12/3=4:
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
4 |
|
8 |
|
|
16 |
|
|
|
3 |
|
7 |
|
|
15 |
|
|
|
2 |
|
6 |
|
|
14 |
|
|
|
1 |
|
5 |
|
|
13 |
|
|
|
9,5 |
13,5 |
Мо |
17,5 |
21,5 |
|||
При таком разбиении значение моды, определяемое значением, встречающимся в 50 % случаев, таково: интервал между 13,5 и 17,5 (середина модального интервала – 15,5).
Вариант: восемь интервалов с длиной, соответственно, 12/8=1,5:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
5 |
|
|
|
|
11 |
|
14 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
3 |
|
4 |
|
|
|
|
10 |
|
13 |
|
15 |
|
16 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
9,5 |
11,0 |
12,5 |
14,0 |
15,5 |
17,0 |
18,5 |
20,0 |
21,5 |
|
|
|
|||||||||||
При таком разбиении значение моды, определяемое значением, встречающимся в 37,5 % случаев, таково: интервал между 12,5 и 14,0 (середина модального интервала – 13,25).
Вариант: двенадцать интервалов с длиной, соответственно, 12/12=1:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
12 |
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
|
|
|
|
10 |
|
11 |
|
13 |
|
15 |
|
|
|
16 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9,5 |
10,5 |
11,5 |
12,5 |
13,5 |
14,5 |
15,5 |
16,5 |
17,5 |
18,5 |
19,5 |
20,5 |
21,5 |
|
||||||||||||||||
19
При таком разбиении значение моды, определяемое значением, встречающимся в 31 % случаев, таково: интервал между 13,5 и 14,5 (середина модального интервала – 14,0).
Вариант: два интервала с длиной, соответственно, 12/2=6:
|
|
|
|
|
|
9 |
|
|
|
|
|
8 |
|
|
|
|
|
7 |
|
16 |
|
|
|
6 |
|
15 |
|
|
|
5 |
|
14 |
|
|
|
4 |
|
13 |
|
|
|
3 |
|
12 |
|
|
|
2 |
|
11 |
|
|
|
1 |
|
10 |
|
|
|
9,5 |
15,5 |
21,5 |
|
||
При таком разбиении значение моды, определяемое значением, встречающимся в 56,25 % случаев, таково: интервал между 9,5 и 15,5 (середина модального интервала – 12,5).
Медиана представляет вид среднего, которое типично в том смысле, что значение объекта, признанное медианным, таково, что меньше его ровно столько же значений, сколько и тех, что больше его. Особенность медианы в сравнении с прочими видами средних в том, что всегда найдется реальный объект с такими значениями (при других средних это в большинстве случаев расчетное значение).
Медиана (Ме) определяется как значение члена числового ряда, стоящего в его середине, если число членов ряда нечетно. Формула для номера члена ряда с нечетным числом членов такая: №Me = (n+1)/2. Например, если n = 15, то №Me = 8. Если число членов четное, то берется полусумма двух подряд идущих членов ряда с номером № = (n+1)/2 и соответственно, № = (n+1)/2+1. В данном случае n = 16, поэтому №Me = 8 и 9, а сама медиана Me = (13,74 + +13,97) = 13,86.
Примечание. Когда ряд ранжирован, но при этом он не количественной, а качественной природы (порядковая шкала измерения – «больше – меньше», «хуже – лучше» и т. п.), когда операции и сложения, и деления попросту отсутствуют, при нечетном числе членов применима указанная выше формула. А при четном числе членов ранжированного ряда в качестве медианы из двух рядом стоящих возможных значений выбирается то, на которое укажет какой-либо «механизм случайных чисел» (например, монета, которую подбра-
20
