Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный институт электроники и математики (технический университет)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

vince_j_quaternions_for_computer_graphics

.pdf

Скачиваний:

118

Добавлен:

08.02.2015

Размер:

3.44 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 1614 15 16 > Следующая >>>

116

Quaternions in Space

For q1:

√

s =

x = 0,

y =

z = 0

which when substituted in (7.15) gives

2(s2

x2)

−

2(xz + sy)

2(xy

− sz)

2(xy

sz)

2(s + y ) − 1

2(yz − sx)

2(xz

+ sy)

2(yz

sx)

2(s2

z2)

−

yp .

(7.22)

= −1 0 0 zp

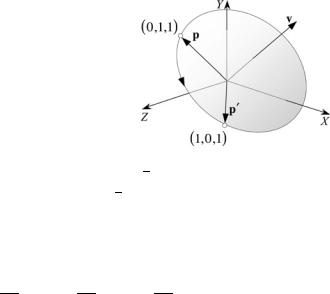
Substituting the coordinates (0, 1, 1) in (7.22) gives

1 0 1 0 1

which is correct.

0 = −1 0 0 1

For q2:

√

s =

x =

= 0,

z = 0

which when substituted in (7.15) gives

2(s2

x2)

−

2(xz + sy)

2(xy

− sz)

2(xy

sz)

2(s + y ) − 1

2(yz − sx)

2(xz

+ sy)

2(yz

sx)

2(s2

z2)

−

yp .

−1

(7.23)

Substituting the coordinates (0, 1, 1) in (7.23) gives

−1

0 0 −1

1 0 1 0 1

which is also correct.

Using (7.20) with t = 0.5 computes a mid-way position for an interpolated

quaternion, with its vector at 45° between the x- and y-axes, as shown in Fig. 7.13.

We already know that θ = 60°, therefore sin θ =

√

3/2:

sin(1 − t )θ

sin t θ

sin θ

+ sin θ

sin 1 60°

√

sin 1 60°

√

j +

sin 60°

7.9 Interpolating Quaternions

117

Fig. 7.13 The point (0, 1, 1) is rotated 90° about the vector v to (1, 0, 1)

									√					√											√			√
=			1							2			,		2		j						1		2	,			2			i
										2					2										2				2
										2					2										2				2
		√3														+							√3
			√							1							1				j
							2	,		1				i	+		1
								,						i
=				√			3				√	6					√		6
where	√
	√															1												1
s =					2											1												1
		√				,								x =				√				,		y =			√				, z = 0
		√			3	,								x =				√		6		,		y =			√			6	, z = 0

which when substituted in (7.15) gives																		+
	2(s2	+	x2)		−			2		2								+
p =	2(s2		x2)			1	2(xy − sz)								2(xz				sy)			xp
p =	2(xy + sz)						2(s + y ) − 1								2(yz − sx)						1	yp
	2(xz		−	sy)			2(yz			+	sx)			2(s2			+	z2)		−	1	zp
	2		−							+							+			−
	2	1			2		xp	.
	1	2			32		xp
=	3	3		− 3		yp
	3	3
	3	3					zp
	2	2			1		zp
	− 3	3			3
Substituting the coordinates (0, 1, 1) in (7.24) gives
					1			2		1		2				0
					1			1		2		−	2			0
					0 =			3		3		−	3			1
								3		3		3
					1				2	2		1				1
							−		3	3		3

(7.24)

(7.25)

which gives the point (1, 0, 1).

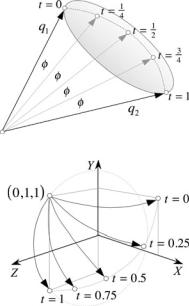
One of the reasons for using a spherical interpolant is that it linearly interpolates the angle between the two unit-norm quaternions, which creates a constant-angular velocity between them. However, one of the problems with visualising quaternions is that they reside in a four-dimensional space and create a hyper-sphere with a radius equal to the quaternion’s norm. With our 3D brains, this is difﬁcult to visualise. Nevertheless, we can convince ourselves into thinking we see what is going on with a simple sketch, as shown in Fig. 7.14, where we see part of the hyper-sphere and two quaternions q1 and q2. In this example, the angle φ is a constant angle between two values of the interpolant t . The spherical interpolant also ensures that the norm

118	7 Quaternions in Space

Fig. 7.14 Spherical interpolation between q1 and q2

Fig. 7.15 Sketch showing the actions of the interpolated quaternions

of the interpolated quaternion remains constant at unity, preventing any unwanted scaling.

Figure 7.15 provides another sketch to help visualise what is going on. For example, when t = 0, the interpolated quaternion is q1 which rotates the point (0, 1, 1) to (1, 1, 0), and when t = 1, the interpolated quaternion is q2 which rotates the point (0, 1, 1) to (0, −1, 1). When t = 0.5, the interpolated quaternion rotates the point (0, 1, 1) to (1, 0, 1) as computed above. Two other curves show what happens for t = 0.25 and t = 0.75.

A natural consequence of the interpolant is that the angle of rotation is 90° for t = 0 and t = 1, but for t = 0.5 the angle of rotation (eigenvalue) is approximately 70.5°. Corresponding angles arise for other values of t .

7.10 Converting a Rotation Matrix to a Quaternion

The matrix transform equivalent to qpq−1 is

qpq−

2(s2

+ x2) − 1

2(xy − sz)

2(xz

sy)

2(xy

sz)

2(s

) − 1

+ y

2(yz − sx)

2(xz + sy)

2(yz

sx)

2(s2

z2)

−

a21

a22

a23

yp .

a11

a12

a13

= a31

a32

a33 zp

7.10 Converting a Rotation Matrix to a Quaternion

119

Inspection of the matrix shows that by combining various elements we can isolate the terms of a quaternion s, x, y, z. For example, by adding the terms a11 + a22 + a33 we obtain

a11 + a22 + a33 = 2 s2 + x2 − 1 + 2 s2 + y2 − 1 + 2 s2 + z2 − 1

=6s2 + 2 x2 + y2 + z2 − 3

=4s2 − 1

therefore,

s = ± 1 + a11 + a22 + a33.

To isolate x, y and z we employ

x = 1 (a32 − a23)

y = 1 (a13 − a31)

z = 1 (a21 − a12).

We can conﬁrm their correctness using the matrix (7.25):

				a11				a12		a13				2			1			2		2
				a11				a12		a13				1			2				−	2
				a21				a22		a23 =				3			3				−	3
														3			3			3
				a31				a32		a33				2			2			1
														− 3			3			3
		1												1		1		2				2 1
s		1		1	a11				a22		a33			1				2				2 1

	= ±		2				+			+		= ±		2			+		3	+			3 +	3		=
	= ±		2	+			+			+		= ±		2			+		3	+			3 +	3		=
				x = 4s (a32 − a23) =													3 +			3			= √
				x = 4s (a32 − a23) =									√				3 +			3			= √
						1							√3				2			2				1
													4
													4		2										6
				y = 4s (a13 − a31) =													3 +			3			= √
				y = 4s (a13 − a31) =									√				3 +			3			= √
						1							√3				2			2				1
													4
													4		2										6
				z = 4s (a21 − a12) =													3 −			3			= 0
				z = 4s (a21 − a12) =									4√2				3 −			3			= 0
					1								√3				1			1

√

√2 3

which agree with the original values.

Say, for example, the value of s had been close to zero, this could have made the values of x, y, z unreliable. Consequently, other combinations are available:

x = ± 1 + a11 − a22 − a33

y = 1 (a12 + a21)

z = 1 (a13 + a31)

120 7 Quaternions in Space

s = 1 (a32 − a23)

y = ± 1 − a11 + a22 − a33

x = 1 (a12 + a21)

z = 1 (a23 + a32)

s = 1 (a13 − a31)

z = ± 1 − a11 − a22 + a33

x = 1 (a13 + a31)

y = 1 (a23 + a32)

s = 1 (a21 − a12).

7.11 Euler Angles to Quaternion

In Chap. 6 we discovered that the rotation transforms Rα,x , Rβ,y and Rγ ,z can be combined to create twelve triple combinations to represent a composite rotation. Now let’s see how such a transform is represented by a quaternion.

To demonstrate the technique we must choose one of the twelve combinations, then the same technique can be used to convert other combinations. For example, let’s choose the sequence Rγ ,z Rβ,y Rα,x where the equivalent quaternions are

qx =

qy =

qz =

and

Expanding (7.26):

cos	2	α, sin	2	αi
	1		1
cos	2	β, sin	2	βj
	1		1
cos	2	γ , sin	2	γ k
	1		1
q = qzqy qx .				(7.26)

7.11 Euler Angles to Quaternion								βj cos				121
q =	cos 2	γ , sin	2	γ k cos	2	β, sin	2	βj cos	2	α, sin	2	αi
	1		1		1		1		1		1

=cos γ cos β,

cos	2		γ sin			2		βj + cos										2	β sin				2			γ k − sin										2	γ sin				2	βi cos						2	α, sin				2	αi
	1					1												1					1													1					1							1					1
= cos		2		γ cos				2			β cos				2		α + sin							2			γ sin						2	β sin				2	α,
		1						1							1									1									1					1
cos	1		γ cos			1				β sin			1		αi + cos								1				α cos						1	γ sin				1	βj + cos						1	α cos					1	β sin			1	γ k

	2					2							2										2										2					2							2						2				2
− cos				2	α sin					2		γ sin				2		βi − cos									2		γ sin					2		β sin			2		αk + cos						2	β sin				2	γ sin			2	αj
			1							1						1											1							1					1								1					1				1
= cos
= cos		2		γ cos				2			β cos				2		α + sin							2			γ sin						2	β sin				2	α,
		1						1							1									1									1					1
cos			2	γ cos				2			β sin			2			α − cos							2				α sin					2	γ sin				2	β			i
			1						1					1										1									1					1
cos				α cos							γ sin						β + cos											β sin						γ sin						α		j
cos			2	α cos					2		γ sin			2			β + cos							2				β sin					2	γ sin				2		α		j
			1					1						1										1									1					1
cos				α cos							β sin						γ − cos											γ sin							β sin					α		k .
cos			2	α cos					2		β sin			2			γ − cos								2			γ sin					2		β sin			2		α		k .
			1					1						1										1									1					1
Now let’s place the angles in a consistent sequence:
							s = cos							1		γ cos					1		β cos							1		α		+ sin				1		γ sin			1	β sin				1		α

														2							2									2								2					2					2
					xq = cos									1		γ cos					1		β sin							1	α − sin							1	γ sin				1	β cos				1		α

														2							2									2								2					2					2
					yq = cos									1		γ sin					1	β cos								1	α + sin							1	γ cos				1	β sin				1		α

														2							2									2								2					2					2
					zq = sin								1			γ cos					1	β cos								1	α − cos							1		γ sin			1	β sin				1		α

													2								2									2								2					2					2
where
																		q = [s, xq i + yq j + zq k].																																						(7.27)
Let’s test (7.27). We start with the three rotation transforms
															Rα,x									0					cos α − sin α
																				=				1							0							0
														Rβ,y						=				0					sin α								cos α
														Rβ,y															0					1				0
																										cos β								0			sin β
																				= − sin β														0			cos β

122 7 Quaternions in Space

Rγ ,z	sin γ		cos γ	0	.
	=	cos γ	− sin γ	0
	=	0	0	1

Then

Rγ ,zRβ,y Rα,x																															sin γ sin α + cos γ sin β cos α
cos γ cos β − sin γ cos α + cos γ sin β sin α																															sin γ sin α + cos γ sin β cos α								.
= sin γ cos β		cos γ cos α + sin γ sin β sin α																												− cos γ sin α + sin γ sin β cos α									.
− sin β											cos β sin α																									cos β cos α
Let’s make α = β = γ = 90°, then																											0				0		1
																											0				0		1
		R90°,zR90°,y R90°,x																									0				1		0
																						= −1									0		0
which rotates points 90° about the y-axis:
								1								0							0		1						0	.
								1								0 1 0															1	.
								0		=						−1 0 0															1
Now let’s evaluate (7.27):
s = cos					1		γ cos						1		β cos				1			α			+ sin			1			γ sin			1		β sin	1	α

					2								2							2								2						2			2
	√				√				√							√				√ √
=	2						2			2				+		2							2		2

	2						2			2						2					2				2
	√
=	√		2
=		2			1								1						1									1						1			1
xq = cos					1		γ cos						1		β sin				1		α			− sin				1	γ sin					1	β cos		1	α

					2								2						2									2						2			2
= 0					1								1						1									1						1			1
yq = cos					1		γ sin						1	β cos					1		α			+ sin				1	γ cos					1		β sin	1	α

					2								2						2									2						2			2
	√				√				√							√			√2 √
=	√		2		√			2	√			2		+		√	2		√2 √							2
=		2					2				2			+		2					2				2
	√
=	√		2

		2		1									1						1									1						1			1
zq = sin				1		γ cos							1	β cos					1		α			− cos				1			γ sin			1		β sin	1	α

				2									2						2									2						2			2
= 0
and																√								√
																√								√
													q =					2					,		22 j
													q =					2					,		22 j

which is a quaternion that also rotates points 90° about the y-axis.

7.12 Summary

123

7.12 Summary

This chapter has been the focal point of the book where unit-norm quaternions have been used to rotate a vector about a quaternion’s vector. It would have been useful if this could have been achieved by the simple product qp, like complex numbers. But as we saw, this only works when the quaternion is orthogonal to the vector. The product qpq−1—discovered by Hamilton and Cayley—works for all orientations between a quaternion and a vector. It is also relatively easy to compute. We also saw that the product can be represented as a matrix, which can be integrated with other matrices.

Perhaps one of the most interesting features of quaternions that has emerged in this chapter, is that their imaginary qualities are not required in any calculations, because they are embedded within the algebra.

The spherical interpolant provides a clever way to dynamically change a quaternion’s axis and angle of rotation, but can be difﬁcult to visualise as an animated sequence without access to a real-time display system.

The reverse product q −1pq reverses the angle of rotation, and is equivalent to changing the sign of the rotation angle in qpq−1. Consequently, it can be used to rotate a frame of reference in the same direction as qpq−1.

7.12.1 Summary of Operations

Rotating a point about a vector

q = [s, v]

s2 + |v|2 = 1

p = [0, p]

qpq−1 = 0, 2(v · p)v + 2s2 − 1 p + 2sv × p

q =

cos 2

θ , sin

θ vˆ

p = [0, p]

qpq−1 = 0, (1 − cos θ )(vˆ · p)vˆ + cos θ p + sin θ vˆ × p

Rotating a frame about a vector

q−1pq = 0, (1 − cos θ )(vˆ · p)vˆ + cos θ p − sin θ vˆ × p

Matrix for rotating a point about a vector

−

2(y2

+ z2)

2(xy − sz)

2(xz + sy)

p =

1 − 2(x

+ z

)

2(yz − sx)

2(xy + sz)

2(xz

−

sy)

2(yz

sx)

−

2(x2

y2)

124

Quaternions in Space

Matrix for rotating a frame about a vector

−

2(y2

z2)

2(xz − sy)

p =

2(xy

+ sz)

2(xy − sz)

1 − 2(x + z )

2(yz + sx)

2(xz

sy)

2(yz

−

sx)

−

2(x2

Matrix for a quaternion product

−z1

q1q2

L(q1)q2

−x1

−y1

−z1

= y1

−x1

−

−y2

R(q2)q1

−x2

−y2

= y2

−z2

q1q2

−

Interpolating two quaternions

sin(1 − t )θ q

sin t θ q

sin θ

where

cos θ

q1 · q2

|q1||q2|

s1s2 + x1x2 + y1y2 + z1z2

|q1||q2|

Quaternion from a rotation matrix

s = ± 1 + a11 + a22 + a33

x = 1 (a32 − a23)

y = 1 (a13 − a31)

z = 1 (a21 − a12)

x = ± 1 + a11 − a22 − a33


y =	1		(a12		+ a21)
	4x
z =	1		(a13		+ a31)

	4x
s =	1		(a32		− a23)

	4x
	1

y = ±				1	− a11 + a22 − a33
		2

7.13 Worked Examples																								125
			x =		1						(a12		+ a21)

					4y
				z =	1						(a23		+ a32)

					4y
				s =	1						(a13		− a31)

					4y
							1
							1					1	− a11 − a22 + a33
				z = ±
				z = ±					2
			x =		1					(a13			+ a31)

					4z
			y =		1					(a23			+ a32)

					4z
				s =	1					(a21			− a12)

					4z
Eigenvector and eigenvalue
		xv = (a22 − 1)(a33 − 1) − a23a32
		yv = (a33 − 1)(a11 − 1) − a31a13
			zv = (a11 − 1)(a22 − 1) − a12a21
					1
cos θ =								Tr qpq−1 − 1
cos θ =						2		Tr qpq−1 − 1
Euler angles to quaternion
Using the transform Rγ ,z Rβ,y Rα,x :
s = cos	1			γ cos			1					β cos		1		α + sin	1		γ sin	1		β sin	1	α

	2						2							2			2			2			2
xq = cos	1			γ cos			1					β sin		1	α − sin		1	γ sin		1	β cos		1	α

	2						2							2			2			2			2
yq = cos	1			γ sin			1				β cos			1	α + sin		1	γ cos		1		β sin	1	α

	2						2							2			2			2			2
zq = sin	1		γ cos				1				β cos			1	α − cos		1		γ sin	1		β sin	1	α

	2						2							2			2			2			2

where

q= [s, xq i + yq j + zq k].

7.13Worked Examples

Here are some further worked examples that employ the ideas described above.

Example 1 Use qp to rotate p = [0, j] 90° about the x-axis.

For this to work q must be orthogonal to p:

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 1614 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.11.2019146.94 Кб6training.doc
#
08.02.2015491.01 Кб6Uchebnoe_posobie_GMBSS_VFPS.doc
#
08.02.20151.53 Mб3UNIVER_30_08.pdf
#
04.08.2019212.48 Кб2var_test._zadanii-1.doc
#
20.04.2019215.04 Кб1var_test._zadanii-2.doc
#
08.02.20153.44 Mб118vince_j_quaternions_for_computer_graphics.pdf
#
21.11.20193.06 Mб2workbook-infcs-labs.doc
#
08.02.2015264.7 Кб5zachet_ekonom (1).doc
#
08.02.2015418.97 Кб10_Лр_2012.pdf
#
08.02.2015294.4 Кб9Алгоритмизация вычислений НИУ ВШЭпрогр 2014_15.doc
#
08.02.2015211.45 Кб16Архитектура ЭВМ - испр.docx