Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2563.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

18.1 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

Окончание табл. 3.1

1	2	3	4	5	6
	189			5,56	38,68
48	190	3	1,6	5,65	39,65
48	191	3	1,6	5,65	39,65
	191			5,65	39,65
	192			5,65	39,65
	193			5,51	38,1
49	194	3	1,6	5,56	38,68
49	195	3	1,6	5,65	39,65
	195			5,65	39,65
	196			5,65	39,65
	197			5,76	39,1
50	198	3	1,7	5,76	39,1
50	199	3	1,7	5,76	39,1
	199			5,76	39,1
	200			5,76	39,1

Аналогичные выборки из 200 частных значений углов рассеивания напряжений сформированы для каждой разновидности, испытанных песков и глинистых грунтов.

3.2. Обработка данных методами математической статистики

Частные значения углов рассеивания напряжений являются случайной величиной. В теории вероятностей математическое описание случайных величин выполняется при помощи законов их распределения [8, 10, 25]. Под законом распределения случайной величины понимают любое соотношение, устанавливающее связь между значениями случайной величины и вероятностью их появления. В табл. 3.2 приведены классические и наиболее распространенные функции непрерывных распределений и плотности вероятности случайной величины.

Таблица 3.2. Функции распределения и плотности вероятности

непрерывной случайной величины


Тип	Функции распределения F и плотности вероятности f
1	2
	F x		x a	при a x b,
			b a

Равномерное распре-	где а и b – границы интервала, в пределах которого рас-
деление [1, с. 178]	пределена непрерывная случайная величина х (b>а).
	f x	1		; при a x b
		b a

110

Продолжение табл. 3.2

F x

ехр

x Мх

dx; при - х ,

где – среднеквадратическое отклонение; Мх – матема-

тическое ожидание.

В функции F(x) выполняется замена переменных

Нормальное

рас-

t x Мх ;

dx dt. После чего F(x) дают в виде

пределение [1, 8]

F x

ехр

dt ;

f x

ехр

;

f x

х Мх

ехр

ln х Мх

Логарифмическое

F x

erf

;

нормальное распре-

деление [1, с. 175]

f x

ехр

lnх Мх

при x>0

F x

Г п 1 /2

F1 0,5;

п 1

/2;1,5; х2 /п ,

Распределение

п Г п/2

Уи́ льяма

Си́гдели Г – гамма-функция Эйлера; F1 – гипергеометрическая

Го́ ссета(Стьюдента)

функция

Г п 1 /2

[1, с. 193]

f x

п 1 / 2

п Г п/2 1 х2

/п

Распределение

Па-

F x 1 a/x k ; при а х ; а>0; k>0,

где а – коэффициент сдвига.

рето [1, с. 185]

f x k ak x k 1

x a

F x

arctg

; при - х ; >0,

Распределение

Ко-

ши

где а – коэффициент сдвига; – коэффициент масштаба

[1, с. 186]

f x

x a / 2

Экспоненциальное

F x 1 ехр а х ,

распределение

где а – параметр распределения (a>0).

[1, с. 186]

f x a ехр a x ; при x 0

111

Продолжение табл. 3.2

F x

exp x α ;

x a

exp x α ;

Распределение Лап-

F x 1

x a,

ласа [57]

где а – коэффициент сдвига; – коэффициент масштаба

f x

exp

x a

F x 2Ф

ехр

;

2 a

Распределение Мак-

f x

ехр

; при x>0

свелла [57]

2 a

Мx 0,6267 Мx

k 1 a x n

F x 1 exp a x

ехр a x ; при x 0,

Распределение

Эр-

n 1 n!

где a и k – параметры распределения (a 0), (k=1, 2, 3 …)

ланга [57]

f x

a a x k 1

ехр a x

k 1!

F x 1 ехр

; при x 0,

Распределение Вей-

булла

(двухпара-

где – параметр формы распределения >0; – параметр

метрическое) [1, с.

масштаба распределения >0.

183]

f x

ехр

F x 1 ехр

; при x 0,

Распределение Вей-

булла (трехпарамет-

где – параметр местоположения распределения х.

рическое)

f x

ехр

Гамма-

f x

k 1

ехр x ,

распределение,

или

Г k

Г-распределение

[1,

где k – коэффициент k >0; – параметр масштаба распре-

с. 199]

деления >0

112

Окончание табл. 3.2

1					2
Гамма-		F x	k, 2				; при x>0
распределение,	или
распределение,	или
Г-распределение	[1,		xk 1 exp x dx
с. 199]		0
					k 1	k a x n
Распределение	F x 1 exp k a x							ехр a x ;
	F x 1 exp k a x							ехр a x ;
	Эр-				n 1	n!
ланга нормирован-		k a k a x		k 1
ное [57]	f x	k a k a x			ехр k a x ; при x 0,
	f x	k 1!			ехр k a x ; при x 0,
		k 1!

где a и k – параметры распределения (a 0), (k=1, 2, 3 …)

f x qi 1 ехр ai x ; при x 0,

i 1

где i и п – номер и общее число генераторов экспоненци-

ально распределенных случайных величин; qi – вероят- Гиперэкспоненци- ность вырабатывания i-м генератором только одной слу- альное распределе- чайной величины ( qi=1); ai – параметр распределения, с

ние [57]

которым вырабатывается случайная величина i-м генератором (ai>0).

f x qi ai ехр ai x

i 1

Некоторые частные значения углов рассеивания напряжения, рассчитанные по измеренным диаметрам дефектов на различной глубине, отличаются на сотые доли градусов. Такая малая разница может быть обусловлена ошибкой измерений, например глубины заложения вкладыша, определяемой при помощи металлической линейки с точностью до 1 мм, что вносит некоторые незначительные искажения в результаты вычисления углов рассеивания в моделях с вкладышами на различной глубине. Поэтому такие значения округлены до десятых градуса. На первом этапе статистической обработки результаты эксперимента представляются в виде вариационного ряда, в котором измеренные числовые характеристики представляются в порядке возрастания или убывания с характерной частотностью [33].

Частота числовой характеристики определяется по формуле

f	n	,	(3.2)

	n

где n и n – количество совпадений характеристики и общее число измерений.

В табл. 3.3 приведены значения улов рассеивания напряжений песка среднего в виде возрастающего вариационного ряда.

113

Таблица 3.3. Вариационный ряд измеренных значений угла рассеивания

напряжений песка среднего

Частное значение угла рас-	Количество	совпадений	Частота	Накопленная
сеивания напряжений	измеренных значений п		f = п / п	частота
30,98		1	0,005	0,005
31,40		2	0,01	0,015
32,02		3	0,015	0,03
32,43		4	0,02	0,05
32,9		5	0,025	0,075
33,41		7	0,035	0,11
33,8		9	0,045	0,155
34,30		11	0,055	0,21
34,83		13	0,065	0,275
35,3		15	0,075	0,35
35,9		17	0,085	0,435
36,27		20	0,1	0,535
36,74		17	0,085	0,62
37,19		15	0,075	0,695
37,73		13	0,065	0,76
38,1		11	0,055	0,815
38,68		9	0,045	0,86
39,1		7	0,035	0,895
39,65		6	0,03	0,925
40,05		5	0,025	0,95
40,55		4	0,02	0,97
41,04		3	0,015	0,985
41,53		2	0,01	0,995
42,01		1	0,005	1

Представленные в табл. 3.3 значения углов рассеивания напряжений могут содержать грубые ошибки, которые необходимо исключить (отсеять) [15, 33, 51]. Для отсева ошибок применяются различные методы. В нормативных документах по статистической обработке экспериментальных данных приводятся методы, которые позволяют отсеивать грубые ошибки из выборок с малым количеством элементов. Например, метод ГОСТ 20522-2012 [15] позволяет отсеивать ошибки из выборок, содержащих до 50 элементов. Представленная выборка содержит 200 элементов и требует применения несколько иных методов отсеивания ошибок, представленных в литературе по обработке экспериментальных данных [33, 51]. Характерной особенностью известных методов отсеивания грубых ошибок является использование распределения Стьюдента. Поэтому используем правило сигм, а также метод, основанный на использовании таблиц распределения Стьюдента [33, 51] для отсева грубых ошибок из больших выборок. В

114

соответствии с правилом сигм определяется интервал, в который попадает случайная величина с соответствующей вероятностью. Границы интервала определяются относительно выборочного среднего значения, от которого откладываются нижняя и верхняя границы. Границы интервала назначаются кратными выборочному среднеквадратическому отклонению. В табл. 3.4 представлены формулы для расчета интервалов и вероятности попадания в них случайной величины [33, 51].

Таблица 3.4. Определение интервала по правилу сигм и вероятность

попадания случайной величины в интервал

Правило сигм для определения величины интер-		Вероятность попадания слу-
	вала	чайной величины в интервал
Границы интервала	гр ср	0,682
Границы интервала	гр ср 2	0,954
Границы интервала	гр ср 3	0,997

Примечание. (ср) – среднеарифметическое значение угла рассеивания напряжений по выборке экспериментальных данных, град; – среднеквадратическое отклонение, град.

Обычно используют правило трех сигм, в соответствии с которым предполагается, что если случайная величина распределена нормально, то ее выход за трехсигмовые пределы практически невозможен, так как вероятность такого события мала и составляет 1-0,997=0,003 [33]. Так как варьирование случайной величины ограничивается трехсигмовыми пределами, то предполагается, что и случайные ошибки ограничены этим интервалом [51]. Тогда можно предположить, что за пределы трехсигмового интервала выходят только грубые ошибки.

В табл. 3.5 приведены результаты проверки выборки по правилу сигм.

Таблица 3.5. Результаты проверки выборки на попадание в трехсигмовый

и двухсигмовый интервалы

Номер про-	n	ср		Нижняя	Верхняя	Значение
цедуры	n	ср		граница	граница	выброса
цедуры				граница	граница	выброса
1	2	3	4	5	6	7
1	200	36,399	2,24	29,679	43,119	Ошибок нет
		Правило двух сигм
1	200	36,399	2,24	31,919	40,879	42,01
2	199	36,371	2,21	31,951	40,971	30,98

115

Окончание табл. 3.5

1	2	3	4	5	6	7
3	198	36,398	2,18	32,038	40,758	41,53
4	196	36,346	2,13	32,086	40,606	31,4
5	194	36,397	2,08	32,237	40,557	41,04
6	191	36,324	2,01	32,304	40,344	32,02
7	188	36,392	1,95	32,492	40,292	40,55
8	184	36,3	1,87	32,56	40,04	32,43
9	180	36,388	1,80	32,788	39,988	40,05
10	175	36,283	1,72	32,843	39,723	Ошибок нет

Из анализа табл. 3.5 следует, что в трехсигмовый интервал попадают все выборочные данные, а в двухсигмовый интервал попадают 180 значений, что составляет 90 %. Таким образом, вероятность попадания в двухсигмовый интервал составила 0,9, что меньше теоретического значения 0,954, соответствующего 191 значению. В данном случае от оценки по двухсигмовому интервалу следует воздержаться.

Рассуждения автора построены на том, что если выборочные данные близки к нормальному закону распределения, то отсев 20 (10 %) результатов приведет к исключению не только грубых, но и случайных ошибок. В этом случае изменится частота значений вариационного ряда, а закон распределения исказится. С другой стороны, результаты табл. 3.13 интересны для анализа при дальнейшей проверке выборки. Из этой таблицы следует, что при доверительной вероятности 99,1 % среди отсеянных значений грубых ошибок быть не должно, а при – 95,4 % должны иметь место выбросы, которые могут являться как грубыми, так и случайными ошибками.

Если предположить, что равенство между максимальной абсолютной величиной отклонения случайной величины от среднего значения выборки и границы интервала имеет место при определенном значении постоянного множителя t при среднеквадратическом отклонении, то величину этого множителя можно найти по одной из формул

t ср min ;

t max ср ,

(3.3)

где (min) и (max) – наименьшее и наибольшее значения угла рассеивания напряжений в вариационном ряде, попавшие в трехсигмовый интервал о.

Так как в рассматриваемом случае наибольшее отклонение имеет значение 42,01, то

t 42,01 36,399 2,505.

116

Используя таблицу функции интегральной вероятности, найдем Ф=0,9938, тогда Ф0=0,9938-0,5=0,4938, а вероятность попадания случайной величины в интервал (гр)= (ср) 2,505 составит F=2 0,4938=0,9876. В том случае если данные предположения верны, то при уровне значимости р 1,24 % выбросов за пределы указанного интервала быть не должно.

Для проверки выборки используем метод, рекомендованный Л.З. Румшиским [51]. Этот метод аналогичен методу, регламентируемому ГОСТ 20522-2012, но с критическими значениями для выборок, содержащими элементы в количестве более 50. Критические значения приведены для п=100 и п= , между которыми допускается интерполяция. Процедура этого метода проверки выборочных данных приведена в табл. 3.6.

Таблица 3.6. Последовательность проверки выборки с использованием

метода [51]

Шаг

Действие словами

Формула

ср

Расчет среднеарифметического зна-

где п – количество совпадений

чения угла рассеивания напряжений

измеренных значений (частота) уг-

в выборке

лов рассеивания напряжений ; п –

общее количество значений изме-

рений (сумма всех п )

Расчет среднеквадратического от-

n ср 2

клонения

n 1

Выделяют наблюдение с наиболь-

max

ср

шим по модулю отклонением

Рассчитывают характеристику для

max

ср

выделения аномального значения

При заданной надежности и числе

Интерполяция табличных данных

определений рассчитывают крити-

источника [21]

ческие значения tn

Проверка условия выбраковывания

результатов

В том случае если на шаге 6 условие выполнено, то значение отбрасывается, а для оставшихся элементов выборки вся процедура повторяется.

Аналогичный метод проверки выборочных данных на наличие аномальных значений рекомендован Е.Н. Львовским [33]. В этом ме-

117

тоде оцениваемый параметр определяется так же, как и в табл. 3.6. То есть первые четыре шага в обоих методах одинаковые. Отличие состоит в том, что критические значения вычисляются с помощью процентных точек распределения Стьюдента. Процедура этого представлена в табл. 3.7.

Таблица 3.7. Последовательность метода отсева грубых ошибок при

расчете критических значений с помощью процентных точек распределения Стьюдента

Шаг	Действие словами			Формула
1	2	3
1	Расчет среднеарифметического значения угла	Так же, как в табл. 3.6
1	рассеивания напряжений в выборке	Так же, как в табл. 3.6
2	Расчет среднеквадратического отклонения	Так же, как в табл. 3.6
3	Выделяют наблюдение с наибольшим по моду-	Так же, как в табл. 3.6
	лю отклонением
4	Рассчитывают характеристику для выделения	Так же, как в табл. 3.6
4	аномального значения	Так же, как в табл. 3.6
	Определение процентных точек распределения	Интерполяция таблич-
5	Стьюдента [p, n-2] при числе степеней свободы	ных данных источника
	п-2 и заданных р	[33]
				р,п 2
6				р,п 2	п 1
6		р
	Расчет критического значения р			п 2 р,п 2 2
				п 2 р,п 2 2
	При соблюдении условия отсев не делают			p1
	Отсев можно выполнить, если в пользу проце-
7	дуры имеются и другие соображения. В против-		p1 p2
7	ном случае от исключения ошибок рекоменду-		p1 p2
	ном случае от исключения ошибок рекоменду-
	ется воздержаться
	Отсев выполняют всегда			p2

Примечание. р1 и р2 – критические значения, рассчитанные в шаге 6 с использованием процентных точек распределения Стьюдента [p, n-2] для р1=5% и

р2=0,1%.

В том случае если на шаге 7 значение превышает максимальное критическое значение, то частное значение угла рассеивания напряжения исключается из выборки, а для оставшихся в выборке элементов вся процедура повторяется заново. Процентные точки распределения Стьюдента принимают при р, изменяющемся в диапазоне от 0,1 до 5 %. В табл. 3.8 и 3.9 приведены результаты проверки выборки с углов рассеивания напряжений в песке среднем на наличие грубых ошибок по методам, представленным в табл. 3.6 и 3.7.

118

Таблица 3.8. Результаты проверки выборки по методу табл. 3.6

Номер	n	ср			Надежность	Критическое значе-
процедуры	n	ср			Надежность	ние
процедуры						ние
					0,95	1,977
1	200	36,39	2,24	2,51	0,98	2,332
1	200	36,39	2,24	2,51	0,99	2,607
					0,99	2,607
					0,999	3,35

Из анализа данных табл. 3.8 следует, что р 2% значение из выборки выпадает, а при р 1 % в выборке грубых ошибок нет. Это практически подтверждает ранее сделанный нами вывод о попадании случайной величины в интервал (гр)= (ср) 2,505 с вероятностью F=0,9876. В этом случае от выбраковки результатов следует воздержаться.

Таблица 3.9. Результаты проверки выборки по методу с использованием

процентных точек распределения Стьюдента (метод табл. 3.7)

Номер	n	ср			р, %		р	Исключенное
процедуры								значение
						[p, n-2]
1	200	36,39	2,24	2,51	0,1	3,1321	3,065	Ошибок нет
					5	1,6524	1,6453

Таким образом, все методы показали, что грубых ошибок выборка не содержит. В связи с чем для последующей обработки принимаем выборку, представленную вариационным рядом табл. 3.3.

Обработку экспериментальных данных выполняют по вариационному и статистическому рядам. В статистическом ряде экспериментальные данные группируются в разряды [1, 8]. Эмпирическую функцию распределения непрерывной случайной величины задают аналитически в виде математического выражения или графически в виде ломаной линии или гистограммы. По оси абсцисс откладывают частотные интервалы, охватывающие все возможные варианты, а по оси ординат откладывают накопленную частоту попадания случайной величины в частотные интервалы [8, 10, 25]. Закон распределения задается следующим образом. Вначале определяется статистический интервал, в пределах которого варьируется измеренная случайная величина. Длина статистического интервала определяется разностью максимального и минимального значений. Затем подбирается количество разрядов, на которые разбивается этот интервал. При объеме выборки до 100 элементов (параметров) минимальное количество разрядов

119

принимают 6 – 7, а если объем выборки составляет несколько сотен элементов, то количество интервалов назначают 10–20. Количество интервалов можно рассчитать по правилу Штюргеса, которое приводится в работах различных авторов [33]. Далее отношением длины интервала к количеству разрядов определяется размер разряда статистического интервала [33]. Для расчета длины интервала и разрядов рекомендуются простые формулы, представленные в табл. 3.10.

Таблица 3.10. Формулы для расчета длины интервалов и разрядов [33]

Характеристика		Формула для расчета
Длина статистического ин-		Lx xmax xmin,
тервала (размах варьирова-	где хmax и хmin – максимальное и минимальное из-
ния) Lх	меренные значения характеристики
Ориентировочное количест-	nx 1 1,441 lnn 1 3,32 lgn,
во разрядов nx	где n – число измеренных характеристик х или
	число определений

Длина разряда lx	lx	xmax xmin	xmax xmin
			1 1,441 lnn
		nx

При количестве частных значений угла рассеивания напряжений 200 количество разрядов принято 9. Максимальное и минимальное значения угла рассеивания напряжений песка среднего составили 42,01 и 30,98о. Отсюда длина интервала 11,03о, а длина разряда

1,2256о.

В табл. 3.11 приведены экспериментальные данные углов рассеивания напряжений в песке среднем, сгруппированные по разрядам.

Таблица3.11.Экспериментальные данные, сгруппированные по разрядам

Номер	Границы интер-		Число по-	Частота					Накопленная		n i
Номер	вала		паданий в			n		i	частота	f	n i
интер-			интервал	n					m	f	l
вала i			интервал	i			n		m		l
вала i							n		n n
	min	max	ni						i
			ni						i 1
1	30,98	32,2056	6		0,03				0,03	0,02448
2	32,2056	33,4311	16		0,08				0,11	0,06527
3	33,4311	34,6567	20		0,1				0,21	0,08159
4	34,6567	35,8822	28		0,14				0,35	0,11423
5	35,8822	37,1078	54		0,27				0,62	0,2203
6	37,1078	38,3333	39		0,195				0,815	0,15911
7	38,3333	39,5589	16		0,08				0,895	0,06527
8	39,5589	40,7844	15		0,075				0,97	0,06119
9	40,7844	42,01	6		0,03				1	0,02448

120

Значение параметров, вычисленных по ограниченному объему экспериментальных данных, может изменяться от выборки к выборке. Поэтому при обработке данных необходимо получить статистическую оценку параметра распределения [33, 51]. В табл. 3.12 приведены формулы для определения параметров теоретических распределений математического ожидания, дисперсии и зависящего от нее среднеквадратического отклонения. Эти параметры используют для сравнения с первым и вторым моментами эмпирического распределения, а также даны формулы для расчета среднеквадратического отклонения.

Таблица 3.12. Формулы для расчета математического ожидания,

дисперсии и среднеквадратического отклонения некоторых теоретических распределений [1, 44, 57]

Параметр распределе-

Формула для оценки параметра

ния

1 2

Равномерное распределение

Математическое

ожи-

a b

дание

Дисперсия

средне-

b a 2

b a

квадратическое

откло-

;

2 3

нение

Нормальное распределение

Математическое

ожи-

дание

i 1

Дисперсия

средне-

квадратическое

откло-

D 2

Mx 2

;

x Mx 2

нение

n 1 i 1

n 1

i 1

Логарифмическое нормальное распределение

Математическое

ожи-

дание

ln xi

i 1

D 2

lnx Mx 2 ;

Дисперсия

средне-

n 1

i 1

квадратическое

откло-

нение

lnxi Mx 2

n 1

i 1

Распределение Максвелла

Математическое

ожи-

дание

i 1

Дисперсия

средне-

0,454 a

;

квадратическое

откло-

нение

121

Продолжение табл.3.12

Экспоненциальное распределение

Математическое ожидание

Дисперсия и среднеквад-

ратическое отклонение

;

Гамма-распределение

Математическое ожидание

i 1

Дисперсия и среднеквад-

D 2

2 ;

ратическое отклонение

Распределение Эрланга

Математическое ожидание

Дисперсия и среднеквад-

;

ратическое отклонение

Распределение Эрланга нормированное

Математическое ожидание

Дисперсия и среднеквад-

D 2

;

ратическое отклонение

k a2

Гиперэкспоненциальное распределение

n q

Математическое ожидание

i 1ai

;

Дисперсия и среднеквад-

i 1ai2

i 1ai

ратическое отклонение

i 1a

i 1ai

Распределение Парето

Математическое ожидание

k a

k 1

Дисперсия и среднеквад-

D 2

;

k 1 2

k 2

ратическое отклонение

k 2

k 1

Распределение Лапласа

Математическое ожидание

Mx a

Дисперсия и среднеквад-

;

ратическое отклонение

122

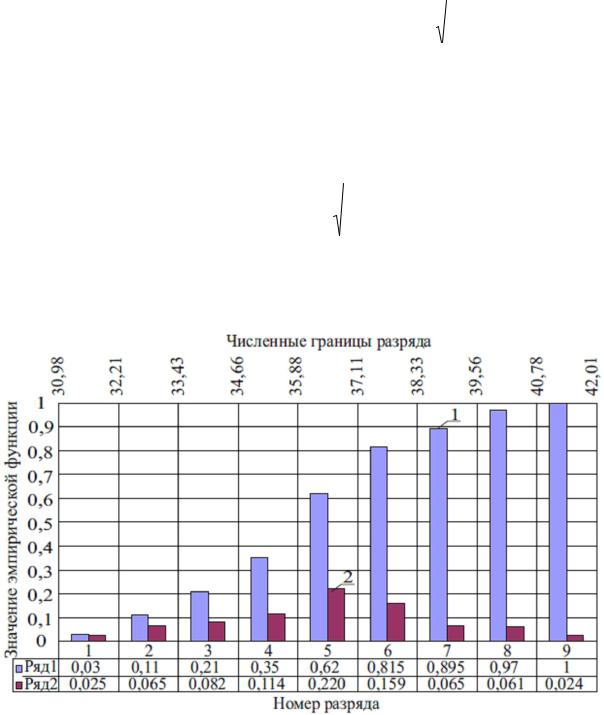
Окончание табл. 3.12

Распределение Уи́ льяма Си́ ли Го (Стьюдента)

Математическое

ожи-

Mx 0

, при n>1

дание

Дисперсия

средне-

квадратическое

откло-

;

n 2

нение

n 2

Распределение Вейбулла двухпараметрическое

Математическое

ожи-

Mx Г 1

дание

Г 1

;

Дисперсия

средне-

квадратическое

откло-

нение

Г 1

На рис. 3.23 приведены эмпирические функции распределения и вероятности распределения угла рассеивания напряжений.

Рис. 3.23. Эмпирические функции распределения и плотности вероятности по разрядам угла рассеивания напряжений в песке среднем: 1 – эмпирическое распределение вероятности F = п I; 2 – эмпирическая плотности вероятности (частотность) f

123

Из анализа этого рисунка следует целесообразность принятия нулевой гипотезы о нормальном распределении случайной величины.

Приблизительную проверку нормальности распределения можно произвести по методу, предложенному Лотером Заксом [18]. Суть этого метода заключается в сравнении отношения размаха варьирования к среднеквадратическому отклонению с критическими границами этой характеристики при принятом уровне значимости [18]. В табл. 3.13 приведены результаты расчета статистик по этому методу. Из табл. 3.13 следует, что оцениваемый параметр больше нижней границы и меньше верхней границы, а это значит, что гипотеза о нормальности распределения подтверждается с уровнем значимости 0,1.

Таблица 3.13. Результаты расчета статистик и проверки нормальности

распределения по методу Лотера Закса [18]

Характеристика	Формула для расчета			Величина
Характеристика	Формула для расчета			характеристики
Размах варьирования	L max min			11,03

		1	n
Среднеквадратическое отклонение		1	i ср 2	2,24
Среднеквадратическое отклонение		n 1	i ср 2	2,24
		n 1	i 1
Оцениваемый параметр		R L		4,92
Критические значения при объеме	Принимается по табли-			4,90
выборки 200 и уровне значимости	це нижних и верхних
выборки 200 и уровне значимости	це нижних и верхних			6,15
0,1		границ [18]		6,15

Используя таблицу критических значений [18], несложно убедиться, что гипотеза нормальности распределения принимается при любом уровне значимости от 0 до 10 %. Как известно, уровень значимости представляет собой вероятность возникновения ошибки первого рода при проверке нулевой гипотезы. В технике уровень значимости обычно принимается 0,02 – 0,1. Однако согласно рекомендациям [33] для метода Закса важным является подтверждение гипотезы с уровнем значимости 0,1, что и выполнено в табл. 3.13.

Другую приблизительную проверку дает оценка выборочного значения коэффициента вариации, представляющего собой отношение выборочного среднеквадратического отношения к среднему арифметическому. Коэффициент вариации рассматриваемой выборки составляет 6,15 %. В соответствии с ГОСТ 20522-2012 коэффициент вариации характеристики при обработке экспериментальных данных с использованием нормального закона распределения не должен пре-

124

вышать 30 %, а по статистической литературе [33] 33 %. Так как вычисленное значение коэффициента вариации меньше 33 %, то есть еще одно основание принимать гипотезу нормальности распределения.

Методы подбора теоретического распределения основаны на оценках эмпирического распределения [32]. Одним из таких методов является метод моментов [39]. При использовании этого метода определяют начальные и центральные моменты по выборке и сгруппированным данным. Вначале определяют смещенные оценки моментов, а потом переходят к несмещенным оценкам [39]. Принятые оценки моментов эмпирического распределения сравнивают с оценками теоретического распределения. Число сравниваемых оценок моментов принимается по количеству параметров в теоретической функции распределения. То есть для сравнения с двухпараметрическими теоретическими функциями используют первые две оценки моментов, а для сравнения с трехпараметрическими – три оценки моментов. Однако определение параметров асимметрии и эксцесса, на основе которых можно получить приблизительные представления о близости или отличии эмпирического к нормальному закону, требует использования третьего и четвертого моментов.

Отметим, что метод моментов позволяет получить эффективные оценки только для нормального распределения, а для других распределений эффективность метода моментов невысокая [39]. Поэтому в первую очередь проверяют гипотезу о нормальном распределении экспериментальных данных, что и требуется установить для рассматриваемой выборки. Формулы для определения оценок моментов даны в табл. 3.14, а их значения – в табл. 3.15.

Таблица 3.14. Формулы для расчета оценок моментов [39]

Оценка моментов	Формула для расчета оценки моментов
1			2
	M		1		n		,
Смещенный краевой		1				i

момент первого по-				n i 1
рядка	где i и n – порядковый номер и общее количество изме-
	ренных углов рассеивания напряжений

Смещенные оценки		1	n
центральных момен-	Mk				i M1 k

		n
тов порядка k по ва-			i 1
риационному ряду

125

Окончание табл. 3.14

Мнс1

i М1 ; Мнс2

i М1 2 ;

Несмещенные оценки

п 1i 1

центральных момен-

п М3

3 ;

нс3

тов по вариационному

п 1 п 2

i 1

ряду

Мнс4

2 n 3 М4 3 n 2 n 3 М2

п 1 п 2 п 3

M1р

nv цv ,

Оценки моментов по

v 1

где v и V – номер и количество интервалов (разрядов);

сгруппированным в

цv – значение угла рассеивания напряжений в центре

разряды эксперимен-

тальным данным

v-го интервала.

M1р

nv цv M1р k

v 1

Таблица 3.15. Оценки моментов, вычисленные по вариационному ряду

и по разрядам эмпирического распределения

Оценки моментов		Порядок оценки момента
Оценки моментов	1	2	3	4
	1	2	3	4
Смещенные моменты по ва-	36,399	4,997	0,879	67,559
риационному ряду	(-1,6 10-15)	4,997	0,879	67,559
Несмещенные моменты по ва-	36,582	5,02	0,884	67,898
риационному ряду	(-1,6 10-15)	5,02	0,884	67,898
Оценки моментов по сгруппи-	36,495
рованным в разряды экспери-	(-5 10-12)	5,122	-0,442	70,228
ментальным данным

Примечание. Во втором столбце без скобок даны значения первого краевого момента, а в скобках приведены значения первого центрального момента.

Первый центральный момент эмпирического распределения приблизительно равен нулю, что справедливо для теоретического нормального распределения.

Приблизительные представления о близости эмпирического распределения к нормальному закону, но без установления нормальности распределения дает анализ показателей асимметрии и эксцесса [33], для вычисления которых используются второй, третий и четвертый моменты.

В табл. 3.16 приведены формулы и результаты расчета показателей асимметрии и эксцесса.

126

Таблица 3.16. Формулы и результаты расчета показателей асимметрии

и эксцесса эмпирического распределения углов рассеивания напряжений в песке среднем

Характеристика	Формула					Величина
Показатель асимметрии	g1		М3			0,079

				М	3
				М	3
					2
Показатель эксцесса	g2	М4			3	-0,31
Показатель эксцесса	g2	М22			3	-0,31
		М22

Для симметричных распределений g1=0, а для нормального распределения g2=0. Таким образом, из табл. 3.16 следует, что эмпирическое распределение имеет некоторую асимметрию и определенный эксцесс по сравнению с теоретическим нормальным распределением. Так как показатель асимметрии эмпирического распределения имеет положительное значение, то правая часть графика длиннее левой. Показатель эксцесса имеет отрицательное значение, что позволяет сделать вывод о том, что пик эмпирического графика вероятности распределения более низкий и пологий по сравнению с теоретическим нормальным распределением.

Проверку гипотезы нормальности распределения можно выполнить по несмещенным оценкам показателей асимметрии и эксцесса [33]. Для этого несмещенные оценки сравнивают со среднеквадратическими отклонениями показателей эксцесса и асимметрии. В табл. 3.17 приведены критерии и формулы для вычисления несмещенных оценок и их среднеквадратических отклонений.

Таблица 3.17. Критерии нормальности распределения и формулы

расчета

несмещенных оценок

и среднеквадратических отклонений

показателей асимметрии и эксцесса

Статистика

Формула

Несмещенные оценки показате-

n 1 n 1 g2 6

n n 1

лей асимметрии G1 и эксцесса

g1; G2

n 2

n 2 n 3

6 n n 1

Среднеквадратическое

отклоне-

;

n 2 n 1 n 3

ние показателей асимметрии и

24 n n 1 2

эксцесса

n 3 n 2 n 3 n 5

Критерии

принятия

гипотезы

3 G1;

5 G2

нормального распределения

127

В табл. 318 даны результаты вычислений оценок и среднеквадратических отклонений показателей асимметрии и эксцесса.

Таблица 3.18. Результаты расчета оценок и среднеквадратических

отклонений показателей асимметрии и эксцесса

Характеристика			Величина
Несмещенная оценка показателя асимметрии \|G1 \|			0,08
Среднеквадратическое	отклонение показателя асимметрии		0,172
G1

Критическое значение	среднеквадратического	отклонения	0,516
показателя асимметрии 3 G1

Несмещенная оценка показателя эксцесса \|G2 \|			0,283
Среднеквадратическое отклонение показателя эксцесса G1			0,342
Критическое значение	среднеквадратического	отклонения	1,71
показателя эксцесса 5 G2

Из данных табл. 3.18 следует, что условия табл. 3.17 выполняются, следовательно, гипотезу о нормальности распределения можно принять.

Для проверки гипотезы нормальности распределения достаточно широко применяется критерий согласия Пирсона 2 (хи-квадрат). В соответствии с этим методом вычисляют значение 2, которое сравнивается с табличным значением. В том случае если вычисленное значение меньше табличного, то гипотеза нормальности распределения принимается. Вычисление статистик производят по сгруппированным в разряды данным. В табл. 3.19 и 3.20 представлены результаты вычисления статистики 2.

Таблица 3.19. Подготовка данных для вычисления статистики 2

(вспомогательная таблица)

Номер	Середи-	Час-					z	i
Номер	Середи-	Час-		M1	i	Мнс2		i
разря-	на раз-	тоты	f i	M1	i	Мнс2
да	ряда i	f
1	31,593	6	189,56		-4,9022		-2,16624
2	32,818	16	525,09		-3,6767		-1,6247
3	34,044	20	680,88		-2,4511		-1,08312
4	35,269	28	987,54	36,495	-1,2256	2,263	-0,54158
5	36,495	54	1970,7	36,495	0	2,263	0
6	37,721	39	1471,1		1,2256		0,541582
7	38,946	16	623,14		2,4511		1,08312
8	40,172	15	602,58		3,6767		1,624702
9	41,397	6	248,38		4,9022		2,16624
Итого	–	200	7299	–	–	–		–

128

Таблица 3.20. Результаты расчета статистики 2
	Плотность вероятности						Величина			Величина
№	нормального распределения						k fст			f −k f
№											ст
раз-	по формуле					по
ряда		ехр 0,5 z			2	по	fст по	fст по		fст по	fст по
ряда						таблице
						таблице
	fст			2		[33]	расчету	таблице		расчету	таблице
				2		[33]
1		0,038198				0,0379	4,1374	4,10519		1,86257	1,89481
2		0,106617				0,1074	11,5487	11,63318		4,45164	4,36682
3		0,22196				0,2227	24,0419	24,12206	-4,0419		-4,12206
4		0,34461				0,3448	37,327	37,34749		-9,327	-9,34749
5		0,399043				0,3989	43,223	43,20741		10,7771	10,79259
6		0,34461				0,3448	37,327	37,34749		1,67303	1,65251
7		0,22196				0,2227	24,0419 24,12206 -8,0419 -8,12206
8		0,106617				0,1074	11,5484	11,63318		3,45164	3,36682
9		0,038198				0,0379	4,1374	4,10519		1,86257	1,89481
				k l n						108,3164
Статистика			2	f	k fст 2		При расчете fст			12,89
	2				k	fст	При взятии fст по таб-			12,91
					k	fст	лице			12,91
Примечание. Теоретические плотности нормального распределения (теоретиче-
ские частоты) определены двумя способами, вычислены по формуле и взяты по
таблице [33].

В табл. 3.21 приведены критические значения статистики 2.

Таблица 3.21.	Критические значения статистики 2
Число степе-	Доверительная вероятность F и уровень значимости р
ней свободы	0,80	0,90	95	0,975	0,98	0,99	0,995	0,999
nх-1-2	0,20	0,10	0,05	0,025	0,02	0,01	0,005	0,001
9-1-2=6	8,558	10,65	12,59	14,45	15,03	16,81	18,55	22,46

Табличное критическое значение составляет 14,449 при уровне значимости 2,5 %. Так как вычисленное значение 2 меньше этого табличного критического значения, то гипотезу о нормальном распределении можно принять на уровне значимости 2,5 %.

На основе критерия 2 разработан ряд критериев согласия, например в виде статистик В.И. Романовского или Б.С. Ястремского

[33, 51].

В табл. 3.22 приведены статистики В.И. Романовского и Б.С. Ястремского и результаты проверки этих критериев согласия.

129

Таблица 3.22. Результаты расчета статистик и проверки критериев

согласия В.И. Романовского и Б.С. Ястремского

Статистика В.И. Романовского									Статистика Б.С. Ястремского
	2		К	12,91		6		КР			2	п	12,91 9

КР							2							0,87
					2 6
		2 К								2 п 4			2 9 4 0,6

Критерий согласия В.И. Романовского	Критерий согласия Ястремского
2 3	0,87 3

Из анализа табл. 3.22 следует, что гипотезу о нормальном распределении можно принять.

Из всех рассмотренных выше статистических критериев Лотара Закса, выборочного коэффициента вариации, несмещенных оценок показателей асимметрии и эксцесса, Пирсона, В.И. Романовского и Б.С. Ястремского критерии согласия с вычислением статистики 2 считаются наиболее основательными. Поэтому для доверительной оценки истинного значения примем уровень значимости 2 % и соответствующую этому значению доверительную вероятность 98 %. Доверительная оценка истинного значения определяется по формуле

t	3		,	(3.4)

		п

где t – коэффициент, принимаемый по таблице распределения Стьюдента в зависимости от числа степеней свободы (к=п-1) и двусторонней доверительной вероятности.

При доверительной вероятности параметр распределения Стьюдента при 199 степенях свободы составит 2,345. Тогда доверительная оценка истинного значения составит 1,115 о. Отсюда, откладывая доверительную оценку от несмещенного математического ожидания 35,582, получим, что интервал варьирования истинного значения угла рассеивания напряжения в песке среднем составит от 34,5 до 36,7 о.

Лабораторные испытания и обработка результатов проведены совместно с Н.П. Александровой, Н.В. Кузиным и Г.В. Долгих3.

На втором этапе лабораторных исследований производилось сопоставление угла рассеивания напряжений с углом внутреннего трения песка. Цель таких экспериментов заключалась в оценке возможности применениякрасчетунапряженийформул (2.59), (2.60)или (2.63)и (2.64).

3 Исследование вертикальных напряжений в земляном полотне с учетом распределяющей способности грунтов / А.С. Александров и др. // Транспортное строительство. – 2010. – №8. – С. 18 – 21.

130

Угол внутреннего трения определил В.А. Гриценко при помощи прибора прямого среза (рис. 3.24) испытанием образцов (рис. 3.25), изготовленных при помощи прибора стандартного уплотнения.

Рис. 3.24. Определение угла внутренне-	Рис. 3.25. Образцы песка для испыта-
го трения в приборе прямого среза	ний на срез

Рис. 3.26. Общий вид образца песка	Рис. 3.27. Извлечение колец из песча-
среднего с запрессованными кольцами	ного образца

Уплотнение песка производилось при его оптимальной влажности в три слоя при 40 ударах по каждому слою, то есть в соответствии с общепринятой методикой (рис. 3.26). Отличие состояло в том, что внутри цилиндрической формы размещались кольца прибора прямого

131

среза, которые после изготовления большого цилиндрического образцы аккуратно изымались (рис. 3.27).

Три образца испытывались на приборе прямого среза. Вариация количества ударов при изготовлении образцов позволила определить зависимость угла внутреннего трения от плотности песка. После выполнения всех испытаний произведено сопоставление углов рассеивания напряжений и углов внутреннего трения .

Результаты такого сопоставления для песка средней крупности приведены в табл. 3.23.

Таблица 3.23. Сопоставление экспериментальных значений

математического ожидания угла рассеивания напряжений и угла внутреннего трения песка среднего

Разновидность	Математическое ожида-	Угол внутреннего	Расхождение
песка	ние угла рассеивания	трения		, %
	напряжений
Мелкий	32,3	35,6	9,3
Средний	35,6	37,4	4,8

Из анализа данных табл. 3.23 следует, что математическое ожидание угла рассеивания напряжений вертикального сжатия отличается от угла внутреннего трения приблизительно на 5 % для песка среднего и 10 % для песка мелкого. Поэтому для песка среднего можно принять =0,95 и =0,95 , а для песка мелкого – =0,90 и =0,9 .

Аналогичные испытания и статистическая обработка их результатов выполнены с глинистыми грунтами. Подробные вычисления приведены в квалификационной работе Г.В. Долгих [17], выполненной под научным руководством автора. Г.В. Долгих установил, что несмещенное математическое ожидание угла рассеивания напряжений в суглинке легком при оптимальной влажности и коэффициенте уплотнения, равном единице, составляет 25,26 о. Доверительная оценка истинного значения составила 1,08 о, а истинное значение угла рассеивания напряжения в суглинке легком варьируется в 24,2 – 26,2 о.

Анализируя данные, полученные Г.В. Долгих, отметим, что в интервал варьирования угла рассеивания напряжений суглинка легкого попадает значение 26 о, которое авторы работ [74, 82, 83] рекомендуют принимать при расчете сопротивления недренированному сдвигу.

Отсюда следует, что при оптимальной влажности и максимальной стандартной плотности суглинка величина составляет 24 – 26о.

132

Выводы по главе 3

Из анализа материалов, изложенных в данной главе, можно сделать следующие выводы:

1.Разработан способ экспериментальной оценки распределяющей способности грунта, позволяющий вычислять угол рассеивания нормального вертикального напряжения непосредственно из данных эксперимента.

2.Выполненные испытания песчаных и глинистых грунтов показали, что разновидности этих грунтов (песок средний, песок мелкий и суглинок легкий) обладают распределяющей способностью, а величина угла рассеивания напряжений зависит от разновидности грунта. Значит угол рассеивания напряжения является параметром материала.

3.Для песков мелких и средней крупности математическое ожидание угла рассеивания напряжений от величины угла внутреннего трения отличается приблизительно на 5 и 10 %. Поэтому при расчете главных напряжений по формулам (2.63) и (2.64) целесообразно принимать:

–песка среднего =0,95, а =0,95 ;

–песка среднего =0,90, а =0,90 .

4. Дальнейшие экспериментальные исследования могут быть выполнены при различных показателях физических свойств грунтов, к которым прежде всего относятся плотность сухого грунта и влажность.

133

4. РАСЧЕТ ДОРОЖНЫХ КОНСТРУКЦИЙ ПО СОПРОТИВЛЕНИЮ СДВИГУ

Расчет дорожной конструкции по сопротивлению сдвигу дискретных материалов и грунтов земляного полотна обеспечивает отсутствие нарушения целостности конструктивного элемента по линии скольжения и снижение необратимых деформаций, накапливаемых материалом или грунтом. Причем в том случае если обеспечивается работа материала или грунта в стадии уплотнения, то пластические деформации сдвига отсутствуют. В стадии уплотнения остаточная деформация обусловлена уменьшением объема материала или грунта, которому сопутствует уменьшение пористости. При воздействии повторной нагрузки деформации уплотнения уменьшаются с возрастанием числа приложенных нагрузок и в конечном итоге исчезают полностью. Дальнейшее деформирование протекает только за счет обратимых деформаций. По величине давления стадия уплотнения ограничивается первой критической нагрузкой Н.М. Герсеванова, которую для дискретных материалов и грунтов в условиях воздействия повторных нагрузок можно считать пределом пластической приспособляемости. Поэтому обеспечение работы дискретных материалов и грунтов в стадии уплотнения является важным элементом проектирования дорожной конструкции. Сложность решения этой задачи состоит в том, что подстановка в одно и то же условие пластичности различных формул, предназначенных для расчета главных напряжений, приводит к разным значениям касательных напряжений по этому условию пластичности. При вариации угла Лоде практически во всем диапазоне различные условия пластичности при подстановке в них одних и тех же формул расчета главных напряжений дают разные значения касательных напряжений. Таким образом, известные условия пластичности и предложенные нами модифицированные модели расчета главных напряжений дают большое количество сочетаний «условие пластичности–модифицированная модель расчета главных напряжений». Каждое такое сочетание приводит к индивидуальным, то есть характерным только для данного сочетания, значениям касательных напряжений. Поэтому необходимо выполнить достаточно большой объем теоретических исследований, в результате которых будут созданы такие сочетания, по каждому из которых необходимо вычислить касательные напряжения. Сопоставлением с данными опыта необходимо определить наиболее пригодные сочетания.

134

4.1. Критерий оценки сопротивления сдвигу и обоснование расчетной схемы при проектировании дорожной конструкции

Проверка дорожной конструкции по условию сопротивления сдвигу является одним из трех обязательных критериев ее проектирования по прочности. Такой расчет выполняется с момента вступления в действие ВСН 46-72 [19]. По мере совершенствования нормативной базы отдельные элементы этого расчета модифицировались, как правило, за счет уточнения некоторых коэффициентов. Историю модификации метода расчета можно проследить на основе анализа мате-

риалов нормативов ВСН 46-83 [22], ВСН 197-83 [20], ВСН 197-91 [21], ОДН 218.046-01 [46], ОДМ [38]. Современное название данного критерия проектирования «Расчет по условию сдвигоустойчивости подстилающего грунта и малосвязных конструктивных слоев». В этом критерии подстилающим грунтом земляного полотна является поверхность земляного полотна, а малосвязным конструктивным слоем – песчаный дополнительный слой основания дорожной одежды. Предельное состояние по этому критерию расчета записывается в виде равенства активного напряжения сдвигу отношению его предельной величины к коэффициенту прочности [46, 47]. Предельная величина активного напряжения сдвигу определяется произведением сцепления и коэффициентов, учитывающих особенности работы дорожной конструкции. Активное напряжение сдвига находится суммой касательных напряжений от собственного веса дорожной одежды и воздействия транспортной нагрузки. Величина касательных напряжений от транспортной нагрузки определяется левой частью критерия Кулона – Мора, а именно по формуле (2.82). Таким образом, согласно традиционным представлениям специалистов дорожной отрасли в условии пластичности Кулона – Мора сцепление обуславливает прочность материала на сдвиг, а угол внутреннего трения «гасит» величину касательного напряжения. То есть чем больше величина угла внутреннего трения, тем меньше касательное напряжение, вычисленное по

(2.82).

Анализируя структуру нормативного метода расчета [46, 47], отметим, что величина главных напряжений 1 и 3 должна определяться суммой главных напряжений от транспортной нагрузки и собственного веса. Такая схема вычисления касательных напряжений по условию Кулона – Мора применена Н.П. Пузыревским [48] для расчета величины безопасного давления, а впоследствии была развита в

135

работах Н.Н. Маслова [34], И.В. Яропольского [61] и других специалистов [2, 3]. Применение этого способа расчета касательных напряжений в нормативных методах приведет к изменению касательных напряжений, вычисляемых в одних и тех же точках элемента дорожной конструкции.

Любое условие пластичности можно решить относительно величины давления, приложенного к поверхности полупространства или слоя конечной толщины. Поэтому критерий расчета по сопротивлению сдвигу можно записать как в касательных напряжениях, так и в давлениях, воспринимаемых поверхностью рассчитываемого элемента дорожной конструкции. В этом случае критерий сопротивления сдвигу имеет вид

рб	Кпр,	(4.1)

рзп

где рб – безопасное давление, МПа; рзп – давление, передаваемое дорожной одеждой на земляное полотно, МПа; Кпр – коэффициент прочности, принимаемый таким же, как и в нормативных методах расчета по касательным напряжениям.

Под безопасным давлением понимается величина давления, воспринимаемого рассчитываемым элементом дорожной конструкции, при котором в его наиболее опасной точке возникает предельное состояние по условию пластичности, положенному в основу расчета этой характеристики. Таким образом, теоретическая величина безопасного давления зависит от двух факторов:

–условия пластичности, из которого выводится формула для его расчета;

–модифицированной модели, по которой рассчитываются главные напряжения в принятом условии пластичности.

Эти же параметры расчета обуславливают местоположение наиболее опасной точки, в которой возникает наибольшее касательное напряжение по принятому условию пластичности. При использовании любой из предлагаемых модифицированных моделей расчета главных напряжений наиболее опасная точка расположена в сечении по оси симметрии нагрузки на определенном расстоянии от поверхности земляного полотна. Это расстояние и является местоположением наиболее опасной точки.

Нормативный метод проверки условия сопротивления сдвигу предполагает расчет двухслойной системы. Верхний слой такой системы, расположенный над проверяемым элементом дорожной конст-

136

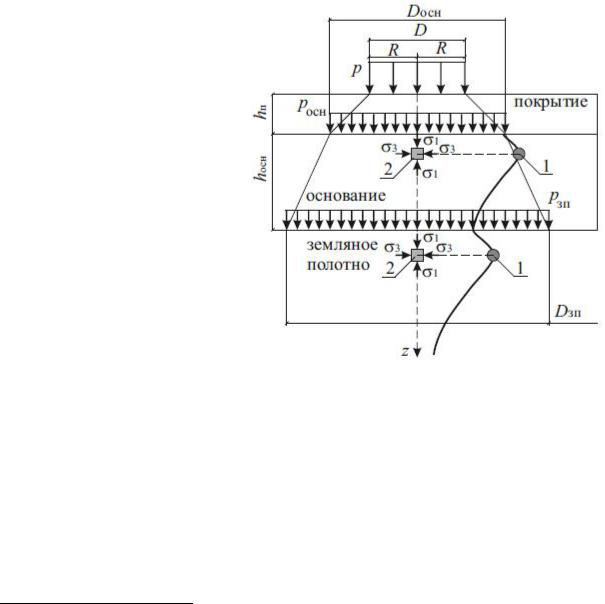
рукции, характеризуется суммарной толщиной всех входящих в него слоев и модулем упругости, вычисленным как усредненное по толщине значение. Нижний слой характеризуется общим модулем упругости на поверхности проверяемого элемента дорожной конструкции. Если для такой двухслойной системы построить эпюру касательных напряжений, то наиболее опасная точка будет находиться в верхнем слое системы. Во всех других точках, расположенных ниже наиболее опасной точки, напряжение по глубине убывает. Вследствие этого считается, что наиболее опасная точка возникает на границе раздела слоев двухслойной системы.


В работе4 автор со-
вместно с Г.В. Долгих и
А.Л. Калининым предло-
жили изменить расчетную
схему	дорожной		конст-
рукции, в соответствии с
которой касательные				на-
пряжения		в проверяемом
элементе		рассчитываются
от давления, приложенно-
го к	поверхности этого
элемента. Сделанное нами
предложение можно пред-
ставить расчетной схемой,
иллюстрация			которой
приведена на рис. 4.1. В
соответствии с этой схе-					Рис. 4.1. Предлагаемая расчетная схема дорож-
мой	покрытие		перерас-
пределяет нагрузку по по-					ной конструкции при расчете по сопротивле-
					нию сдвигу: 1 – наибольшая величина каса-
верхности		основания,		а	тельного напряжения; 2 – местоположение
основание		– земляного			наиболее опасной точки

полотна. В слое основания и земляном полотне возникают сжимающие главные напряжения –

максимальное 1 и минимальное 3. Применяя одну из модифицированных в гл. 2 моделей, можно рассчитать величину главных напря-

4 Александров А.С., Долгих Г.В., Калинин А.Л. О допускаемых давлениях на грунты земляного полотна и слои дорожной одежды // Наука и техника в дорожной отрасли. – 2012. – №2. – С. 10 – 13.

137

жений в каждой точке слоя основания или земляном полотне. Подставив главные напряжения в условия пластичности, например критерий Кулона – Мора, можно вычислить касательные напряжения, соответствующие этому критерию, и построить эпюру их изменения по глубине. На некоторой глубине касательное напряжение достигает наибольшей величины, которая на рис. 4.1 показана точкой 1. Этой глубине соответствует местоположение наиболее опасной точки, расположенной на оси симметрии нагрузки и показанной на рис. 4.1 точкой 2. Таким образом, нами предлагается иная расчетная схема по сравнению с физическими моделями А.М. Кривисского [30, 31] и нормативных документов [46, 47].

Для реализации представленной расчетной схемы и совершенствования метода необходим обоснованный выбор условия пластичности.

4.2. Модификация условия пластичности Кулона – Мора вводом параметра, учитывающего величину деформаций

Условие пластичности Кулона – Мора широко применяется для решения задач о сопротивлении сдвигу грунтов земляного полотна и оснований фундаментов. Параметры грунта c и этого условия пластичности определяются по данным испытаний, как правило, трехосного сжатия в стабилометре. Условием окончания испытания является разрушение образца грунта или его деформирование на требуемую предельную глубину. В качестве предельной деформации грунта в РФ принимают 15 % [16], а за рубежом 20 % [65, 73]. Отсюда следует, что при расчете земляных сооружений по сопротивлению сдвигу с использованием критерия Кулона – Мора в расчетной точке деформация грунта составит как минимум 15 %. Если расчетная точка является наиболее опасной, то деформация в ней будет наибольшей по сравнению с деформациями в других точках. Кроме несущей способности устойчивость грунтовых оснований характеризуется предельно допускаемыми осадками, а предельные необратимые смещения поверхности земляного полотна зависят от норм ровности покрытий. Например, глубина неровностей, формирующихся на поверхности асфальтобетонного покрытия, составляет 3 мм. В том случае если асфальтобетонное покрытие способно испытывать вертикальные остаточные деформации, то предельная величина смещения поверхности слоев основания из дискретных материалов будет иметь значение

138

меньше 3 мм. Предельные необратимые смещения поверхности земляного полотна должны иметь еще более низкие значения по сравнению с допускаемыми величинами для оснований дорожных одежд. Поэтому при диагностике автомобильных дорог нередко отмечают факт, когда срок службы, на который запроектирована дорожная конструкция по критерию сопротивления сдвигу, еще не выработан, а измеренная продольная или поперечная ровность вышла за рамки допускаемых значений. Отсюда следует, что предельное состояние по сопротивлению сдвигу наступает позже, чем отказ дорожной конструкции по ровности. По нашему мнению, это связано с тем, что при расчете земляного полотна по сопротивлению сдвигу с использованием условия Кулона – Мора трудно увязать деформацию в наиболее опасной точке, например 15 % с его предельной осадкой. Компенсировать этот недостаток можно расчетами дорожной конструкции по критериям продольной и поперечной ровности. Также возможен другой вариант проектирования, согласно которому в расчет дорожной конструкции по сопротивлению сдвигу можно заложить другое условие пластичности, по которому срок службы одинаковых дорожных одежд будет меньше, чем при применении критерия Кулона – Мора.

Мотивировать необходимость замены критерия Кулона – Мора другим условием пластичности можно двумя доводами, подтверждающимися данными экспериментов.

Во-первых, параметры предельной прямой Кулона – Мора определяются по данным трехосных испытаний. Условием отказа образца считается его разрушение или деформирование до предельной величины 1=15 % в РФ или 1=20 % в США и странах Евросоюза. Это значит, что если в элементе дорожной конструкции возникнет зона с предельным состоянием по критерию Кулона – Мора глубиной распространения всего 10 см, то она претерпит деформации величиной 15 – 20 мм. Такие деформации превышают предельные значения продольных неровностей и допускаемую глубину колеи.

Во-вторых, физическая природа появления площадок скольжения объясняется экспериментальными данными и состоит в том, что по линиям будущего сдвига происходит локализация деформаций [107]. В процессе воздействия нагрузки деформации накапливаются и проявляются в виде линии толщиной приблизительно в 10 зерен [108]. Эксперименты японских коллег показали, что площадки скольжения в грунтовом образце, изготовленном в форме параллелепипеда, зарождаются при деформации 1=8 % и развиваются в ходе деформирова-

139

ния до величины 1=12 % [91, 108]. При деформации образца 1=12 % площадки скольжения сформированы окончательно.

Мы считаем, что такое условие можно найти сравнением различных условий пластичности с критерием Кулона – Мора.

В первой части монографии5 приведены различные критерии прочности и условия пластичности, выполнен их анализ и сопоставление с критерием Кулона – Мора. Показано, что аппроксимация параметров материала в этих критериях сцеплением и углом внутреннего трения выполнена так, что их предельные поверхности сходятся с шестигранником Кулона – Мора в углах сжатия или расширения (критерии Друкера – Прагера, Ладе, Ладе – Дункана), или и в углах сжатия и в углах расширения (критерий Матцуока – Накаи).

Такое взаимное расположение предельных поверхностей аналитических критериев на девиаторной плоскости показано на рис. 4.2.

		Из анализа рис. 4.2 сле-
	дует, что при напряженном
	состоянии 1> 2= 3 анали-
	тические условия		пластич-
	ности грунтов дают такие же
	результаты, как и условие
	Кулона – Мора. Следова-
	тельно, замена критерия Ку-
	лона – Мора другим анали-
	тическим условием пластич-
	ности при напряженном со-
	стоянии 1> 2= 3		не приво-
	дит к изменению результа-
	тов расчета. Такая замена
	целесообразна при углах Ло-
Рис. 4.2. Критерии в девиаторном плане:	де, варьирующихся в диапа-
	зоне -30 о< <30		о, то есть
1– Кулона – Мора; 2 – Матцуока – Накаи;
	при так называемом истин-
3 – Ладе Дункана; 4 – Друкера – Прагера
при аппроксимации по углам сжатия по-	ном	трехосном	сжатии
верхности Мора	1> 2> 3.

В связи с таким взаимным расположением предельных поверхностей аналитических условий пластичности по отношению к шестиграннику Мора целесообразно рассматривать возможность примене-

5 Александров А.С. Совершенствование расчета дорожных конструкций по сопротивлению сдвигу Ч. 1. Состояние вопроса. – Омск : СибАДИ, 2015. – 292 с.

140

ния эмпирических критериев или критериев, полученных модификацией условий пластичности твердых тел, в которых пределы прочности заменены сцеплением и углом внутреннего трения. Рассмотрим уравнение предельного состояния третьей теории прочности, записанное для твердого тела и грунта. Для твердых тел и грунтов предельное состояние при сжатии по третьей теории прочности описывается уравнениями

1 3 Rс ;

1 3 2 cu ,

(4.2)

где Rс – предел прочности на одноосное сжатие, Па; cu – сопротивление недренированному сдвигу.

Предел прочности на одноосное сжатие определяется по формуле

R	2 c cos	,	(4.3)

с	1 sin

где с и – сцепление и угол внутреннего трения, определенные по данным КН испытаний в приборе трехосного сжатия.

Из анализа уравнений (4.2) следует, что при одинаковых значениях главных напряжений их левые части, называемые девиаторомd, равны. Тогда правые части уравнений (4.2) тоже должны быть равны между собой, что с учетом формулы (4.3) означает зависимость сопротивления недренированному сдвигу от параметров материала критерия Кулона – Мора. Это было бы так, если параметры с, и cu определялись бы из одного и того же испытания. В действительности сопротивление недренированному сдвигу определяется по данным НН трехосных испытаний, а сцепление и угол внутреннего трения

– из КН или КД трехосных испытаний. Это означает, что вместо равенства между пределом прочности на сжатие Rс И недренированной прочностью будет иметь место неравенство

c		c cos	.	(4.4)

u	1 sin

Однако вследствие того, что на каждом из кругов Мора, построенных по данным одного и того же испытания, можно взять как площадку с напряжениями Кулона – Мора, так и площадку с максимальным касательным напряжением, то можно к каждой этой точке провести касательную. Эти касательные представляют собой проекции шестигранника Треска и пирамиды Мора на - план. Поэтому можно определить как координаты касания этих прямых к кругу предельных напряжений, так и найти координаты точки их пересечения. Для пояснения сказанного мы на рис. 4.3 изобразили один из кругов Мора, к

141

двум точкам которого схематично провели две предельные прямые, которые являются в квадранте сжатия - плана проекцией предельных поверхностей Треска и Мора.

Рис. 4.3. Круг Мора и предельные прямые по третьей теории прочности и условию пластичности Кулона – Мора: 1 и 2 – проекции на - план призмы Треска и пирамиды Мора; 3 и 4 – точки касания предельных прямых условий третьей теории и Кулона – Мора к кругу напряжений; 5 – точка пересечения проекций поверхностей Треска и Мора

Прямая 1 является проекцией на плоскость - призмы Треска и касательной к точке 3, которая расположена на площадке, повернутой к главным осям под углом 45 0. Эта прямая определяет предельное состояние по третьей теории прочности для одного из кругов Мора. Уравнение такого предельного состояния можно представить формулой

1 3 2 cT ,

(4.5)

где cT – сцепление Треска, Па.

Также на рис. 4.3 приведена прямая 2, являющаяся на - плане следом пирамиды Мора и касательной к точке 4. Уравнение этой прямой можно дать в виде

	c tg .				(4.6)
Если в формуле (4.6) и записать в главных напряжениях, то
получим уравнение предельного состояния Кулона – Мора
	1 3		1 3	tg c.	(4.7)
	2 cos
		2

142

Выразив из (4.7) девиатор, получим уравнение

					3
	3	2 cos c	1		3	tg .	(4.8)
		2 cos c				tg .	(4.8)
1				2
				2

Левые части критериев (4.5) и (4.8) равны, вследствие чего сцепление Треска определяется по формуле

				3
c	cos c	1		3	tg .	(4.9)
c	cos c				tg .	(4.9)
T			2
			2

Подставив зависимость (4.9) в уравнение предельного состояния (4.5), получим формулу (4.8).

В свою очередь, преобразуя зависимость (4.8), получим уравнение предельного состояния Кулона – Мора (4.7). Из выражения (4.9) сцепление Кулона – Мора сС–М=с определяется по формуле


		c		cT			1 3		tg .				(4.10)
				cos
						2
Подстановкой выражения (4.10) в уравнение предельного состоя-
ния Кулона – Мора (4.7) можно получить зависимость
	1 3		1 3		tg			cT			1 3	tg .	(4.11)
	2 cos							cos
		2								2

Выражение (4.11) преобразуется в уравнение предельного состояния (4.5). Таким образом, полученные зависимости (4.9) и (4.10) позволяют выполнять переход от третьей теории прочности к условию Кулона – Мора и наоборот. Из анализа зависимости (4.9) следует, что величина сцепления Треска соответствует радиусу круга предельных напряжений Мора. Для каждого из построенных кругов Мора величина сТ индивидуальна. Вследствие чего для каждой пары предельных главных напряжений существует своя величина сТ, зависящая от сцепления и угла внутреннего трения. Поэтому при расчете сцепления Треска по формуле (4.9) между результатами вычислений по критериям (4.5) и (4.7) количественной разницы нет.

Предел прочности на одноосное сжатие или растяжение для третьей теории прочности связан со сцеплением Треска зависимостью

Rс Rр 2 cT .

(4.12)

В критерии Мора пределы прочности на сжатие и растяжение неодинаковы, вследствие чего связаны со сцеплением и углом внутреннего трения разными формулами. Предел прочности на сжатие определяется зависимостью (4.3), а предел прочности на растяжение находится по формуле

143

R	2 c cos	.	(4.13)

р	1 sin

Принимая связь предела прочности на сжатие с параметрами материала условия пластичности Кулона – Мора по (4.3) и (4.12), получим

c		c cos	.	(4.14)

T	1 sin

Зависимость (4.14) не учитывает величину главных напряжений, то есть при любых значениях 1 и 3 величина сТ одинакова. Результаты расчета по формулам (4.9) и (4.14) совпадают, если в зависимости (4.9) 3=0, то есть при одноосном сжатии. В этом случае предельная величина 1= 1пр является прочностью на одноосное сжатие1пр =Rc=cons’t, а зависимость (4.9) дает один и тот же результат и преобразуется в выражение (4.14). Подставив зависимость (4.10) в условие (4.5), уравнение предельного состояния можно дать в виде

1 3	1 sin	c.	(4.15)
2
	cos

Несложно показать, что выражение (4.15) вытекает из решения классической задачи о точке пересечения двух прямых, для решения которой из уравнений (4.5) и (4.15) достаточно составить систему. Эта система уравнений имеет вид

1 3	c	0

2	T			(4.16)
			.
c cos	c	0

1 sin	T

Решением системы уравнений (4.16) является зависимость (4.15). Величина касательных напряжений, вычисляемых по левой части формулы (4.15), получается выше, чем касательные напряжения, определяемые по левой части условия (4.7). Если для одинаковых удерживающих напряжений 3 из выражений (4.7) и (4.15) вычислить предельные максимальные напряжения 1, то можно убедиться в том, что предельная величина напряжения 1 в условии Кулона – Мора (4.7) больше, чем в уравнении предельного состояния (4.15).

Применяя формулы (4.3), (4.9) и (4.13) и параметры предельной прямой Кулона – Мора, регламентируемые ОДН 218.046-01, можно вычислить прочность на одноосное сжатие, сцепление Треска и прочность на одноосное сжатие для различных грунтов.

144

Оригинальный критерий Мора для твердого тела запишем в виде

σ1 kM σ3 Rр; kM Rр Rс . (4.17)

Критерий (4.17) описывает предельное состояние по критерию Мора при растяжении. Для сжатия этот критерий запишем в виде

σ1 kM σ3 Rc ;					kM Rс Rр .				(4.18)
Подставив во вторую зависимость формул (4.18) выражения (4.3)
и (4.13), получим зависимость коэффициента kM от :
		kM		1 sin			.		(4.19)

				1 sin
Подставив в условие пластичности (4.18) выражения (4.3) и
(4.19), получим уравнение			1 sin			2 c cos
σ	σ	3						.	(4.20)
			1 sin
1						1 sin
Выполнив в уравнении (4.20) преобразования, получим
σ1 1 sin σ3 1 sin 2 c cos .									(4.21)
Раскрыв в выражении (4.21) скобки, получим
σ1 σ1	sin σ3 σ3 sin 2 c cos .								(4.22)
Вынеся в зависимости (4.22) главные напряжения за скобки, по-
лучим
σ1 1 sin σ3 1 sin 2 c cos .									(4.23)

Условие (4.23) является одной из возможных форм записи критерия Кулона – Мора. Такую форму записи условия пластичности Кулона – Мора приводит Р.Ф. Црайг [75]. Если в формуле (4.22) выполнить иную группировку членов, включающих в себя главные напряжения, то можно получить

σ1 σ3 σ1 σ3 sin 2 c cos .

(4.24)

Уравнение (4.24) приводится к формуле (4.7), являющейся традиционной для специалистов дорожной отрасли формой записи условия Кулона – Мора.

Выполненные нами преобразования (4.17) – (4.24) показывают, что при подстановке зависимостей (4.3) и (4.14) в аналитические критерии прочности твердых тел, вырождающиеся в условие Кулона – Мора, после соответствующих преобразований будет получено условие пластичности Кулона – Мора (4.7) или его другие формы записи. Поэтому такая модификация не приводит к критерию, в котором касательные напряжения превышают вычисляемые по левой части уравнения (4.7) значения. Следовательно, этот путь модификации не

145

дает возможности получить более жесткое условие пластичности. Однако для модификации классических теорий прочности, включающих в себя только один параметр материала, зависимости (4.3) и (4.14) вполне пригодны.

Подстановка в классические критерии прочности предела прочности на сжатие, определяемого по формуле (4.3), приводит к условиям, представленным в табл. 4.1.

Таблица 4.1. Модифицированные подстановкой формулы предела

прочности на сжатие (4.3), полученной из условия Кулона – Мора, критерии при напряженном состоянии 1> 2= 3

Критерий				Уравнение предельного равновесия
Критерий	в оригинальном виде				в модифицированном виде
	в оригинальном виде				в модифицированном виде
Критерий Г.									1 sin
Галилея			1 Rс					1					c
Галилея			1 Rс					1	2 cos				c
Критерий Э.						1		2 3				1 sin
Мариотта	1	2 3 Rс														c
	1	2 3 Rс														c
								2 cos
Критерий								1 3			1 sin				c;
Критерий								2							c;
Треска – Куло-		1	3	Rс				2				cos
на – Сен-		1	3	Rс			1	3		1		3		tg c
на – Сен-							1	3		1		3
Венана – Леви
Венана – Леви							2 cos					2
							2 cos					2
Критерий Гу-								1 3			1 sin				c;
															c;
		1	3	Rс				2				cos
бера – Мизеса								2				cos
бера – Мизеса							1	3		1		3
– Генки							1	3		1		3		tg c
– Генки														tg c
							2 cos					2

В модифицированных критериях табл. 4.1 в качестве параметров материала используются сцепление и угол внутреннего трения, вследствие чего предельные состояния по этим критериям находятся в различных точках предельной прямой Кулона – Мора. Эта предельная прямая не пересекает круг предельных напряжений, что означает соблюдение постулата Друкера о выпуклости поверхности пластичности.

Можно показать, что традиционные аналитические условия пластичности грунтов, в которых параметры материала аппроксимируются через сцепление и угол внутреннего трения, также не позволяют получить более строгое по сравнению с критерием Кулона – Мора условие. Критерий Друкера – Прагера [78, с. 157] имеет вид

146

J2 а I k ,

(4.25)

где J2 – второй инвариант девиатора напряжений, Па2; I1 – первый инвариант тензора напряжений, Па; а и k – параметры прочности.

В работе Д. Друкера и В. Прагера правило знаков принято обратное (растяжение плюс, а сжатие минус). Поэтому формулу (4.25) можно считать оригинальным условием Друкера – Прагера для растяжения. Приняв обратное правило знаков, критерий (4.25) примет вид

J2 а I k.

(4.26)

Уравнение предельного состояния (4.26) является традиционной формой записи условия пластичности Друкера – Прагера для грунтов [5]. Параметры материала в условиях (4.25) и (4.26) аппроксимируют формулами

a	2 sin		k	6 c cos
		;				.	(4.27)
	3 sin				3 sin
				3

При возникновении напряженного состояния, характеризующегося условием 1> 2= 3, условие Друкера – Прагера для сжатия и растяжения примет вид

1 3		2 sin		2		6 c cos	.	(4.28)

3	3 sin					3 3 sin
			1		3
1 3		2 sin		2		6 c cos	.	(4.29)

3	3 sin		1		3	3 3 sin

Введя в обе части уравнений (4.28) и (4.29) множитель sin-1 и выполнив преобразования, получим формулы

	1 3	sin .		(4.30)
	2 c ctg 1 3

1 3 3 sin			sin .	(4.31)

6 c ctg 2 1 4 3

Уравнение (4.30) известно как одна из форм записи условия Кулона – Мора. Поэтому при 1> 2= 3 условия Друкера – Прагера и Кулона – Мора являются тождественными, что продемонстрировано нами на рис. 4.2.

Безусловно, что для любого минимального главного напряжения будет существовать определенная величина максимального главного напряжения, при котором материал либо разрушается, либо его де-

147

формация достигает предельной величины. Обозначив эту предельную величину максимального главного напряжения 1пр и решив относительно нее уравнение (4.30), получим формулу

1пр	2 c cos 3	1 sin
			.	(4.32)

	1 sin

Аналогичную формулу приводит М. Хуурман [94, с. 108], обозначая 3 как conf, под которой понимается удерживающее напряжение (confining stress). Формула (4.32) позволяет определить величину максимального главного напряжения 1, при возникновении которого в условиях, заданных 2= 3, грунт с параметрами с и испытывает предельное состояние. При одноосном сжатии 2= 3=0. Тогда прочность дискретного материала при одноосном сжатии определяется по формуле

R	2 c cos	.	(4.33)

c	1 sin

Зависимость (4.33) тождественна формуле (4.3).

По аналогии с решением (4.32) в критерий (4.31) введем обозначение 1пр. Выразив его из уравнения (4.31), получим формулу

	2 c cos 3	1 sin
1пред			.	(4.34)

	1 sin

Принимая в зависимости (4.34) 3=0, получим формулу

R	2 c cos	.	(4.35)

р	1 sin

Формула (4.35) тождественна выражению (4.13).

Таким образом, формулы, связывающие пределы прочности на сжатие с углом внутреннего трения и сцеплением, полученные из критерия Друкера – Прагера, записанного для сжатия и растяжения, идентичны зависимостям (4.3) и (4.13), которые выведены из критерия Кулона – Мора. Следовательно, подстановка (4.33) и (4.35) в аналитические критерии прочности, приведет к их вырождению в оригинальное условие Кулона – Мора. Выполненный нами анализ показывает, что модификация аналитических критериев прочности твердых тел подстановкой в них зависимостей пределов прочности на сжатие и растяжение от сцепления и угла внутреннего трения, полученных из критерия Кулона – Мора или Друкера – Прагера, нецелесообразна. Нецелесообразность такого подхода состоит в том, что предпринимая попытку модификации критерия прочности, мы приходим к ориги-

148

нальному условию пластичности Кулона – Мора. В этом случае для осевого трехосного сжатия, характеризуемого главными напряжениями 1> 2= 3, поверхности модифицированных таким образом условий пластичности сходятся в углах сжатия шестигранника Мора подобно тому, как это имеет место при использовании оригинальных условий пластичности с параметрами материала, аппроксимируемыми через сцепление и угол внутреннего трения (рис. 4.2). Следовательно, для поиска более жесткого по сравнению с критерием Кулона

– Мора условия пластичности необходимо использовать другой подход. Одним из таких подходов может быть применение эмпирических условий пластичности, в которых касательное напряжение больше касательного напряжения критерия Кулона – Мора. Другой подход может заключаться в модификации критериев прочности твердых тел подстановкой в них зависимостей пределов прочности на сжатие и растяжение от параметров предельной прямой Кулона – Мора, результаты расчета по которым отличны хотя бы от одной из формул

(4.3) или (4.14).

Среди эмпирических условий пластичности можно выделить критерий Г. Арнольда [63]. Отметим, что известны некоторые интерпретации условия Кулона – Мора. Р.Ф. Црайг, применяя теорию Ренкина и условие Кулона – Мора, для решения задачи предельного равновесия показал, что альтернативой величине tan2( /4- /2) является зависимость (1-sin )/(1+sin ) [75]. Для определения предельной величины максимального главного напряжения при активном ренкиновском состояния Р.Ф. Црайг рекомендует использовать формулу [75]:

	2 c	1 sin		1	sin	σ		.	(4.36)
		1 sin
1пр			1		sin		3

Для определения предельной величины главного напряжения 3пр Р.Ф. Црайг рекомендует формулы:

1. Для области грунтового полупространства с активным ренкиновским состоянием

3пр 1 Kакт 2 с Kакт ,

(4.37)

где Kакт – коэффициент, являющийся функцией угла внутреннего трения для активного ренкиновского состояния.

2. Для области грунтового полупространства с пассивным ренкиновским состоянием

3пр 1 Kп 2 с Kп ,

(4.38)

149

где Kп – коэффициент, являющийся функцией угла внутреннего трения для пассивного ренкиновского состояния.

3. Для области грунтового полупространства с упругим состояни-

ем

3пр 1 K0 ,

(4.39)

где K0 – коэффициент, являющийся функцией угла внутреннего трения для зоны с упругим состоянием грунта.

Величина коэффициентов Kакт, Kп и K0 определяется по формулам

Kакт		1	sin	;	Kп		1	sin	; K	0 1 sin .	(4.40)

	1		sin			1		sin

В области с активным ренкиновским состоянием относят зону, в которой грунт в поперечном направлении расширяется [56], а в области с пассивным ренкиновским состоянием грунт в поперечном направлении сжимается.

	Эту работу грунта мо-
	делируют в приборах трех-
	осного сжатия. При таких
	испытаниях образец в по-
	перечном	направлении
	расширяется, если прило-
	женные главные напряже-
	ния соответствуют правилу
	1> 2= 3 (см. рис. 4.4 обра-
	зец справа). Наоборот, для
	сжатия образца в попереч-
	ном направлении необхо-
Рис. 4.4. Общий вид образцов из глины, ис-	димо прикладывать напря-
пытанных при боковом сжатии 1< 2= 3 и	жения,	подчиняющиеся
расширении 1> 2= 3 [77]	правилу 1< 2= 3 (рис. 4.4,
	образец слева).

Г.К. Арнольд, выполнив анализ результатов трехосных испытаний, пришел к выводу, что предельное состояние наступает при несколько меньшей величине максимального главного напряжения, чем это следует из условия Кулона – Мора, и в частности формулы (4.36). Вследствие этого предельная величина удерживающего напряжения должна быть выше, чем это следует из формулы (4.37). Учитывая эти обстоятельства, Г.К. Арнольд формулы (4.37) и (4.38) дает в виде

150

3пр 1 Kакт	2 с Kакт.	(4.41)
3пр 1 Kп	2 с Kп .	(4.42)

Сравнивая зависимости (4.41) и (4.42) с формулами (4.37) и (4.38), несложно заметить, что в вычитаемых представлениях Г.К. Арнольда корни квадратные из коэффициентов Kакт и Kп возведены в квадрат. Это позволяет уменьшить вычитаемое и увеличить предельную величину минимального главного напряжения 3пр в зависимости (4.41) по сравнению с формулой (4.37), полученной из классического критерия Кулона – Мора. В зависимостях (4.38) и (4.42) напряжение3> 1, поэтому эти зависимости определяют предельную величину не минимального главного, а максимального главного напряжения. В зависимости (4.42) вычитаемое имеет большее значение по сравнению с вычитаемым в традиционной формуле (4.38). Поэтому величина 3пр, вычисляемая по выражению Г.К. Арнольда (4.42), меньше чем ее аналог, рассчитываемый по формуле (4.38).

В сечении, расположенном по оси симметрии нагрузки, грунт испытывает поперечные деформации расширения, вследствие чего работает в условиях активного ренкиновского состояния. Поэтому для специалистов дорожной отрасли наибольший интерес представляет сравнительный анализ формул (4.37) и (4.41). Из зависимости (4.37) можно получить одну из основных форм уравнения предельного состояния по условию пластичности Кулона – Мора. Это уравнение имеет вид

1		1 sin		1 sin
	1		3		с.	(4.43)

2		1 sin
				1 sin

Касательные напряжения, определяемые левой частью уравнения (4.43), равны касательным напряжениям, вычисляемым по (4.7) или (4.24). Поэтому, несмотря на различные формы записи, (4.7) и (4.43) идентичны. Аналогично из зависимости (4.41) можно выразить уравнение предельного состояния, соответствующее предложению Г.К. Арнольда. Это уравнение назовем условием пластичности Г.К. Арнольда и запишем его в виде

1		1 sin		с.	(4.44)

2
	1	1 sin	3

Анализируя (4.44), несложно заметить, что касательные напряжения, определяемые левой частью этого критерия, имеют значения, превышающие касательные напряжения по условию Кулона–Мора,

151

определяемые левой частью условия (4.43). Таким образом, критерий Г.К. Арнольда является более жестким условием пластичности по сравнению с критерием Кулона – Мора. Безусловно, что предельное состояние по (4.44) наступит при деформировании образца на меньшую величину по сравнению с деформацией 15 %, которая является условием отказа образца по критерию Кулона – Мора. Поэтому, несмотря на отсутствие какого-либо аналитического обоснования возможности изменения зависимости (4.37) и ее представления в виде формулы (4.41), предложение Г.К. Арнольда заслуживает серьезного внимания. Кроме того, Г.К. Арнольд сформулировал свое предложение в виде представлений (4.41) и (4.42), анализируя данные трехосных испытаний грунтов. Поэтому условие предельного равновесия (4.44) следует считать эмпирическим критерием, вывод которого требует применения методов математической статистики и не нуждается в каком-либо другом обосновании, в том числе аналитическом реше-

нии. При 3=0 условие (4.44) принимает вид
1 2 с.	(4.45)
Безусловно, что (4.45) равносильно тому, что
Rс 2 cT .	(4.46)

Таким образом, при одноосном сжатии критерий Г.К. Арнольда тождественен третьей теории прочности. Формула (4.46) позволяет модифицировать классические теории прочности. Результаты такой модификации приведены в табл. 4.2.

Таблица 4.2. Модифицированные подстановкой формулы предела

прочности на сжатие, полученной из условия Г.К. Арнольда, критерии при напряженном состоянии 1> 2= 3

Критерий		Уравнение предельного равновесия
	в оригинальном виде			в модифицированном виде

Критерий Г. Гали-		1 Rс			1 2 cT
лея
Критерий Э. Мари-	1 2 3 Rс			1 2 3 2 cT
отта
Критерий Треска –	1	3	Rс	1	3	2 cT
Кулона – Сен-
Венана – Леви
Критерий Губера –	1	3	Rс	1	3	2 cT
Мизеса – Генки

Из анализа данных следует, что при напряженном состоянии1> 2= 3 четвертая теория прочности принимает вид третьей теории,

152

в которую также вырождается критерий Кулона – Мора при Rс=Rр. В первой и второй теории при 2= 3 0 величина девиатора завышена по сравнению с другими критериями. Область применения представления предела прочности на сжатие, полученного из условия Г.К. Арнольда, ограничена вариантами, показанными в табл. 4.2.

В работах японских специалистов выполнены исследования вопроса зарождения и развития площадок сдвига, формирующихся в образцах глинистого грунта при трехосных испытаниях [91, 92, 108]. В результате установлено, что причиной появления площадок скольжения являются пластические деформации, локализующиеся вдоль них [92, 107]. Начало локализации деформаций происходит при деформировании образца в вертикальном направлении, то есть в направлении действия максимального главного напряжения, на 8 %. Такая деформация соответствует моменту зарождения площадок скольжения [91, 91, 108]. При деформировании образца до 12 % формирование площадок завершено, а от каждого угла прямоугольного образца формируются четыре площадки сдвига. При дальнейшем деформировании образец либо течет, либо разрушается сдвигом по одной из сформированных ранее площадок сдвига [108].

А.Л. Калинин развил идею Г.К. Арнольда и ввел в его критерий третий параметр, предполагая, что таким образом удастся связать предельное состояние модифицированного критерия с деформацией образца при трехосном сжатии. По А.Л. Калинину, предельное состояние грунта описывается уравнениями

1		1 sin				1 sin	с.	(4.47)
					В
2		1 sin				1 sin
	1			3
1		1 sin			1 sin b
							с,	(4.48)
2		1 sin
	1		3		1 sin

где В и b – параметры материала, определяемые экспериментально.

Вторая форма записи условия Калинина (4.48) является более удобной. Из анализа этой зависимости следует, что при b=0,5 условие пластичности (4.48) принимает вид критерия Кулона – Мора (4.43). При b=0 условие (4.48) становится критерием Г.К. Арнольда (4.44). Отсюда следует, что при увеличении параметра b в уравнении предельного состояния (4.48) отказ по этому критерию будет наступать при более высоких деформациях, фиксируемых при трехосных испытаниях. Принимая в уравнении (4.43) минимальное главное напряже-

153

ние равным нулю, то есть 3=0, из этого критерия можно получить зависимость предела прочности на одноосное сжатие от параметров предельной прямой Кулона – Мора. Если в уравнениях (4.44) и (4.48) принять такое же условие 3=0, то из этих критериев можно получить аналоги предела прочности при одноосном сжатии. Под аналогом предела прочности при одноосном сжатии понимается величина напряжения, при котором образец не испытывает разрушения и его деформация меньше деформации 15 % или деформации, при которой образец разрушился. Аналогично можно определить предел прочности на одноосное растяжение и его аналоги. Такие зависимости могут представлять интерес при модификации критериев прочности твердых тел.

В настоящей работе продемонстрируем несколько иной путь модификации оригинального условия Мора. Формулы для расчета пределов прочности на сжатие (4.3) и растяжение (4.14), полученные из критерия Кулона – Мора, или идентичные им зависимости (4.33) и (4.35), выведенные из условия Друкера – Прагера, можно записать в виде6

2 c cos

2 с

1 sin

(4.49)

1 sin

2 c cos

2 с

1 sin

(4.50)

1 sin

Введя в эти зависимости параметр d, получим

1 sin d

Rc 2 с . (4.51)

1 sin

1 sin d

Rр 2 с . (4.52)

1 sin

Из анализа формул (4.51) и (4.52) следует, что в зависимости от величины d сопротивления сжатию и растяжению имеют диапазон варьирования, границами которого являются пределы прочности третьей теории и гипотезы Мора. При подстановке в зависимости

(4.51) и (4.52) d=0,5 они приобретают вид формул (4.49) и (4.50). Если в зависимости (4.51) и (4.52) подставить d=0, то эти выражения становятся третьей теорией прочности. На рис. 4.5 и 4.6 приведены зависи-

6 Тождества (4.49) и (4.50) из основного свойства тригонометрии прямоугольных треуголь-

ников, а именно cos2 +sin2 =1. Отсюда следует, что cos =(1+sin )0,5 (1-sin )0,5.

154

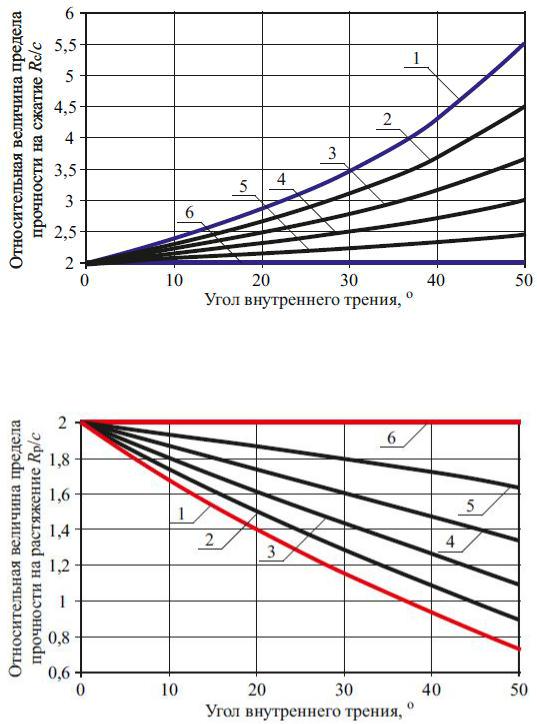
мости пределов прочности на сжатие и растяжение, выраженные в долях сцепления, от угла внутреннего трения и параметра d.

Рис. 4.5. Зависимость предела прочности на сжатие, выраженного в долях сцепления от угла внутреннего трения: 1 – по условию Кулона – Мора, Друкера

– Прагера и формуле (4.51) при d=0,5; 2–5 – по формуле (4.51) при d=0,4; 0,3; 0,2

и 0,1 соответственно; 6 – по третьей теории прочности и формуле (4.51) при d=0

Рис. 4.6. Зависимость предела прочности на растяжение, выраженного в долях сцепления от угла внутреннего трения: 1 – по условию Кулона – Мора, Друкера

– Прагера и формуле (4.52) при d=0,5; 2–5 – по формуле (4.52) при d=0,4; 0,3; 0,2

и 0,1 соответственно; 6 – по третьей теории прочности и формуле (4.52) при d=0

155

Подставив во вторую зависимость (4.18) формулы (4.51) и (4.52), получим

sin d

2 с

2 d

1 sin

sin

1 sin

. (4.53)

sin d

1 sin

2 с

sin

Тогда с учетом зависимости (4.53) модифицированный критерий Мора получим в виде одного из двух тождественных уравнений

1		1 sin 2 d				1	sin d
	σ			σ						с.	(4.54)
2	σ			σ						с.	(4.54)
2	1	1 sin			3	1	sin

1		1	sin d	1 sin d
	σ							σ		с.	(4.55)
2	σ							σ		с.	(4.55)
2	1	1	sin	1 sin					3

При d=0,5 уравнение (4.55) приобретает вид тождества (4.43), то есть становится критерием Кулона – Мора. При d=0 зависимость (4.55) превращается в третью теорию прочности. Таким образом, критерий (4.55) при d=0 не тождественен уравнению (4.48), которое при d=0 приобретает вид критерия Г.К. Арнольда (4.44). Следовательно, критерий (4.55) обобщает критерий А.Л. Калинина. Рассмотрим применение формул (4.51) и (4.52) к модификации некоторых критериев прочности твердых тел (табл. 4.3).

Таблица 4.3. Модифицированные подстановкой формул (4.51) и (4.52)

критерии при напряженном состоянии 1> 2= 3

Критерий

Уравнение предельного равновесия

в оригинальном

в модифицированном виде

виде

Критерий Г. Га-

1 Rс

1 sin d

лилея

1 sin

Критерий Э.

1 2 3 Rс

1 sin d

Мариотта

1 sin

Критерий Трес-

1 sin d

ка – Кулона –

1 3 Rс

Сен-Венана –

1 sin

Леви

156

Окончание табл. 4.3

Критерий Гу-

Rс

1 sin d

бера–Мизеса–

Генки

1 sin

Критерий

1 и 2 Rс

1 sin d

с,

В.П. Сдобыре-

1 sin

ва

где и

– интенсивность нормальных напряжений Р. Мизеса

1 и

1 2 R

1 и

1 sin d

1 2

с,

ср

Критерий И.И.

1 sin

1 и

Трунина

где α – параметр материала, определяемый опытным путем

(0<α≤1); –параметр напряженного состояния, ср – всесторон-

нее равномерное (среднее) напряжение, Па

Критерий

1 sin

Мора

σ1

σ3

для сжатия

Rр

1 sin

Критерий

Rр

1 sin d

1 sin

Мора

1 sin

для растяжения

Аналогичным образом модифицируются другие критерии прочности твердых тел. В работе7 автором совместно с Г.В. Долгих и А.Л. Калининым рассмотрена возможность модификации критериев прочности твердых тел вводом в них зависимостей пределов прочности на сжатие и растяжение, полученных из условия пластичности Друкера – Прагера. В этой работе применен другой принцип вывода формул для расчета пределов прочности на сжатие и растяжение, отличающийся от представленного автором при выводе формул (4.33) и (4.35) способа. В основу этого способа положена работа Г.Г. Болдырева [5], в соответствии с которой критерий Друкера – Прагера принимается в одинаковой форме для сжатия и растяжения, а именно в виде уравнения (4.26). Аппроксимация параметров материала в этом критерии производится по формулам (4.27) при разных знаках в знаменателе. Модифицированные в этой работе критерии анализирова-

7 Александров А.С., Долгих Г.В., Калинин А.Л. Применение критерия Друкера – Прагера для модификации условий пластичности // Наука и техника в дорожной отрасли. – 2013. – №2.

– С.26 – 29.

157

лись А.Л. Калининым [24] и сравнивались с данными трехосных испытаний Г.В. Долгих [17]. В итоге Г.В. Долгих установил, что наиболее пригодным является критерий А.К. Арнольда [63].

Отметим, что критерий (4.55) охватывает достаточно большой диапазон возможных решений задачи о начале пластичности. Поэтому этот критерий, а также условия Кулона – Мора, Г.К. Арнольда и А.Л. Калинина примем для дальнейшего анализа и сопоставления с данными эксперимента.

В рассматриваемых нами модифицированных и эмпирических условиях пластичности параметры материала описываются сцеплением и углом внутреннего трения, которые могут быть связаны со сцеплением Треска. Через параметры предельной прямой Кулона – Мора выражаются пределы прочности на сжатие и растяжение, но для каждого критерия такие выражения являются индивидуальными. Кроме того, для каждого критерия может быть выражена предельная величина максимального главного напряжения, при которой по данному критерию в условиях трехосного сжатия или растяжения происходит отказ материала по принятому условию пластичности. Эту предельную величину максимального главного напряжения можно выразить через параметры материала. Зависимость (4.32) связывает предельное значение максимального главного напряжения по условию Кулона – Мора с углом внутреннего трения для трехосного сжатия. Представим формулу (4.32) в виде

	2 c cos			1	sin	.	(4.56)

1пр	1 sin	3	1		sin

Из совместного анализа зависимостей (4.56) и (4.49) следует, что предельная величина максимального главного напряжения в условии Кулона – Мора может быть представлена через предел прочности материала на сжатие. Подставив в зависимость (4.56) формулы (4.33) и (4.50), получим

			3	R	2
	R			с		.	(4.57)

1пр	с	4 c2

В формуле (4.57) предельная величина максимального главного напряжения является аналогом предела прочности при трехосном сжатии напряжениями 1> 2= 3, связанного с пределом прочности при одноосном сжатии, соответствующем критерию Кулона. Аналогичную связь можно получить для всестороннего растяжения. Для этого зависимость (4.34), полученную нами из критерия Друкера –

158

Прагера, тождественного условию пластичности Кулона – Мора, представим в виде

	2 c cos			1	sin	.	(4.58)

1пр	1 sin	3	1		sin

Подставив в (4.58) формулы (4.50), получим

			3	R	2
	R			р		.	(4.59)

1пр	р	4 с2

Формулы (4.57) и (4.59) так же, как тождественные им зависимости (4.56) и (4.58), справедливы только для критерия Кулона–Мора и других теорий прочности, которые при 1> 2= 3 вырождаются в условие пластичности Кулона–Мора, например критериев Друкера – Прагера, Писаренко – Лебедева, Надаи и т.п. Для других критериев можно вывести аналогичные зависимостям (4.56) – (4.59) формулы, но эти выражения будут приводить к другим результатам расчета.

Решив предлагаемое нами уравнение предельного состояния (4.55) относительно величины 1пр, получим

sin d

sin

2 d

1пр

2 с

σ3.

(4.60)

sin

Из анализа зависимости (4.60) следует, что:

– при d=0 это уравнение приобретает вид третьей теории прочно-

сти

1пр 2 с σ3;

(4.61)

– при d=0,5 это уравнение приобретает вид теории Кулона – Мо-

ра

	2 с	1 sin		1	sin	σ	3	.	(4.62)
		1 sin
1пр			1		sin

Из сравнительного анализа зависимостей (4.60) – (4.62) следует, что вычисляемая по формуле (4.60) предельная величина максимального главного напряжения при любой величине параметра d, варьирующегося в диапазоне 0<d<0,5, больше чем по формуле (4.61) и меньше чем по выражению (4.62). Отсюда следует, что каждой величине d соответствует индивидуальный круг предельных напряжений. В табл. 4.4 приведены вычисленные для заданных значений 3 параметры предельных кругов Мора.

159

Таблица 4.4. Параметры кругов предельных напряжений при различной

величине параметра d и минимальных главных напряжениях 3

Характеристика			Величина
Напряжение 3, кПа		50	100	150	200
Угол внутреннего трения , град		20	20	20	20
Сцепление с, кПа		30	30	30	30
Предельная величина максималь-	d=0,5	187,669	289,650	391,630	493,610
Предельная величина максималь-	d=0,4	168,225	256,657	345,089	433,520
ного главного напряжения, вы-	d=0,3	150,987	227,670	304,353	381,036
численная по формуле (4.84),	d=0,2	135,688	202,183	268,678	335,172
кПа, при	d=0,1	122,093	179,754	237,414	295,075
	d=0	110	160	210	260
	d=0,5	68,835	94,825	120,815	146,805
Радиус кругов предельных на-	d=0,4	59,113	78,329	97,545	116,760
Радиус кругов предельных на-	d=0,3	50,494	63,835	77,177	90,518
пряжений, кПа, при	d=0,2	42,844	51,092	59,339	67,586
	d=0,1	36,047	39,877	43,707	47,538
	d=0	30	30	30	30
	d=0,5	118,835	194,825	270,815	346,805
Абсцисса центра кругов предель-	d=0,4	109,113	178,329	247,545	316,760
Абсцисса центра кругов предель-	d=0,3	100,494	163,835	227,177	290,518
ных напряжений, кПа, при	d=0,2	92,844	151,092	209,339	267,586
	d=0,1	86,047	139,877	193,707	247,538
	d=0	80	130	180	230
Сцепление Треска	(4.9)	68,835	94,825	120,815	146,805
Сцепление Треска	(4.14)	42,844	42,844	42,844	42,844
	(4.14)	42,844	42,844	42,844	42,844

Примечание. Сцепление Треска по формуле (4.9) вычислено при подстановке вместо 1 величины 1пр, рассчитанной по формуле (4.60) при d=0,5, то есть для случая, когда уравнение (4.60) тождественно зависимостям (4.32), (4.56).

На рис. 4.7 приведены построенные по данным табл. 4.4 круги предельных напряжений. Из анализа данных табл. 4.4 и рис. 4.7 следует, что в уравнении предельного состояния (4.55) каждой величине параметра d соответствует круг предельных напряжений. При этом условие (4.55) постулирует постоянство сцепления, то есть с=cons’t для всех кругов Мора. Это наглядно представлено на рис. 4.8, а также данными табл. 4.9, в соответствии с которыми радиус круга Мора при d=0 равен сцеплению Кулона – Мора. Из анализа предельных прямых (см. рис. 4.7), проведенных к соответствующим кругам предельных напряжений, следует, что угловая координата в уравнениях прямых изменяется от величины, соответствующей углу внутреннего трения Кулона – Мора, при d=0,5 до =0 при d=0. Отсюда следует, что пара-

160

метр d в уравнении предельного равновесия (4.55) регулирует размеры круга предельных напряжений и угол наклона касательной к ним. При вариации параметра d в диапазоне 0<d<0,5 все предельные поверхности заключены между шестигранниками Треска (случай d=0) и Мора (случай d=0,5). Таким образом, условие пластичности (4.55) является мультиповерхностным критерием. Если уравнение (4.55) модифицировать вводом угла Лоде, то можно построить мультиповерхностное условие пластичности, которое применимо при любых напряженных состояниях. Однако вследствие того, что при расчетах дорожных конструкций принято напряженное состояние, характеризуемое напряжениями 1> 2= 3, то уравнения (4.55) вполне достаточно так, как оно описывает именно это напряженное состояние.

Рис. 4.7. Круги предельных напряжений по данным табл. 4.9:

1–3 при 3=50 кПа и d 0,5; 0,3 и 0; 4–6 при 3=200 кПа и d 0,5; 0,3 и 0

В процессе трехосных испытаний при постоянном минимальном главном напряжении к образцу прикладываются различные постоянно увеличивающиеся максимальные главные напряжения, обуславливающие рост деформации. Поэтому каждой величине напряжения 1 при постоянном напряжении 3 соответствует определенная деформация образца. Сопоставление результатов расчета по формуле (4.60) с экспериментальными максимальными главными напряжениями позволяет определить величину деформации, соответствующую предельному напряжению, вычисленному по зависимости (4.60) при определенном параметре d. Отсюда следует, что задаваясь предельной

161

деформацией, можно определить величину параметра d. В этом случае уравнение предельного состояния (4.55) будет связано с предельной деформацией, значение которой будет меньше 15 %.

4.3. Экспериментальная оценка условий пластичности при трехосных испытаниях грунтов

Трехосные испытания грунтов связывают с именем Артура Касагранде [88]. А. Касагранде одним из первых пришел к выводу, что поровое давление развивается только в условиях оттока воды из образца. Это утверждение привело к созданию различных схем выполнения опытов в стабилометрах. Испытания в приборах трехосного сжатия применяются давно и основные работы по их классификации выполнены в 60–70-е г. ХХ в. [102, 111]. Укрупненная классификация трехосных испытаний дается по трем основным состояниям [102], к которым относят условия насыщения материала водой, консолидации и дренирования. По этим признакам трехосные испытания подразделяются в нормативных документах РФ [16], Евросоюза, Великобритании и США [64, 65, 73, 95, 96]. В более детальной классификации дают условия воздействия нагрузки, развития порового давления, строительства сооружения (табл. 4.5) [111].

Таблица 4.5. Типы трехосных испытаний [111]

Условия	Типы трехосных испытаний
	НН (NUU)	КН (CU)	КД (CD)

Увлажнение	Естественная	Водонасыщенное	Водонасыщенное
	влажность	состояние	состояние

Консолидация	Не консолиди-	Консолидирован-	Консолидирован-
	рованное	ное	ное

Дренирование	Не дренирован-	Не дренированное	Дренированное
	ное
		Быстрое соору-	Длительное
	Окончание		строительство
Строительство		жение нижней
	строительства		или осушение на-
		части насыпи
			сыпи

Приложения	Быстродейст-	Быстродейст-	Длительная на-
	вующая нагруз-
нагрузки		вующая нагрузка	грузка
	ка
Развитие избыточно-	Практически не	Развивается	Не развивается
го порового давления	развивается

162

В Европе и США в конце 60-х, начале 70-х гг. ХХ в. начали широко применяться динамические трехосные испытания грунтов и гранулированных материалов, используемых в дорожном и железнодорожном строительстве [66, 67, 70]. В 70-х и 80-х гг. такие испытания получили широкое признание и проводились специалистами всех континентов.

П. Дж. Грейб и К.Р. Клейтон [85] пришли к выводу о том, что трехосные испытания не подходят для интерпретации напряжений, возникающих в элементах дорожных конструкций. Это мнение связано с тем, что в результате подвижности нагрузки в каждой точке слоя по мере изменения расстояния до нагрузки будет иметь место вращение главных напряжений [85], чего нельзя добиться в приборах трехосного сжатия. Сторонники классических трехосных испытаний парируют этот довод тем, что деформационные и прочностные характеристики материала, установленные при помощи трехосных испытаний, оказываются гораздо точнее, чем вычисленные по эмпирическим формулам, связывающим эти характеристики с каким-либо параметром, определяемым классическими стандартными испытаниями. Так Алан Паррок пишет о том, что значения модулей упругости, установленные при помощи трехосных испытаний, всегда точнее значений, вычисленных по любой из известных эмпирических формул, связывающих этот параметр с калифорнийским числом несущей способно-

сти грунта (CBR) [111].

Следует отметить, что на результаты трехосных испытаний влияет ряд факторов, которые могут приводить к необходимости корректировки. При испытании грунтовых образцов в стабилометре их напряженное деформированное состояние может быть неоднородным [5]. Исследования Г.Г. Болдырева [5], Д. Фроста и К.Т. Янга [81] показывают, что одним из факторов, влияющих на возникновение неоднородного НДС, является трение на гранях образца. Д. Бовард и П. Стьюц [69], А. Прашант, Д. Пеньюмади А. Сачан [113, 115] установили, что уменьшению трения торцов образца о концевики прибора способствует введение смазки, что позволяет добиться более однородного НДС. Принципиально иное мнение высказали Е.В. Меркульев, И.А. Третьяков и Г.Г. Болдырев [37], выполнившие сопоставительные испытания связного грунта при различном состоянии основания и штампа стабилометра. В ходе сопоставительных испытаний было апробировано 4 условия. В первых двух случаях штамп и основание стабилометра оборачивались резиновой оболочкой такой же,

163

как и образец, а поверх оболочки наносился литол или вазелин [37]. В третьем случае испытания были проведены при стандартных граничных условиях, то есть при расположении между образцом и концевиками стабилометра дисков из фторопласта [37]. В последнем на концевиках устанавливалась крупная наждачная бумага, посредством чего было создано так называемое абсолютное трение [37]. В результате установлено, что образцы с концевиками из фторопласта и наждачной бумаги имеют практически одинаковую прочность [37], а вазелин размягчает грунт, примыкающий к концевикам, что приводит к преждевременному разрушению. Е.В. Меркульев, И.А. Третьяков и Г.Г. Болдырев прямо указывают на то, что вазелин в качестве смазки использовать нельзя. Образцы с концевиками, смазанными литолом при 3=200 кПа и 3=600 кПа, имели более высокую прочность по сравнению с гладким контактом, а при 3=400 кПа отмечена диаметрально противоположная картина [37]. При гладком контакте происходило увеличение диаметра образца как в центральной, так и в верхней частях образца [37], причем деформации концентрировались в верхней части образца. Эти выводы свидетельствуют о том, что без тщательного подбора смазывающего материала испытания необходимо производить при стандартном контакте. При таком контакте на концевиках прибора размещены диски из фторопласта, а поправки на их деформирование введены в программу обработки результатов испытаний. Вторым фактором, влияющим на результаты испытаний, является отношение высоты образца к его диаметру. В оценке этого фактора многие авторы высказывают единодушное мнение, в соответствии с которым данное отношение должно варьироваться в пределах 1,5 – 2. При меньшем отношении высоты к диаметру образцы имеют большую прочность, а при большем отношении результаты испытаний практически совпадают [5, 37].

Подводя итог дискуссии по поводу пригодности трехосных испытаний для материалов конструкций, воспринимающих воздействие от подвижных нагрузок, отметим, что все особенности такой нагрузки современные приборы воспроизвести не позволяют, но именно эти испытания моделируют трехосное сжатие, возникающее в дискретных материалах дорожных конструкций. Поэтому для таких материалов трехосные испытания являются наиболее точными.

Именно трехосные испытания необходимо произвести для оценки точности критериев прочности и условий пластичности. При обработке результатов таких испытаний можно сравнить измеренную пре-

164

дельную величину максимального главного напряжения с ее теоретическим аналогом, вычисляемым из условия пластичности. Кроме того, вычисленное предельное значение максимального главного напряжения может быть сопоставлено с измеренной при трехосном сжатии величиной максимального главного напряжения, которой соответствует определенная вертикальная деформация. Это позволяет подобрать критерий, по которому предельные напряжения соответствуют определенной величине деформации. Если в качестве условия пластичности принять уравнение предельного состояния (4.55), то задачей трехосных испытаний является определение параметра d. В этом случае данные нормативных документов о величине сцепления и угле внутреннего трения остаются без изменений, но дополняются значениями третьего параметра грунта.

Другой путь экспериментальных исследований состоит в обосновании предельной величины деформации образца, которое приведет к снижению ее величины по сравнению с регламентируемым стандартом [16] значением 15 %. В этом случае условием пластичности будет уравнение предельного состояния Кулона – Мора, но параметры касательной к кругам предельных напряжений изменятся. Это потребует пересмотра значений сцепления и угла внутреннего трения, регламентируемых документами по расчету дорожных одежд [46, 47].

По нашему мнению, первый путь является более предпочтительным. Его достоинства заключаются в том, что:

1.Предлагается новое условие пластичности, полученное вводом

вуравнение предельного состояния критерия Кулона – Мора третьего параметра d. Варьирование величины этого критерия приводит к изменению предельной поверхности. При d=0 предельная поверхность модифицированного критерия является поверхностью Треска. Радиус круга предельных напряжений такой поверхности определяется величиной сцепления грунта (сцепление Кулона – Мора), которое меньше сцепления Треска, вычисленного по формуле (4.9) (см. табл. 4.4). При увеличении параметра d размеры предельной поверхности увеличиваются, вследствие чего она становится больше шестигранника Треска, имея разные пределы прочности на сжатие и сдвиг, что следует из формул (4.51), (4.52) и рис. 4.5, 4.6. Предельной величины поверхность достигает при d=0,5, в этом случае она совпадает с шестигран-

ником Мора. Известно, что при напряженном состоянии 1> 2= 3 цилиндр Мизиса совпадает с призмой Треска по ребрам сжатия и растяжения или, как еще говорят, на плоскости главных напряжений эл-

165

липс Мизеса проходит по углам сжатия и растяжения шестигранника Треска. Таким образом, эллипс Мизеса расположен между наименьшей и наибольшей предельными поверхностями предлагаемого условия пластичности. Также отметим, что одним из общепринятых недостатков критерия Кулона – Мора является неучет влияния промежуточного главного напряжения на прочность или пластичность материала. При напряженном состоянии 1> 2= 3 условие пластичности Кулона – Мора таким недостатком не обладает. Это следует из анализа критериев Друкера – Прагера, записанных нами для сжатия и растяжения в общем виде (4.25) – (4.27), а также для напряжений

1> 2= 3 (4.28) и (4.29). В последнем случае из (4.28) и (4.29) получен критерий Кулона – Мора для сжатия (4.30) и растяжения (4.31). Поэтому в пространстве главных напряжений конусы Друкера, построенные для сжатия и растяжения, совпадают с ребрами сжатия или растяжения пирамиды Мора. На девиаторной плоскости совпадение одного из предельных кругов Друкера – Прагера с углами сжатия шестигранника Мора показано на рис. 4.2.

2. Существующие данные о величине сцепления и угле внутреннего трения остаются без изменений. База данных о характеристиках сопротивления дискретных материалов и грунтов сдвигу всего лишь дополняется третьим параметром d. Значения этого параметра определены экспериментально таким образом, что модифицированный критерий связан с деформацией образца при трехосных испытаниях.

Из анализа табл. 4.5 следует, что для грунтов рабочего слоя земляного полотна наиболее пригодными являются неконсолидированные недренированные НН испытания. В соответствии с российскими стандартами [16] такие испытания производятся для определения сопротивления недренированному сдвигу, которое вычисляется половиной разрушающего девиатора напряжений, что следует из второго уравнения (4.2). В некотором смысле сопротивление недренированному сдвигу подобно сцеплению Треска, отличаясь от него тем, что при НН испытаниях круги предельных напряжений имеют одинаковый радиус, вследствие чего недренированная прочность для всех кругов одинакова. Сцепление Треска характерно для каждого круга и может быть установлено по данным любых испытаний. При НН трехосном сжатии сцепление Треска и сопротивление недренированному сдвигу совпадают. Для определения параметров предельной прямой Кулона – Мора НН испытания не проводятся. Вследствие этого определение сцепления и угла внутреннего трения выполняют по данным

166

консолидированного недренированного КН или консолидированного дренированного КД испытаний. Из табл. 4.5 следует, что для определения сцепления и угла внутреннего трения грунта в земляном полотне наиболее предпочтительны консолидированные недренированные тесты.

Поэтому возникает необходимость в выполнении испытаний по двум схемам.

Первая группа образцов должна тестироваться по схеме КН испытаний [16], что позволит выполнить определение сцепления и угла внутреннего трения.

Вторую группу образцов необходимо испытать по НН схеме, что дает возможность построить зависимость вертикальной деформации от главных напряжений. Впоследствии появляется возможность определить экспериментальные значения деформации, соответствующие теоретическим предельным значениям максимального главного напряжения, вычисленного по формуле (4.60) при различной величине параметра d.

Изготовление образцов обеих групп выполнено из одного и того же грунта (табл. 4.6).

Таблица 4.6. Показатели физических характеристик грунта [17]

Характеристики


плотности, г/см3						пористости, д.е.							влажности								пластичности
s			d			n				е			Sr		WL, %		Wp, %				Ip, %	IL
2,68		1,74		2,05		0,35			0,54			0,88		21,70				14,50			7,20	0,46
						Гранулометрический состав
Гравий					Песчаный								Пылеватый						Глинистый			Итого
>5	5-2		2-1	1-		0,5-	0,25-				0,10-		0,05-			0,01-				0,005
>5	5-2		2-1	0,5		0,25		0,10			0,05		0,01			0,005				0,005		100
0	0		4,68	0,13		9,93		43,18			10,67		13,38			6,17				11,86		100
0	0		4,68	0,13		9,93		43,18			10,67		13,38			6,17				11,86
0					68,59								19,55							11,86
Разновидность грунта по ГОСТ 25100													Суглинок легкий песчанистый

Примечание. s, d и – плотность частиц грунта, сухого грунта и грунта соответственно; n и e – пористость и коэффициент пористости; WL и Wp – влажности на границах текучести и раскатывания; Sr – коэффициент водонасыщения; Iр и IL – число пластичности и показатель текучести.

Учитывая необходимость такого сценария испытаний, нами8 из одного и того же грунта выполнялось изготовление 9 образцов, имеющих

8 Испытания образцов выполнены совместно с Г.В. Долгих [17].

167

одинаковую влажность и плотность. Для изготовления образцов использовалась навеска сухого грунта массой 10 кг. Грунт увлажнялся до влажности, близкой оптимальной, и формовался при помощи прибора для стандартного уплотнения (ПСУ). Методика изготовления образца такая же, как при определении максимальной плотности, регламентируемой ГОСТ 22733-2002 [15]. Из одной навески изготавливалось 3 образца высотой127,4 0,2 мми диаметром100+0,3 мм (рис.4.8).

Рис. 4.8. Образец, изготовленный при	Рис. 4.9. Размещение образца в при-
помощи ПСУ	способлении для отбора проб

Изготовленный при помощи ПСУ образец помещался в приспособление для отбора проб (рис. 4.9). При помощи этого приспособления и режущих колец, которыми укомплектован измерительный вычислительный комплекс АСиС-1, из верхней части пробы отбиралось три малых образцавысотой 76мми диаметром38 мм (рис.4.10 и4.11).

Рис. 4.10. Кольца, врезанные в образец,	Рис. 4.11. Общий вид колец, взятых из
изготовленный в ПСУ	большого образца

168

Далее образцы взвешивались, что при известной массе и объеме колец позволяло определить плотность грунта. После взвешивания при помощи приспособления для извлечения образцов они выдавливались из колец (рис. 4.12) и осматривались на наличие возможных дефектов. Из каждой группы, насчитывающей 9 образцов, отбирались 6 наилучших проб, не имеющих дефектов поверхности, для их дальнейших испытаний (рис. 4.13).

Рис. 4.12. Извлечение образца из кольца	Рис. 4.13. Общий вид образца, подго-
при помощи выталкивателя	товленного к испытанию

Выбранные образцы делились на две группы. Одна группа из 3 образцов испытывалась по схеме КН испытаний, а вторая группа из оставшихся 3 образцов испытывалась по НН схеме. Обе схемы испытаний реализуются в камере трехосного сжатия типа В, которой укомплектован измерительный вычислительный комплекс АСИС-1 (рис. 4.14).

Для предотвращения высыхания образцов они сразу же после извлечения из колец пробоотборников оборачивались пищевой полиэтиленовой пленкой, затем уклады-

Рис.4.14. Измерительный вычислительный комплекс АСИС-1 с камерой трехосного сжатия типа В

169

вались в полиэтиленовый пакет и помещались на хранение в эксикатор. Таким образом, в течение испытания одного образца остальные в полиэтилене находились в эксикаторе. После испытания каждого образца из его верхней средней и нижней частей отбиралось три пробы и методом высушивания до постоянной массы производилось определение влажности. После испытаний всех 6 образцов определялась средняя влажность и среднее значение плотности сухого грунта.

КН и НН испытания выполнялись в соответствии с нормативной методикой ГОСТ 12248-2010 [16].

Рис. 4.15. НН испытание суглинка легкого в стабилометре на АСИС-1

Рис. 4.16. Визуализация трехосных испытаний (разрушение произошло срезом)

Любое из испытаний, выполняемых при помощи измерительного вычислительного комплекса АСИС-1 (рис. 4.15), ви-

зуализируется на компьютере в реальном времени (рис. 4.16). По данным НН испытаний, выполнено построение зависимости относительной осевой деформации от главных напряжений. В этом случае наглядно видно, какой величине вертикальной деформации соответствуют главные напряжения. Если за основу взять выводы японских специалистов, что зарождение и развитие в образце поверхностей скольжения происходит при деформации, варьирующейся в диапазоне от 8 до 12 % [91, 92, 108], то появляет-

ся возможность определить диапазон варьирования максимального глав-

170

ного напряжения, соответствующий указанным деформациям. В этом случае становится возможным подбор параметра d, введенного нами для модификации условия Кулона – Мора (4.55).

Из анализа экспериментальных данных следует, что отказ образца наступал по одной из двух схем. Г.Г. Болдырев классифицирует эти схемы как разрушение срезом (рис. 4.17) и бочкообразное разрушение (рис. 4.18).

Рис. 4.17. Разрушение образца срезом

Рис. 4.18. Бочкообразное разрушение

По сути, разрушение срезом происходит за счет распространения трещины по одной из площадок скольжения. Так как причиной этого разрушения является трещина, то его можно назвать хрупким, или еще точнее, квазихрупким9 разрушением по площадке сдвига. В последний термин вкладываем то, что при развитии площадок скольжения вдоль них локализуются пластические деформации, приводящие к постепенному росту поврежденности образца с последующим ростом трещины по одной из поверхностей сдвига. Критерием бочкообразного разрушения является деформирование образца на предельную величину. В этом случае разрушение можно было бы классифицировать как пластическое, но отказ образца по деформации не гарантирует отсутствие разрушения сдвигом при больших предельных деформациях. Например, деформирование образца на величину 15 %, регламентируемую стандартами РФ как предельное значение, не означает, что этот образец не разрушится срезом при его деформировании на 18 %, что меньше деформации 20 %, принимаемой за предельное

9 В приставку «квази» автор вкладывает смысл латинского слова quasi, дословно означающего ,,якобы’’ или как ,,будто’’. Под этой приставкой также можно понимать: мнимый, ненастоящий, почти, близко.

171

значение в стандартах США. Поэтому бочкообразное разрушение целесообразно называть квазипластическим.

Результаты КН испытаний в камере трехосного сжатия и данные о показателях физических свойств грунта в каждом образце приведены в табл. 4.7.

Таблица 4.7. Показатели физических свойств суглинка легкого и результаты

определения параметров предельной прямой Кулона – Мора

№ об-	Показатели физических свойств,					Показатели механических
разца	установленные по ГОСТ 5180-84					свойств и 3	при КН испытани-
			[13]				ях
	W, %	Wт, %		W/ Wт	d, т/м3	3, кПа	с, кПа	, град
1	22	3		4	5	6	7	8
1 (КН)	9,87	19,7		0,50	1,83	50	18	22
2 (КН)	9,87	19,7		0,50	1,82	100	18	22
3 (КН)	9,87	19,7		0,50	1,83	125
4 (КН)	11,02	19,7		0,56	1,82	100	24	20
5 (КН)	11,05	19,7		0,56	1,80	125	24	20
6 (КН)	11,17	19,7		0,57	1,81	175
7 (КН)	10,95	19,7		0,56	1,81	100	22	28
8 (КН)	10,95	19,7		0,56	1,81	150	22	28
9 (КН)	10,95	19,7		0,56	1,81	200
10 (КН)	10,91	19,7		0,55	1,83	100	24	27
11 (КН)	10,91	19,7		0,55	1,83	150	24	27
12 (КН)	10,91	19,7		0,55	1,83	200
13 (КН)	10,46	19,7		0,53	1,85	100	15	25
14 (КН)	10,46	19,7		0,53	1,85	150	15	25
15 (КН)	10,46	19,7		0,53	1,85	200
16 (КН)	11,72	19,7		0,59	1,84	100	15	10
17 (КН)	11,09	19,7		0,56	1,86	150	15	10
18 (КН)	11,54	19,7		0,59	1,85	200
19 (КН)	11,21	19,7		0,57	1,84	100	15	10
20 (КН)	11,65	19,7		0,59	1,85	150	15	10
21 (КН)	11,01	19,7		0,56	1,81	200
22 (КН)	10,66	19,7		0,54	1,84	50	19	26
23 (КН)	10,61	19,7		0,54	1,83	100	19	26
24 (КН)	10,59	19,7		0,54	1,85	150
25 (КН)	13,22	19,7		0,67	1,84	75	30	20
26 (КН)	13,02	19,7		0,66	1,83	125	30	20
27 (КН)	13,42	19,7		0,68	1,85	175
28 (КН)	10,24	19,7		0,52	1,84	200	22	19
29 (КН)	10,26	19,7		0,52	1,83	250	22	19
30 (КН)	10,40	19,7		0,53	1,85	300

172

Окончание табл. 4.7

1	2	3	4	5	6	7	8
31 (КН)	13,50	19,7	0,69	1,84	225	17	17
32 (КН)	13,60	19,7	0,69	1,85	275	17	17
33 (КН)	13,12	19,7	0,67	1,84	325
34 (КН)	18,02	30,03	0,60	1,73	150	18	18
35 (КН)	18,02	30,03	0,60	1,71	200	18	18
36 (КН)	18,02	30,03	0,60	1,70	250

Примечание. Оптимальная влажность грунта образцов № 1–33 составляет 12,5 %, а максимальная стандартная плотность – 1,86 т/м3. Образцы с номерами 34, 35, 36 отобраны с дороги Петровка-Калиновка ПК 15-80. Максимальная стандартная плотность грунта образцов № 34–36 составляет 1,75 т/м3.

Трехосные испытания по НН схеме выполнялись с одним, но важным отступлением от экспериментальной методики, регламентируемой [16]. Это изменение касалось времени между приложениями ступеней нагрузки. В соответствии с требованиями стандарта [16, п. 5.3.4.2] интервал между ступенями девиаторной нагрузки назначают в пределах от 15 с до 1 мин (большие значения принимают для глинистых грунтов твердой и полутвердой консистенции). Соблюдение этого требования необходимо для того, чтобы предельные круги Мора, построенные в эффективных напряжениях, имели одинаковый радиус при различных значениях удерживающего напряжения 3. По кругам предельных эффективных напряжений определяется сопротивление недренированному сдвигу cu. При выполнении трехосных НН испытаний нами ставилась цель определить зависимость осевой (продольной) деформации образца от главных напряжений в условиях, максимально приближенных к воздействию кратковременной нагрузки. Поэтому интервал времени между ступенями нагрузки мы уменьшили от 1 мин до 1 с. Это наименьший промежуток времени, который можно задать в программе испытаний, прилагаемой к комплексу АСИС-1. После выполнения испытаний было обнаружено, что предельные значения девиаторов при разных значениях 3 не одинаковы. Это нас озадачило, вследствие чего некоторые испытания нами были продублированы, но с интервалом времени ступени девиатора 1 мин. Во втором случае круги предельных напряжений имели одинаковый радиус. Поэтому полученные и иллюстрируемые нами ниже данные нельзя применить к определению недренированной прочности грунта. Эти данные предназначены для определения зависимости деформации образцов от главных напряжений при продолжительности девиаторной нагрузки 1 с. Из этих данных можно определить пара-

173

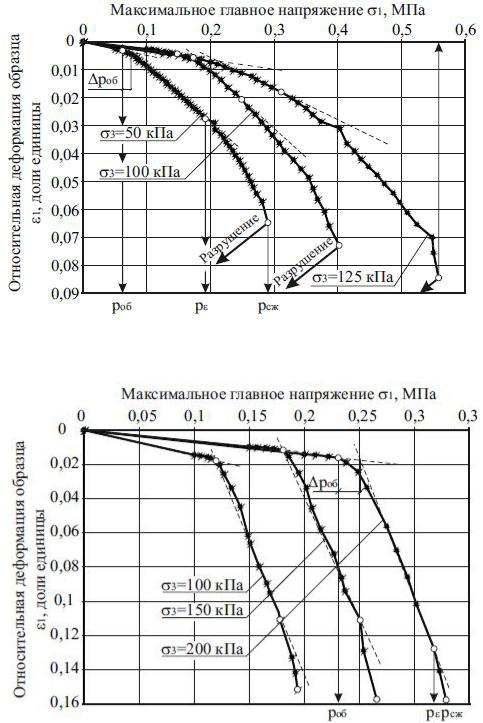
метры деформируемости грунта при продолжительности девиаторной нагрузки 1 с. В выполненных нами трехосных НН испытаниях образцы испытывали два вида разрушения: квазихрупкое по площадке сдвига (рис. 4.19) и квазипластическое при деформировании на 15 % (рис. 4.20).

Рис. 4.19. Зависимость осевой деформации 1 образцов №1-3 от величины напряжений 1 и 3 (квазихрупкое разрушение)

Рис. 4.20. Зависимость осевой деформации 1 образцов №16-18 от величины напряжений 1 и 3 (квазипластическое разрушение)

174

При квазихрупком разрушении предельная деформация 1пр, при которой происходил сдвиг, варьировалась в диапазоне от 6 до15 % (рис. 4.19). Величина предельной деформации при квазихрупком разрушении зависит от величины удерживающего напряжения 3 и свойств грунта.

Выполнив анализ результатов испытаний, мы пришли к выводу, что при квазихрупком или квазипластическом разрушении зависимость деформации от главного напряжения 1 является нелинейной, но такую зависимость можно представить приближением, состоящим из трех участков. Первые два участка являются кусочно-линейной зависимостью, а третий представляет собой нелинейную функцию (рис. 4.19 и 4.20).

Предельная деформация для первого прямолинейного участка варьируется в пределах от 0,3 до 2 %. Большие значения предельных деформаций для этого участка характерны для квазипластического разрушения (см. рис. 4.20). Известно, что такие относительно малые деформации носят преимущественно обратимый характер. Поэтому абсциссу точки, ограничивающей первый участок, можно считать приближенным пределом обратимости деформации роб (приближенным пределом структурной прочности рстр).

Отметим, что различные сопротивления материала (пределы пропорциональности, упругости, текучести и прочности) принято классифицировать на абсолютные, условные и приближенные [45]. Под абсолютным пределом понимают величину напряжения, при которой имеет место некий физический факт, заключающийся в кардинальном изменении характера деформирования, например, начало текучести. Причем абсолютный предел не зависит от того, существует ли прибор, способный его обнаружить или нет [45]. Как правило, из всех абсолютных пределов экспериментально можно определить только предел прочности, при котором измеряется нагрузка, соответствующая разрушению образца. Для других пределов сопротивления материала используют понятия условного или приближенного предела. Величина условного предела определяется при определенном принятом условии. Например, условный предел текучести металлов определяют по величине напряжения, которому соответствует пластическая деформация 0,2 % [45]. Предел прочности Rс является условным при квазипластическом разрушении, то есть тогда, когда отказ образца принят по величине его осевой деформации. Приближенные пределы удаётся определить непосредственно из опыта [45].

175

Поэтому определяемый нами предел обратимости деформации является приближенным пределом. Точность его определения зависит от углов наклона двух пересекающихся прямых к осям абсцисс и ординат (см. рис. 4.19 и 4.20). В связи с этим экспериментальное значение предела обратимости может не совпадать с абсциссой точки перелома двух прямых отрезков (см. рис. 4.19 и 4.20 при 3=200 кПа). Разница между экспериментальным и приближенным значением предела обратимости деформаций не превышает 20 %. Наличие такой разницы свидетельствует о том, что при приближении таких нелинейных зависимостей кусочно-линейными количество прямолинейных участков должно быть больше двух. В этом случае экспериментальные значения координат точки, ограничивающей первый линейный участок, будут совпадать с координатами точки перелома первого и второго участков кусочно-линейной зависимости. Это замечание автора имеет существенное значение при поиске приближающих ку- сочно-линейных зависимостей деформации от главных напряжений. Для определения приближенного значения предела обратимости это замечание принципиального значения не имеет потому, что приближенное значение этого предела принимается равным абсциссе экспериментальной точки, ограничивающей первый прямой отрезок. Вторая и третья точки приближающей зависимости имеют точно такие же координаты, как и точки на экспериментальном графике. Абсциссу второй точки, ограничивающей второй прямой отрезок, назовем приближенным пределом линейности деформаций р . Экспериментальные значения всех трех пределов, установленных автором совместно с Г.В. Долгих и А.Л. Калининым, приведены в табл. 4.8.

	Таблица	4.8.	Экспериментальные значения				пределов роб,		р . Rс
исоответствующие им осевые деформации [17]
№ об-		роб,	1об, %	р , кПа	1 , %	Rс,	1с, %	с, кПа	,
разца		кПа				кПа			град
	1	2	3	4	5	6	7	8	9
1	(НН)	62	0,32	192	2,75	290	6,57	18	22
2	(НН)	148	0,43	249	2,07	402	7,29	18	22
3	(НН)	173	0,53	311	1,80	558	8,45
4	(НН)	129	0,42	232	7,77	304	15,42	24	20
5	(НН)	172	0,47	301	8,12	375	15,84	24	20
6	(НН)	208	1,25	338	8,36	417	15,32
7	(НН)	110	0,58	321	8,50	384	15,18	22	28
8	(НН)	171	1,25	480	11,13	543	15,66	22	28
9	(НН)	230	1,30	541	12,55	581	15,83

176

Окончание табл. 4.8

1	2	3	4	5	6	7	8	9
10 (НН)	126	0,76	321	8,5	378	15,18	24	27
11 (НН)	172	0,91	459	10,09	539	15,17	24	27
12 (НН)	241	1,06	552	13,68	570	15,25
13 (НН)	131	1,14	353	7,84	451	13,42	15	25
14 (НН)	195	1,07	382	7,76	468	12,87	15	25
15 (НН)	238	0,66	460	7,53	522	10,87
16 (НН)	120	1,79	178	11,08	194	15,16	15	10
17 (НН)	180	1,16	251	11,09	266	15,74	15	10
18 (НН)	231	1,62	318	12,76	329	15,78
19 (НН)	120	1,83	193	11,79	206	15,13	15	10
20 (НН)	180	1,68	248	11,13	270	15,25	15	10
21 (НН)	239	1,35	299	11,07	327	15,63
22 (НН)	61	0,33	204	10,66	237	14,60	20	27
23 (НН)	126	0,28	254	6,68	347	10,80	20	27
24 (НН)	177	0,10	375	6,28	488	9,80
25 (НН)	86	0,45	249	11,83	286	15,00	30	20
26 (НН)	139	0,65	329	11,86	360	15,10	30	20
27 (НН)	193	0,60	361	13,16	392	15,11
28 (НН)	216	0,41	462	7,68	550	10,60	22	19
29 (НН)	272	0,53	554	7,31	608	10,30	22	19
30 (НН)	319	0,65	528	12,53	582	15,06
31 (НН)	231	0,82	400	12,75	424	15,10	15	12
32 (НН)	305	0,80	466	12,38	505	15,10	15	12
33 (НН)	355	0,83	506	12,53	536	15,10
34 (НН)	194	1,39	335	8,71	379	15,37	18	18
35 (НН)	264	0,64	428	10,42	466	15,03	18	18
36 (НН)	310	1,43	482	9,14	554	15,3

Анализируя данные табл. 4.8, автор совместно с Г.В. Долгих обратили внимание на то, что при квазипластическом разрушении приближенный предел линейности деформаций соответствует диапазону деформаций 7 – 13 %. Это согласуется с данными японских специалистов о формировании площадок скольжения при осевой деформации, варьирующейся в диапазоне 8 – 12 % [91, 92, 108]. Поэтому нами ставилась цель подбора условия пластичности, по которому предельная величина максимального главного напряжения наилучшим образом совпадает с пределом линейности деформации. Основное внимание уделялось критериям Кулона – Мора (4.7) или (4.43) и Г.К. Арнольда (4.44). Расчет предельных значений максимального главного напряжения критерия Кулона – Мора выполнен по тождественным друг

177

другу формулам (4.36) и (4.56). Определение предельных значений максимального главного напряжения критерия Г.К. Арнольда выполнено по формуле

	2 с	1	sin		.	(4.63)

1пр	1		sin	3

В табл. 4.9 приведены входные параметры и результаты расчета предельных значений максимальных главных напряжений.

Таблица 4.9. Сопоставление экспериментальных и теоретических

пределов линейности деформаций и прочности при трехосном сжатии

	Входные параметры			Предельные максимальные главные на-
№	Входные параметры				пряжения, кПа
№					пряжения, кПа
образца	с, кПа	, о	3, кПа	Расчет по формулам			Эксперимент
образца	с, кПа	, о	3, кПа	(4.36) и (4.56)		(4.63)	р	Rс
1	2	3	4	5		6	7	8
1 (НН)	18	22	50	163		146	192	290
2 (НН)	18	22	100	273		256	249	402
3 (НН)			125	328		311	311	558
4 (НН)	24	20	100	273		252	232	304
5 (НН)	24	20	125	324		303	301	375
6 (НН)			175	425		405	338	417
7 (НН)	22	28	100	350		321	321	384
8 (НН)	22	28	150	489		459	480	543
9 (НН)			200	627		598	541	581
10 (НН)	24	27	100	345		314	321	378
11 (НН)	24	27	150	478		447	459	539
12 (НН)			200	611		581	552	570
13 (НН)	15	25	100	293		276	353	451
14 (НН)	15	25	150	417		400	382	468
15 (НН)			200	540		523	460	522
16 (НН)	15	10	100	178		172	178	194
17 (НН)	15	10	150	249		243	251	266
18 (НН)			200	320		314	318	329
19 (НН)	15	10	100	178		172	193	206
20 (НН)	15	10	150	249		243	248	270
21 (НН)			200	320		314	299	327
22 (НН)	20	27	50	198		173	204	237
23 (НН)	20	27	100	332		306	254	347
24 (НН)			150	465		439	375	488
25 (НН)	30	20	75	239		213	249	286
26 (НН)	30	20	125	341		315	329	360
27 (НН)			175	443		417	361	392

178

Окончание табл. 4.9

1	2	3	4	5	6	7	8
28 (НН)	22	19	200	455	437	462	550
29 (НН)	22	19	250	553	535	554	608
30 (НН)			300	651	634	528	582
31 (НН)	15	12	225	380	373	400	424
32 (НН)	15	12	275	456	449	466	505
33 (НН)			325	533	526	506	536
34 (НН)	18	18	150	334	320	335	379
35 (НН)	18	18	200	428	415	428	466
36 (НН)			250	523	510	482	554

Из данных табл. 4.9 следует, что предельная величина максимального главного напряжения, вычисленного по формуле (4.63), ближе к пределу линейности деформаций. Предельное максимальное напряжение условия Кулона – Мора наоборот ближе к пределу прочности на трехосное сжатие. Сопоставление простых ошибок, выраженных в процентах между результатами расчета и данными эксперимента, выполнил Г.В. Долгих и привел их в своей диссертации [17].

Для определения параметра d, входящего в рекомендуемое условие (4.55), необходимо рассматривать величину главных напряжений, при которых формируются и развиваются площадки скольжения. Из анализа данных табл. 4.9 следует, что некоторые образцы разрушились при деформациях меньше 8 и тем более 12 %. Это означает, что в этих образцах площадки скольжения появились и развивались при меньшей осевой деформации, чем зафиксированные в опытах японских коллег [91, 92, 108]. Поэтому нами сделан вывод, что наряду с характеристиками моментов начала и окончания формирования площадок скольжения по величине осевой деформации следует рассматривать характеристики, определяемые отношением этих деформаций к предельной деформации отказа образца. Если деформацию, соответствующую началу формирования площадок сдвига 1н=8 %, разделить на предельную деформацию 1с=15 %, то получим 1н/ 1с 0,5. Точно так же разделив на величину 1с=15 % деформацию, соответствующую окончанию формирования площадок скольжения 1к=12 %, получим 1н/ 1с=0,8.

В табл. 4.10 приведены характеристики условий работы грунта, обусловленные локализацией пластических деформаций вдоль площадок сдвига, которые приводят к началу формирования площадок скольжения и их дальнейшему развитию.

179

Таблица 4.10. Условия работы образца глинистого грунта в различных

диапазонах варьирования осевой деформации при трехосном сжатии

Варьирование де-		1	0,5	0,5	1	0,8		1		0,8
формации 1, доли

		1с			1с			1с
от предельной 1с

	Преимущественно			Сдвиг, локализа-			Преимущест-
Условия работы об-	уплотнение, лока-			ция пластических			венно			пластиче-
	лизация		пластиче-	деформаций			ское		течение с
разца	ских деформаций			вдоль площадок			последующим

	отсутствует			скольжения			отказом

В табл. 4.11 приведены отношения измеренных при трехосном сжатии деформаций 1об/ 1с и 1 / 1с (см. табл. 4.8).

Таблица 4.11. Отношения деформаций 1об/ 1с и 1 / 1с

№	1об,	1 ,	1с,	1об	1с	1	1с
образца	%	%	%	Величина	Интервал	Величина	Интервал
1	2	3	4	5	6	7	8
1 (НН)	0,32	2,75	6,57	0,12	<0,5	0,42	Менее 0,5
2 (НН)	0,43	2,07	7,29	0,21	<0,5	0,28	Менее 0,5
3 (НН)	0,53	1,80	8,45	0,29	<0,5	0,21	Менее 0,5
4 (НН)	0,42	7,77	15,42	0,06	<0,5	0,50	От 0,5 до 0,8
5 (НН)	0,47	8,12	15,84	0,06	<0,5	0,51	От 0,5 до 0,8
6 (НН)	1,25	8,36	15,32	0,15	<0,5	0,55	От 0,5 до 0,8
7 (НН)	0,58	8,50	15,18	0,07	<0,5	0,56	От 0,5 до 0,8
8 (НН)	1,25	11,13	15,66	0,11	<0,5	0,71	От 0,5 до 0,8
9 (НН)	1,30	12,55	15,83	0,10	<0,5	0,79	От 0,5 до 0,8
10 (НН)	0,76	8,5	15,18	0,09	<0,5	0,56	От 0,5 до 0,8
11 (НН)	0,91	10,09	15,17	0,09	<0,5	0,67	От 0,5 до 0,8
12 (НН)	1,06	13,68	15,25	0,08	<0,5	0,90	Более 0,8
13 (НН)	1,14	7,84	13,42	0,15	<0,5	0,58	От 0,5 до 0,8
14 (НН)	1,07	7,76	12,87	0,14	<0,5	0,60	От 0,5 до 0,8
15 (НН)	0,66	7,53	10,87	0,09	<0,5	0,69	От 0,5 до 0,8
16 (НН)	1,79	11,08	15,16	0,16	<0,5	0,73	От 0,5 до 0,8
17 (НН)	1,16	11,09	15,74	0,10	<0,5	0,70	От 0,5 до 0,8
18 (НН)	1,62	12,76	15,78	0,13	<0,5	0,81	Более 0,8
19 (НН)	1,83	11,79	15,13	0,16	<0,5	0,78	От 0,5 до 0,8
20 (НН)	1,68	11,13	15,25	0,15	<0,5	0,73	От 0,5 до 0,8
21 (НН)	1,35	11,07	15,63	0,12	<0,5	0,71	От 0,5 до 0,8
22 (НН)	0,33	10,66	14,60	0,03	<0,5	0,73	От 0,5 до 0,8
23 (НН)	0,28	6,68	10,80	0,04	<0,5	0,62	От 0,5 до 0,8
24 (НН)	0,10	6,28	9,80	0,02	<0,5	0,64	От 0,5 до 0,8
25 (НН)	0,45	11,83	15,00	0,04	<0,5	0,79	От 0,5 до 0,8

180

Окончание табл. 4.11

1	2	3	4	5	6	7	8
26 (НН)	0,65	11,86	15,10	0,05	<0,5	0,79	От 0,5 до 0,8
27 (НН)	0,60	13,16	15,11	0,05	<0,5	0,87	Более 0,8
28 (НН)	0,41	7,68	10,60	0,05	<0,5	0,72	От 0,5 до 0,8
29 (НН)	0,53	7,31	10,30	0,07	<0,5	0,71	От 0,5 до 0,8
30 (НН)	0,65	12,53	15,06	0,05	<0,5	0,83	Более 0,8
31 (НН)	0,82	12,75	15,10	0,06	<0,5	0,84	Более 0,8
32 (НН)	0,80	12,38	15,10	0,06	<0,5	0,82	Более 0,8
33 (НН)	0,83	12,53	15,10	0,07	<0,5	0,83	Более 0,8
34 (НН)	1,39	8,71	15,37	0,16	<0,5	0,57	От 0,5 до 0,8
35 (НН)	0,64	10,42	15,03	0,06	<0,5	0,69	От 0,5 до 0,8
36 (НН)	1,43	9,14	15,3	0,16	<0,5	0,53	От 0,5 до 0,8

Из анализа табл. 4.11 следует, что отношение деформации образца, ограничивающей второй линейный отрезок 1 , к предельной величине 1с в 26 случаях попадает в интервал от 0,5 до 0,8. В трех случаях это отношение меньше 0,5, а в семи опытах больше 0,8. Характер деформирования образцов № 1–3 резко отличается от зависимости деформаций от напряжений других образцов. Поэтому результаты испытаний этих трех образцов трудно применить для определения параметров d уравнения (4.55). Для оставшихся образцов можно определить экспериментальные значения максимальных главных напряжений, соответствующие различным деформациям. При этом важно, чтобы экспериментальные зависимости деформаций от напряжений следовали классической зависимости. В соответствии с общепринятыми представлениями при увеличении удерживающего напряжения 3, но при одной и той же величине максимального главного напряжения 1 осевая деформация 1 уменьшается. Следовательно, чтобы деформировать грунт на одну и ту же величину, необходимо увеличение напряжения 1 при увеличении удерживающего напряжения 3. Из анализа данных Г.В. Долгих следует, что получить классическую картину деформирования грунта удалось не во всех опытах. Кроме того, предельное максимальное главное напряжение по критерию Кулона – Мора должно незначительно отличаться от экспериментального значения, при котором произошел отказ образца. В идеальном случае эти значения должны совпадать. Это условие имеет место не во всех опытах. При неоднородном деформировании образца может наступать преждевременный отказ, вследствие чего экспериментальные предельные значения будут ниже значений, кото-

181

рые были бы достигнуты при однородном деформировании. То есть предельный девиатор имеет меньшее значение по сравнению с величиной, которая достигается при однородном деформировании. Так как сцепление и угол внутреннего трения являются некоторым осреднением параметров сопротивления сдвига по трем кругам предельных напряжений, то предельные напряжения по критерию Кулона – Мора могут существенно отличаться от предельных экспериментальных значений. Оба описанных нами фактора свидетельствуют о том, что некоторые из испытаний, выполненных Г.В. Долгих, не получились. Поэтому результаты таких испытаний из выборки необходимо исключить. Исключив результаты испытаний образцов № 1–3 и № 13, в табл. 4.12 приведены результаты КН и НН испытаний, включающие экспериментальные значения максимальных главных напряжений, соответствующие различным отношениям деформаций 1/ 1с.

Таблица 4.12.		Экспериментальные отношения				деформаций			1/ 1с
и соответствующие им значения напряжений 1
№	Показатели фи-		Показатели сопротивления			Экспериментальные
образца	зических		сдвигу и 3 по данным КН			значения 1			при
	свойств			испытаний			1/ 1с
	W/ Wт	kу	3, кПа	с, кПа	, град	0,5	0,6	0,7		0,8
1	2	3	4	5	6	7	8	9		10
28 (НН)	0,523	0,99	200	22	19	381	417	453		475
29 (НН)	0,523	0,99	250	22	19	464	507	550		569
30 (НН)			300			440	467	493		520
14 (НН)	0,53	0,995	150	15	25	345	381	406		434
15 (НН)	0,53	0,995	200	15	25	392	427	461		485
15 (НН)			200			392	427	461		485
22 (НН)	0,54	0,99	50	19	26	157	178	198		215
23 (НН)	0,54	0,99	100	19	26	228	250	264		276
24 (НН)			150			331	362	388		406
10 (НН)	0,55	0,98	100	24	27	298	326	354		370
11 (НН)	0,55	0,98	150	24	27	381	428	465		492
12 (НН)			200			403	440	478		516
7 (НН)	0,56	0,973	100	22	28	297	332	355		371
8 (НН)	0,56	0,973	150	22	28	377	426	475		507
9 (НН)			200			413	457	500		544
4 (НН)	0,563	0,373	100	24	20	231	252	272		291
5 (НН)	0,563	0,373	125	24	20	298	323	345		365
6 (НН)			175			325	350	371		388
19 (НН)	0,573	0,986	100	15	10	162	173	184		193
20 (НН)	0,573	0,986	150	15	10	223	234	245		254
21 (НН)			200			279	289	298		306

182

Окончание табл. 4.12

1	2	3	4	5	6	7	8	9	10
16 (НН)	0,58	0,995	100	15	10	156	166	175	181
17 (НН)	0,58	0,995	150	15	10	228	239	250	258
18 (НН)			200			280	292	305	317
34 (НН)	0,6	0,98	150	18	18	315	340	356	367
35 (НН)	0,6	0,98	200	18	18	379	404	430	441
36 (НН)			250			449	483	507	527
25 (НН)	0,67	0,99	75	30	20	187	208	230	246
26 (НН)	0,67	0,99	125	30	20	256	282	307	329
27 (НН)			175			286	306	326	347
31 (НН)	0,683	0,99	225	17	17	326	348	369	391
32 (НН)	0,683	0,99	275	17	17	399	420	441	462
33 (НН)			325			442	461	481	500

Экспериментальные значения напряжений 1 при заданных удерживающих напряжениях 3 и параметрах сопротивления сдвигу позволяют для каждой группы образцов подобрать величину параметра d (табл. 4.13).

Таблица 4.13. Значения параметра d для условия пластичности (4.55)

№	Отношение	Параметр d	Величина максимального глав-		Ошиб-
образца	деформа-	для условия	ного напряжения, кПа		ка, %
образца	ций 1/ 1с	(4.55)	По формуле (4.60)	Эксперимент	ка, %
1	2	3	4	5	6
	0,5	0,30	354	381	7,1
28 (НН)	0,6	0,35	377	417	9,7
28 (НН)	0,7	0,40	401	453	11,5
	0,7	0,40	401	453	11,5
	0,8	0,45	427	475	10,1
	0,5	0,30	429	464	7,6
29 (НН)	0,6	0,35	457	507	9,9
29 (НН)	0,7	0,40	487	550	11,5
	0,7	0,40	487	550	11,5
	0,8	0,45	519	569	8,8
	0,5	0,30	504	440	-14,5
30 (НН)	0,6	0,35	537	467	-15,0
30 (НН)	0,7	0,40	573	493	-16,2
	0,7	0,40	573	493	-16,2
	0,8	0,45	611	520	-17,5
	0,5	0,35	323	345	6,3
14 (НН)	0,6	0,40	352	381	7,7
14 (НН)	0,7	0,44	376	406	7,3
	0,7	0,44	376	406	7,3
	0,8	0,48	403	434	7,2
	0,5	0,35	417	392	-6,4
15 (НН)	0,6	0,40	454	427	-6,4
15 (НН)	0,7	0,44	487	461	-5,6
	0,7	0,44	487	461	-5,6
	0,8	0,48	522	485	-7,5

183

Продолжение табл. 4.13

1	2	3	4	5	6
	0,5	0,35	149	157	4,8
22 (НН)	0,6	0,40	161	178	9,3
22 (НН)	0,7	0,45	175	198	11,8
	0,7	0,45	175	198	11,8
	0,8	0,49	186	215	13,5
	0,5	0,35	246	228	-7,9
23 (НН)	0,6	0,40	268	250	-7,0
23 (НН)	0,7	0,45	291	264	-10,3
	0,7	0,45	291	264	-10,3
	0,8	0,49	312	276	-12,9
	0,5	0,35	343	331	-1,7
24 (НН)	0,6	0,40	374	362	-3,5
24 (НН)	0,7	0,45	408	388	-5,1
	0,7	0,45	408	388	-5,1
	0,8	0,49	437	406	-7,7
	0,5	0,35	343	298	-3,5
10 (НН)	0,6	0,40	374	326	-3,2
10 (НН)	0,7	0,45	408	354	-5,1
	0,7	0,45	408	354	-5,1
	0,8	0,49	437	370	-7,7
	0,5	0,35	266	381	10,7
11 (НН)	0,6	0,40	295	428	9,5
11 (НН)	0,7	0,45	316	465	10,7
	0,7	0,45	316	465	10,7
	0,8	0,49	327	492	11,6
	0,5	0,35	365	403	4,1
12 (НН)	0,6	0,40	407	440	5,0
12 (НН)	0,7	0,45	437	478	6,1
	0,7	0,45	437	478	6,1
	0,8	0,49	453	516	8,0
	0,5	0,35	267	297	10,1
7 (НН)	0,6	0,40	292	332	12,0
7 (НН)	0,7	0,45	320	355	9,9
	0,7	0,45	320	355	9,9
	0,8	0,47	332	371	10,6
	0,5	0,35	369	377	2,1
8 (НН)	0,6	0,40	405	426	4,9
8 (НН)	0,7	0,45	445	475	6,4
	0,7	0,45	445	475	6,4
	0,8	0,47	462	507	8,9
	0,5	0,35	471	413	-14,0
9 (НН)	0,6	0,40	518	457	-13,3
9 (НН)	0,7	0,45	570	500	-14,0
	0,7	0,45	570	500	-14,0
	0,8	0,47	592	544	-8,8
	0,5	0,35	226	231	2,0
4 (НН)	0,6	0,42	247	252	2,1
4 (НН)	0,7	0,47	263	272	3,5
	0,7	0,47	263	272	3,5
	0,8	0,49	269	291	7,5
5 (НН)	0,5	0,35	267	298	10,2
5 (НН)	0,6	0,42	292	323	9,5
	0,6	0,42	292	323	9,5

184

Продолжение табл. 4.13

1	2	3	4	5	6
5 (НН)	0,7	0,47	311	345	9,7
5 (НН)	0,8	0,49	319	365	12,5
	0,8	0,49	319	365	12,5
	0,5	0,35	350	325	-7,6
6 (НН)	0,6	0,42	383	350	-9,5
6 (НН)	0,7	0,47	409	371	-10,3
	0,7	0,47	409	371	-10,3
	0,8	0,49	420	388	-8,2
	0,5	0,33	160	162	1,4
19 (НН)	0,6	0,40	167	173	3,5
19 (НН)	0,7	0,44	171	184	7,0
	0,7	0,44	171	184	7,0
	0,8	0,50	178	193	7,9
	0,5	0,33	223	223	0,1
20 (НН)	0,6	0,40	233	234	0,4
20 (НН)	0,7	0,44	239	245	2,3
	0,7	0,44	239	245	2,3
	0,8	0,50	249	254	2,0
	0,5	0,33	286	279	-2,4
21 (НН)	0,6	0,40	299	289	-3,6
21 (НН)	0,7	0,44	307	298	-3,1
	0,7	0,44	307	298	-3,1
	0,8	0,50	320	306	-4,5
	0,5	0,32	159	156	-1,8
16 (НН)	0,6	0,40	167	166	-0,6
16 (НН)	0,7	0,44	171	175	2,2
	0,7	0,44	171	175	2,2
	0,8	0,47	174	181	3,6
	0,5	0,32	221	228	2,9
17 (НН)	0,6	0,40	233	239	2,5
17 (НН)	0,7	0,44	239	250	4,3
	0,7	0,44	239	250	4,3
	0,8	0,47	244	258	5,4
	0,5	0,32	284	280	-1,4
18 (НН)	0,6	0,40	299	292	-2,5
18 (НН)	0,7	0,44	307	305	-0,8
	0,7	0,44	307	305	-0,8
	0,8	0,47	314	317	1,1
	0,5	0,40	297	315	5,9
34 (НН)	0,6	0,45	315	340	7,5
34 (НН)	0,7	0,48	326	356	8,5
	0,7	0,48	326	356	8,5
	0,8	0,50	334	367	9,1
	0,5	0,40	380	379	-0,2
35 (НН)	0,6	0,45	403	404	0,1
35 (НН)	0,7	0,48	418	430	2,7
	0,7	0,48	418	430	2,7
	0,8	0,50	428	441	2,8
	0,5	0,40	463	449	-3,2
36 (НН)	0,6	0,45	492	483	-1,9
36 (НН)	0,7	0,48	511	507	-0,7
	0,7	0,48	511	507	-0,7
	0,8	0,50	523	527	0,7

185

Окончание табл. 4.13

1	2	3	4	5	6
	0,5	0,25	179	187	4,4
25 (НН)	0,6	0,31	192	208	7,9
25 (НН)	0,7	0,37	205	230	10,8
	0,7	0,37	205	230	10,8
	0,8	0,41	215	246	12,6
	0,5	0,25	250	256	2,3
26 (НН)	0,6	0,31	269	282	4,5
26 (НН)	0,7	0,37	290	307	5,6
	0,7	0,37	290	307	5,6
	0,8	0,41	305	329	7,4
	0,5	0,25	322	286	-12,5
27 (НН)	0,6	0,31	347	306	-13,4
27 (НН)	0,7	0,37	375	326	-14,9
	0,7	0,37	375	326	-14,9
	0,8	0,41	394	347	-13,6
	0,5	0,20	325	326	0,4
31 (НН)	0,6	0,25	344	348	1,3
31 (НН)	0,7	0,30	364	369	1,4
	0,7	0,30	364	369	1,4
	0,8	0,35	385	391	1,5
	0,5	0,20	388	399	2,7
32 (НН)	0,6	0,25	411	420	2,1
32 (НН)	0,7	0,30	435	441	1,3
	0,7	0,30	435	441	1,3
	0,8	0,35	461	462	0,2
	0,5	0,20	452	442	-2,2
33 (НН)	0,6	0,25	479	461	-3,8
33 (НН)	0,7	0,30	507	481	-5,4
	0,7	0,30	507	481	-5,4
	0,8	0,35	537	500	-7,5

Приступая к статистическому анализу, отметим, что образцы № 34–36 отобраны из земляного полотна дороги Петровка – Калиновка, которая воспринимает постоянные транспортные нагрузки. Поэтому образцы, приготовленные в лаборатории, отличаются от проб, взятых из натурного участка как по способу уплотнения, так и по режиму приложения нагрузок. Грунт в образцах, отобранных из эксплуатируемого земляного полотна, претерпел изменения структуры, вследствие чего параметры d разнятся с аналогичным параметром образцов, приготовленных в лаборатории. Поэтому к статистической обработке примем данные, полученные при испытании образцов грунта, приготовленных в лаборатории.

Из этих данных сформируем 8 выборок, разделив их по относительной влажности и отношению деформаций 1/ 1с. Полученные выборки являются малыми и поэтому для их обработки применима методика ГОСТ 20512-2012 [15]. В первую очередь каждая выборка

186

проверяется на наличие грубых ошибок. Методы проверки наличия в выборке частных значений, которые можно классифицировать как грубые ошибки, приведены нами в гл. 3, а в данном случае применяется метод (табл. 1.14), регламентируемый стандартом [15, с. 5].

Таблица 4.14. Оценка выборок частных значений параметра d на наличие

грубых ошибок

№ об-					Отношение деформаций 1/ 1с
разца			0,5			0,6		0,7			0,8
		di		di-dср	di		di-dср	di	di-dср	di		di-dср
	1	2		3	4		5	2	3	4		5
		Выборки № 1–4 при относительной влажности 0,52<W/Wт 0,58
28	(НН)	0,30		0,037	0,35		0,046	0,40	0,043	0,45		0,030
29	(НН)	0,30		0,037	0,35		0,046	0,40	0,043	0,45		0,030
30	(НН)	0,30		0,037	0,35		0,046	0,40	0,043	0,45		0,030
16	(НН)	0,32		0,017	0,40		0,004	0,44	0,003	0,47		0,010
17	(НН)	0,32		0,017	0,40		0,004	0,44	0,003	0,47		0,010
18	(НН)	0,32		0,017	0,40		0,004	0,44	0,003	0,47		0,010
19	(НН)	0,33		0,007	0,40		0,004	0,44	0,003	0,50		0,020
20	(НН)	0,33		0,007	0,40		0,004	0,44	0,003	0,50		0,020
21	(НН)	0,33		0,007	0,40		0,004	0,44	0,003	0,50		0,020
14	(НН)	0,35		0,013	0,40		0,004	0,44	0,003	0,48		0,000
15	(НН)	0,35		0,013	0,40		0,004	0,44	0,003	0,48		0,000
22	(НН)	0,35		0,013	0,40		0,004	0,45	0,007	0,49		0,010
23	(НН)	0,35		0,013	0,40		0,004	0,45	0,007	0,49		0,010
24	(НН)	0,35		0,013	0,40		0,004	0,45	0,007	0,49		0,010
10	(НН)	0,35		0,013	0,40		0,004	0,45	0,007	0,49		0,010
11	(НН)	0,35		0,013	0,40		0,004	0,45	0,007	0,49		0,010
12	(НН)	0,35		0,013	0,40		0,004	0,45	0,007	0,49		0,010
7 (НН)		0,35		0,013	0,40		0,004	0,45	0,007	0,47		0,010
8 (НН)		0,35		0,013	0,40		0,004	0,45	0,007	0,47		0,010
9 (НН)		0,35		0,013	0,40		0,004	0,45	0,007	0,47		0,010
4 (НН)		0,35		0,013	0,42		0,024	0,47	0,027	0,49		0,010
5 (НН)		0,35		0,013	0,42		0,024	0,47	0,027	0,49		0,010
6 (НН)		0,35		0,013	0,42		0,024	0,47	0,027	0,49		0,010
dср1			0,337			0,396		0,443			0,48
	Sd1	0,0184			0,0195			0,0194		0,0157
	1		2,84			2,84		2,84			2,84
Sd1 1		0,0524			0,0553			0,0550		0,0445
Вывод		Вследствие того,			что условие di-dср >Sd1 1				не выполняется ни для од-
Вывод		ного частного значения di, выборки № 1–4 грубых ошибок не содержат
		[15, с. 5]
		Выборки № 5–6 при относительной влажности 0,6 W/Wт 0,68

187

Окончание табл. 4.14

	1	2		3	4		5	2	3	4		5
31	(НН)	0,20		0,025	0,25		0,30	0,30	0,35	0,35		0,30
32	(НН)	0,20		0,025	0,25		0,30	0,30	0,35	0,35		0,30
33	(НН)	0,20		0,025	0,25		0,30	0,30	0,35	0,35		0,30
25	(НН)	0,25		0,025	0,31		0,30	0,37	0,35	0,41		0,30
26	(НН)	0,25		0,025	0,31		0,30	0,37	0,35	0,41		0,30
27	(НН)	0,25		0,025	0,31		0,30	0,37	0,35	0,41		0,30
dср2			0,225			0,28		0,335			0,38
	Sd2	0,0274			0,0329			0,0383		0,0329
	2		2,07			2,07		2,07			2,07
Sd2 2			0,057			0,068		0,079			0,068
Вывод		Вследствие того,			что условие di-dср >Sd2 2				не выполняется ни для од-
Вывод		ного частного значения di, выборки № 5–8 грубых ошибок не содержат
		[15, с. 5]

Из анализа данных табл. 4.13 и 4.14 следует, что при вариации отношений деформаций 0,5 1/ 1с 0,8 частные значения параметра d и их статистики отличаются. При вариации относительной влажности также имеет место некоторое отличие параметра d, но не столь большое. Поэтому каждые из двух выборок, составленных для различных диапазонов относительных влажностей, можно проверить на принадлежность одной генеральной совокупности. Попарная оценка выборок выполняется с привлечением критериев Фишера и Стьюдента (Уильяма Госсета), которые регламентированы стандартом [15, прил.

В] (табл. 4.15).

Таблица 4.15. Оценка выборок на принадлежность одной генеральной

совокупности

Стати-		Отношение деформаций 1/ 1с
стика	0,5	0,6	0,7	0,8
Sd2/Sd1	1,489	1,687	1,974	2,096
Fa	2,64	2,64	2,64	2,64
F<Fa	Выполняется	Выполняется	Выполняется	Выполняется
t	0,758	0,751	0,680	0,696
ta	2,05	2,05	2,05	2,05
t<ta	Выполняется	Выполняется	Выполняется	Выполняется
Вывод	Вследствие выполнения условий F-критерия и t-критерия выборки по-
Вывод	парно могут быть объединены в одну генеральную совокупность

Таким образом, критерии Фишера и Стьюдента показывают, что по величине относительной влажности выборки параметров d разде-

188

лять не следует. Заметим, что с появлением экспериментальных данных о величине параметра d при более высоких влажностях грунта появятся дополнительные выборки. Оценка наших выборок и новых дополнительных может показать невозможность их объединения в одну генеральную совокупность. В этом случае величина параметра d должна будет варьироваться как в зависимости от отношений деформаций 1/ 1с, так и по величине относительной влажности. На данный момент времени таких сведений нет, вследствие чего целесообразно попарным объединением из восьми выборок сформировать четыре новые выборки. Кроме того, вариация относительной влажности учитывается при определении сцепления и угла внутреннего трения, являющихся параметрами материала в условия (4.55).

Проверка новых выборок на наличие грубых ошибок и статистическая обработка их данных приведены в табл. 4.16.

Таблица 4.16. Статистическая обработка выборок параметра d

№ об-				Отношение деформаций 1/ 1с
разца		0,5			0,6			0,7			0,8
	di		di-dср	di		di-dср	di		di-dср	di		di-dср
1	2		3	4		5	2		3	4		5
	Выборки № 1–4 при относительной влажности 0,52<W/Wт 0,68
28 (НН)	0,30		0,014	0,35		0,022	0,40		0,020	0,45		0,009
29 (НН)	0,30		0,014	0,35		0,022	0,40		0,020	0,45		0,009
30 (НН)	0,30		0,014	0,35		0,022	0,40		0,020	0,45		0,009
16 (НН)	0,32		0,006	0,40		0,028	0,44		0,020	0,47		0,011
17 (НН)	0,32		0,006	0,40		0,028	0,44		0,020	0,47		0,011
18 (НН)	0,32		0,006	0,40		0,028	0,44		0,020	0,47		0,011
19 (НН)	0,33		0,016	0,40		0,028	0,44		0,020	0,50		0,041
20 (НН)	0,33		0,016	0,40		0,028	0,44		0,020	0,50		0,041
21 (НН)	0,33		0,016	0,40		0,028	0,44		0,020	0,50		0,041
14 (НН)	0,35		0,036	0,40		0,028	0,44		0,020	0,48		0,021
15 (НН)	0,35		0,036	0,40		0,028	0,44		0,020	0,48		0,021
22 (НН)	0,35		0,036	0,40		0,028	0,45		0,030	0,49		0,031
23 (НН)	0,35		0,036	0,40		0,028	0,45		0,030	0,49		0,031
24 (НН)	0,35		0,036	0,40		0,028	0,45		0,030	0,49		0,031
10 (НН)	0,35		0,036	0,40		0,028	0,45		0,030	0,49		0,031
11 (НН)	0,35		0,036	0,40		0,028	0,45		0,030	0,49		0,031
12 (НН)	0,35		0,036	0,40		0,028	0,45		0,030	0,49		0,031
7 (НН)	0,35		0,036	0,40		0,028	0,45		0,030	0,47		0,011
8 (НН)	0,35		0,036	0,40		0,028	0,45		0,030	0,47		0,011
9 (НН)	0,35		0,036	0,40		0,028	0,45		0,030	0,47		0,011
4 (НН)	0,35		0,036	0,42		0,048	0,47		0,050	0,49		0,031

189

Окончание табл. 4.16

	1	2		3	4		5	2		3	4		5
5 (НН)		0,35		0,036	0,42		0,048	0,47		0,050	0,49		0,031
6 (НН)		0,35		0,036	0,42		0,048	0,47		0,050	0,49		0,031
31	(НН)	0,20		0,114	0,25		0,122	0,30		0,120	0,35		0,109
32	(НН)	0,20		0,114	0,25		0,122	0,30		0,120	0,35		0,109
33	(НН)	0,20		0,114	0,25		0,122	0,30		0,120	0,35		0,109
25	(НН)	0,25		0,064	0,31		0,062	0,37		0,050	0,41		0,049
26	(НН)	0,25		0,064	0,31		0,062	0,37		0,050	0,41		0,049
27	(НН)	0,25		0,064	0,31		0,062	0,37		0,050	0,41		0,049
	dср		0,314			0,372			0,420			0,459
	Sd		0,050			0,053			0,050			0,046
			2,94			2,94			2,94			2,94
Sd			0,148			0,155			0,148			0,134
Вывод		Вследствие того, что условие di-dср >Sd не выполняется ни для од-
Вывод		ного частного значения di, выборки № 1–4 грубых ошибок не содержат
		[15, с. 5]
V, %			16,03			14,17			11,95			9,94
dmin			0,295			0,352			0,401			0,442
dmax			0,333			0,392			0,439			0,477

Максимальные значения параметра d, дополненные точкой dmax=0,5 при 1/ 1с=1, могут быть вычислены по эмпирической формуле

					2
dmax	1,3689	1	0,6882	1		0,1807.	(4.64)

		1с
		1с		1с

Используя данные статистической обработки, средние и минимальные значения параметра d определяются по формулам

		1						2
dср 1,2988				0,6486			1			0,1728.	(4.65)

	1с
						1с
									2
dmax 1,2287				1			1			0,165.	(4.66)

			1с		0,609
							1с

Из анализа зависимостей (1.64) – (1.66) следует, что параметр d связан с отношением деформации 1, которая может быть принята в качестве условной меры начала пластичности, к предельной деформации 1с, при которой определяются параметры Кулона – Мора.

190

4.4. Применение теории усталости для расчета параметров предельной прямой Кулона – Мора при воздействии повторных нагрузок

Под воздействием нагрузки в структуре материалов накапливаются повреждения, а также протекают процессы пластического роста трещин. Это характерно как для монолитных материалов, так и для дискретных сред. В дискретном материале рост поврежденности и уменьшение сплошности можно подтвердить увеличением пористости и уменьшением плотности сухого грунта (материала). Развитие дефектов приводит к структурным изменениям, в результате которых уменьшается степень насыщенности объема грунта жесткими структурными связями. Вследствие этого по мере роста поврежденности происходит снижение параметров прочности и деформируемости. Процесс постепенного увеличения повреждений и уменьшения сплошности материала, приводящий к изменению его прочности и деформируемости, называют усталостью.

Величина снижения прочности зависит от ряда факторов, к которым можно отнести:

–вид материала (разновидность грунта);

–показатели физических свойств материала, при которых прикладываются повторные нагрузки;

–значения компонент тензора напряжений, обусловленные величиной многократно прикладываемой нагрузки:

–количество циклов «нагрузка – разгрузка», приложенных к материалу в процессе испытаний.

Последние два фактора позволяют сделать вывод, что величина снижения параметров прочности зависит от истории приложения к материалу повторных нагрузок. Вследствие того, что параметры прочности материала зависят от истории приложения нагрузки, то усталость является наследственным процессом. Значит, при построении усталостной модели снижения прочности или роста поврежденности можно применить правила интегрального исчисления.

При сдвиге к параметрам прочности дискретных материалов и грунтов относят параметры предельной прямой Кулона – Мора, сцепление и угол внутреннего трения. В настоящее время установлено, что в процессе приложения повторных нагрузок эти параметры уменьшаются. Нормативные документы по проектированию дорожных одежд [46, 47] содержат функции, заданные таблично и позво-

191

ляющие определять значения сцепления и угла внутреннего трения от суммарного числа приложения расчетной нагрузки, разновидности грунта и относительной влажности связных грунтов. Эти табличные функции можно использовать для определения параметров модели.

Для применения аппарата теории наследственности необходимым условием является существование функций.

N;n;k

у0

;

N;n;k

у0

;W , (4.67)

отн

где сN и cn – сцепление грунта после приложения повторных нагрузок числом N и n, причем N>>n, Па; N и n – углы внутреннего трения грунта после приложения повторных нагрузок числом N и n, о; ij – компоненты тензора напряжений, которые при испытаниях в динамическом стабилометре являются главными напряжениями, Па; kу0 – коэффициент уплотнения грунта или дискретного материала в образце в начале испытания; Wотн – относительная влажность связного грунта в процессе испытаний, определяемая отношением влажности грунта к влажности на границе текучести.

Функциональные зависимости (4.67) постулируют влияние на параметры сопротивления сдвигу характеристик напряженного состояния величины компонент тензора напряжений и числа нагрузок, обуславливающих возникновение такого тензора, а также физического состояния материала в образце. При этом начальная структура материала оценивается величиной коэффициента уплотнения до приложения нагрузки.

Отметим, что сцепление и угол внутреннего трения грунта коррелируют с коэффициентом уплотнения [52, с. 52]. Учитывая такую зависимость, можно предположить существование функций, альтернативных зависимостям (4.67), которые имеют вид

уN

;

, (4.68)

отн

kуn

где kуN и kуn – коэффициенты уплотнения грунта или дискретного материала в образце после приложения повторных нагрузок в количествах N и n соответственно.

Величину коэффициента уплотнения после приложения повторных нагрузок в количестве N можно определить по формулам


kуN	dN		,	(4.69)

		dmax

192

где dN – плотность сухого грунта после приложения N-го количества нагрузок, т/м3; dmax – максимальная стандартная плотность сухого грунта, определяемая в приборах стандартного уплотнения, т/м3.

s 1 nN

1 nN

(4.70)

уN

1 n

min

1 n

min

где s – плотность частиц грунта, т/м3; nN – пористость после приложения N-го количества нагрузок; nmin – минимальное значение пористости, соответствующее максимальной стандартной плотности сухого грунта.

kуN	s	1 emin	1 emin	,	(4.71)
	1 eN	s
			1 eN

где eN – коэффициент пористости после приложения N-го количества нагрузок; emin – минимальное значение коэффициента пористости, соответствующее максимальной стандартной плотности сухого грунта.

Из анализа зависимостей (4.69) – (4.71) следует, что для уменьшения коэффициента уплотнения в процессе приложения повторных нагрузок необходимо либо увеличение пористости и коэффициента пористости, либо уменьшение плотности сухого грунта. Так как пористость, коэффициент пористости и плотность сухого грунта характеризуют его структуру, то процесс уменьшения коэффициента уплотнения при реализации повторных нагрузок является следствием структурных изменений. В этом случае должна иметь место функция

kуN	f ij N;n;kу0 .	(4.72)

kуn

Следует заметить, что зависимость (4.72) в некотором смысле подобна функциям наследственных теорий, связывающих деформации материала с напряженным состоянием, временем воздействия нагрузки, показателями физических и механических свойств материала. В отличие от функций наследственных теорий выражение (4.72) постулирует зависимость коэффициента уплотнения, описывающего структуру среды, от суммарного числа нагрузок, а не от функции времени. Формулы (4.67) предполагают зависимость параметров сопротивления сдвигу от числа нагрузок, а одна из наследственных теорий – теория старения – предполагает зависимость механических характеристик от возраста материала. Поэтому усталость материала носит наследственный характер, но при воздействии повторных нагрузок для расчета параметров прочности необходимо применять функ-

193

ции числа нагрузок, а не времени, как это принято при статическом длительном воздействии.

Учитывая выполненные рассуждения, предпримем попытку вывода функций (4.67), применяя принципы наследственных теорий. В качестве математического аппарата этих теорий применяется интегральное исчисление, а подынтегральное выражение называется ядром ползучести, релаксации и т.п. В нашем случае интегральное исчисление применяется для расчета изменения параметров сопротивления сдвигу при воздействии повторной нагрузки. В связи с чем подынтегральное выражение назовем ядром усталости.

В качестве ядра усталости примем простые степенные функции, в соответствии с которыми приращение сцепления и угла внутреннего трения от n-го воздействия (от нагрузки с порядковым номером n) определяется по формуле

п 1

;

п 1

(4.73)

где сn и n – соответственно приращения сцепления и угла внутреннего трения от п-го воздействия нагрузки; ас и а – коэффициенты, учитывающие уровень напряженного состояния, вид материала, его физическое состояние по плотности влажности и т.п.

с	n	b	пdc ;		n	b	пd ,	(4.74)
	n	c			n

где bc, dc и b , d – соответственно коэффициенты, учитывающие уровень напряженного состояния, вид материала, его физическое состояние по плотности влажности и т.п.

В процессе усталости параметры сопротивления сдвигу уменьшаются, вследствие чего интегральные выражения примут вид

сN

сn

;

, (4.75)

1 ас

n 1dn

1 а

n 1dn

где сn и n – величина сцепления и угла внутреннего трения после приложения n-го числа нагрузок (n<<N).

1 b

пd dn

ndc dn

;

. (4.76)

Выполнив интегрирование подынтегральных выражений в зависимостях (4.75) и (4.76), получим

				N
сN	сn	1 ас	ln		;

				n

Ndс 1 ndс 1

сN сn 1 bc		;
	dс 1

				N
N	n	1 а	ln		.	(4.77)

				n

Nd 1 nd 1

N	n 1 b		. (4.78)
N	n 1 b	d 1	. (4.78)
		d 1

194

В том случае если параметры сN и N можно связать с величиной сцепления и угла внутреннего трения от первого по счету приложения нагрузки, то есть с с1 и 1, то формулы (4.77) и (4.78) примут вид

сN с1 1 ас ln N ;

N 1 1 a ln N ,

(4.79)

где N – суммарное число приложенных расчетных нагрузок, вызывающих возникновение в наиболее опасной точке рассчитываемого элемента дорожной конструкции наибольших по условию Кулона – Мора касательных напряжений, расчетные единицы.

		dс	1				d 1
	N				N	n 1 b N		1 . (4.80)
сN с1 1 bc	N	dс		1 ;	N	n 1 b N		1 . (4.80)
		dс	1				d 1

Таким образом, согласно зависимостям (4.79) снижение параметров предельной прямой Кулона – Мора описывается логарифмической функцией, а в соответствии с формулами (4.80) – степенным выражением.

В тех случаях, когда сN и N нельзя связать с с1 и 1, то их значения следует вычислять в два этапа. Первый этап состоит в том, что значения сn и n связываются с параметрами с1 и 1 логарифмической. В этом случае если число нагрузок n сравнительно мало и на участке 1<N≤n нет особой надобности в точном прогнозе пластических деформаций (в случае, когда n 1000), то связь сn и n с с1 и 1 целесообразно искать в виде

сn	с1		n	с1 1 ac1 lnn ,	(4.81)
		1 ac1	n 1dn
			1

где ac1 – параметр логарифмической модели, характеризующий снижение сцепления в интервале 1≤N≤n и учитывающий уровень напряженного состояния и вид материала.

		1 a		n		1 a		lnn ,	(4.82)
n			1	n 1dn			1
	1			1	1

где a 1 – параметр логарифмической модели, характеризующий снижение угла внутреннего трения в интервале 1≤N≤n и учитывающий уровень напряженного состояния и вид материала.

На втором этапе вычисляются параметры сN и N, которые связаны с величинами сn и n. Этот расчет выполняется по формулам (4.77) или (4.78), а общая формула представляется произведением функций (4.81) или (4.82) с соответствующей формулой (4.77) или (4.78).

195

Так произведения (4.81) и (4.82) с соответствующей зависимостью (4.77) приводят к выражениям

						N
сN	с1	1 ac1	lnn 1 ас2	ln			.	(4.83)
сN	с1	1 ac1	lnn 1 ас2	ln		n	.	(4.83)
						n
					N
N 1 1 a 1 lnn 1 а 2				ln			.	(4.84)
N 1 1 a 1 lnn 1 а 2				ln			.	(4.84)
					n

Формулы (4.83) и (4.84) связывают сN и N с с1 и 1, но в отличие от зависимостей (4.79) содержат два параметра материала.

Произведения (4.81) и (4.82) с соответствующей зависимостью (4.78) приводят к сложным функциям, которые имеют вид

1 a

lnn

dс 1

1 b

(4.85)

dс 1

d 1

1 a

lnn 1 b

(4.86)

d 1

Формулы (4.85) и (4.86) так же, как и зависимости (4.78), связывают параметры сN и N с с1 и 1, но включают в себя три параметра, а не два. Для определения вида функций усталости и их коэффициентов необходимо выполнить анализ экспериментальных данных, полученных при испытаниях материалов и грунтов в условиях приложения повторных нагрузок. При этом необходимо отметить, что величина параметров сопротивления сдвигу зависит:

–от вида материала и показателей его физических свойств (гранулометрический состав, плотность, влажность);

–параметров испытания, к которым относят условия осушения тестируемого образца (схема испытания – дренированная или недренированная), времени воздействия каждой нагрузки и продолжительности отдыха между силовыми воздействиями, характера приложения

иснятия каждой нагрузки во времени (форма эпюр бывает прямоугольная, треугольная или по синусоиде);

–уровня напряженного состояния, который при трехосном сжатии характеризуется величиной девиатора напряжений и значением удерживающего напряжения;

–количества приложенных нагрузок.

Экспериментальные исследования по определению влияния усталостных процессов, развивающихся в грунтах в условиях приложения повторных нагрузок, на параметры сопротивления сдвигу выполнены в работах В.Д. Казарновского, В.М. Смирнова, Ю.И. Косарева [23,

196

с. 89-90], Е.А. Петрушина [42, с. 94], В.М. Смирнова, С.Н. Дорогутиной 53, с. 124]. Благодаря этим исследованиям специалистами дорожной отрасли сформировано общепринятое мнение о количественном изменении сцепления и угла внутреннего трения при воздействии повторной нагрузки с числом приложений, варьирующемся в диапазоне 1 N 106 и при N>106, которое приведено в нормативах [46, 47] в виде табличных функций. В нормативных документах значения сцепления округлены до 1 кПА, а в работах Е.А. Петрушина [42, с. 94] и В.М. Смирнова и С.Н. Дорогутиной [53, с. 124] функция падения сцепления при росте числа приложенных нагрузок задана графически. В статье В.Д. Казарновского, В.М. Смирнова, Ю.И. Косарева [23, с. 8990] величина сцепления принята с точностью 0,1 кПа. Поэтому анализ данных, представленных в работах [23, 42, 53], позволит более точно определить параметры материала в зависимостях (4.83) – (4.86) для песчаных и глинистых грунтов, чем анализ функций, заданных таблично в нормативных документах [46, 47].

Анализ данных работы [23, с. 89-90] показывает, что расчет параметров песков можно выполнить по формулам (4.81) и (4.82).

Таблица 4.17. Функциональная зависимость параметров предельной

прямой Кулона – Мора от числа приложенных нагрузок и параметры песка

	Содержание	Степень
Вид	пылеватых и	Степень												R2
Вид	пылеватых и	влаж-				Формула					Параметры			R2
песка	глинистых	ности Sr
	частиц, %	ности Sr
	частиц, %
1	2	3						4				5		6
		0									1, о		34,4	0,997
		0						1 a		lnN	a		0,0043	0,997
		0,3			N			1 a		lnN	1, о		35,7	0,999
		0,3			N	1					a		0,0082	0,999
											a		0,0082
Круп-		1,0									1, о		35,1	0,998
Круп-	0	1,0									a		0,0137	0,998
ный
		0									с1, кПа		4,2	0,994
											с1, кПа		4,2
							1 а			ln N	aс		0,0167
											aс		0,0167
		0,3	с	N		с			с		с1, кПа		4,6	0,997
		0,3	с			с					aс		0,0113	0,997
						1					aс		0,0113
		1,0									с1, кПа		2,9	0,998
		1,0									aс		0,0132	0,998
											aс		0,0132

197

Продолжение табл. 4.17

1	2	3						4					5		6
		0,3						1 a		lnN	1, о			36,3	0,998
		0,3			N			1 a		lnN	a			0,0078	0,998
		1,0			N	1					1, о			37,4	0,997
Круп-											1, о			37,4
Круп-	5										a			0,0132
ный	5	0,3									с1, кПа			4,3	0,984
ный											с1, кПа			4,3
			с	N		с	1 а		с	ln N	aс			0,0143
											aс			0,0143

		1,0				1					с1, кПа			3,0	0,989
		1,0									aс			0,0321	0,989
											aс			0,0321
		0									1, о			31,6	1
		0						1 a		lnN	a			0,0055	1
		0,3			N			1 a		lnN	1, о			33,1	1
		0,3			N	1					a			0,0076	1
											a			0,0076
		1,0									1, о			32,3	0,998
	0	1,0									a			0,014	0,998
											a			0,014
		0									с1, кПа			4,3	0,964
											с1, кПа			4,3
							1 а			ln N	aс			0,0126
											aс			0,0126
		0,3	с	N		с			с		с1, кПа			4,1	0,994
		0,3	с			с									0,994
Сред-						1					aс			0,0256
ний		1,0									с1, кПа			2,8	0,999
		1,0									aс			0,028	0,999
											aс			0,028
		0,3						1 a		lnN	1, о			35,1	0,999
		0,3			N			1 a		lnN	a			0,0064	0,999
		1,0			N	1					1, о			33,1	0,998
											1, о			33,1
	5										a			0,0133
	5	0,3					1 а			ln N	с1, кПа			4,7	1
											с1, кПа			4,7
			с	N		с			с		aс			0,0277
			с			с
		1,0				1					с1, кПа			4,6	0,999
		1,0									aс			0,0327	0,999
											aс			0,0327
		0									1, о			31,6	1
		0						1 a lnN			a			0,0055	1
					N			1 a lnN				о		31,6
		0,3			N	1						1,			0,999
		0,3									a			0,0117	0,999
Мел-		1,0									1, о			31,6	0,999
Мел-	0	1,0									a			0,0152	0,999
кий
		0									с1, кПа			5,6	1
											с1, кПа			5,6
							1 а			ln N	aс			0,0078
		0,3	с	N		с			с		с1, кПа			5,9	1
		0,3	с			с					aс			0,0147	1
						1					aс			0,0147
		1,0									с1, кПа			3,1	0,999
		1,0									aс			0,0253	0,999
											aс			0,0253

198

Окончание табл. 4.17

1	2	3						4				5		6
		0,3						1 a		lnN	1, о		34,4	0,999
		0,3			N			1 a		lnN	a		0,0091	0,999
		1,0			N	1					1, о		33,1	0,996
											1, о		33,1
	5										a		0,0198
											a		0,0198
		0,3									с1, кПа		5,3	0,994
											с1, кПа		5,3
			с	N		с	1 а		с	ln N	aс		0,017
											aс		0,017

		1,0				1					с1, кПа		4,3	0,949
Мел-		1,0									aс		0,0227	0,949
Мел-											aс		0,0227
кий		0,3						1 a		lnN	1, о		32,3	0,999
		0,3			N			1 a		lnN	a		0,0079	0,999
		1,0			N	1					1, о		32,3	0,996
											1, о		32,3
	8										a		0,0174
											a		0,0174
		0,3									с1, кПа		7,4	0,984
											с1, кПа		7,4
			с	N		с	1 а		с	ln N	aс		0,0166
											aс		0,0166

		1,0				1					с1, кПа		4,1	0,998
		1,0									aс		0,0468	0,998
											aс		0,0468

Аналогично подбираются зависимости сцепления и угла внутреннего трения от числа повторных нагрузок для супесей, суглинков

иглин. Отметим, что для этих видов грунтов наиболее приемлемыми являются двухпараметрические логарифмические зависимости (4.83)

и(4.84) или трехпараметрические функции (4.85) и (4.86) (табл. 4.18 и 4.19). Кроме того, для этих целей можно применять табличные функции нормативных документов [46, 47].

Таблица 4.18. Параметры функциональных зависимостей параметров

предельной прямой Кулона – Мора от числа приложенных нагрузок для суглинков и глин

Влаж-

ность

Формула

Параметры

W/Wт

d 1

1, о

1 a

lnn 1 b

;

a 1

-0,0241

0,6

d 1

0,2512

n 1000

-1,116

d 1

1, о

1 a

lnn 1 b

;

a 1

-0,414

0,65

d 1

0,2385

n 1000

-1,113

199

Продолжение табл. 4.18

d 1

1, о

1 a

lnn 1 b

;

a 1

-0,414

0,65

d 1

0,2385

n 1000

-1,113

d 1

1, о

1 a

lnn 1 b

;

a 1

-0,0523

0,7

d 1

0,2205

n 1000

-1,108

d 1

1, о

1 a

lnn 1 b

;

a 1

-0,0483

0,75

d 1

0,3525

n 1000

-1,137

d 1

1, о

1 a

lnn 1 b

;

a 1

-0,0557

0,8

d 1

0,5477

n 1000

-1,174

d 1

1, о

11,5

1 a

lnn 1 b

;

a 1

-0,0649

0,9

d 1

0,5123

n 1000

-1,154

dс 1

с1, МПа

0,030

1 a

lnn 1 b

;

с1

-0,0241

0,6

dс 1

bс

0,186

n 1000

dс

-1,101

dс 1

с1, МПа

0,024

1 a

lnn 1 b

;

с1

-0,0302

0,65

dс 1

bс

0,204

n 1000

dс

-1,105

dс 1

с1, МПа

0,019

1 a

lnn 1 b

;

с1

-0,0457

0,7

dс 1

bс

0,229

n 1000

dс

-1,112

dс 1

с1, МПа

0,015

1 a

lnn 1 b

;

с1

-0,0579

0,75

dс 1

bс

0,236

n 1000

dс

-1,114

dс 1

с1, МПа

0,011

1 a

lnn 1 b

;

с1

-0,0526

0,8

dс 1

bс

0,687

n 1000

dс

-1,185

200

Окончание табл. 4.18

dс 1

с1, МПа

0,008

с 1 a

lnn 1 b

;

с1

-0,0724

0,9

dс 1

bс

0,985

n 1000.

dс

-1,205

Таблица 4.19.

Параметры

функциональных

зависимостей сцепления

и угла внутреннего трения супесей от числа приложенных нагрузок

Относитель-

ная влаж-

Формула

Параметры

ность W/Wт

d 1

1, о

1 a

lnn 1 b

;

a 1

-0,0483

0,6

-0,1972

n 1000

-1,101

d 1

1, о

1 a

lnn 1 b

;

a 1

-0,0503

0,65

-0,1778

n 1000

-1,096

d 1

1, о

1 a

lnn 1 b

;

a 1

-0,0476

0,7

-0,1778

n 1000

-1,096

d 1

1, о

1 a

lnn 1 b

;

a 1

-0,0496

0,75

-0,17

n 1000

-1,093

d 1

1, о

1 a

lnn 1 b

;

a 1

-0,0468

0,8

-0,17

n 1000

-1,093

d 1

1, о

1 a

lnn 1 b

;

a 1

-0,0511

0,85

-0,2302

n 1000

-1,112

d 1

1, о

1 a

lnn 1 b

;

a 1

-0,0526

0,9

-0,3149

n 1000

-1,135

201

Окончание табл. 4.19

dс 1

с1, кПа

1 a

lnn 1 b

;

с1

-0,0207

0,6

dс 1

bс

0,29505

n 1000

dс

-1,128

dс 1

с1, кПа

1 a

lnn 1 b

;

с1

-0,0334

0,65

dс 1

bс

0,33408

n 1000

dс

-1,131

dс 1

с1, кПа

1 a

lnn 1 b

;

с1

-0,0362

0,7

dс 1

bс

0,23556

n 1000

dс

-1,114

dс 1

с1, кПа

1 a

lnn 1 b

;

с1

-0,0395

0,75

dс 1

bс

0,33313

n 1000

dс

-1,137

dс 1

с1, кПа

1 a

lnn 1 b

;

с1

-0,0434

0,8

dс 1

bс

0,26933

n 1000

dс

-1,12

dс 1

с1, кПа

1 a

lnn 1 b

;

с1

-0,0483

0,85

dс 1

bс

0,17538

n 1000

dс

-1,097

dс 1

с1, кПа

1 a

lnn 1 b

;

с1

-0,0724

0,9

dс 1

bс

0,09414

n 1000

dс

-1,062

Вмоделях наследственной усталости, представленных в табл.

4.17– табл. 4.19, коэффициент уплотнения грунтов в начале испытания составляет 0,98 – 1. При более низких коэффициентах уплотнения параметры сопротивления сдвигу должны быть меньше. Учесть влияние коэффициента уплотнения на величину сцепления и угла внутреннего трения, можно применяя результаты исследований работы [52, с. 52]. В соответствии с формулами Ю.А. Покутнева угол внутреннего трения прямо пропорционален коэффициенту уплотнения, а сцепление – корню квадратному из коэффициента уплотнения, возведенного в третью степень (куб) [52, с. 52]. Следовательно, влияние степени уплотнения грунтов на параметры предельной прямой Куло-

202

на – Мора можно учесть вводом в зависимости (4.79) и (4.85), (4.86) функций коэффициента уплотнения. Тогда для песчаных грунтов сцепление и угол внутреннего трения можно определить по формулам

1,5

1 а

lnN ;

у0

1 a

lnN .

(4.87)

у0

Для супесей суглинков и глин параметры предельной прямой Кулона – Мора определяются по формулам

dс 1

1,5

1 a

lnn 1 b

(4.88)

у0

dс 1

d 1

у0

1 a

lnn 1 b

(4.89)

d 1

При проектировании дорожных конструкций в соответствии с нормами [46, 47] расчет покрытий и оснований по критерию сопротивления сдвигу не выполняется. Видимо считается, что щебеночные и гравийные материалы, а также их смеси с песком обладают достаточным сопротивлением сдвигу. Экспериментальные данные, полученные зарубежными коллегами, показывают, что параметры предельной прямой Кулона – Мора имеют достаточно высокие значения. Однако такие материалы применяют в основаниях, а для дорог низких категорий – в покрытиях. Поэтому по сравнению с земляным полотном и песчаными дополнительными слоями оснований такие слои воспринимают более высокие давления. Значит, касательные напряжения, возникающие в этих слоях, имеют более высокие значения, чем в грунтах земляного полотна и песчаных дополнительных слоях оснований. Стендовые испытания дорожных конструкций со сравнительно тонким покрытием показывают, что слои из дискретных материалов накапливают наибольшую отметочную деформацию [68]. Поэтому конструктивные слои из дискретных материалов необходимо рассчитывать на сопротивление сдвигу. Для расчета главных напряжений можно использовать модифицированные нами модели И.И. Кандаурова (2.45) и (2.46) или М. Хара (2.47) и (2.48). Параметры сопротивления дискретных материалов сдвигу можно определить на основе анализа экспериментальных работ.

Большой объем экспериментальных исследований по определению показателей механических свойств щебня из гравия опубликован в отчете [120, с. 42–52]. Необходимо отметить, что на параметры сопротивления дискретных материалов сдвигу оказывают количественное влияние различные факторы (табл. 4.20) [120, с. 42].

203

Таблица 4.20. Факторы, влияющие на сопротивление сдвигу и параметры

предельной прямой Кулона – Мора для дискретных материалов

Фактор	Варьирование	Характер влияния на:
	Варьирование	сопротивле-		угол внутрен-
	фактора	сопротивле-	сцепление	угол внутрен-
	фактора	ние сдвигу	сцепление	него трения
Плотность	Увеличение	Существенно возрастает
Степень водона-	Уменьшение	Существенно возрастает		Не влияет
сыщения
Максимальный	Увеличение от		Возрастает
размер частиц	9,5 до 37,5 мм		Возрастает
размер частиц	9,5 до 37,5 мм
Содержание	Увеличение от	Возрастает	Сильно	Возрастает
пылеватых и	1 до 9 %	Возрастает	возрастает	Возрастает
глинистых час-	Увеличение от		Уменьшается
тиц	9 до 15 %		Уменьшается
тиц	9 до 15 %
Пластичность	Изменение от
пылеватых и	непластичной		Уменьшается
глинистых час-	до пластичной		Уменьшается
глинистых час-	до пластичной
тиц	консистенции
Текстура по-	Изменение от	Увеличивает-	Не уста-
верхности час-	гладкой к ше-	Увеличивает-	Не уста-	Увеличивается
верхности час-	гладкой к ше-	ся	новлено	Увеличивается
тиц	роховатой
Прочность час-	Уменьшение		Уменьшается
тиц
	Изменение от
Форма частиц	округлой до	Увеличение	Не влияет	Увеличение
	угловатой

В работе [120] сообщается, что наиболее значимыми факторами являются относительная плотность и степень насыщения водой (табл. 4.21) и приводятся эмпирические формулы для расчета сцепления и угла внутреннего трения [120, с. 45].

Таблица4.21. Сцеплениеиугол внутреннеготрениядискретныхматериалов

Классификация	Относительная	Степень водона-	Параметры сопротивле-
гранулирован-	плотность (сте-	сыщения (коэф-	ния сдвигу
гранулирован-	плотность (сте-	сыщения (коэф-
ного материала	пень плотности),	фициент водона-	с, кПа	, о
ного материала	%	сыщения), %	с, кПа	, о
	%	сыщения), %
1	2	3	4	5
G1	82,6	92,0	10,0	50,5
G1	84,0	30,0	30,5	54,2
G1	84,0	90,0	16,0	53,2
G1	84,7	47,0	58,0	56,7
G1	85,3	41,0	44,0	56,1
G1	87,0	31,0	96,0	56,0

204

Окончание табл. 4.21

1	2	3	4	5
G1	87,0	38,0	76,0	55,2
G1	87,0	40,0	63,0	55,8
G1	86,9	55	53,0	55,1
G1	87,0	90,0	16	53,0
G2	80,7	55,7	68,1	48,6
G2	80,7	78,0	28,1	49,4
G2	82,6	37,9	120,5	51,4
G2	82,5	63,2	35,6	50,7
G2	82,6	72,6	25,7	50,1
G2	84,5	72,6	51,1	51,4
G2	84,5	43,5	102,8	54,6
G2	80,7	33,4	94,9	53,1
G2	84,5	100,0	43,0	47,7
G2	85,3	41,0	44,0	56,1
G2	86,2	37,0	70,0	52,7
G2	86,1	42,0	48,0	53,1
G2	85,1	82,0	21,0	49,8
G2	85,6	36,0	45,0	52,1
G4	73,8	24,6	74,2	51,0
G4	73,8	41,0	51,2	48,2
G4	74,7	47,0	35,0	52,3
G4	73,5	70,0	18,0	49,8
G5	73,5	70,0	18,0	49,8
G5	74,5	73,0	4,0	41,0
G5	72,7	46,0	18,0	43,6
G5	73,1	51,0	36,0	38,0
G5	73,5	77,0	43,0	43,0
G10	73,5	26,2	72,4	45,6
G10	73,5	41,2	28,6	38,4

Примечание. В скобках приведено наименование показателя в терминологии ГОСТ 25100.

Классификация гранулированных материалов, применяемая в зарубежных стандартах, приведена в работе [120, c. 7–9]. В зарубежной практике сцепление и угол внутреннего трения определяют монотонными трехосными испытаниями. Поэтому данные табл. 4.20 позволяют определить значения сцепления и угла внутреннего трения, соответствующие однократному приложению нагрузки, то есть с1 и 1. Анализ данных табл. 4.19 позволяет сделать вывод, что к уменьшению параметров предельной прямой Кулона – Мора приводит:

– изменение формы зерен каменного материала от угловатой к более округлой;

205

–уменьшение их шероховатости;

–увеличение содержания пылеватых и глинистых частиц.

Впроцессе эксплуатации дорожных одежд со слоями из щебеночных

игравийных материалов происходит износ каменного материала (рис. 4.21). Вследствие этого в щебне и гравии протекают все перечисленные нами процессы. Поэтому

проверку сопротивления

	Рис. 4.21. Износ щебня в основании дорожной	сдвигу слоев из дискрет-
	одежды
		ных материалов необхо-

димо выполнять с учетом принципов теории наследственной усталости. Надежные экспериментальные данные можно получить при помощи динамических трехосных испытаний, позволяющих реализовывать многократное приложение нагрузки. В настоящее время такого оборудования в РФ мало, вследствие чего необходимо искать приближение. Ориентировочное значение минимальной величины сцепления сmin можно определить, используя данные ранее действовавшего нормативного документа ВСН 46-83 [22, рис. 3.8], которое составляет 0,55 от с1. Принимая, что в процессе реализации повторных нагрузок сцепление изменяется по логарифмическому закону и достигает минимальной величины при приложении 106 нагрузок, эмпирические формулы можно получить подбором прямой в полулогарифмических координатах. Такая эмпирическая формула имеет вид

сN с1	1 0,0326 lnN .	(4.90)
Величина сцепления с1	принимается по табл. 4.21 для соответст-

вующего типа материала и параметров его физического состояния. Выполняя определение с1, данные табл. 4.21 можно интерполировать.

Функцию изменения угла внутреннего трения от числа повторных нагрузок для зернистых материалов можно установить только экспериментально. Поэтому расчет по сопротивлению сдвигу щебеночных оснований можно выполнять только при допущении N= 1.

206

4.5. Расчет безопасных давлений на грунты земляного полотна и слои дорожной одежды из дискретных материалов

При расчете безопасных и предельных давлений на грунтовые основания и слои дорожных конструкций из дискретных материалов применяют различные аналитические и феноменологические методы. К аналитическим методам механики грунтов, следуя классификации В.Г. Березанцева [2, 3], относим:

1. Метод линейно деформируемой среды, классическими решениями которого являются формулы Н.П. Пузыревского [48], Н.Н. Маслова [34], И.В. Яропольского [61], предназначенные для расчета безопасных и предельных давлений от нагрузок, распределенных по полосе. Суть метода состоит в том, что из принятого условия пластичности, как правило, критерия Кулона – Мора в форме уравнения (4.30) и подстановки в него выражений для вычисления главных напряжений, выводится зависимость для расчета безопасного или предельного давления. Безопасным считается величина давления, при котором в наиболее опасной точке основания возникает предельное состояние по условию пластичности, положенному в основу расчета. Предельными считаются давления, при передаче которых в основании возникает некоторая пластическая область. По контуру этой области возникает предельное состояние, а внутри контура имеет место запредельное состояние по критерию пластичности, положенному в основу расчета. Численное значение предельного давления зависит от принятой глубины распространения неустойчивой (пластической) области грунта в основании. Чем больше эта область пластических сдвигов, тем выше величина предельного давления.

2.Метод поверхностей скольжения, в котором предполагается, что сдвиг грунта происходит по некоторой траектории, называемой поверхностью или линией скольжения. Целью решения является определение коэффициента устойчивости и нахождения его минимального значения. Коэффициент устойчивости определяется отношением моментов удерживающих и сдвигающих сил [2, 3].

3.Метод предельного равновесия грунтов, представляющий собой решения, развивающие теорию поверхностей скольжения. Начало этого метода заложено в работах Прандтля – Рейснера, получивших так называемую двухчленную зависимость для расчета предельных давлений [112, 114]. Развитие метода предельного равновесия выполнил К. Терцаги, введя в двучленную зависимость Прандтля – Рейсне-

207

ра третье слагаемое, учитывающее влияние на величину предельного давления боковой пригрузки [118]. Метод предельного равновесия грунтов нашел широкое применение при проектировании фундаментов и насыпей земляных сооружений. Решение различных задач методами предельного равновесия грунтов является целью современных кандидатских [7, 40] и докторских [29] исследований. Решения метода предельного равновесия грунтов, полученные разными авторами, дают различные результаты даже для одинаковых нагрузок. Причины такого отличия разные и могут обуславливаться, например, постулированием значительного или наоборот незначительного влияния боковой пригрузки на величину предельного давления.

Феноменологические методы мы разделяем на две группы:

1.Методы, основанные на применении калифорнийского числа несущей способности грунта.

2.Методы, основанные на применении теории приспособляемости, в которой пределы приспособляемости гранулированных материалов связаны с числом приложения нагрузок эмпирическими формулами, полученными линеаризацией или аппроксимацией данных трехосных динамических испытаний повторной нагрузкой.

Безопасные и предельные давления, вычисляемые одним из представленных методов, могут быть близки к так называемым критическим нагрузкам. Критические нагрузки Н.М. Герсеванова можно рассматривать в качестве предельных давлений, которые разделяют зависимость осадки от давления на три стадии: уплотнения, сдвигов и потери несущей способности. Поэтому критические нагрузки Н.М. Герсеванова можно считать некоторым аналогом абсолютных пределов, констатирующих факт коренного изменения характера деформирования основания. Отличие абсолютных пределов сопротивлений материалов (пропорциональности, упругости, текучести, прочности) от критических нагрузок на основание состоит в том, что первые являются мерой предельных напряжений, а нагрузки Н.М. Герсеванова представляют собой меру давления на полупространство.

Предельные давления, определяемые разными методами, можно отложить на оси абсцисс (давлений) графика Н.М. Герсеванова. В этом случае предельные давления располагаются в стадии сдвигов, а по их местоположению относительно давлений Герсеванова можно судить о том, к какой критической нагрузке анализируемое решение оказывается ближе.

208

Нормативные документы РФ регламентируют сравнительно небольшие предельные значения неровностей, формирующихся на покрытия в продольном и поперечном направлениях проезжей части. Поэтому грунты земляного полотна и дискретные материалы конструктивных слоев дорожной одежды должны работать преимущественно в стадии уплотнения. Добиться такой работы грунта или дискретного материала можно, связав деформацию в точке среды с ее осадкой. Решению этой задачи может способствовать предлагаемое уравнение предельного равновесия (4.55), в котором параметр d связан с деформацией, выраженной в долях от предельной деформации критерия Кулона – Мора. Подставив в уравнение (4.55) эмпирическую зависимость (4.65), получим условиепластичности, которое в явном виде связаносдеформацией.Это условиепластичности имеет вид

											1					1	2
											1					1
						1,3689												0,1807
	σ1 1 sin					1,3689						0,6882						0,1807
	σ1 1 sin				Ν				1с				1с
									1с				1с

		2
		2		1 sin	Ν
								1						1	2
					1,3689			1						1			0,1807

σ3			1 sin Ν							0,6882
σ3			1 sin Ν				1с					1с
							1с					1с						сΝ .	(4.91)

2				1 sin Ν
2				1 sin Ν

Зависимость (4.91) по величине отношения деформаций 1/ 1с имеет граничные условия 0,5 1/ 1с 1, обуславливающие граничные условия параметра d в уравнении предельного состояния (4.55) 0,33 d 0,5. В более краткой форме записи уравнения (4.55) условие пластичности запишем в виде

1 sin Ν

σ1

σ3

сΝ kд ,

(4.92)

1 sin Ν

где kд – коэффициент, принимаемый в соответствии с указаниями норматива [46, п. 3.35] для учета особенностей работы конструкции на границе песчаного слоя с нижним слоем несущего основания.

Во второй главе нами показано, что в сечении по оси симметрии нагрузки главные напряжения, возникающие от временной нагрузки, можно представить в общем виде

1 р К ; 3 1 р К . (4.93)

Величина коэффициента может быть определена по формуле (2.15) или (2.20). При расчете функции по выражению (2.15) минимальное главное напряжение имеет меньшее значение по сравнению с

209

величиной, рассчитанной при вычислении коэффициента по зависимости (2.20). Применение формулы (2.15) позволяет проектировать конструкцию с некоторым запасом. Подставив зависимость (2.15) в формулы (4.93), получим

1 р К ; 3 р К 1 1 K2 . (4.94)

Формулы (4.94) и условие пластичности (4.92) не учитывают составляющую напряжения от собственного веса грунта, расположенного выше наиболее опасной точки и веса дорожной одежды. Отметим, что в различных методах решения задачи о сопротивлении материала среды сдвигу влияние объемных сил может иметь различный качественный характер. Расчет главных напряжений в методах линейно деформируемого полупространства выполняют с применением принципа суперпозиции силы, то есть напряжения от фундаментной нагрузки и собственного веса грунта суммируются.

В дорожной конструкции слои, расположенные выше рассчитываемого элемента, перераспределяют давление от колеса на поверхность этого элемента. Поэтому рассчитываемый слой дорожной одежды или земляное полотно, хотя и располагается на некоторой глубине, не может быть отнесено к заглубленным конструкциям. Поэтому к таким слоям и земляному полотну понятие бытового давления не применимо. Из этого следует, что величина главных напряжений в наиболее опасной точке определяется суммой трех составляющих:

–главными напряжениями от транспортной нагрузки;

–главными напряжениями от собственного веса слоев дорожной конструкции, расположенной над рассчитываемым слоем;

–главными напряжениями от собственного веса земляного полотна грунта или материала проверяемого конструктивного слоя, расположенного выше наиболее опасной точки.

Поэтому максимальное главное напряжение в наиболее опасной точке проверяемого элемента дорожной конструкции может быть определено по формуле

n
1 р Коп i hi i 1 zоп ,	(4.95)
i 1

где Коп – величина коэффициента затухания максимального главного напряжения в наиболее опасной точке в сечении, расположенном по оси симметрии нагрузки; i и п – номер и общее количество слоев, расположенных выше рассматриваемого элемента конструкции с номером i+1; i и i+1 – соответственно объемный вес материалов i-го слоя и рассматриваемого элемента с номером i+1, Н/м3 (если р в Па); hi – толщина i-го слоя, м; zоп – расстояние от поверхности проверяемого элемента дорожной конструкции до наиболее опасной точки, м.

210

Применяя зависимость (2.5) при подстановке в нее = оп для расчета минимальных главных напряжений, получим выражение

р К

(4.96)

оп

i 1

оп

i 1

Зависимости (4.95) и (4.96) постулируют увеличение величины напряжений за счет влияния объемных сил от собственного веса слоев дорожной одежды, расположенных выше рассчитываемого элемента, и собственного веса материала, проверяемого на сдвиг слоя, расположенного над наиболее опасной точкой. Подставив зависимости (4.95) и (4.96) в уравнение (4.92), получим формулу для расчета безопасного давления

ihi

2с

Νk

1 sin

i 1

оп

. (4.97)

рб

Коп

1 sin

оп

1 sin

Коп

Зависимость (4.97) постулирует, что в результате действия объемных сил от части конструкции, расположенной выше наиболее опасной точки проверяемого на сдвиг элемента, величина безопасного давления уменьшается.

Несмотря на, казалось бы, верное применение принципа суперпозиции сил в формулах (4.95) и (4.96) рассуждения о влиянии объемных сил можно построить несколько иным образом. Для этого необходимо задействовать один из постулатов линейной теории упругости, а именно допущение о начальном состоянии. В нашем случае принцип начального состояния заключается в том, что составляющие деформации от сил собственного веса исчерпываются после окончания строительства. Таким образом, деформации, возникшие от собственного веса части конструкции, расположенной над проверяемой точкой рассматриваемого элемента, можно не учитывать. В этом случае расчет следует производить только от приращения напряжения, которым является напряжение от транспортной нагрузки. Аналогичное допущение вводится при расчете по сопротивлению сдвигу. Необходимые нам приращения главных напряжений определяются по формулам

1 р Коп i hi i 1 zоп i hi i 1 zоп р К . (4.98)

i 1 i 1

рК

. (4.99)

оп

i 1

оп

i 1

оп

i 1

i i

i 1

i i

211

Применяя этот алгоритм рассуждений, нами из формул (4.95) и (4.96) получены зависимости (4.93) в виде выражений (4.98) и (4.99), определяющих величину приращений главных напряжений, влияющих на сопротивление сдвигу и величину деформации элемента дорожной конструкции. Подставив зависимости (4.93) или тождественные им выражения (4.98) и (4.99) в условие пластичности (4.92), формулу для расчета безопасных давлений получим в виде

2 сΝ kд

1 sin

рб

оп

. (4.100)

1 sin

оп

Из (4.100) следует, что собственный вес материалов части дорожной конструкции не влияет на величину безопасных давлений, вследствие чего напряжения от собственного веса являются нейтральными по отношению к сдвигу.

Тем не менее в механике грунтов существует диаметрально противоположное мнение, согласно которому механизм сопротивления грунтов сдвигу по фиксированной плоскости обусловлен, в том числе и трением на контактах частиц грунта [49, c. 35]. Трение на контактах возникает как от временной транспортной нагрузки (или постоянной нагрузки от фундамента), так и собственного веса грунта. Эффект возникновения трения от транспортной нагрузки в зависимостях (4.97) и (4.100) учитывается, а трение от собственного веса грунта в этих формулах не учтено. Более того, в формуле (4.97) собственный вес грунта не только не способствует трению, но, наоборот, отрицательно влияет на сопротивление сдвигу. Поэтому с позиций механики грунтов зависимость (4.100) более точно отражает механизм сопротивления грунта сдвигу. Учитывая влияние собственного веса грунта на трение, возникающее по контактам частиц, условие пластичности (4.92) запишем в виде

1 sin Ν

σ1

σ3

пр,

(4.101)

1 sin Ν

где Тпр – предельное сопротивление сдвигу в наиболее опасной точке, Па.

Величина предельного сопротивления сдвигу может быть определена аналогично формуле нормативного документа [46, п. 3.35], но с поправкой на то, что наиболее опасная точка расположена не на поверхности слоя или земляного полотна, а на некотором расстоянии от нее.

212

n	tg 1,	(4.102)
Тпр сΝ kд i hi i 1 zоп
i 1

где 1 – угол внутреннего трения при однократно прикладываемой нагрузке, о.

					n
	2 сΝ kд i hi i 1 zоп									tg 1
рб					i 1
рб						Коп			d 1
						Коп
		1 sin	Ν	d			1 sin	Ν
		1 sin	Ν		оп		1 sin	Ν		.	(4.103)
		1 sin			оп		1 sin			.	(4.103)
		1 sin					1 sin
			Ν					Ν

Формула (4.103) представляет собой третий вариант расчета безопасного давления, в котором напряжения от собственного веса способствуют повышению трения на контактах частиц грунта. Следует обратить внимание на то, что в зависимости (4.103), так же, как и в нормативном методе расчета, углы внутреннего трения ϕ1 и ϕN неравны друг другу или, точнее, ϕ1ϕ>N. Это значит, что данные углы взяты в двух разных точках различных групп предельных кругов Мора или, как еще говорят, на разных площадках. Вследствие этого нормативный метод расчета так же, как и формулу (4.103), нельзя считать математически обоснованной. Поэтому, по нашему мнению, формула (4.103) может быть применена только потому, что при проектировании дорожных одежд в РФ применяется нормативный метод [46], несмотря на то, что в нем ϕ1ϕ>N.

Если принять формулу (4.103) со всеми ее недостатками, то можно убедиться, что зависимости (4.97), (4.100) и (4.103) представляют собой три варианта влияния собственного веса материала части среды, расположенной над наиболее опасной точкой, на сопротивление сдвигу. Каждая из этих формул соответствует определенным принципам механики сплошной среды и механики грунтов.

Взависимости (4.97) для расчета главных напряжений применен принцип суперпозиции сил, в результате чего напряжения от временной нагрузки и собственного веса суммируются. После переноса из левой части в правую напряжения от собственного веса меняют знак

иуменьшают величину безопасного давления.

Вформуле (4.103) учитывается влияние собственного веса грунта на повышение трения между контактами частиц, что соответствует принципам механики грунтов. При этом в (4.103) реализуется расчетная схема ОДН 218.046-01, согласно которой при расчете активного

213

касательного напряжения во внимание принимают только временную нагрузку, а объемные силы в виде собственного веса не учитывают. Формула (4.100) дает промежуточные результаты, в ней принимаются во внимание только напряжения от временной нагрузки. Это связано с тем, что данные напряжения являются приращением к уже существующим в среде напряжениям от собственного веса, которые вычисляются по зависимостям (4.98) и (4,99) и не вызывают существенных деформаций.

Ввыражениях (4.98) и (4.99) используется принцип учета влияния бытового давления при расчете осадок фундаментов. При таком расчете определяют напряжения от фундамента с учетом его веса, а вес вынутого из котлована грунта, называемый бытовым давлением, из действующей нагрузки вычитается. Следовательно, считается, что от веса изъятого грунта осадки стабилизировались, а часть внешней нагрузки всего лишь компенсирует вынутый грунт.

Отсюда следует, что все формулы (4.97), (4.100) и (4.103) исходят из определенной логики, базирующейся на разных физических моделях (расчетных схемах). Причем идеи, положенные в основу зависимостей (4.97) и (4.103), можно объединить, применяя условие пластичности в форме уравнения (4.101) с расчетом предельного сопротивления сдвигу по зависимости (4.102), а расчет главных напряжений производить по формулам (4.95) и (4.96).

Вэтом случае безопасное давление определяется по формуле

i 1

оп

рб

i 1

Коп

d 1

1 sin

i hi

i 1 zоп

оп

i 1

. (4.104)

1 sin

оп

В формуле (4.104) собственный вес материала, расположенного выше наиболее опасной точки, оказывает влияние на сопротивление сдвигу, но не столь значительное, как в зависимостях (4.97) и (4.103). Отметим, что в зависимости (4.104) так же, как в нормативном методе расчета и зависимости (4.103), имеет место 1> N.

Подобная дискуссия о количественном влиянии собственного веса грунта на величину предельного давления ведется в методах предельного равновесия грунта. К.В. Королев получил строгое математи-

214

ческое решение при допущении о малом влиянии собственного веса грунта [29].

Отметим, что рассчитывая осадки от давления, равного безопасной величине, определяемой, например, по формуле (4.103), их можно сопоставить с предельными значениями допускаемых деформаций земляного полотна. Сопоставление результатов расчета осадок с данными эксперимента позволит установить значения параметра d. Это позволяет связать допустимые осадки земляного полотна с отношением деформаций 1/ 1с. Кроме того, появляется возможность подобрать одну из модифицированных в гл. 2 моделей для расчета главных напряжений, которая наилучшим образом соответствует данным эксперимента.

В основе формулы (4.100) лежит условие пластичности (4.55), в котором касательные напряжения определяются по формуле

1	1		sin d	1		sin d
	σ						σ	.	(4.105)

2	1	1	sin		1	sin		3

Подставив в зависимость (4.105) формулу (2.5) и вынеся 1 за скобки, получим

		1 sin d	1		sin d
	1					.	(4.106)

2		1 sin		1	sin

Определяя максимальное главное напряжение произведением давления на коэффициент затухания К и рассчитывая функцию по выражению (2.15), получим формулу для расчета касательных напряжений в сечении по оси симметрии нагрузки

р К	1	sin d			1		sin d

			1	1 K2				. (4.107)

2	1	sin				1	sin

Подставляя в (4.107) формулы для определения коэффициента бокового давления в твердом теле и сыпучей среде, получим:

– для глинистых грунтов

р К	1 sin d				1		sin d

			1	1 K2				; (4.108)

2	1 sin	1				1	sin

– для песчаных грунтов при расчете по формуле Ж Биареза

(2.78):

215

р К	1	sin d			1 sin	1		sin d
			1	1 K2
									; (4.109)

2	1	sin			1 sin		1	sin

– для песчаных грунтов при расчете по формуле Ж Биареза

(2.79):

			р К			1	sin d

				2
				2		1	sin			sin d
р К				2				1 sin	1
р К				2				1 sin	1
	1	1 K2 1			sin						. (4.110)
2	1	1 K2 1		3	sin				1		. (4.110)
2				3				1 sin	1	sin

Функция может быть определена по формуле (2.20), представляющей собой функцию глубины и коэффициента Пуассона. В этом случае коэффициент Пуассона для песчаных моделей может быть рассчитан по формуле

	.	(4.111)

1

Подставив (4.111) в зависимость (2.20), получим

	1 K	2	1
1					.	(4.112)

	2
				1

Подстановкой (2.20) в (4.106) получим формулу для касательных напряжений в глинистых грунтах

рК	1 sin d					1	1		sin d
				2
		1	1 K		1					.(4.113)

2	1 sin					2		1	sin

Подстановкой (4.12) в (4.106) получим формулу для касательных напряжений в песчаных грунтах

	рК	1 sin d		1 K2			1		sin d
			1		1					.(4.114)

2		1 sin		2				1	sin
						1

Таким образом, при расчете касательных напряжений возникают различные варианты. Выше мы сравнивали зависимости (2.15) и (2.20) и отметили, что по формуле (2.15) значения коэффициента меньше, чем по зависимости (2.20) (см. рис. 2.2). Следовательно, минимальные главные напряжения, вычисленные по формуле (2.5) с привлечением зависимости (2.15), получатся меньше, чем рассчитанные по формуле (2.5) с привлечением выражения (2.20). Таким обра-

216

зом, расчет функции по формуле (2.15) приводит к более высоким значениям касательных напряжений, чем при вычислении этой функции по формуле (2.20). Также отметим, что в верхней части полупространства при относительных глубинах z/D<0,2 расхождения результатов расчета по формулам (2.15) и (2.20) не превышают 20 %. Поэтому для некоторых модифицированных моделей расчета главных напряжений расстояние от поверхности до наиболее опасной точки находится в пределах 0<zоп/D<0,2.

Применение зависимости (2.15) для расчета функции позволяет получить некоторый запас по сопротивлению сдвигу по сравнению с расчетом этого коэффициента по формуле (2.20). Окончательное суждение о применении (2.15) или (2.20) можно сформировать только на основе сопоставления данных расчета и эксперимента.

Еще одной особенностью предлагаемой модификации расчета дорожной конструкции по сопротивлению сдвигу является местоположение наиболее опасной точки. Расчеты касательных напряжений на октаэдрических площадках и площадках, повернутых к главным осям под углом 45 о, показали, что расстояние от поверхности до наиболее опасной точки различно при использовании разных модифицированных моделей расчета главных напряжений. Причем при расчете главных напряжений по одной и той же модели, включающей параметр материала, расстояние до наиболее опасной точки зависит от этого параметра.

На рис. 4.22 – 4.27 приведены зависимости касательных напряжений, вычисленных по формуле (4.107) при двух разных значениях параметра d 0,5 и 0,4. Для расчета главных напряжений применена модифицированная модель Лява – Фрелиха – Олсона (2.41) и (2.42), в соответствии с которой коэффициент затухания максимального главного напряжения в сечении по оси симметрии нагрузки определяется второй зависимостью (2.41). При расчете коэффициента затухания максимального главного напряжения в сечении по оси симметрии нагрузки принято три разных значения параметра Фрелиха n=1, n=3 и n=5. Отметим, что при n=3 зависимость Лява – Фрелиха – Олсона (2.41) дает тождественные результаты оригинальной формуле Лява (табл. 1.1), а касательные напряжения, вычисленные по выражению (4.107) при d=0,5, равны касательным напряжениям Кулона – Мора.

217

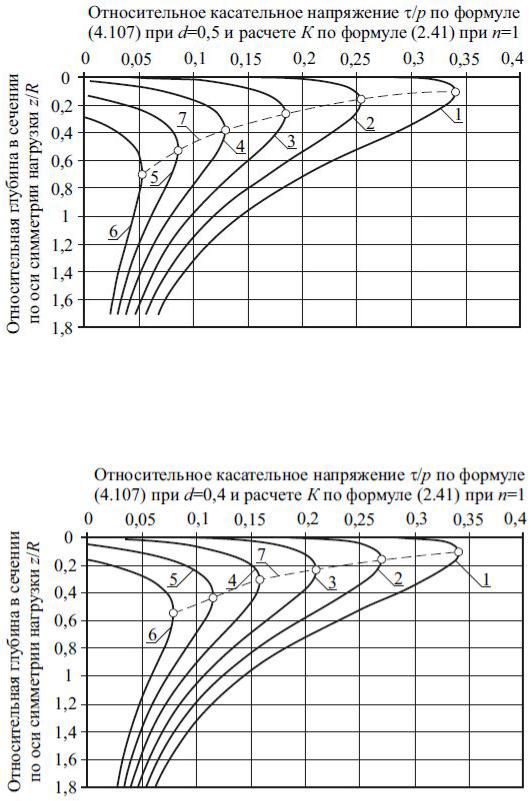
Рис. 4.22. Зависимость относительной величины касательных напряжений /р, вычисляемых по формуле (4.107) при d=0,5 и расчете коэффициента К по формуле (2.41) при п=1, от относительной глубины z/R и угла внутреннего трения : 1 – 6 при угле внутреннего трения 0; 10; 20; 30; 40 и 50 о; 7 – линия местоположения наиболее опасных точек

Рис. 4.23. Зависимость относительной величины касательных напряжений /р, вычисляемых по формуле (4.107) при d=0,4 и расчете коэффициента К по формуле (2.41) при п=1, от относительной глубины z/R и угла внутреннего трения : 1 – 6 при угле внутреннего трения 0; 10; 20; 30; 40 и 50 о; 7 – линия местоположения наиболее опасных точек

218

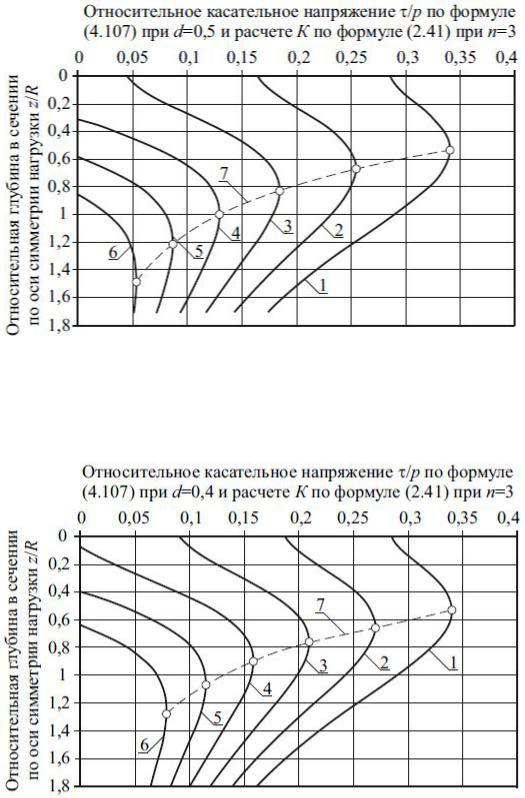
Рис. 4.24. Зависимость относительной величины касательных напряжений /р, вычисляемых по формуле (4.107) при d=0,5 и расчете коэффициента К по формуле (2.41) при п=3, от относительной глубины z/R и угла внутреннего трения : 1 – 6 при угле внутреннего трения 0; 10; 20; 30; 40 и 50 о; 7 – линия местоположения наиболее опасных точек

Рис. 4.25. Зависимость относительной величины касательных напряжений /р, вычисляемых по формуле (4.107) при d=0,4 и расчете коэффициента К по формуле (2.41) при п=3, от относительной глубины z/R и угла внутреннего трения : 1 – 6 при угле внутреннего трения 0; 10; 20; 30; 40 и 50 о; 7 – линия местоположения наиболее опасных точек

219

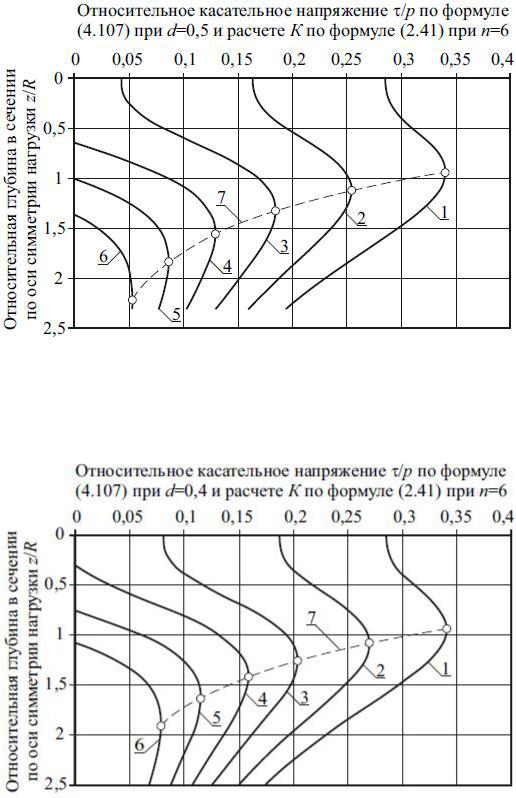
Рис. 4.26. Зависимость относительной величины касательных напряжений /р, вычисляемых по формуле (4.107) при d=0,5 и расчете коэффициента К по формуле (2.41) при п=6, от относительной глубины z/R и угла внутреннего трения : 1 – 6 при угле внутреннего трения 0; 10; 20; 30; 40 и 50 о; 7 – линия местоположения наиболее опасных точек

Рис. 4.27. Зависимость относительной величины касательных напряжений /р, вычисляемых по формуле (4.107) при d=0,4 и расчете коэффициента К по формуле (2.41) при п=6, от относительной глубины z/R и угла внутреннего трения : 1 – 6 при угле внутреннего трения 0; 10; 20; 30; 40 и 50 о; 7 – линия местоположения наиболее опасных точек

220

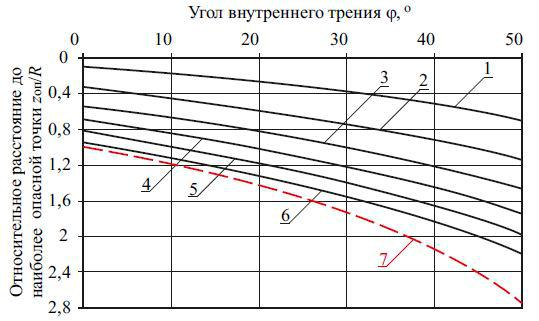
Из рис. 4.22 – 4.27 следует, что величина параметра d оказывает влияние на глубину расположения наиболее опасной точки и величину касательного напряжения в ней. Параметр Фрелиха n влияет на величину главных напряжений и приводит к изменению формы эпюры касательных напряжений, что приводит к изменению местоположения наиболее опасной точки, а величина касательного напряжения в этой точке при одинаковых параметрах d практически не изменяется. Глубина расположения наиболее опасной точки в наибольшей степени зависит от величины параметра Фрелиха, а значение касательного напряжения в этой точке обусловлено значением предлагаемого нами параметра d. Из этого диаметрально противоположного влияния параметров d и n на величину касательных напряжений в наиболее опасной точке и ее местоположение по глубине следует, что эти параметры дополняют друг друга.

На рис. 4.28 и 4.29 приведены относительные глубины расположения наиболее опасной точки в сечении по оси симметрии нагрузки, вычисленные из уравнения (4.107) для d=0,5 и d=0,4 при расчете главных напряжений по модифицированной модели Лява – Фрелиха – Олсона (кривые 1 – 6).

Рис. 4.28. Зависимость относительной глубины расположения наиболее опасной точки с касательным напряжением, определяемым по формуле (4.107) при d=0,5, от угла внутреннего трения: 1–6 – расчет коэффициента К выполнен по формуле (2.41) при n, равном 1; 2; 3; 4; 5 и 6; 7 – относительная максимальная глубина распространения неустойчивой области, вычисленная по приближенной формуле Г.В. Долгих

221

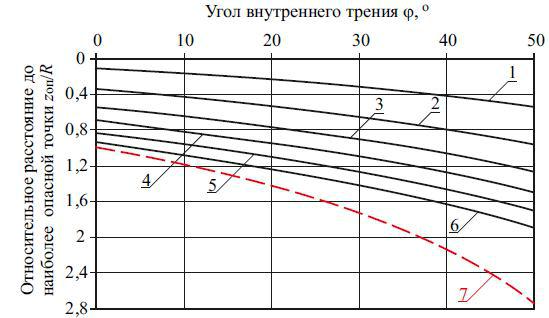
Рис. 4.29. Зависимость относительной глубины расположения наиболее опасной точки с касательным напряжением, определяемым по формуле (4.107) при d=0,4, от угла внутреннего трения: 1 – 6 – расчет коэффициента К выполнен по формуле (2.41) при n, равном 1; 2; 3; 4; 5 и 6; 7 – относительная максимальная глубина распространения неустойчивой области, вычисленная по приближенной формуле Г.В. Долгих

Также на рис. 4.28 и 4.29 приведены результаты расчета по приближенной формуле, определяющей местоположение нижней границы неустойчивой области, предложенной Г.В. Долгих (кривая 7). Из анализа данных рис. 4.28 и 4.29 следует разница между глубиной расположения наиболее опасной точки и максимальной глубиной распространения неустойчивой области, вычисленной по приближению Г.В. Долгих, которое имеет вид

max

;

max

(4.115)

D 2

где D – диаметр площадки, по которой распределена нагрузка по поверхности земляного полотна, м.

В данном случае максимальная глубина распространения неустойчивой области определяет точку, ограничивающую снизу в сечении по оси симметрии нагрузки некоторую область грунта, в которой напряжения выше предельных значений условия пластичности, положенного в основу расчета. Таким образом, если в точке, ограничивающей неустойчивую область грунта, имеет место предельное состояние и деформации сдвига отсутствуют, то внутри этой области

222

имеют место деформации сдвига. В этом случае наряду с оценкой сопротивления сдвигу земляное полотно и конструктивные слои дорожной одежды необходимо проверять по деформациям.

Отметим, что (4.115) определяет положение нижней границы зоны распространения неустойчивой области. В связи с тем, что эпюра касательных напряжений, построенная для сечения по оси симметрии нагрузки, имеет максимум на некоторой глубине от поверхности, то зона распространения неустойчивых областей должна иметь как нижнюю, так и верхнюю границы. Верхняя граница неустойчивой области может не совпадать с поверхностью слоя или земляного полотна, то есть располагаться ниже и иметь ординату меньше ноля.

В формулах (4.105) – (4.107) расчет главных напряжений и коэффициента затухания максимального главного напряжения можно выполнить по другим модифицированным нами моделям. В этом случае результаты расчета касательных напряжений и местоположения наиболее опасных точек будут отличаться от представленных нами на рис. 4.22 –4.29.

Для расчета величины безопасных давлений следует применять одну из формул (4.97), (4.100), (4.103) или (4.104). Выбор формулы должен определяться расчетной схемой учета собственного веса слоев дорожной одежды, расположенных выше проверяемого слоя и материала этого слоя, находящегося выше наиболее опасной точки.

4.6.Сопоставление результатов расчета безопасных давлений

сданными экспериментов по вдавливанию штампа в земляное полотно и щебеночное основание

Выше показано, что при расчете по сопротивлению сдвигу возможно применение достаточно большого количества модифицированных моделей для расчета главных напряжений. Также возможна вариация параметра d в условии пластичности. Поэтому для обоснованного выбора модели расчета главных напряжений и калибровки величины параметры d результатов расчета безопасных давлений необходимо сопоставлять с данными эксперимента.

Экспериментальные исследования выполнены путем штамповых испытаний земляного полотна автомобильной дороги Петровка – Калиновка. На рис. 4.30 приведен общий вид экспериментального участка, а на рис. 4.30 представлена установка, применяемая при испытаниях.

223

Рис. 4.30. Общий вид земляного полот-	Рис. 4.31. Общий вид земляного по-
на дороги Петровка – Калиновка	лотна дороги Петровка – Калиновка

Цель испытаний заключалась в определении величины безопасного давления. Под этой величиной понимается давление, при котором наблюдается переход от линейных осадок (стадия уплотнения) к нелинейным деформациям (стадия сдвигов).

В состав установки входят: жесткий круглый штамп, диаметром 37 см, реперная балка, к которой крепятся два индикатора часового типа ИЧ-100, фиксирующих осадку штампа, гидравлический домкрат с нагрузкой 5 т и ДОСМ, снабженный индикатором для определения усилия, сообщаемого штампом. На рис. 4.32 и 4.33 приведены детали крепления и вывода индикаторов к ДОСМ и штампу.

Рис. 4.32. Деталь измерения нагрузки	Рис. 4.33. Деталь измерения осадки
по индикатору ИЧ-100 с ДОСМ	правого края штампа по индикатору
	ИЧ-100

На рис. 4.34 приведены результаты штамповых испытаний и определение экспериментального значения безопасного давления.

224

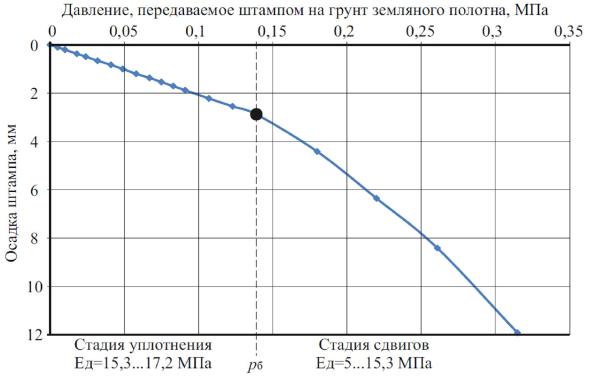
Рис. 4.34. Зависимость осадки круглого штампа от давления и определение безопасного давления

По завершении штамповых испытаний из грунтового массива отбирались пробы для определения параметров с и при трехосных испытаниях, выполненных при помощи АСИС-1. Результаты определения параметров грунта и безопасных давлений приведены в табл. 4.22.

Таблица 4.22. Результаты экспериментального определения безопасных

давлений

№ испытания	Параметры грунта		Безопасное давление, МПА
№ испытания	с, МПа	, град	Безопасное давление, МПА
	с, МПа	, град
1	0,022	29	0,139
2	0,024	27	0,139
3	0,020	29	0,124
4	0,025	26	0,139
5	0,020	26	0,124
6	0,021	25	0,124

Расчеты, выполненные по формулам (4.100) и (4.103) при параметре d, равном 0,3, 0,4 и 0,5, показали, что при расчете главных напряжений по любой из модифицированных моделей величина безо-

225

пасного давления меньше их экспериментальных значений на 30 – 60 %. Это позволяет сделать вывод, что полученное нами решение определяет величину абсолютно безопасного давления. Проектирование дорожных конструкций на такое абсолютно безопасное давление приведет к излишней материалоемкости. Вследствие этого расчет безопасного давления целесообразно производить из условия допущения возникновения в рассчитываемом элементе конструкции некоторой области, в которой предельное состояние по условию пластичности оказывается превзойдено.

Наиболее простым таким решением является формула, полученная автором совместно с Г.В. Долгих и А.Л. Калининым. В основу этой формулы положено условие пластичности Г.К. Арнольда (4.44). Полученная нами формула имеет вид

							1		1
	2 с		1	sin	1	sin		2	1
pб	2 с		1	sin	1	sin		1 K1
									, (4.116)
	K	1	1	sin	1	sin		1	, (4.116)
		1

где К1 – величина коэффициента затухания в точке, расположенной на нижней границе неустойчивой области (в этой точке имеет место предельное состояние по условию Г.К. Арнольда) сечения на оси симметрии нагрузки.

Кроме применения условия Г.К. Арнольда нами была рассмотрена возможность использования условия Кулона – Мора, из которого величина безопасного давления определяется по формуле


	1			2 c cos
pб	1			2 c cos				. (4.117)

	K
					1		1 sin
		1	1 sin			1 K12
		1	1 sin			1 K12
				1
				1

Положение нижней границы неустойчивой области по условиям пластичности Г.К. Арнольда и Кулона – Мора определяется в соответствии с предложением Г.В. Долгих по формулам (4.115). Таким образом, в зависимостях (4.116) и (4.117) предполагается, что предельное состояние по условиям пластичности Г.К. Арнольда и Кулона

–Мора может быть превзойдено в зоне, ограниченной снизу точкой, расположенной в сечении по оси симметрии нагрузки с ординатой, определяемой по формулам (4.115). В этой точке возникает предельное состояние по условию Г.К. Арнольда в формуле (4.116) и Кулона

–Мора в зависимости (4.117). По формулам (4.116) и (4.117) нами были вычислены безопасные давления, которые сравнивались с экс-

226

периментальными значениями. Вычисленные и измеренные экспериментальные безопасные давления приведены в табл. 4.23.

Таблица 4.23. Результаты определения безопасных давлений

с использованием модифицированной модели А. Лява или Лява – Фрелиха

– Олсона при n=3 и экспериментальные данные

	Параметры грун-			Безопасные давления, МПА
№ испы-		та				Расчет по формулам
№ испы-					(4.100)		(4.103)
тания	с, МПа		, град	Эксперимент	(4.100)		(4.103)	(4.116)	(4.117)
	с, МПа		, град		при		при	(4.116)	(4.117)
					d=0,5		d=0,5
1	0,022		29	0,139	0,1027		0,1113	0,133	0,226
2	0,024		27	0,139	0,1033		0,1103	0,138	0,207
3	0,020		29	0,124	0,0934		0,1019	0,121	0,206
4	0,025		26	0,139	0,1034		0,1096	0,140	0,225
5	0,020		26	0,124	0,0827		0,0889	0,112	0,180
6	0,021		25	0,124	0,0834		0,0890	0,115	0,181

Примечание. При расчете по формуле (4.103) принято 1= N, которые взяты по данным табл. 4.22 или 4.23.

Из анализа табл. 4.23 следует, что результаты расчета по формуле (4.116) в большей степени соответствуют экспериментальным данным. Однако если в формулах (4.100), (4.103) и (4.117) уменьшить ординату, ограничивающую неустойчивую область, то точность этих формул повысится. Тем не менее наиболее просто производить расчет безопасного давления по формуле (4.116), в которой коэффициент затухания максимального главного напряжения в сечении по оси симметрии нагрузки определяется по формуле (4.115).

Из выполненного сравнения данных эксперимента с результатами расчета следует, что для расчета величины безопасного давления может быть применено условие пластичности (4.55) при различных значениях параметра d, каждому из которых должна соответствовать своя ордината, расположенная в сечении по оси симметрии нагрузки и ограничивающая снизу неустойчивую область грунта.

При определении глубины распространения неустойчивой области по формулам (4.115) величину параметра d в формуле (4.103) можно принять в пределах 0,38 – 0,42, а в формуле (4.100) 0,28 – 0,33. Более подробные исследования по вопросу назначения максимальной глубины распространения неустойчивой области для различных условий пластичности, в том числе критерия (4.55), выполняет А.Л. Калинин.

227

Рис. 4.35. Фрезерование асфальтобетонного покрытия для подготовки площадки под штамповые испытания

Рис. 4.36. Монтаж штампа гидравлического и домкрата

Аналогичные штамповые испытания выполнены на щебеночном основании дорожной одежды ул. 21-я Амурская при ее реконструкции в 2013 г. Непосредственно перед выполнением испытания произведено фрезерование существующего покрытия (рис. 4.35). В результате чего подготавливалась площадка для выполнения штамповых испытаний.

На каждой подготовленной таким образом площадке производился монтаж установки для штамповых испытаний. При этом на поверхность щебеночного основания устанавливали круглый штамп, поверх которого ставили гидравлический домкрат (рис. 4.36).

Рис. 4.37. Монтаж и упор установки штамповых испытаний в самосвал

Поверх гидравлического домкрата монтировали ДОСМ, а установку для штамповых испытаний упирали в самосвал (рис. 4.37). Для измерения осадок применяли длиннобазовый прогибомер ПД 2,5 (рис. 4.38). Пяту щупа прогибомера размещали в специальном пространст-

228

ве домкрата так, чтобы она оказывалась как можно ближе к оси штампа (рис. 4.39).

Рис. 4.38. Установка прогибомера для	Рис. 4.39. Размещение пяты щупа про-
измерения осадки щебеночного осно-	гибомера на штампе и относительно
вания	домкрата

Нагрузка прикладывалась ступенями, что позволяло построить аналогичную показанной на рис. 4.34 зависимость осадки штампа от давления. Абсцисса точки перехода линейной зависимости в нелинейную принималась за безопасное давление.

После выполнения испытания производилась выемка щебня, после которой испытания повторялись на поверхности песка для определения модуля упругости подстилающего щебеночное основание полупространства.

Из щебня, взятого из основания, отбиралась проба массой 40 кг для определения зернового состава в лаборатории. По гранулометрическому составу определяли соответствие щебня виду, представленному в табл. 4.21, и назначали величину сцепления и угла внутреннего трения. Величину сцепления, соответствующую моменту испытания, рассчитывали по формуле (4.90) при N=106.

229

В результате установлено, что линейная зависимость осадки щебеночного основания от давления имеет место при давлениях, изменяющихся в диапазоне 0,37 – 0,44 МПа. Такие давления могут быть вычислены по формуле (4.103) для нижней точки слоя сечения по оси симметрии нагрузки, ордината которой вычисляется по формуле Н. Одемарка (2.31).

Из анализа экспериментальных данных следует, что давление от расчетной нагрузки р=0,6 МПа превышает безопасное давление на щебеночные и гравийные покрытия р=0,37 – 0,44 МПа, вследствие чего из зернистых материалов целесообразно устраивать слои основания дорожных одежд. При устройстве дорожных одежд с щебеночными или гравийными покрытиями их в обязательном порядке необходимо рассчитывать по критериям ровности.

4.7. Модифицированный метод расчета дорожной конструкции по сопротивлению сдвигу

При проектировании дорожных одежд сдвигоустойчивость грунтов земляного полотна обеспечивается недопущением возникновения касательных напряжений, превышающих предельное значение. В действующей нормативной [46, 47] инструкции критерий по условию сдвигоустойчивости подстилающего грунта и малосвязных конструктивных слоев дают в виде

Т	Т	пр	,	(4.118)

Кпр

где Кпр – требуемое минимальное значение коэффициента прочности, определяемое с учетом заданного уровня надежности; Т – расчетное активное напряжение сдвига (часть сдвигающего напряжения, непогашенная внутренним трением) в расчетной (наиболее опасной) точке конструкции от действующей временной нагрузки, определяемое из оригинального условия пластичности Кулона – Мора, Па; Тпр – предельная величина активного напряжения сдвига (в той же точке), превышение которой вызывает нарушение прочности на сдвиг, Па.

Предельное активное напряжение сдвига Тпр в грунте рабочего слоя (или в песчаном материале промежуточного слоя) определяют по формуле [46, 47]:

Тпр сN kд 0,1 ср zоп tg ст ,

(4.119)

где сN – сцепление в грунте земляного полотна (или в промежуточном песчаном слое), принимаемое с учетом повторности нагрузки, Па; kд – коэффициент, учи-

230

тывающий особенности работы конструкции на границе песчаного слоя с нижним слоем несущего основания; zоп – глубина расположения поверхности слоя, проверяемого на сдвигоустойчивость, от верха конструкции, см; ср – средневзвешенный удельный вес конструктивных слоев, расположенных выше проверяемого слоя, кг/см3; СТ – расчетная величина угла внутреннего трения материала проверяемого слоя при статическом действии нагрузки, град или рад соответственно.

При устройстве нижнего слоя из укрепленных материалов, а также при укладке на границе “основание – песчаный слой” разделяющей геотекстильной прослойки следует принимать значения kд рав-

ным [46, 47]:

–4,5 – при использовании в песчаном слое крупного песка;

–4,0 – при использовании в песчаном слое песка средней крупно-

сти;

–3,0 – при использовании в песчаном слое мелкого песка;

–1,0 – во всех остальных случаях.

В модифицированном расчете активное напряжение сдвига можно определить по обобщенной формуле:

Т kмм ном р,

(4.120)

где ном – удельное активное напряжение сдвига от единичной нагрузки, определяемое с помощью номограмм нормативных документов [46, 47]; р – расчетное давление от колеса на покрытие, Па; kмм – коэффициент, позволяющий выполнить пересчет активного напряжения сдвига, определяемого по оригинальному условию пластичности Кулона – Мора, на активное напряжение сдвига, вычисляемое по одному из модифицированных условий пластичности.

При использовании в качестве оригинального условия пластичности Кулона – Мора уравнения (4.43), а в качестве модифицированного критерия выражения (4.44) коэффициент kмм определяется отношением результатов расчета по левой части (4.44) к значениям, вычисленным по левой части (4.43). В данном случае коэффициент kмм находится по формуле

kмм	1 sin	.	(4.121)

	1 sin

Кроме модифицированной модели расчета активных напряжений сдвига для обеспечения сдвигоустойчивости дискретных материалов в дорожных конструкциях можно применять расчет по безопасным давлениям по критерию (4.1), который дадим в более общем виде

р	рб	,	(4.122)

i 1	Кпр

231

где pi+1 – давление на поверхности земляного полотна или слоя из дискретного материала, Па; рб – безопасное давление, Па; Кпр – требуемый коэффициент прочности дорожной одежды, принимаемый согласно указаниям ОДН

218.046.01.

Безопасное давление определяется по формуле (4.116), которую с учетом зависимости сцепления и угла внутреннего трения от числа расчетных нагрузок необходимо дать в виде

								1
						1 1	2	1
pб	1	2 сN	kд	1 sin N	1 sin N	1 1	K1
									. (4.123)
	K1			1 sin N	1 sin N	1
	K1			1 sin N	1 sin N	1

Безопасные давления по (4.123) можно определить с использованием любой модифицированной модели расчета главных напряжений. С учетом данных штамповых испытаний рекомендуем воспользоваться моделью А. Лява. Давление pi+1 может быть вычислено по формулам оригинальных моделей расчета напряжений при приведении пакета слоев, расположенных выше проверяемого слоя, к одному слою. В табл. 4.24 приведены формулы для расчета давления pi+1 по основным оригинальным моделям.

Таблица 4.24. Формулы

для расчета

давления,

передаваемого

на проверяемый слой

Автор модели

Формула для расчета давления pi+1

1,5

1 1

А. Ляв

i 1

М.И. Якунин

рi 1 р0

1 а

Еосн

р D

И.И. Кандауров

рi 1 р0

1 exp

М.П. Болштянский

рi 1 р0

1 2,25 Н D 2

Общепринятая модель распре-

2 Н

деляющей способности

i 1

232

Окончание табл. 4.24

2 Н

В.Н. Гусев

рi 1

р0

где Н – суммарная толщина слоев, расположенных выше проверяемого слоя, м; Е1 – модуль упругости верхнего слоя модели, вычисляемый как средневзвешенное по глубине значение, Па; D – диаметр отпечатка колеса на покрытии, м; α 1 – угол рассеивания напряжений верхнего слоя модели, вычисляемый как средневзвешенное по глубине значение, град или рад соответственно

Из анализа формул табл. 4.24 следует, что жесткость пакета слоев, расположенных выше проверяемого полупространства или промежуточного слоя, учитывается только в формуле М.И. Якунина и в формуле общепринятой модели распределяющей способности.

Поэтому для расчета давлений необходимо использовать одну из этих формул. В связи с обширной нормативной базой, содержащей модули упругости большого количества материалов, предпочтение можно отдать формуле М.И. Якунина. Кроме того, для определения давления pi+1 можно применять метод Н. Одемарка.

Выводы по главе 4

1. Разработан способ модификации оригинальных условий пластичности, состоящий в том, что:

–принимаются два оригинальных критерия, предельные поверхности которых ограничивают область варьирования поверхности разрушения модифицированного критерия. Одним из этих условий является критерий Кулона – Мора, предельная поверхность которого должна ограничивать диапазон варьирования поверхностей разрушения сверху;

–подбираются формулы, описывающие связь пределов прочно-

сти на сжатие и растяжение с параметрами предельной прямой с и и третьим параметром d. Подбор формул выполняют так, чтобы при d=0,5 эти зависимости преобразовывались к (4.3) и (4.13), а при d=0 определяли связь пределов прочности с параметрами оригинального критерия, который ограничивает модифицированное условие снизу. В предлагаемом модифицированном критерии таким условием является третья теория прочности.

2. Ввод третьего параметра в условие Кулона – Мора позволяет учитывать величину предельных деформаций, при возникновении ко-

233

торых наступает предельное состояние по модифицированному условию пластичности.

3. Экспериментами по трехосному сжатию суглинка легкого установлено, что:

–появление площадок скольжения соответствует отношению осевой деформации 1 к предельной для условия Кулона – Мора деформации 1с равному 1/ 1с=0,5. Это отношение определяет нижнюю границу варьирования параметра d=0,3;

–прогрессирование локализации деформаций вдоль площадок

скольжения имеет место при вариации отношения 1/ 1с в интервале 0,5…0,8. Такому интервалу соответствует варьирование параметра d

впределах 0,3 d 0,45;

–при 1/ 1с=0,8 процесс формирования площадок сдвига заканчивается, а величина d=0,45 является верхним пределом интервала варьирования введенного параметра.

4. Предложен критерий относительной устойчивости грунтовой среды – безопасное давление. Суть критерия состоит в том, что при передаче на земляное полотно давления, равного его безопасной величине в точке, ограничивающей снизу зону распространения неустойчивой области, возникает предельное состояние по условию пластичности, положенному в основу вывода формулы безопасных давлений.

5. Модифицированное условие Кулона – Мора (4.55) положено в основу расчетов по сопротивлению сдвигу. В этом случае после подстановки в уравнение (4.55) функций главных напряжений его левая часть определяет величину касательных напряжений. Кроме того, представив главные напряжения произведением давления и функции затухания напряжения по глубине, из уравнения (4.55) получим формулы для определения безопасного давления на грунт земляного полотна и песчаный дополнительный слой основания дорожной одежды.

6. Дана экспериментальная оценка безопасным давлениям, рассчитанным из условий пластичности Кулона – Мора и Г. Арнольда, а также нового мультиповерхностного критерия (4.55), включающего в себя третий параметр материала d.

7. Установлено, что если давление, передаваемое на земляное по-

лотно, равно безопасному давлению, рассчитанному из условия Г. Арнольда с ограничением неустойчивой зоны ординатой, определяемой по зависимости (4.115) и при вычислении главных напряже-

234

ний по модифицированной модели А. Лява, грунт работает в стадии уплотнения. При этом давления, равные безопасной величине, порождают вертикальные деформации в пределах международных допусков на ровность покрытия по IRI.

8.Для практического применения нами внесено два предложения. Первое заключается в том, чтобы при проектировании дорожных одежд сопротивление сдвигу грунтов земляного полотна проверялось по критерию безопасных давлений. Второе предложение состоит в совершенствовании нормативного метода расчета грунтов земляного полотна и песчаных слоев дорожной одежды. Суть модифицированного метода состоит в определении касательных напряжений из условия пластичности Г. Арнольда, а не Кулона – Мора, как это принято в настоящее время. Для облегчения расчетов получен коэффициент, представляющий собой отношение функций касательных напряжений по условиям Арнольда и Кулона – Мора. Произведение этого коэффициента и касательных напряжений, вычисленных по номограммам нормативных документов, позволяет определить касательные напряжения для условия пластичности Г. Арнольда.

9.Установлено, что при устройстве двухслойных асфальтобетонных покрытий суммарной толщиной от 12 см на щебеночное основание обеспечиваетсяпередачадавлений,непревышающихбезопасной величины.

5.ПРИМЕР ПРОЕКТИРОВАНИЯ ДОРОЖНЫХ ОДЕЖД ПО ПРЕДЛАГАЕМЫМ МЕТОДАМ

Вданной главе ставится цель сравнить результаты расчета дорожных одежд нежесткого типа по критериям прочности и сдвигоустойчивости, регламентируемым нормативными документами и предлагаемыми нами. Для этого выполним расчет дорожной одежды капитального типа для автомобильной дороги Петровка – Калиновка, расположенной в Омской области.

Пример 1. Техническая категория дороги III. Срок службы дорожной одежды 12 лет, в течение которого реализуется 500000 расчетных нагрузок. Предельный коэффициент разрушения 0,10 при заданной надежности 0,95. Требуемый коэффициент прочности при расчете составляет:

– по критерию упругого прогиба 1,17;

– по условию сдвигоустойчивости подстилающего грунта и малосвязных конструктивных слоев 1,0;

235

– на сопротивление монолитных слоев усталостному разрушению от растяжения при изгибе значение требуемого коэффициента прочности составляет 1,0.

В табл. 5.1 приведена конструкция дорожной одежды.

Таблица 5.1. Конструкция дорожной одежды №1 и показатели

механических свойств материалов

		Показатели механических свойств при расчете
		по уп-				на растяжение при из-
	Тол-	руго-	по устойчивости				гибе
	щина	му	по устойчивости
Материал слоя	щина	му	против сдвига
Материал слоя	слоя,	про-	против сдвига			Е,	R0,
	см	гибу				Е,	R0,	α	m
	см	гибу				МПа	МПа	α	m
		Е,	Е,	С,	,	МПа	МПа
		МПа	МПа	кПа	град
Плотный асфаль-
тобетон типа А из
горячей, мелко-	5	3200	1100	–	–	4500	9,8	5,9	5,5
зернистой смеси	5	3200	1100	–	–	4500	9,8	5,9	5,5
зернистой смеси
на битуме БНД
60/90
Пористый ас-
фальтобетон из
горячей, крупно-	7	2000	700	–	–	2800	8	7,1	4,3
зернистой смеси	7	2000	700	–	–	2800	8	7,1	4,3
зернистой смеси
на битуме БНД
60/90
Черный щебень,
уложенный по	10	600	600	–	–	600	–	–	–
способу заклинки
Щебеночно-	20	290	290	–	–	290	–	–	–
песчаная смесь С4	20	290	290	–	–	290	–	–	–
Песок средней	30	120	120	2,56	25,3	120	–	–	–
крупности	30	120	120	2,56	25,3	120	–	–	–
крупности
Суглинок легкий	–	44,6	44,6	7,98	6,66	44,6	–	–	–
Wрасч/Wт=0,68	–	44,6	44,6	7,98	6,66	44,6	–	–	–
Wрасч/Wт=0,68

Величина минимального требуемого общего модуля упругости конструкции вычислена по эмпирической формуле, регламентируемой [346]. Минимальный требуемый общий модуль составляет

Еmin 98,65 lg500000 3,55 212 МПа.

В соответствии с ОДН 218.046-01 при суммарном числе приложений нагрузки 500000 требуемый общий модуль упругости дорожной одежды должен быть не менее 220 МПа. Следовательно, Еmin

236

принимается 220 МПа. Расчетная нагрузка типа А1 характеризуется диаметром расчетного отпечатка шины D=37 см и давлением р=0,6 МПа.

В табл. 5.2 приведены результаты расчета дорожной одежды по допускаемому упругому прогибу.

Таблица 5.2. Результаты расчета дорожной одежды № 1 по допускаемому

упругому прогибу

Материал слоя		h, см	h/D	Ев, МПа	Ен/Ев	Еобщ/Ев	Еобщ, МПа
Суглинок легкий		–	–	44,6	–	–	44,6
Песок средней круп-		30	0,81	120	0,372	0,64	76,8
ности
Щебеночно-песчаная		20	0,54	290	0,265	0,44	127,6
смесь С4		20	0,54	290	0,265	0,44	127,6
смесь С4
Черный	щебень за-	10	0,27	600	0,213	0,294	176,4
клинкой
Пористый асфальтобе-		7	0,19	2000	0,088	0,124	248
тон
Плотный	асфальтобе-	5	0,135	3200	0,078	0,09	288
тон

Коэффициент прочности

288 Кпр 220 1,31.

Таким образом, фактический коэффициент прочности при расчете по допускаемому упругому прогибу превышает требуемое значение 1,31>1,17, следовательно, условие прочности выполнено.

При расчете нижнего слоя покрытия по критерию сопротивления усталостному растяжению от изгиба модуль упругости пакета слоев равен

	Е			4500 5		2800 7		3508 МПа.

		1	5			7
Тогда отношения Е1/Ен и h/D составят
	Е1		3508		19,9;		h		5 7	0,32.

	Ен						D
		176,4						37

В этом случае растягивающее напряжение от единичной нагрузки будет 2,4 МПа. Расчетное растягивающее напряжение

р 2,4 0,85 0,6 1,224 МПа.

Коэффициент k1, отражающий влияние на прочность усталостных процессов,

237

7,1

k1 4,3500000 0,336.

Отсюда прочность пористого асфальтобетона, используемого для устройства нижнего слоя покрытия при многократном растяжении при изгибе, составляет

RN 8 0,8 0,336 1 0,1 1,71 1,78 МПа.

Коэффициент прочности

1,78 Кпр 1,224 1,45.

Таким образом, фактический коэффициент прочности при расчете на сопротивление усталостному растяжению при изгибе превышает требуемое значение 1,45>1, следовательно, условие прочности выполнено.

При расчете по условию сдвигоустойчивости дополнительного слоя основания из песка средней крупности модуль упругости пакета слоев, расположенных выше проверяемого слоя,

Е1 1100 5 700 7 600 10 290 20 528,6 МПа. 5 7 10 20

Тогда отношения Е1/Ен и h/D

Е1		528,6	6,88;	h	42	1,14.

Ен	76,8			D 37

В этом случае удельное активное напряжение сдвига от единичной нагрузки, определяемое с помощью номограммы, будет 0,036 МПа. Следовательно, для оригинального условия Кулона – Мора активное напряжение сдвига в грунте земляного полотна

Т 0,6 0,036 0,022 МПа.

Средневзвешенный удельный вес конструктивных слоев, расположенных выше дополнительного слоя основания,

ср	0,0024 5 0,0023 7 0,002 10 0,002 20	0,0021 кг/см3.

	5 7 10 20

Расчетная величина угла внутреннего трения песка среднего при статическом действии нагрузки составляет 32 о.

Предельное активное напряжение сдвига Тпр в песчаном дополнительном слое основания

Тпр 0,00256 1 0,1 0,0021 5 7 10 20 tg32 0,0081 МПа.

238

Коэффициент прочности при расчете по условию сдвигоустойчивости в дополнительном слое основания с использованием оригинальной модели Кулона – Мора:

0,0081 Кпр 0,022 0,37.

Таким образом, критерий нормативного метода расчета не выполняется, а конструкция дорожной одежды нуждается в изменении.

В качестве мероприятий обеспечения сдвигоустойчивости дополнительного слоя основания можно предусмотреть:

1.Укладку на границе “основание из щебеночно-песчаной смеси С4

– дополнительный слой основания из песка среднего” разделяющей геотекстильной прослойки. В этом случае коэффициент kд увеличивается до 4, а следовательно, повышается предельное активное напряжение сдвига.

2.Укрепление щебеночно-песчаной смеси С4 вяжущим материалом. Это также позволяет увеличить коэффициент kд до 4. Кроме того, при увеличении модуля упругости верхнего слоя модели активное напряжение сдвига в проверяемом песчаном слое уменьшится.

3.Увеличение толщины верхнего слоя модели, способствующее снижению активного напряжения сдвига и увеличению величины предельного активного напряжения сдвига.

При укладке на границе раздела слоев из щебеночно-песчаной смеси С4 и песка средней крупности разделяющей геотекстильной прослойки величина предельного активного напряжения сдвига составит:

Тпр 0,00256 4 0,1 0,0021 5 7 10 20 tg32 0,00158 МПа.

В этом случае коэффициент прочности при расчете по условию сдвигоустойчивости в дополнительном слое основания из песка средней крупности по нормативному методу

0,0158 Кпр 0,022 0,73.

Условие сопротивления сдвигу не выполняется. Поэтому наряду с введением геосинтетической армирующей прослойки произведем увеличение толщины нижнего слоя основания из щебеночнопесчаной смеси С4 до 22 см.

Тогда средневзвешенный удельный вес конструктивных слоев, расположенных выше дополнительного слоя основания, и предельное активное напряжение сдвига Тпр в песке средней крупности

239

ср	0,0024 5 0,0023 7 0,002 10 0,002 22	0,0021 кг/см3.

	5 7 10 22

Тпр 0,00256 1 0,1 0,0021 5 7 10 22 tg32 0,001601 МПа.

Модуль упругости пакета слоев, расположенных выше проверяемого слоя,

Е1 1100 5 700 7 600 10 290 22 517,7 МПа. 5 7 10 22

Тогда отношения Е1/Ен и h/D

Е1		517,7	6,74;	h	44	1,19.

Ен
	76,8			D 37

Вэтом случае удельное активное напряжение сдвига от единичной нагрузки, определяемое с помощью номограммы, составляет 0,026 МПа. Следовательно, для оригинального условия Кулона – Мора активное напряжение сдвига в грунте земляного полотна

Т0,6 0,026 0,0156 МПа.

Вэтом случае коэффициент прочности при расчете по условию сдвигоустойчивости в дополнительном слое основания из песка средней крупности с использованием нормативного метода

0,016 Кпр 0,0156 1,03.

Условие сопротивления сдвигу в дополнительном слое основания выполнено.

При расчете по условию сдвигоустойчивости в грунте земляного полотна модуль упругости пакета слоев

Е1 1100 5 700 7 600 10 290 22 120 30 615,7 МПа. 5 7 10 22 30

Тогда отношения Е1/Ен и h/D составят

Е1		615,7	13,8;	h	74	2.

Ен	44,6			D 37

В этом случае удельное активное напряжение сдвига от единичной нагрузки, определяемое с помощью номограммы, будет 0,0153 МПа.

Следовательно, для оригинального условия Кулона – Мора активное напряжение сдвига в грунте земляного полотна

Т 0,6 0,0153 0,0092 МПа.

Средневзвешенный удельный вес конструктивных слоев, расположенных выше земляного полотна, кг/см3:

240

ср	0,0024 5 0,0023 7 0,002 10 0,002 22 0,00195 30	0,002.
	5 7 10 22 30

Расчетная величина угла внутреннего трения суглинка легкого при расчетной относительной влажности 0,68 и при статическом действии нагрузки составляет 19,2 о.

Предельное активное напряжение сдвига Тпр в грунте земляного полотна

Тпр 0,00798 1 0,1 0,002 5 7 10 22 30 tg19,2 0,0131 МПа.

Коэффициент прочности при расчете по условию сдвигоустойчивости в грунте земляного полотна с использованием оригинальной модели Кулона – Мора

0,0131 Кпр 0,0092 1,42.

Коэффициент прочности при расчете по условию сдвигоустройчивости в грунте земляного полотна с использованием оригинальной модели Кулона – Мора превышает требуемое значение 1,42>1, значит, условие прочности выполнено.

Следовательно, запроектированная конструкция удовлетворяет всем трем критериям прочности ОДН218.046-01.

Далее выполним проверку предлагаемых нами условий сопротивления сдвигу (4.120) и (4.121) в дополнительном слое основания и в грунте земляного полотна.

В соответствии с формулами (4.120) и (4.121) активное касательное напряжение в дополнительном слое основания

Т	1 sin25,3	0,026 0,6 0,0246 МПа.

1 sin25,3

Тогда коэффициент прочности

0,016 Кпр 0,0246 0,65.

Таким образом, условие сдвигоустойчивости в песчаном слое при использовании формул (4.120) и (4.121), позволяющих задействовать критерий Г.К. Арнольда, не выполняется. Значит, для обеспечения сдвигоустойчивости песчаного слоя введения геотекстильной прослойки не достаточно.

Поэтому увеличим толщину нижнего слоя основания из щебе- ночно-песчаной смеси С4 до 37 см. Модуль упругости пакета слоев

Е1 1100 5 700 7 900 10 290 37 459,8 МПа. 5 7 10 37

241

Отношения Е1/Ен и h/D

Е1		459,8	5,99;	h	59	1,59.

Ен
	76,8			D 37

В этом случае удельное активное напряжение сдвига от единичной нагрузки, определяемое с помощью номограммы [46], будет

0,0184 МПа.

Активное касательное напряжение в песчаном слое

Т	1 sin25,3	0,0184 0,6 0,0174 МПа.

1 sin25,3

Величина предельного активного напряжения сдвига

Тпр 0,00256 4 0,1 0,0021 5 7 10 37 tg32 0,0018 МПа.

Фактический коэффициент прочности

0,018 Кпр 0,0174 1,03.

Следовательно, условие сдвигоустойчивости выполняется.

По оригинальной модели М.И. Якунина давление, передаваемое на дополнительный слой основания, составит

					2 1
		0,59	3	459,8
р 0,6						0,064 МПа.
	1 1
		0,37		76,8

По формуле (4.115) относительная максимальная глубина распространения неустойчивых областей

Z	max	1		25,3 ,14
			tg		0,789.
		2		2 180
	D

При расчете песчаного слоя необходимо максимальную глубину неустойчивых областей сопоставить с толщиной песчаного слоя. Для этого по формуле А.В. Смирнова определяется диаметр площадки, по которой нагрузка распределена по поверхности проверяемого слоя.

D	0,37	0,6	1,133м.

i 1		0,064

Тогда относительная толщина песчаного слоя составит

h		0,30	0,265м.

Di 1 1,133

Отсюда следует, что относительная максимальная глубина распространения неустойчивых областей превышает относительную толщину песчаного слоя.

242

Значит, проверка по критерию безопасных давлений не производится.

Расчет грунта земляного полотна на сопротивление сдвигу начнем с проверки условия (4.118).

Модуль упругости пакета слоев, расположенных выше земляного полотна,

Е1 1100 5 700 7 600 10 290 37 120 30 314,9 МПа. 5 7 10 37 30

Тогда отношения Е1/Ен

Е1		314,9	7,06;	h	89	2,41.

Ен	44,6			D 37

Вэтом случае удельное активное напряжение сдвига от единичной нагрузки, определяемое с помощью номограммы, будет 0,0157 МПа.

Всоответствии с формулами (4.120) и (4.121) активное касательное напряжение в грунте земляного полотна

		Т	1 sin6,66	0,0157 0,6 0,0106 МПа.
		Т		0,0157 0,6 0,0106 МПа.
			1 sin6,66
Средневзвешенный удельный вес конструктивных слоев, распо-
ложенных выше земляного полотна, кг/см3:
	ср	0,0024 5 0,0023 7 0,002 10 0,002 37 0,00195 30
	ср		5 7 10 22 37
			5 7 10 22 37

0,00195 МПа.

Предельное активное напряжение сдвига Тпр в грунте земляного полотна, МПа:

Тпр 0,00798 1 0,1 0,00195 5 7 10 22 37 tg19,2 0,0138.

Коэффициент прочности при расчете по условию сдвигоустойчивости в грунте земляного полотна с использованием оригинальной модели Арнольда

0,0138 Кпр 0,0106 1,31.

Таким образом, условие прочности выполняется.

Произведем оценку сдвигоустойчивости грунта земляного полотна по критерию безопасных давлений, выражающемуся формулой

(2.62).

Для расчета давлений, передаваемых дорожной одеждой на земляное полотно, воспользуемся оригинальной моделью М.И. Якунина.

243

Для толщины пакета слоев, расположенных над земляным полотном, равным 89 см, модуль упругости равен 609,7 МПа. Следовательно, давление от дорожной одежды на грунт земляного полотна по оси симметрии нагрузки

					2 1
		0,89	3	314,9
р 0,6						0,0287 МПа.
	1 1
		0,37		44,6

По формуле (2.51) относительная максимальная глубина распространения неустойчивых областей

Z	max	1		,66 ,14
			tg		0,562.
		2		2 180
	D

Коэффициент затухания напряжения для относительной глубины 0,562 по оригинальной модели А. Лява

						1	1				2 1,5
		K	1	1 1									0,583.
		K		1 1									0,583.
						2		0,562
						2		0,562
Отсюда безопасное давление, МПа,
						pб	1
						pб
							0,583
							1							,35	1
												2			1
	0,884				0,884				1 0,583			2
	0,884				0,884				1 0,583
	2 0,00798 1				1,116					1 ,35						0,0314.
	1,116				1,116					1 ,35

Фактический коэффициент прочности при проверке сдвигостойчивости в грунте земляного полотна по безопасным давлениям с использованием оригинальной и модифицированной модели М.И. Якунина составляет

0,0314 Кпр 0,0287 1,09.

Условие прочности выполняется.

Отметим, что при расчете грунта земляного полотна коэффициент прочности по безопасным давлениям Кпр=1,09 меньше, чем при проверке по модифицированному условию сдвигоустойчивости Кпр=1,31. Это подтверждает то, что при расчете по критерию безопасных давлений жесткость дорожных одежд должна быть выше, чем при расчете по модифицированному, вводом зависимости (4.121) и, тем более, оригинальному условию сдвигоустойчивости.

244

В табл. 5.3 приведена конструкция дорожной одежды, удовлетворяющая нормативным критериям, регламентированным ОДН 218.04601 и критериям, предложенным нами.

Таблица 5.3. Конструкция дорожной одежды капитального типа

автомобильной дороги III технической категории «Петровка – Калиновка» (Омская область)

		Толщина слоя при расчете,
Конструктивный	Материал конструктивного		см
слой (элемент)	слоя	ОДН	предлагаемому
		218.046-01	методу
Верхний слой	Плотный асфальтобетон типа
Верхний слой	А из горячей, мелкозернистой	5	5
покрытия	А из горячей, мелкозернистой	5	5
покрытия	смеси на битуме БНД 60/90
	смеси на битуме БНД 60/90
Нижний слой по-	Пористый асфальтобетон из
Нижний слой по-	горячей, крупнозернистой	7	7
крытия	смеси на битуме БНД 60/90
	смеси на битуме БНД 60/90
Верхний слой	Черный щебень, уложенный	10	10
основания	по способу заклинки	10	10
основания	по способу заклинки
Нижний слой ос-	Щебеночно-песчаная смесь	22	37
нования	С4	22	37
нования	С4
	Материал, соответствующий
Геосинтетическая	требованиям ОДМ «Рекомен-
Геосинтетическая	дации по применению геосин-	–	–
армирующая	тетических материалов при	–	–
прослойка	тетических материалов при
прослойка	строительстве и ремонте ав-
	строительстве и ремонте ав-
	томобильных дорог»
Дополнительный	Песок средней крупности	30	30
слой основания
Грунт земляного	Суглинок легкий с расчетной	–	–
полотна	влажностью W/Wт=0,68	–	–
полотна	влажностью W/Wт=0,68

Для практического применения рекомендуемых нами критериев расчет можно производить в иной последовательности, сокращающей число исходов, при которых предлагаемые условия не выполняются, а конструкция дорожной одежды нуждается в изменениях и новом проектировании.

При наличии в конструкции дорожной одежды дополнительного слоя основания из песка рекомендуемая последовательность расчета включает в себя:

1.Конструирование дорожной одежды с назначением минимальных толщин слоев.

2.Проверку по сопротивлению сдвигу, используя условие (4.118) и

245

формулы (4.120) и (4.121). По результатам расчета устанавливается суммарная толщина пакета слоев, расположенных выше дополнительного слоя и каждого отдельного слоя в этом пакете.

3.Сопоставление величины максимальной относительной глубины распространения неустойчивых областей в дополнительном слое основания с относительной толщиной песка. При необходимости выполняется проверка сопротивления песка сдвигу по безопасным давлениям с использованием условия (4.122), формулы (4.116) при вычислении коэффициента К1 по модели А. Лява и модели М.И. Якунина. В случае необходимости производится корректировка толщины пакета слоев, расположенных над проверяемым слоем, и вновь проверяется критерий (4.122).

4.Проверку по сопротивлению сдвигу в грунте земляного полотна по безопасным давлениям с применением тех же формул. При необходимости толщина пакета слоев, расположенных выше земляного полотна, корректируется, а критерий (4.122) проверяется вновь.

5.Проверку по сопротивлению сдвигу в грунте земляного полотна, используя условие (4.118) и формул (4.116) и (4.115). При необходимости толщина слоев пакета, лежащего выше земляного полотна, корректируется, а условие (4.118) перепроверяется.

6.Проверку критериев прочности, регламентируемых ОДН 218.046-

01.При этом расчет по сопротивлению сдвига в дополнительном слое основания и грунте земляного полотна можно не выполнять. Связано это с тем, что коэффициент kмм принимает величину, равную единице только при нулевом значении угла внутреннего трения. Во всех других случаях kмм>1, поэтому активное напряжение сдвига по методу, предлагаемому нами, всегда больше, чем по нормативному методу.

Если в конструкции дорожной одежды пески не используются, то необходимость в их проверке по условиям сдвигоустойчивости отпадает, а из указанной последовательности пункты 2 и 3 исключаются.

246

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.202117.79 Mб22559.pdf
#
07.01.2021374.85 Кб3256.pdf
#
07.01.202117.98 Mб102560.pdf
#
07.01.202117.98 Mб542561.pdf
#
07.01.202118.09 Mб1862562.pdf
#
07.01.202118.1 Mб142563.pdf
#
07.01.202118.2 Mб362564.pdf
#
07.01.202118.65 Mб112565.pdf
#
07.01.202118.84 Mб362566.pdf
#
07.01.202119.12 Mб202567.pdf
#
07.01.202119.8 Mб492568.pdf