Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2563.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

18.1 Mб

Скачать

☆

<<< < Предыдущая 12 / 62 3 4 5 6 > Следующая >>>

2.2. Модификация моделей расчета главных напряжений

Предлагаемые нами формулы (2.5) и (2.23) позволяют модифицировать любую из известных моделей расчета главных напряжений, возникающих в сечении по оси симметрии нагрузки. Некоторые из рассматриваемых нами решений получены совместно с Н.П. Александровой и Г.В. Долгих в работе2.

Рассмотрим модификацию модели А. Лява, для выполнения которой формулу для расчета максимальных главных напряжений представим в виде

	1	р К ;					К 1					1			.					(2.24)
	1	р К ;					К 1							3	.					(2.24)
										1 R/z 2 2
Подставив (2.24) в формулу (2.15) и (2.23), получим

									1				2
									1
	1			1 1									.							(2.25)
	1			1 1							3		.							(2.25)
										2
										2
								1 R/z 2

																			2
				1										1
				1										1
2	3 р 1								1	1 1										. (2.26)
2	3 р 1					3			1	1 1								3		. (2.26)
					2											2
			1 R/z		2	2								1 R/z		2	2
			1 R/z			2								1 R/z			2

В	точке, расположенной				на				поверхности грунтового полупро-

странства в сечении по оси симметрии нагрузки, коэффициенты =1 и К=1, вследствие чего формулы (2.25) и (2.26) принимают вид

2 z 0 3 z 0 р .

(2.27)

Таким образом, предлагаемый способ расчета минимального главного напряжения приводит к тому, что в точке, расположенной по оси симметрии нагрузки, на поверхности полупространства возникает компрессионное сжатие, что соответствует экспериментальным данным. В точке, расположенной на бесконечности, значения коэффициентов и К принимают нулевое значение. В этой точке сечения по оси симметрии нагрузки грунт работает в условиях одноосного сжатия. Во всех остальных точках рассматриваемого сечения величина трех главных напряжений положительна, вследствие чего грунт полу-

2 Александров А.С., Александрова Н.П., Долгих Г.В. Модифицированные модели для расчета главных напряжений в дорожных конструкциях из дискретных материалов //Строительные материалы. – 2012. – № 10. – С. 14 – 17.

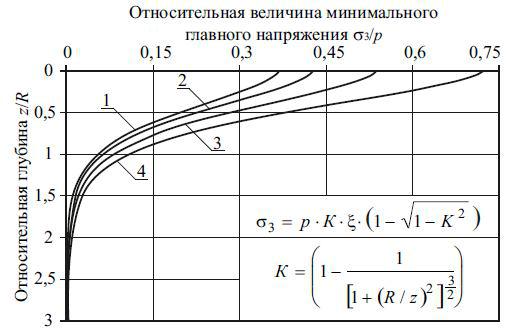
пространства работает в условиях трехосного с возможностью расширения в направлении минимальных главных напряжений. Изменение минимального главного напряжения по глубине приведено на рис. 2.3.

Рис. 2.3. Зависимость относительной величины минимального главного напряжения 3/р от относительной глубины z/R и коэффициента Пуассона при расчете по формуле (2.26): 1–4 – при величине коэффициента Пуассона =0,27, =0,30, =0,35, =0,42 соответственно

Из анализа результатов расчета, представленных на рис. 2.3 и формулы (2.5), следует, что чем меньше коэффициент Пуассона, тем больше значения коэффициента бокового давления и минимального главного напряжения. Это приводит к уменьшению девиатора напряжений при увеличении коэффициента Пуассона. Отсюда следует, что в песках ( =0,27) девиатор напряжения выше, по сравнению с аналогичной характеристикой напряженного состояния в глине ( =0,42), при воздействии на эти грунты одинаковой нагрузки.

Используя формулы табл. 2.2, можно рассчитать различные характеристики напряженного состояния. На рис. 2.4 и 2.5 приведены зависимости касательных и нормальных напряжений, возникающих на площадках, повернутых к главным осям под углом 45 о, а также на октаэдрических площадках от относительной глубины и величины коэффициента Пуассона.

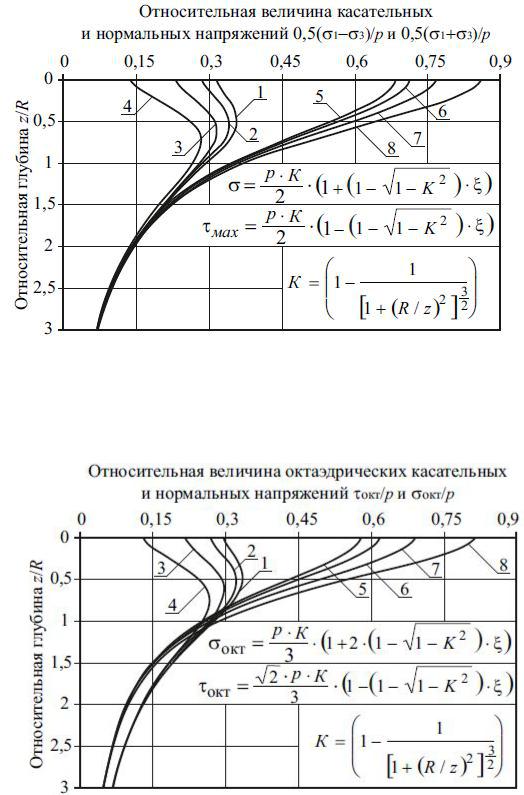
Рис. 2.4. Эпюры относительных напряжений, возникающих на площадках, повернутых к главным площадкам под углом 45о: 1–4 – максимальные касательные напряжения при коэффициенте Пуассона 0,27; 0,3; 0,35 и 0,42; 5–8 – нормальные напряжения при коэффициенте Пуассона 0,27; 0,3; 0,35 и 0,42

Рис. 2.5. Эпюры относительных напряжений на октаэдрических площадках при расчете по модифицированной модели А. Лява: 1–4 – октаэдрические касательные напряжения при коэффициенте Пуассона 0,27; 0,3; 0,35 и 0,42; 5–8 –октаэдрические нормальные напряжения при коэффициенте Пуассона 0,27; 0,3; 0,35 и 0,42

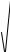
Из анализа данных, представленных на рис. 2.4, следует, что при увеличении коэффициента Пуассона максимальное касательное напряжение уменьшается, а величина нормального напряжения, действующего на этой площадке, возрастает. По глубине величина максимальных касательных напряжений изменяется, но в отличие от нормальных напряжений, экстремальное значение находится не на поверхности полупространства, а на некотором расстоянии от нее. Таким образом, наиболее опасная точка для третьей теории прочности расположена на некоторой глубине от поверхности полупространства. Если в этой точке максимальное касательное напряжение достигнет величины, равной сопротивлению недренированному сдвигу, то в данной точке возникнет предельное состояние по третьей теории прочности. Аналогичная картина имеет место при расчете других характеристик напряженного состояния, например, наибольшее октаэдрическое касательное напряжение тоже возникает на некоторой глубине от поверхности. Из анализа данных рис. 2.4 и 2.5 следует, что глубина расположения точки с экстремальными касательными напряжениями зависит от коэффициента Пуассона. Такая зависимость сохраняется в любом условии пластичности. В двухпараметрических условиях пластичности на местоположение наиболее опасной точки оказывает влияние один из параметров материала, ответственный за гашение касательного напряжения. Так в критерии Кулона – Мора таким параметром является угол внутреннего трения грунта. Для каждого из условий пластичности расстояние от поверхности полупространства до наиболее опасной точки индивидуально. Ордината точки с экстремальным касательным напряжением зависит от модели расчета главных напряжений. Это можно показать, выполняя модификацию модели М.И. Якунина, согласно которой в сечении по оси симметрии нагрузки максимальное главное напряжение определяется по формуле

1 а

сл

(2.28)

Еосн

1 а

где hэ – эквивалентная толщина слоя, заменяющего двухслойную систему, м; а – коэффициент концентрации, принимаемый равным 1 (для нежестких дорожных одежд) или 2,5 (для упругих изотропных тел); с – показатель степени радикала, обычно принимаемый равным 2,5 или 3; Есл и Еосн – соответственно модуль упругости материала слоя и модуль упругости подстилающего основания, МПа.

Представив формулу (2.28) в виде произведения давления и коэффициента затухания максимального главного напряжения по глубине, получим

1 р К ;

1 а

сл

(2.29)

Еосн

Подставив зависимость (2.29) в выражение (2.23), получим

3 р 1 а Dz c

сл

1 а

Еосн

Е	2	2
	2

сл			.(2.30)
			.(2.30)
Еосн

Полученная нами формула (2.29) позволяет модифицировать общепринятую модель М.И. Якунина так, что появляется возможность рассчитывать минимальные главные напряжения на любой глубине слоя или полупространства (Есл/Еосн=1). Зависимость (2.30), так же, как и предыдущая модифицированная модель А. Лява, в сечении по оси симметрии нагрузки на поверхности полупространства приводит к компрессионному сжатию грунта, а на бесконечности к одноосному сжатию. Причем величина минимальных главных напряжений в точках на поверхности оси симметрии нагрузки z=0 и на бесконечности z= одинакова по обеим модифицированным моделям, а во всех остальных точках их значения различны. Это обусловлено отличием результатов, получаемых по формулам (2.24) и (2.29), предназначенным для расчета коэффициентов затухания максимального главного напряжения.

Модифицированная модель М.И. Якунина позволяет вычислять характеристики напряженного состояния как в полупространстве (Есл/Еосн=1), так и слое конечной толщины 0 z hсл. Это обстоятельство дает возможность рассчитывать напряжения в песчаных дополнительных слоях оснований дорожных одежд, а также в слоях их оснований из дискретных материалов. На рис. 2.6 приведены эпюры изменения минимального главного напряжения по глубине полупространства (рис. 2.6, а) и слоя конечной толщины при Есл/Еосн=5 (рис. 2.6, б) при различных коэффициентах Пуассона. Из анализа данных рис. 2.6, а и 2.6, б следует, что на величину главного напряжения 3 оказывает влияние как коэффициент Пуассона, так и отношение мо-

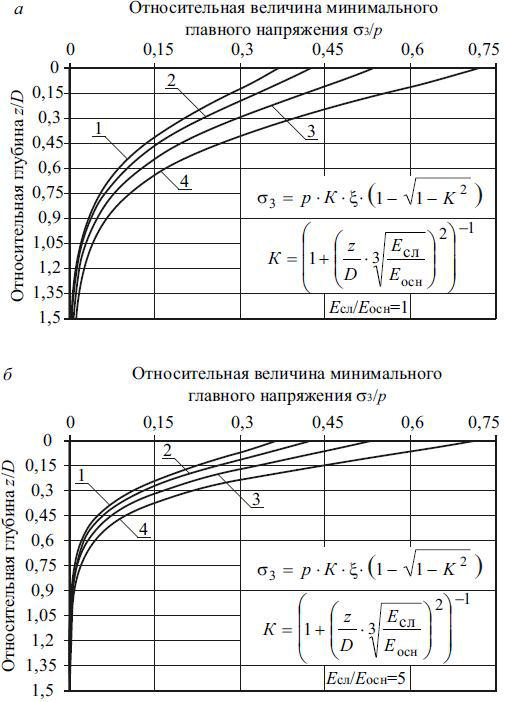
дулей упругости материала слоя, в котором вычисляются напряжения, и подстилающего этот слой полупространства.

Рис. 2.6. Зависимость относительной величины минимального главного напряжения 3/р от относительной глубины z/D и коэффициента Пуассона при расчете по формуле (2.30): а – для полупространства при Есл/Еосн=1; б – для слоя конечной толщины при Есл/Еосн=5; 1–4 – при величине коэффициента Пуассона =0,27, =0,30, =0,35, =0,42 соответственно

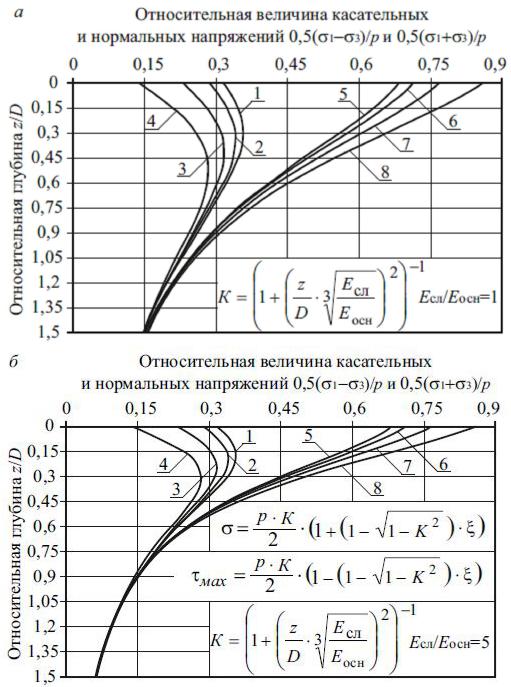
На рис. 2.7 и 2.8 приведены эпюры напряжений на площадках, повернутых к главным осям под углом 45о, и на октаэдрических площадках, вычисленные по модифицированной модели М.И. Якунина.

Рис. 2.7. Зависимость относительной величины касательных и нормальных напряжений на площадках, повернутых к главным осям под углом 45о, от относительной глубины и коэффициента Пуассона по модифицирован-

ной модели М.И.	Якунина: а – при	Есл/Еосн=1; б – при Есл/Еосн=5;
1–4 – касательные	напряжения при ,	равном 0,27; 0,3; 0,35 и 0,42;

5–8 – нормальные напряжения при , равном 0,27; 0,3; 0,35 и 0,42

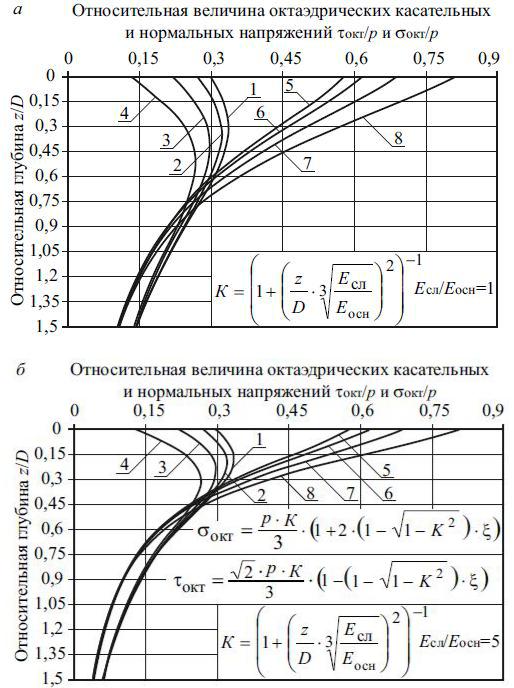
Рис. 2.8. Зависимость относительной величины октаэдрических касательных и нормальных напряжений от относительной глубины и коэффициента Пуассона при расчете по модифицированной моде-

ли М.И. Якунина: а – для полупространства при Есл/Еосн=1; б – для слоя конечной толщины при Есл/Еосн=5; 1–4 – относительная величина октаэдрических касательных напряжений при коэффициенте Пуассона 0,27; 0,3; 0,35 и 0,42; 5–8 – относительная величина октаэдрических нормальных напряжений при коэффициен-

те Пуассона 0,27; 0,3; 0,35 и 0,42

При применении этой модифицированной модели наблюдается аналогичная качественная зависимость характеристик напряженного состояния от коэффициента Пуассона. Кроме того, появляется возможность рассчитывать характеристики напряженного состояния в слое конечной толщины, ограничивая ординату z толщиной слоя. В этом случае величина любой характеристики напряжённого состояния зависит как от относительной глубины точки и коэффициента Пуассона материала слоя, так и отношения модулей материала слоя и общего модуля упругости подстилающего полупространства.

Отметим, что применение метода Н. Одемарка [106] позволяет модифицировать модель А. Лява так, что она станет подобной модели М.И. Якунина. Применяя метод Н. Одемарка, получим зависимость, в соответствии с которой приведенная по жесткости ордината точки в массиве грунта к ординате точки в слое дорожной одежды определяется по формуле

z zсл 3	Есл	,	(2.31)

	Еосн

где zсл – ордината точки, расположенной в сечении по оси симметрии нагрузки в пределах рассматриваемого слоя толщиной h, то есть 0 zсл h, м.

С учетом (2.31) формулу А. Лява, предназначенную для расчета максимального главного напряжения, представим в виде

										2	3
											2
					R			Е	осн		2
					R			Е
	р К ;	К 1					3					.	(2.32)
							3
			1	z				Е
1				z		сл		Е
						сл			сл

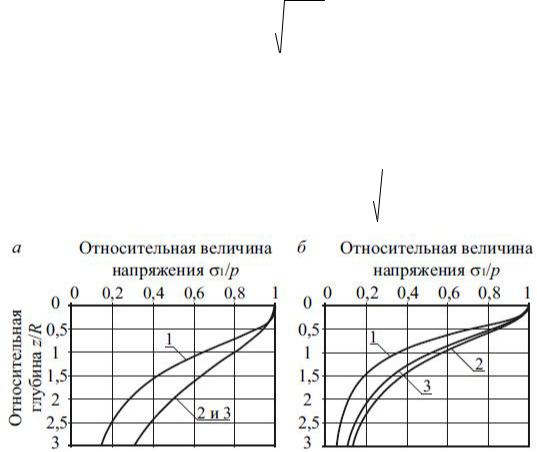
Рис. 2.9. Эпюры относительных максимальных главных напряжений:

а – полупространство при Есл/Еосн=1 и Еосн/ Есл =1; б – слой конечной

толщины при Есл/Еосн=5 и Еосн/ Есл =0,2; 1 – по формуле (2.32); 2 и 3 – по формуле М.И. Якунина (2.28) при коэффициенте с=2,5 и с=3

На рис. 2.9 представлены результаты расчета главного напряжения, выполненного по формулам (2.28) и (2.32).

Подставив зависимость (2.31) в формулу А. Лява, предназначенную для расчета 2 и 3 (см. табл. 1.1), получим

															2	1
																2
																2
		1 2μ									R			Еосн
		1 2μ									R			Еосн
2	3	р											3
2	3	р		р 1 μ 1									3
		2								zсл				Есл

										2		3
			р			R						2
			р			R		Е				2
							3		осн			.				(2.33)
							3
				1	z			Е
		2			z			Е
						сл			сл

В формулах (2.32) и (2.33) применена комбинация идей А. Лява и Н. Одемарка, вследствие чего эти зависимости условно назовем оригинальной моделью Лява – Одемарка. При Еосн/Есл=1 результаты расчета по формулам (2.31) и (2.32) совпадают с величинами напряжений, вычисленных по формулам А. Лява. В этом случае недостатки модели А. Лява сохраняются в (2.33).

Применив предлагаемый способ расчета минимального главного напряжения, заключающийся в подстановке (2.32) в (2.23), получим

													3
												2	2
					R				Е			2	2
					R				Е	осн
							3			осн
							3
3 р 1 1									Есл
				zсл					Есл



											2	3
					R			Е			2	3
					R			Е
	1	1	1			3			осн					.	(2.34)
	1	1	1			3								.	(2.34)
				z				Е
					сл				сл

Формула (2.34) позволяет вычислить минимальные главные напряжения, возникающие в слое конечной толщины. Так как эта зависимость получена по предлагаемому нами способу (2.23), то (2.32) и (2.34) назовем модифицированной моделью Лява – Одемарка. Подробно способ Н. Одемарка рассмотрен в первой части монографии3. При этом отметим, что метод Н. Одемарка основан на приравнивании изгибных жесткостей двух слоев, вследствие чего получается уравнение, решением которого является формула для расчета эквивалентной

3 Александров А.С. Совершенствование расчета дорожных конструкций по сопротивлению сдвигу в грунте земляного полотна. Ч. 1. Состояние вопроса. – Омск : СибАДИ. – 2015. – 292 с.

толщины, аналогичная зависимости (2.31). Рассматриваемые нами слои дорожной одежды из дискретных материалов не могут работать на изгиб. В этом заключается основной недостаток способа Н. Одемарка. В формуле М.И. Якунина этот недостаток компенсируется тем, что в формулу для расчета максимального главного напряжения введены поправочные коэффициенты а и с, позволяющие учесть отличия в величинах напряжений, возникающих в жестких и нежестких дорожных одеждах. Поэтому модифицированная модель М.И. Якунина (2.29) и (2.30) по сравнению с оригинальной (2.32) и (2.33) модифицированной (2.32) и (2.34) моделью Лява – Одемарка более приближена к условиям трехосного сжатия, возникающего в щебеночных, гравийных и песчаных основаниях нежестких дорожных одежд.

Минимальные главные напряжения, вычисляемые по модифицированной модели Лява – Одемарка, приведены на рис. 2.10.

Рис. 2.10. Зависимость относительной величины минимального главного напряжения 3/р от относительной глубины z/R и коэффициента Пуассона при расчете по формуле (2.34) при Еосн/Есл=0,2: 1–4 – относительная величина максимальных касательных напряженийприкоэффициентеПуассона0,27;0,3;0,35 и0,42соответственно

Сопоставляя результаты расчета минимальных главных напряжений, представленные на рис. 2.6, б и 2.10, несложно убедиться в том, что для одинаковых условий модифицированная модель Лява – Одемарка на глубинах до z=0,7 R дает более высокие значения минимальных главных напряжений по сравнению с формулой (2.30).

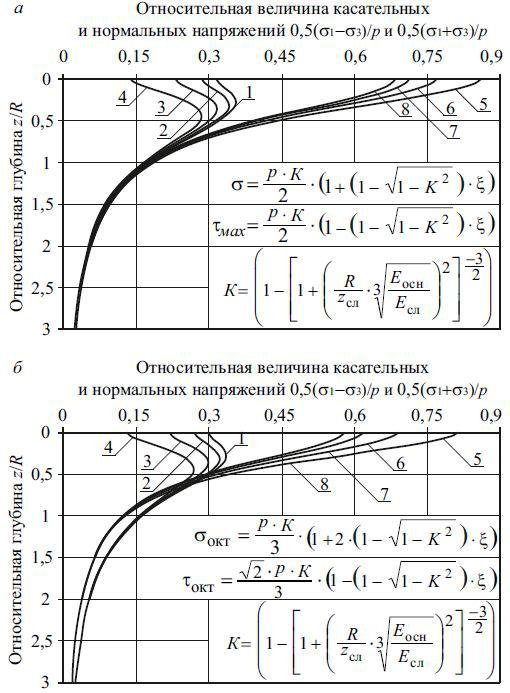
На рис. 2.11 приведены касательные и нормальные напряжения на различных площадках.

Рис. 2.11. Эпюры относительных касательных и нормальных напряжений при расчете по модифицированной модели Лява – Одемарка: а – напряжения, возникающие на площадках, повернутых к главным осям под углом 45о; б – октаэдрические напряжения; 1–4 –касательные напряжения при , равном 0,27; 0,3; 0,35 и 0,42 соответственно; 5–8 –нормальные напряжения при , равном 0,27; 0,3; 0,35 и 0,42

С.Р. Гонзалес для расчета нормальных вертикальных напряжений предложил в соответствующую зависимость А. Лява ввести параметр Фрелиха n, вследствие чего максимальные главные напряжения в сечении по оси симметрии нагрузки можно определять по формуле

[84, c. 3]:

			n
		R 2

1 р 1	1		.	(2.35)

		z

Сравнивая (2.35) с оригинальной формулой А. Лява (см. табл. 1.1), несложно заметить, что при n=3 эти зависимости тождественны. Выполнив подобное преобразование в формуле А. Лява, предназначенной для расчета минимальных главных напряжений, получим




		1 2 μ		1 μ					1
3	р	1 2 μ		1 μ					1				.	(2.36)
3	р	2					n			R	2	n	.	(2.36)
						2
					R	2	3
			1					2 1
			1					2 1
				z						z
				z

С.Р. Гонзалес параметр Фрелиха связывает с калифорнийским числом несущей способности грунта CBR, а расчет рекомендует выполнять по эмпирической формуле [84, c. 3]:

CBR 0,337

n 2 . (2.37)

Формулы (2.35) – (2.37) позволяют вычислять главные напряжения в различных грунтах в зависимости от параметра CBR. Условно эти формулы назовем оригинальной моделью Лява – Фрелиха – Гонзалеза. Очевидно, что при n=1,5 зависимость (2.36) тождественна формуле А. Лява, сохраняя ее недостатки, связанные с невозможностью учета структуры грунта при расчете максимального главного напряжения. Модифицируя эту модель, формулу (2.35) представим в виде

				n
			2
1 р К ;	К 1		R	.	(2.38)
		1

			z

Рис. 2.12. Эпюры относительных максимальных главных напряжений: 1–4 – при параметре Фрелиха n, равном 1; 1,5; 3 и 5 соответственно

Рис. 2.13. Эпюры относительных минимальных главных напряжений: 1–4 – при n=1 и , равном

0,27; 0,3; 0,35 и 0,42; 5–8 – при n=5 и , равном 0,27; 0,3; 0,35 и 0,42

Тогда подстановкой (2.38) в (2.23) получим

				n					n	2
			2	n				2	n
			R		1			R			. (2.39)
3	р 1	1				1 1	1
3	р 1	1				1 1	1
			z					z

Из анализа формул (2.35) и (2.38) следует, что увеличение параметра Фрелиха приводит к возрастанию максимального главного напряжения.

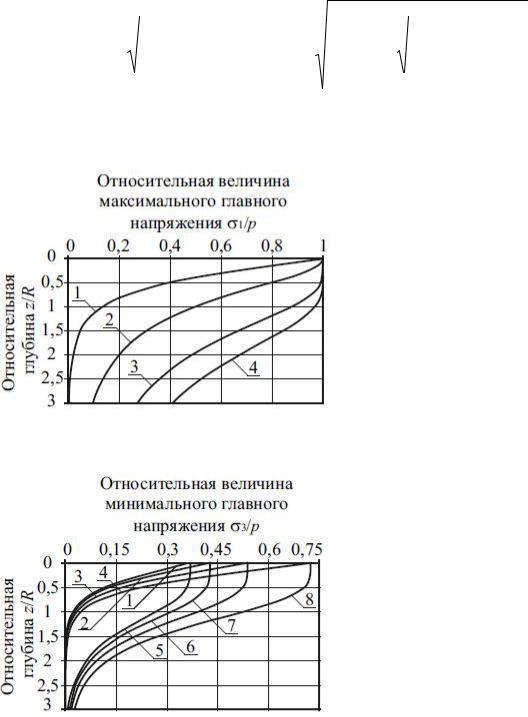
Зависимость относительных значений максимальных главных напряжений от относительной глубины и параметра Фрелиха приведена на рис. 2.12. На рис. 2.13

приведена зависимость минимальных главных напряжений модифицированной модели Лява – Фрелиха – Гонзалеса от глубины, параметра Фрелиха и коэффициента Пуассона. Данные рис. 2.12 и анализ формулы (2.37) позволяют сделать вывод, согласно которому в модели Лява – Фрелиха – Гонзалеса имеет место рост главных напряжений при увеличении калифорнийского числа несущей способности. Причем при n=5 и CBR=91 % в верхней области полупространства уменьшения максимального глав-

ного напряжения практически не происходит. В этом смысле модель Лява – Фрелиха – Гонзалеза подобна решениям механики зернистой среды.

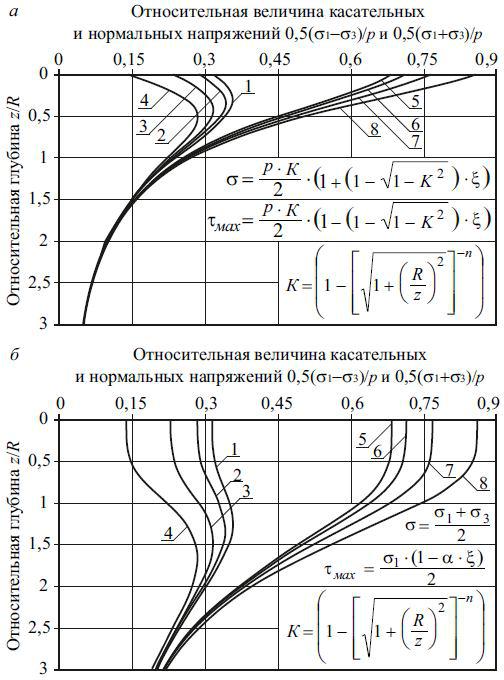
Минимальное главное напряжение, вычисленное по формуле (2.39), увеличивается при возрастании параметра Фрелиха n и коэффициента Пуассона . На рис. 2.14 приведены напряжения на площадке, повернутой к главным осям под углом 45о.

Рис. 2.14. Эпюры относительных касательных и нормальных напряжений на площадке, повернутой к главным осям под углом 45о, при расчете по модифицированной модели Лява – Фрелиха – Гонзалеса: а – при величине параметра Фрелиха n=1; б – при величине параметра Фрелиха n=5; 1–4 –касательные напряжения при , равном 0,27; 0,3; 0,35 и 0,42; 5–8 –нормальные напряжения при , равном 0,27; 0,3; 0,35 и 0,42

Из анализа данных рис. 2.14 следует, что увеличение параметра Фрелиха приводит к кардинальному изменению характера распределения максимальных касательных напряжений по глубине полупространства. Поэтому эта модель нуждается в тщательной экспериментальной проверке, которая должна касаться как количественного, так и качественного сравнения данных расчета и опытов.

Попытка ввода параметра Фрелиха в функции изменения по глубине нормального вертикального напряжения предпринята Р. Олсоном [110]. В сечении по оси симметрии нагрузки максимальные главные определяются по формуле [110]:

			z n		z 2	n

	р					2	.	(2.40)
1 z		1		1
1 z		1		1
			R		R

Отметим, что результаты расчетов по формулам (2.40) и (2.35) совпадают в том случае, если параметр n в выражениях (2.40) и (2.35) принимается одинаковым. Вследствие того, что экспериментальные данные [41] показывают, что параметр Фрелиха варьируется от 3 до 6, формула (2.37) должна иметь граничные условия по величине CBR. Анализируя формулу (2.40), отметим, что эта зависимость дает тождественные результаты с зависимостью А. Лява, если параметр Фрелиха в (2.40) равен 3.

Модифицируя модель Лява – Фрелиха – Олсона, формулу (2.40) представим в виде

		z n		z 2	n
1 р К ;		z n		z 2	2
	К 1		1		.	(2.41)
	К 1		1		.	(2.41)
		R		R

Подставив (2.41) в (2.23), получим

				z n					2			n
							z
							z					2
2 3 р 1					1
2 3 р 1				R	1			R
				R				R



									n	2
			z n						n
						z
						z	2		2
	1	1 1		1							.		(2.42)
	1	1 1		1							.		(2.42)
			R			R

Таким образом, модифицированная модель Лява – Фрелиха – Олсона (2.41) и (2.42) позволяет рассчитывать главные напряжения в грунтах при вариации параметра Фрелиха в традиционных пределах от n=3 до n=6.

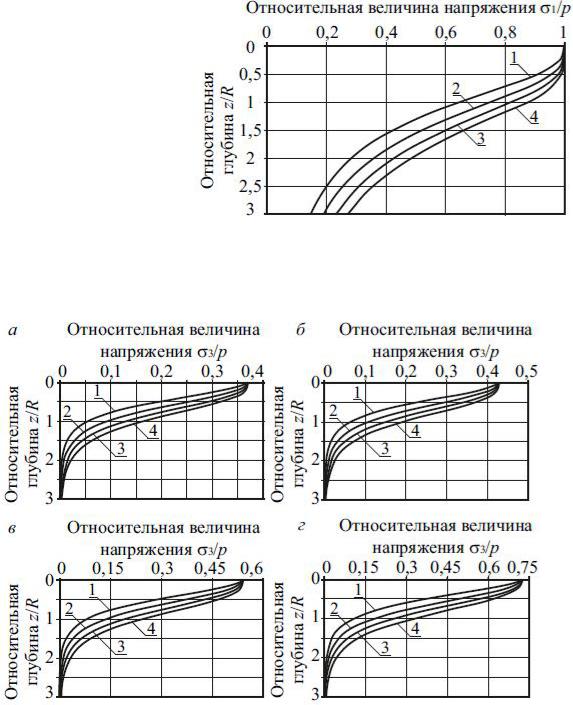
На рис. 2.15 приведена зависимость максимального главного напряжения по формуле Р. Олсона (2.40) или (2.41) от глубины и параметра Фрелиха. На рис. 2.16 представлены аналогичные зависимости для минимального напряжения и предлагаемой зависимости

(2.42).

Рис. 2.15. Эпюра относительных максимальных главных напряжений по формуле Р. Олсона (2.40): 1–4 – при параметре Фрелиха 3; 4; 5 и 6

Рис. 2.16. Эпюра относительных минимальных главных напряжений по формуле (2.42): а – при =0,27; б – при =0,3; в – при =0,35; г – при

=0,42; 1–4 – при параметре Фрелиха 3; 4; 5 и 6

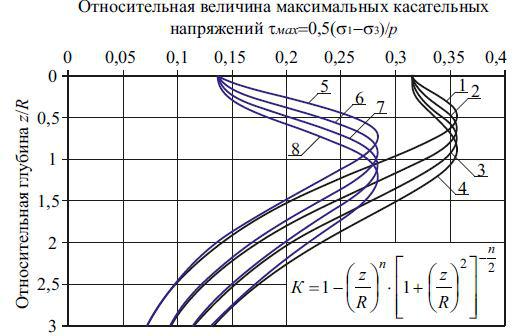
Из анализа данных рис. 2.15 и 2.16 следует, что при увеличении параметра Фрелиха величина главных напряжений возрастает. Следуя работе О.К. Фрелиха [80], для грунтов ненарушенного сложения принимают n=3, а для грунтов нарушенного сложения n=6. Если считать, что у грунтов нарушенного сложения жестких контактов между частицами меньше, то увеличение главных напряжений при возрастании параметра Фрелиха можно объяснить уменьшением числа жестких структурных связей между агрегатами и частицами грунта, что обуславливает ухудшение способности грунта рассеивать напряжение. Таким образом, оригинальная и модифицированная модель Лява – Фрелиха – Олсона имеет иной физический смысл по сравнению с оригинальной и модифицированной моделью Лява – Фрелиха – Гонзалеса.

Зависимость относительной величины максимальных касательных напряжений, рассчитанных по модифицированной модели Лява – Фрелиха – Олсона, от глубины, коэффициента Пуассона и параметра Фрелиха, приведена на рис. 2.17.

Рис. 2.17. Эпюра максимальных касательных напряжений по модифицированной модели Лява – Фрелиха – Олсона: 1 – 4 – при =0,27 и n 3; 4; 5 и 6 соответственно; 5 – 8 – при =0,42 и n 3; 4; 5 и 6 соответственно

Из анализа данных рис. 2.17 следует, что параметр Фрелиха оказывает неоднозначное влияние на величину максимальных касатель-

ных напряжений. В верхней части полупространства увеличение параметра Фрелиха приводит к более интенсивному затуханию касательного напряжения. Вследствие этого увеличение параметра Фрелиха приводит к снижению касательных напряжений, но только в верхней зоне полупространства. Примечательно то, что экстремальная величина касательных напряжений практически одинакова при изменении параметра n, а глубина расположения наиболее опасной точки увеличивается с ростом параметра Фрелиха. В нижней части полупространства при увеличении параметра Фрелиха касательное напряжение возрастает.

Модифицированные нами модели основываются на оригинальных моделях, которые в свою очередь являлись попыткой модификации формулы Лява, предназначенной для расчета вертикального нормального напряжения в сечении по оси симметрии нагрузки. Таким образом, в этих моделях применены различные инженерные способы решения задач для модификации одной из основных формул механики сплошной среды. Предлагаемый способ определения минимального главного напряжения (2.5), представленный в виде (2.23), позволяет модифицировать решения, полученные различными методами.

В механике зернистой среды получено два решения, позволяющие рассчитывать вертикальные нормальные напряжения по оси симметрии нагрузки, распределенной по круглой площадке. Такими решениями являются формулы И.И. Кандаурова [26, 27] и М. Хара [86, 87]. Записывая эти зависимости для определения максимальных главных напряжений в сечении по оси симметрии нагрузки, получим:

– по И.И. Кандаурову

		4	р	R2
	р 1 exp		р		,	(2.43)
	р 1 exp				,	(2.43)
1		z2

где р – коэффициент по пропорциональности, характеризующий распределительную способность среды (формулировка дана по И.И. Кандаурову [26, с. 8]. Впоследствии этот коэффициент стали называть коэффициентом распределительной способности среды);

– по Мильтону Хару

		R		2
	р 1 exp	R				.	(2.44)
	р 1 exp					.	(2.44)
1		2	р		z2
			р

При любом значении коэффициента р результаты расчета напряжений по формулам (2.43) и (2.44) не совпадают с результатами,

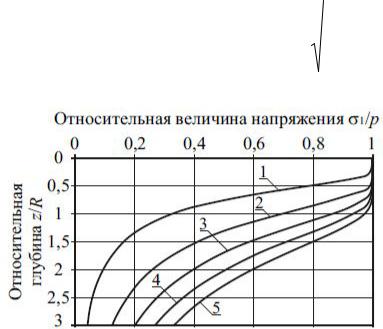
вычисленными по формуле А. Лява. В формуле И.И. Кандаурова уменьшение величины р приводит к уменьшению величины напряжения, а в зависимости М. Хара, наоборот, понижение параметра р обуславливает увеличение напряжений.

Модифицируя модель И.И. Кандаурова, формулу (2.43) представим в виде произведения давления и коэффициента затухания напряжения по глубине, то есть

4 р

1 р К ;

К 1 exp

(2.45)

Подставив (2.45) в обобщающую зависимость (2.23), получим

4 р R2

3 р 1 exp

1 1 exp

.(2.46)

На рис. 2.18 при-

ведены

относительные

значения максимально-

го

главного

напряже-

ния, вычисленные

по

формулам И.И. Кан-

даурова (2.43)

или

ее

аналогу (2.45) при раз-

личных коэффициентах

Рис. 2.18. Эпюра

относительных

максимальных

Пуассона.

Из

анализа

данных

рис.

2.18 сле-

главных напряжений, вычисленных по формуле

дует, что при увеличе-

(2.43) или (2.45): 1 – 5 – при р, равном 0,1; 0,3;

0,5; 0,7 и 0,9

нии параметра Фрелиха

величина

1/р

возрас-

тает. Другим отличием от результатов расчета по традиционной формуле А. Лява является менее интенсивное уменьшение максимального главного напряжения в верхней части полупространства. Вследствие этой особенности модель И.И. Кандаурова способна описывать формирование клина из переуплотненного грунта под равномерно распределенной нагрузкой. То есть результаты расчета напряжений по формуле (2.43) или аналогичному ей выражению (2.45) качественно соответствуют рассеиванию напряжений, представленному на рис. 2.18. На рис. 2.19 приведены зависимости минимальных главных на-

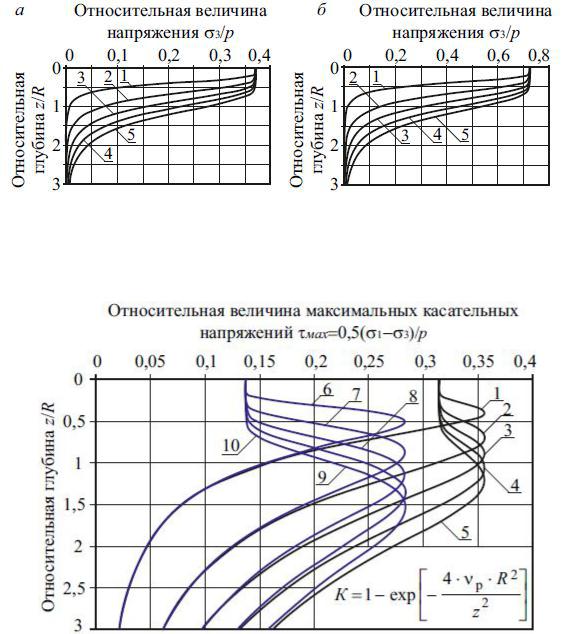
пряжений от глубины и параметра р, рассчитанные по модифицированной модели И.И Кандаурова, то есть по предлагаемой формуле (2.46). При увеличении коэффициента Пуассона и параметра р величина минимальных главных напряжений возрастает.

Рис. 2.19. Эпюра относительных минимальных главных напряжений, вычисленных по формуле (2.46): а – при коэффициенте Пуассона =0,27; б – при коэффициенте Пуассона =0,42; 1 – 5 – при р, равном 0,1; 0,3; 0,5; 0,7 и 0,9

Рис. 2.20. Эпюра максимальных касательных напряжений по модифицированной модели И.И. Кандаурова: 1 – 5 – при =0,27 и р,

равном 0,1; 0,3; 0,5; 0,7 и 0,9; 6 – 10 – при =0,42 и р, равном 0,1; 0,3; 0,5; 0,7 и 0,9

На рис. 2.20 приведены относительные значения максимальных касательных напряжений, рассчитанные с применением формул (2.45)

и (2.46). Из анализа данных рис. 2.20 следует, что при расчете напряжений по модифицированной модели И.И. Кандаурова в верхней части грунтового полупространства возникает достаточно мощная зона компрессионного сжатия, что не может иметь места от нагрузки, передаваемой конструктивными слоями дорожной одежды. Аналогичный недостаток имеет модифицированная модель М. Хара, по которой главные напряжения определяются по формулам

										R2
			р К ;					К 1 exp						.					(2.47)
			р К ;					К 1 exp						.					(2.47)
		1								2	р	z2
										2	р	z2


						2										2		2
				R		2							R			2
3	р 1 exp			R				1	1 1 exp				R						. (2.48)
3	р 1 exp			2			z2	1	1 1 exp			2					z2		. (2.48)
				2	р		z2					2			р		z2
					р										р

М.П. Болштянский выполнил серию экспериментов, определив величину параметра р, и модифицировал формулу И.И. Кандаурова, приведя зависимость (2.43) к виду [6]:

1	р		.	(2.49)
1		z 2	.	(2.49)
		z 2
	1 2,25
	1 2,25
		D

Представим (2.49) в виде

							z 2 1
	1	р К ;			К 1 2,25			.		(2.50)
	1	р К ;			К 1 2,25			.		(2.50)
							D

Тогда, подставив (2.50) в (2.23), получим
				1
			z 2	1				z 2	2
			z 2					z 2		. (2.51)
3	р 1 2,25				1	1 1 2,25
3	р 1 2,25				1	1 1 2,25
			D					D

Зависимость главных напряжений, вычисленных по формулам (2.50) и (2.51) от глубины и коэффициента Пуассона, приведена на рис. 2.21.

Из анализа данных, приведенных на рис. 2.21, следует, что оригинальное решение М.П. Болштянского (2.49) или его аналог (2.50) дает результаты, близкие к решению А. Лява (табл. гл. 1). Следовательно, результаты расчета максимального главного напряжения по формулам М.П. Болштянского будут близки к значениям этих напряжений, вычисляемых по формулам А. Лява.

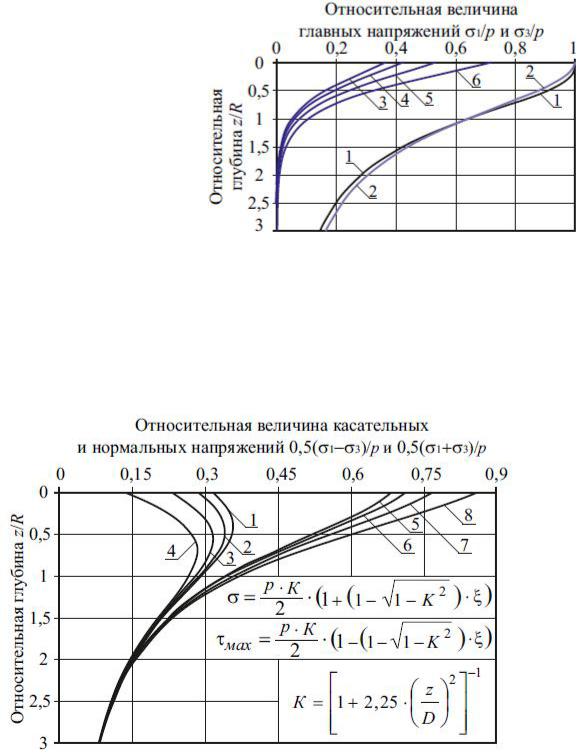
Вследствие близости результатов расчета максимальных главных напряжений, минимальные главные напряжения, вычисляемые по модифицированным моделям А. Лява (2.26) и М.П. Болштянского, (2.51) тоже будут иметь

достаточно близкие	ре-	Рис. 2.21. Эпюра относительных главных напря-
зультаты.		жений, вычисленных по модифицированной мо-
На рис. 2.22 приве-		дели М.П. Болштянского: 1 и 2 – максимальные
дена зависимость	на-	главные напряжения по формулам М.П. Бол-
пряжений, возникающих		штянского и А. Лява; 3 – 6 – минимальные глав-
пряжений, возникающих		ные напряжения по формуле (2.51) при 0,27;
на площадке, поверну-		ные напряжения по формуле (2.51) при 0,27;
на площадке, поверну-		0,3; 0,35 и 0,42 соответственно
той к главным осям под

углом 45о, от глубины и коэффициента Пуассона.

Рис. 2.22. Эпюры максимальных касательных и нормальных напряжений, возникающих на площадках, повернутых к главным осям под углом 45о, от относительной глубины и коэффициента Пуассона при расчете по модифицированной модели М.П. Болштянского: 1 – 4 – максимальные касательные напряжения при коэффициенте Пуассона 0,27; 0,3; 0,35 и 0,42 соответственно; 5 – 8 – нормальные напряжения на площадке с максимальным касательным напряжением при коэффициенте Пуассона 0,27; 0,3; 0,35

и 0,42

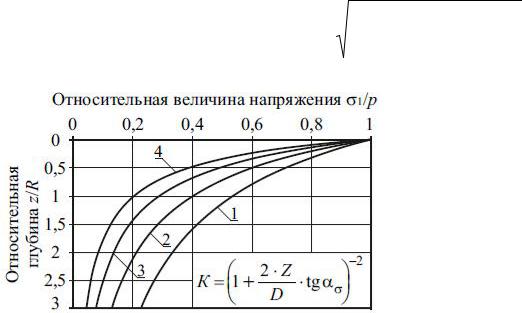
Большую группу методов расчета нормальных вертикальных напряжений в сечении по оси симметрии нагрузки составляют инженерные способы, к которым можно отнести оригинальную и модифицированные модели распределяющей способности. В соответствии с оригинальной моделью предполагается, что распределение нагрузки в полупространстве происходит под некоторым углом, называемым углом рассеивания напряжения . Б.С. Радовский сообщает, что эта модель предложена Е. Головачевым, а вычисление напряжения производится по формуле [50]:

		2 z		2
z	р 1		tg	.	(2.52)
z	р 1	D	tg	.	(2.52)
		D

В соответствии с (2.52) в сечении по оси симметрии нагрузки величину максимального главного напряжения можно определить по формулам

		2 z		2
1 р К ;	К 1		tg	.	(2.53)
1 р К ;	К 1	D	tg	.	(2.53)
		D

Применив предлагаемый способ расчета минимального главного напряжения в сечении по оси симметрии нагрузки (2.23), получим

			2 z		2			2 z
						1
2	3	р 1		tg			1 1
			D					D

tg	4	. (2.54)
tg		. (2.54)


	На рис. 2.23 приве-
	дена зависимость отно-
	сительных		максималь-
	ных главных напряже-
	ний,	возникающих по
	оси симметрии нагруз-
	ки от величины			угла
	рассеивания		напряже-
	ний.	При	увеличении
Рис. 2.23. Эпюра относительных максимальных	угла	рассеивания		на-
	пряжения уменьшают-
главных напряжений по оси симметрии нагрузки,
	ся. В	формуле (2.54)
вычисленных по (2.52) и (2.53): 1 – 4 – при ,
равном 20; 30; 40 и 50 о соответственно	имеет	место аналогич-

ная зависимость между минимальными главными напряжениями и углом рассеивания напряжения. Величина минимальных напряжений на поверхности полупро-

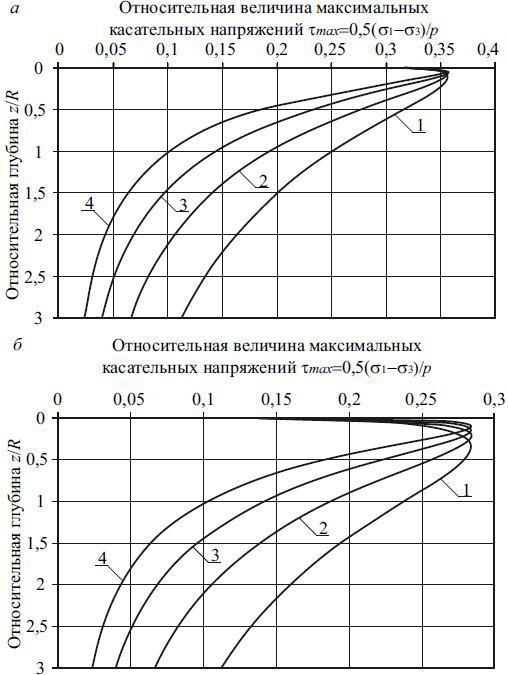
странства, вычисляемых по формуле (2.54), так же, как и во всех предыдущих модифицированных моделях, соответствует компрессионному сжатию. На рис. 2.24 приведена зависимость относительных максимальных касательных напряжений от глубины и угла рассеивания напряжений.

Рис. 2.24. Эпюра относительных максимальных главных напряже-

ний: а – при =0,27; б – при =0,42; 1 – 4 – при , равном 20; 30 ; 40 и 50 0 соответственно

В настоящее время нет экспериментальных методик, позволяющих вычислить угол рассеивания напряжений непосредственно из результатов опытов по распределяющей способности грунтов. Поэтому этот параметр связывают с характеристиками грунта, определяемыми по результатам других опытов. Например, в работах [74, 82, 83, 103] угол рассеивания напряжения связывается с сопротивлением недренированному сдвигу, которое определяется по данным неконсолидированных недренированных испытаний грунтов трехосным сжатием в стабилометре. Е. Головачев считал, что угол рассеивания напряжения численно равен углу естественного откоса от, определяемого по данным сравнительно простых опытов. Подстановка в формулу (2.52) угла естественного откоса приводит к зависимости

			2 z	2
z	р		2 z		(2.55)
			D
		1	D	tg от .
			0

Представив формулу (2.55) в виде произведения давления и коэффициента затухания с последующей подстановкой этого коэффициента в (2.23), получим

			2 z	2
1 р К ;	К		2 z		(2.56)
			D
		1	D	tg от .
			0

			2
		2 z
2 3 р		2 z
				1
	1	D0	tg от	1
		D0

2 z

11 D0

4

	. (2.57)
tg от	. (2.57)

Известно, что угол естественного откоса связывают с углом внутреннего трения . В общем виде эту взаимосвязь можно представить некоторой функцией

		от	f .				(2.58)
Подставив зависимость (2.58) в выражения (2.56) и (2.57), полу-
чим						2
					2 z	2
		р К ;	К		2 z		(2.59)
		р К ;	К	1			(2.59)
	1				D
				0

				2
			2 z
	р		2 z
	р	1			1
3			D0
			D0

1 1

2D0z tg f . (2.60)

Г.К. Клейн сообщает [28, с. 35], что испытания песка средней крупности, выполненные П.А. Миняевым, показали, что при угле ес-

тественного откоса от=32о угол внутреннего трения составляет=39,67о. Кроме того, Г.К. Клейн [28, с. 35] приводит результаты опытов с рыхлыми песчаными и гравелистыми грунтами, выполненные Н.В. Немиловым, согласно которым углы естественного откоса и внутреннего трения составляют от=33о и =46о. Отсюда следует, что угол внутреннего трения для песчаных грунтов может быть представлен долей от угла естественного откоса, а следовательно, и долей угла рассеивания напряжения, то есть

от	;	,	(2.61)

где – коэффициент пропорциональности, характеризующий отношения угла естественного откоса к углу внутреннего трения или отношение угла рассеивания напряжения к углу внутреннего трения.

Из формулы (2.61) следует

			2 z
1 р К ;	К		2 z
			D
		1	D
			0

		(2.62)
tg	2
		(2.63)
	.	(2.63)

		2 z		2
		2 z	tg
	р 1				1
	р 1				1
3		D0
		D0

2 z

11 D0

tg . (2.64)

К.С. Теренецкий приводит формулу португальских специалистов, в соответствии с которой угол рассеивания напряжений определяется по формуле [55, с. 37]:

30 25 lg	Eд сл	,	(2.65)
	Eд о

где Ед(сл) и Ед(о) – модули деформации дискретного материала слоя и грунта, подстилающего слой, Па.

Эта зависимость позволяет модифицировать (2.52) –(2.54), применить зависимости к расчету главных напряжений к слою конечной толщины. Кроме формулы (2.65) для модификации моделей распределяющей способности для их применения к расчету напряжений в слое конечной толщины может быть применен способ Н. Одемарка. В моделях распределяющей способности может быть учтен эффект усталости материала слоя или грунта полупространства, связанный с изменениями структуры. Это можно сделать двумя способами. Пер-

вый способ реализуется введением в модель формулы Дж. Ленга [103], в соответствии с которой в процессе приложения нагрузки угол рассеивания напряжения уменьшается. Формула Ленга имеет вид

[103, с. 73]:

tan N	1	,	(2.66)
tan 1	k lgN

где 1 и N – углы рассеивания напряжения при реализации 1-го по счету приложения нагрузки и N-го количества приложенных нагрузок; N – общее суммарное число нагрузок.

Из зависимости (2.66) следует

tan N	tan 1	.	(2.67)

	k lg N

Подстановка функции (2.67) в формулы (2.53) и (2.54) позволяет привести их к виду

2 z

tan

1 р К ;

К 1

k lg N

2 z

tan

2 3 р 1

k lg N

2 z

tan

k lgN

Подставив в эти зависимости (2.63) и (2.64), получим

		2 z		tan		2
р К ;	К 1		tg			,

1		D			k lgN

(2.68)

(2.69)

(2.70)

где 1 – угол внутреннего трения при реализации 1-го по счету приложения нагрузки, град или рад.

						2 z			tan		2
2 3 р						2 z
								tg
				1				tg
							D		k lg N

					2 z			tan			4
					2 z
	1	1					tg					.	(2.71)
	1	1	1				tg		k lg	N		.	(2.71)
					D				k lg	N

Второй способ состоит в подстановке в зависимости (2.63) и (2.64) значений углов внутреннего трения, регламентируемых ОДН

218.046-01 и соответствующих суммарному числу реализованных расчетных нагрузок. В этом случае получим

2 z

1 р К ;

2 z

р 1

2 z

1 1

2
	.	(2.72)
	.	(2.72)

(2.73)

Внормативном документе [46] функциональная зависимость угла внутреннего трения от относительной влажности и суммарного числа приложенных расчетных нагрузок задана таблично.

Внастоящее время известно достаточно большое количество формул, связывающих угол рассеивания напряжений с различными параметрами грунта, что позволяет выполнить модификацию основной модели Е. Головачева. Применяя предлагаемый нами способ (2.23), эти модели можно модифицировать так, что появится возможность рассчитывать минимальное главное напряжение, а значит и все другие характеристики напряженного состояния.

К инженерным методам расчета напряжений относится зависимость, предложенная А.В. Смирновым, позволяющая выполнять расчет нормального вертикального напряжения во времени, то есть учитывать эффекты удара. В соответствии с этой зависимостью вертикальное нормальное напряжение вычисляют по формуле

4 N

sin

(2.74)

где l – длина фронта распространения напряжений, м; 0 – коэффициент, характеризующий затухание напряжений в среде, м-1; С0 – скорость распространения продольных волн, м/с.

Модифицируя зависимость (2.74), получим

р К sin

;

К l 0 C0 t .

(2.75)

l 0 C0 t 1

р sin

1 l 2 0 C0 t

(2.76)

Полученные нами модифицированные модели содержат коэффициент бокового давления, который при компрессионном сжатии является функцией коэффициента Пуассона, то есть

	.	(2.77)

1

Для песчаных и гравелистых грунтов коэффициент Пуассона принимают =0,27. Такое значение коэффициента Пуассона может иметь место при давлениях, варьирующихся в определенном диапазоне, в котором связь напряжений и деформаций линейна. При более высоких давлениях коэффициент Пуассона является функцией глав-

ных напряжений. В табл. 2.2 приведены формулы для определения переменного коэффициента поперечной деформации (коэффициента Пуассона).

Таблица 2.2. Зависимости для расчета переменного коэффициента

Пуассона

Автор

Формула

2 G

С.С. Вялов [9]

где K( ) и G( ) – переменные модули объемной деформа-

ции и сдвига, которые могут быть определены по функцио-

нальным зависимостям K( ) и G( ) от главных напряжений

или компонент тензора

1 у 1 2 у

;

и о

; и о

2 1 у 1 2 у

;

и о

И.А. Биргер [4]

где у – коэффициент Пуассона при работе материала в упругой стадии, являющийся постоянной материала; – функция пластичности; и(о) и и(о) – относительные интенсивности напряжений и деформаций

0,5 0,2 n	и о ,
Н.А. Махутов [35]
где 1/п – показатель нелинейности

Р.Дж. Хикс и К.Л.

2 A

Монисмит [90]

где А0, А1, А2

и А3 – параметры материала

;

М. Карасахин [99]

p ср2 ср1;

pm 0,5 ср1 ср2 ; qm 0,5 q1

q2 ,

где ср1 и ср2 – средние нормальные напряжения от двух

смежных степеней напряженного состояния, ср2> ср1; q1 и

q2 – девиаторы напряжений от

двух смежных степеней на-

пряженного состояния, q2> q1

При возникновении напряжений, величина которых приводит к=0,5, возникает гидростатическое сжатие, характеризуемое 1= 2= 3 и 1=0, 2=0, 3=0. В соответствии с фундаментальной зависимостью (2.77) величина коэффициента бокового давления составляет =1. В этом случае классические формулы (2.3) дают равенства 1= 2 и1= 3. Такие же равенства получаются по предлагаемым нами формулам (2.5) и (2.23), но только в точке, расположенной на поверхности в сечении по оси симметрии нагрузки, в которой =1 и К=1. Гидростатическое сжатие в этой верхней точке можно получить, рассчитывая коэффициент бокового давления по моделям механики сыпучей среды, к которой относят песчаные и гравелистые грунты, а также гранулированные материалы. В настоящее время известен ряд формул, позволяющих вычислять коэффициент бокового давления в зависимости от величины угла внутреннего трения. Основные функциональные зависимости коэффициента бокового давления от угла внутреннего трения приводятся и анализируются в работах Г.К. Клейна [28], А.Л. Строковой [54], а также в первой части этой монографии. Для анализа зависимости коэффициента бокового давления от угла внутреннего трения рассмотрим зависимости Ж. Биареза, Дж. Жаки и Е. Брукера.

Г.К. Клей сообщает, что зависимость Ж. Биареза описывает зависимость коэффициентов бокового давления от угла внутреннего трения при испытании грунта в гибкой резиновой обойме, а зависимость Дж. Жаки – при компрессионных испытаниях [28, с. 37]. Следуя Г.К. Клейну, формула Ж Биареза имеет вид [28, с. 37]:

	1	sin	.	(2.78)

1		sin

Формула Дж. Жаки [97] и тождественная ей зависимость Жаки – Михайловского [105, с. 1431]:

	2		1		sin
1		sin				.	(2.79)
	3			1
					sin

Формулы (2.78) и (2.79) предназначены для расчетов коэффициентов бокового давления при испытаниях материалов по двум диаметрально противоположным схемам, то есть в абсолютно гибкой и жесткой обойме. Если =0 или =90, то обе модели дают одинаковые результаты =1 и =0, что соответствует значениям, вычисляемым по

(2.77) при =0,5 и =0. То есть (2.78) и (2.79) в случае =0 описыва-

ют текучий материал, а при =90 – абсолютно хрупкий. Если 0< <90, то результаты вычислений по зависимостям (2.78) и (2.79) разнятся.

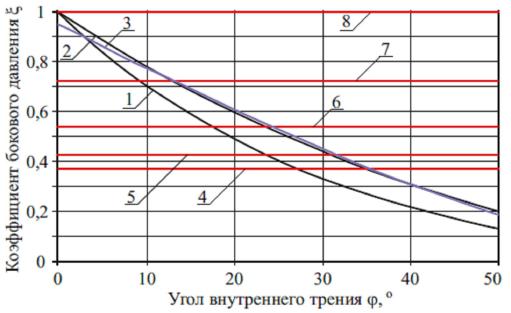
Результаты расчетов по моделям других авторов при вариации угла внутреннего трения в диапазоне 0< <90, как правило, находятся в интервале значений , вычисляемых по формулам (2.78) и (2.79). Исключения составляют модели типа Брукера – Ирланда [71], постулирующие невозможность равенства коэффициента бокового давления 1 при =0. Формула Брукера – Ирланда [71] имеет вид

0,95 sin . (2.80)

На рис. 2.25 приведены результаты расчета коэффициента бокового давления по формулам (2.77) – (2.80).

Рис. 2.25. Зависимость коэффициента бокового давления от угла внутреннего трения и коэффициента Пуассона: 1 – 3 – при расчете по формулам (2.78); (2.79) и (2.80) соответственно; 5 – 8 – при расчете по формуле (2.77) при величине коэффициента Пуассона 0,27; 0,3; 0,35; 0,42 и 0,5 соответственно

Из анализа данных рис. 2.25 следует, что прямые, описываемые уравнением (2.77), и кривые, построенные по формулам (2.78) – (2.80), имеют по одной точке пересечения. Вследствие этого при вычислении минимальных главных напряжений по формулам (2.5) или (2.23) с расчетом коэффициента бокового давления по зависимости (2.77) или (2.78) – (2.80) могут совпадать лишь в сравнительно малом диапазоне варьирования угла внутреннего трения. Решив уравнение (2.77) относительно коэффициента Пуассона и подставив вместо коэффициента бокового давления его функциональную зависимость от угла внутреннего трения (2.78), получим

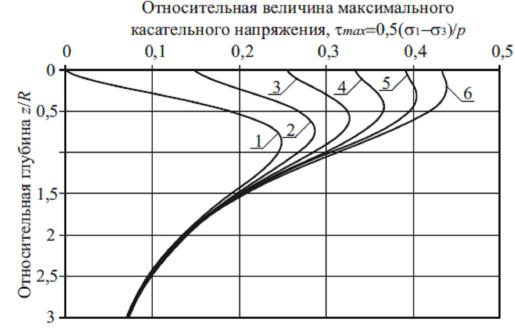
	1 sin		1 sin 1
		1		.	(2.81)
	1 sin
1			1 sin

Формула (2.81) позволяет рассчитывать значения коэффициента Пуассона в зависимости от угла внутреннего трения. Из анализа формулы (2.81) следует, что при увеличении угла внутреннего трения коэффициент Пуассона уменьшается, значит, величина коэффициента бокового давления, вычисляемая по выражению (2.77), тоже становится меньше. Отсюда делаем вывод, что увеличение угла внутреннего трения приводит к увеличению минимальных главных напряжений, а следовательно, всех девиаторных характеристик напряженного состояния (максимального касательного напряжения, октаэдрического касательного напряжения, интенсивности касательного напряжения и т.п.). На рис. 2.26 приведена зависимость максимальных касательных напряжений от глубины и угла внутреннего трения.

Рис. 2.26. Эпюра относительных значений максимальных касательных напряжений, вычисленных с применением формулы (2.78) или (2.81): 1 – 6 – при угле внутреннего трения 0; 10; 20; 30; 40 и 50 о

Анализируя данные рис. 2.26, необходимо отметить, что результаты расчета касательных напряжений противоречат результатам расчета по другим условиям пластичности. Например, в оригинальном критерии Кулона – Мора касательные напряжения C–M вычисляются по формуле

C M	1		1 3	tg	1 3	.	(2.82)
	cos
		2		2

Из (2.82) следует, что тригонометрические функции угла внутреннего трения приводят к увеличению уменьшаемого и вычитаемого. Уменьшаемым в (2.82) является максимальное касательное напряжение, которое делится на косинус угла внутреннего трения, вследствие чего данная составляющая уравнения (2.82) возрастает при увеличении . Это качественно соответствует данным рис. 2.26, но в зависимости (2.82) имеется вычитаемое, представляющее собой нормальное напряжение, то есть направленное перпендикулярно площадке, вдоль которой действует максимальное касательное напряжение, которое умножается на тангенс угла внутреннего трения, вследствие чего величина вычитаемого тоже возрастает при увеличении угла внутреннего трения от 0 при =0 до ( 1- 3)/2 при =45 и продолжает возрастать при >45. Кроме того, максимальное касательное напряжение определяется половиной разности главных напряжений, а нормальная составляющая – половиной суммы этих характеристик. Поэтому максимальное главное напряжение меньше нормального к этой площадке напряжения на величину 3. Вследствие этих особенностей касательное напряжение по критерию Кулона – Мора уменьшается при увеличении угла внутреннего трения, принимая экстремальное значение при =0, а уравнение (2.82) вырождается в третью теорию прочности для грунтов. Отсюда следует, что вычисленные нами максимальные касательные напряжения, представленные на рис. 2.26, должны являться составляющей условия пластичности, например критерия Кулона – Мора. В качестве третьей теории прочности могут быть использованы значения, рассчитанные только при =0, но эти значения будут тождественны величинам, вычисленным с привлечением формулы (2.77) при =0,5.

Таким образом, предложенный модифицированный способ расчета минимальных главных напряжений может реализовываться двумя путями, в соответствии с которыми (2.23) представим в виде

						1				.
	2 3 р K							1 K2				(2.83)
					1
							1				.
			1	sin
2	3	р K							1 K2			(2.84)

		1		sin

В первом случае, описываемом формулой (2.83), предполагается, что =cons’t, величина которой соответствует данным справочной ли-

тературы. В уравнении (2.84) значение коэффициента бокового давления зависит от угла внутреннего трения. Возможность применения формул (2.83) и (2.84) необходимо установить сравнением с данными экспериментов.

Песчаные грунты обладают еще одним существенным отличием от связных грунтов, заключающемся в принципиально ином распределении контактных давлений по поверхности полупространства. Штамповые испытания песчаных грунтов показывают, что эпюра контактных давлений имеет параболическую форму [76, 110]. Эта особенность песчаных грунтов нашла свое отражение в работах, направленных на вывод формул для расчета нормальных вертикальных напряжений в сечении по оси симметрии круглого штампа.

В работе [101] для расчета нормальных вертикальных напряжений в песчаном полупространстве получена формула

		2	2 a3
z	2 р 1 2 a				,	(2.85)

				2
			1 a	2
			1 a

где а – отношение z/R.

Представив формулу (2.85) в виде произведения давления и коэффициента затухания максимального главного напряжения для сечения, расположенного по оси симметрии нагрузки, получим

			2	2 a3
1	р К ;	К 2 1 2 a				.	(2.86)

					2
				1 a	2
				1 a

Подстановка зависимости (2.86) в уравнение (2.23) позволяет получить формулу

2 3 2 р 1 2 a2 21 aa32

			2 a3	2
		2	2 a3
1	1 4 1 2 a				.	(2.87)


			1 a2
			1 a2

Р. Олсон нашел решение, в соответствии с которым расчет нормальных вертикальных напряжений в сечении по оси симметрии нагрузки при параболическом распределении давления по поверхности песчаного полупространства выполняется по формуле, включающей параметр О.К. Фрелиха,

		2 a	2	2 a	n	1 a2	2 n
z	2 р 1						n	.	(2.88)

		2 n		2 n

Применив предлагаемый способ, получим

2 a

1 a2

2 n

р К ;

К 2 1

(2.89)

2 n

2 a

1 a2

2 n

2 р 1

2 n

2 a2

2 an

1 4

1 a

(2.90)

2 n

Таким образом, этот способ позволяет выполнить модификацию любой модели, предназначенной для расчета нормального вертикального напряжения в сечении по оси симметрии нагрузки. Суть способа состоит в том, что в сечении по оси симметрии нагрузки направления главных осей совпадают с декартовой системой координат, что вследствие равенства 1= z позволяет вычислять максимальные главные напряжения по оригинальным формулам, предложенным другими авторами. Минимальное главное напряжение представлено в виде произведения максимального главного напряжения, коэффициента бокового давления и нового коэффициента , являющегося непрерывной функцией глубины. В результате появляется возможность расчета минимальных главных напряжений и всех характеристик напряженного состояния в формулах, полученных методами механики зернистой среды и инженерными способами расчета. Ранее такой возможности не имелось. Решение А. Лява, полученное при помощи методов механики сплошной среды, а именно аппарата дифференциально интегрального исчисления, модифицировано путем замены оригинальной формулы для расчета минимального главного напряжения зависимостью, полученной по предлагаемому способу. В результате на поверхности земляного полотна грунт испытывает компрессионное сжатие, а во всех остальных точках рассматриваемого сечения значения минимального главного напряжения положительны. Таким образом, во всех точках сечения за исключением поверхности полупространства возможность грунта испытывать деформации бокового расширения обусловлена тем, что удерживающие напряжения меньше

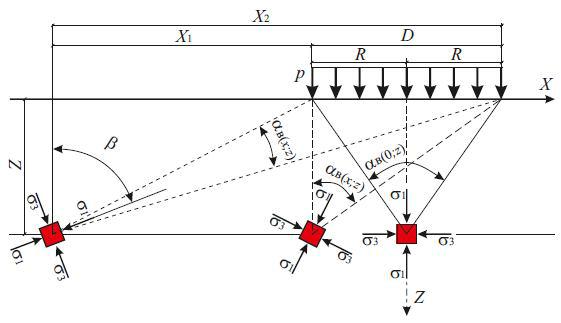
величины, необходимой для компрессии. В оригинальном решении А. Лява эти напряжения на некоторой глубине принимали отрицательные значения, то есть становились растягивающими.

Предпримем попытку расчета главных напряжений и компонент тензора в точках, расположенных вне оси симметрии нагрузки. При этом отметим, что применяемый способ расчета минимального главного напряжения не позволяет задействовать математический аппарат механики сплошной среды. Для расчета напряжений вне оси симметрии нагрузки можно применить коэффициенты затухания главных напряжений в горизонтальном направлении, значения которых вычисляются из решения механики сплошной среды. Рассматривая такие решения механики грунтов, отметим, что их можно разделить на два типа. В решениях первого типа, применяемых для расчета напряжений от нагрузки, распределенной по круглой площадке, направление максимальных главных напряжений задается вращением оси симметрии нагрузки. В этом случае минимальные главные напряжения могут принимать отрицательные значения в некотором множестве точек полупространства. Следовательно, решения этой группы применять нерационально. В решениях второй группы направление главных напряжений задается биссектрисой угла, получаемого вращением замкнутого контура. В этом случае минимальные главные напряжения имеют положительные значения во всех точках полупространства. На рис. 2.27 приведена расчетная схема Мичелла.

Рис. 2.27. Схема для определения ориентации главных напряжений в горизонтальной плоскости по мере удаления от оси нагрузки

В соответствии со схемой Мичелла направление максимального главного напряжения 1 совпадает с биссектрисой угла видимости в, а направление минимального главного напряжения перпендикулярно биссектрисе этого угла. В решении Мичелла главные напряжения и компоненты тензора определяются по формулам, представленным в табл. 2.3, а углы в(0; z) и в(x; z) вычисляются по формулам табл. 2.4.

Таблица 2.3. Формулы Мичелла, применяемые для расчета

характеристик напряженного состояния от нагрузки, распределенной по полосе

Напряжение

Формула

Максимальное главное напряжение

sin

Минимальное главное напряжение

sin

Нормальное вертикальное напряжение

sin

cos2

Нормальное горизонтальное напряжение

sin

cos2

Касательное напряжение =

sin

Таблица 2.4. Формулы для определения углов в схеме Мичелла

Местоположение

Формула

точки

По оси симметрии нагрузки

в 0;z 2 arctg

2 arctg

2 Z

в x;z arctg

arctg

;

X1 A D;

Под нагруженной площадкой

X2 1 A D

В сечении, проходящем через

в x;z

arctg

край нагрузки

За пределами нагруженной

в x;z

arctg

;

X1 A D;

площадки

X2 1 A D

Примечание. Х1 и Х2 – расстояние от точки до соответствующего края нагрузки; А – число, определяемое отношением Х1 к D.

Решения механики сплошной среды позволяют определить вариацию величины напряжений и направлений главных площадок в

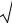
горизонтальной плоскости. В механике грунтов общепринятым считается решение Мичелла, предназначенное для расчета напряжений, возникающих от воздействия равномерно распределенной нагрузки по бесконечной полосе или в основании насыпи. Как приближение это решение может быть использовано при расчете напряжений в слоях дорожной конструкции из дискретных материалов, воспринимающих нагрузку, распределенную по полосе, вырезанной в одном из направлений круглой площадки. На рис. 2.4 приведена расчетная схема к решению этой задачи.

Суть приближения заключается во вводе в формулы табл. 2.4 относительных коэффициентов, являющихся функциями координат. Для напряжений 1 и 3 эти коэффициенты определяются по формулам

Kг1		в x;z sin в x;z	; Kг3		в x;z sin в x;z	,	(2.91)
	в 0;z sin в 0;z			в 0;z sin в 0;z

где в(0; z) и в(x; z) – углы на схеме Мичелла для глубины Z, на которой по формулам табл. 2.4 определены осевые напряжения, рад.

С учетом зависимостей (2.91) расчет главных напряжений в общем виде можно представить формулами

	р К		в x;z sin в x;z		.		(2.92)
	р К				.		(2.92)
1		в 0;z sin в 0;z
		в 0;z sin в 0;z
2 3 р K 1				в x;z sin в x;z		.
			1 K2	в x;z sin в x;z			(2.93)
			1 K2				(2.93)
				в 0;z sin в 0;z

Аналогичным образом можно получить зависимости для расчета компонент тензора напряжений. Отметим, что предлагаемый способ в случае непрерывности функции коэффициента затухания максимального главного напряжения К позволяет получить неразрывные функции (2.92) и (2.93). Это несложно продемонстрировать, опираясь на теоремы, регламентирующие операции над непрерывными функциями. Согласно этим теоремам сумма, произведение и разность двух непрерывных функций есть функция непрерывная. Частное двух непрерывных функций также является непрерывной функцией за исключением точки, в которой функция, находящаяся в знаменателе, принимает нулевое значение. Таким образом, если функция К непрерывна, то и функции (2.92) и (2.93) непрерывны, за исключением точек, в которой z= или x= . Таким образом, функции (2.91) и (2.93) имеют разрыв только на бесконечности, а этого вполне достаточно для практических расчетов грунта земляного полотна.

2.3. Сопоставление теоретических и экспериментальных данных

Специалистами дорожной отрасли поставлены эксперименты по определению напряжений, возникающих в слоях дорожной одежды и грунте земляного полотна. Такие эксперименты выполнены посредством испытаний моделей дорожных конструкций кратковременной, в том числе ударной, нагрузкой, а также при помощи испытаний подвижной нагрузкой. Испытания подвижной нагрузкой выполняются на кольцевых стендах и являются наиболее приближенными к условиям эксплуатации дорожных конструкций. Постановка таких экспериментов отличается большой трудоемкостью, требующей:

–устройства дорожной конструкции, включающей земляное полотно и дорожную одежду;

–размещения в слоях дорожной одежды измерительной аппара-

туры;

–монтажа оборудования, комплектующего имитатор нагрузки. Вследствие высокой трудоемкости и стоимости кольцевых стен-

дов полученные при их помощи экспериментальные данные представляют большую ценность. В диссертации Брюса Даниэля Стивена приведены данные испытаний дорожных конструкций, выполненных на кольцевом стенде, в ходе которых измерены вертикальные и горизонтальные деформации и нормальные напряжения по оси симметрии нагрузки и за ее пределами [116]. Испытания выполнены на кольцевом стенде университета Кентербери, расположенного в отдельном здании. Схема кольцевого стенда приведена на рис. 2.28.

Рис. 2.28. Схема кольцевого стенда университета Кентербери (г. Крайстчерч, южный остров Новой Зеландии)

Общий вид кольцевого стенда университета Кентербери приведен на рис. 2.29, а на рис. 2.30 представлен рабочий момент установки тензометров, применяемых для измерения вертикальной деформации.

Для измерения напряжений применены месдозы «Dynatest Soil Pressure Cell» [116, рис. 3.6].

Рис. 2.29. Кольцевой стенд университета Кентербери [539, с. 160]

Рис. 2.30. Размещение тензометров (Emu) на границе раздела земляного полотна и основания из щебеночно-песчаной смеси [116]

При обработке данных, снимаемых с датчиков давлений, напряжение (кПа), возникающее в точке измерений, определяется по формуле

	Vout	,	(2.94)

Vbridge A C

где Vout – измеренное напряжение, mV; Vbridge – напряжение, Vbridge=12 V; А – коэффициент, корректирующий размерность, А=1000; С – калибровочный пара-

метр, С=200 10-5 1/кПа.

Для измерения напряжений применены месдозы, измеряющие напряжения в двух разных диапазонах. Датчики низких давлений, измеряющие напряжения в диапазоне 20 – 200 кПа, установлены в земляном полотне. Датчики высоких давлений (80-800 кПа) закладывались в основание дорожной одежды.

Испытания выполнены в два этапа. На первом этапе кольцевой стенд был разбит на четыре сегмента, в пределах которых устроена одинаковая конструкция дорожной одежды, но с различным материалом щебеночного основания. На втором этапе построены две разные конструкции дорожной одежды, а стенд разбит на пять сегментов. В пределах каждого сегмента применялся определенный щебеночный материал. В табл. 2.5 приведены применяемые щебеночные материалы и толщина слоев основания из них.

Таблица 2.5. Щебеночные материалы и толщина слоев основания [116, с. 86]

Сегмент кольце-	Характеристика	Первый этап ис-	Второй этап ис-
вого стенда	конструкции	пытаний	пытаний
А	Материал	TNZ M4	AUS FCR
А	Толщина слоя, мм	275	275
	Толщина слоя, мм	275	275
В	Материал	TNZ M4	AUS FCR
В	Толщина слоя, мм	275	200
	Толщина слоя, мм	275	200
C	Материал	AUS FCR	TNZ M4
C	Толщина слоя, мм	275	200
	Толщина слоя, мм	275	200
	Материал	Ресайклированный	TNZ M4
D		материал
	Толщина слоя, мм	275	275
E	Материал	Конструкция не	TNZ M5
E	Толщина слоя, мм	построена	275
	Толщина слоя, мм	построена	275

Примечание. TNZ M4 и TNZ M5 – местные щебеночные материалы, соответствующие требованиям стандартов Новой Зеландии; AUS FCR – австралийский щебеночный материал, импортированный из г. Мельбурн и соответствующий требованиям стандартов Австралии.

Характеристики щебеночных материалов, применяемых для устройства оснований, приведены в табл. 2.6.

Таблица 2.6. Характеристики щебеночных материалов [116, с. 85]

Характеристика			TNZ	TNZ M4	TNZ	AUS	Ресайклирован-
Характеристика			M4	+ fines	M5	FCR	ный материал
			M4	+ fines	M5	FCR	ный материал
Размер	наиболее	крупной	40	40	40	20	40
фракции, мм			40	40	40	20	40
фракции, мм
Содержание частиц, про-
шедших	сквозь	сито 75	3	8	4	9	7
мкм, %
Максимальная стандартная			2,32	2,36	2,38	2,26	2,12
плотность, т/м3			2,32	2,36	2,38	2,26	2,12
Оптимальная влажность, %			6,0	4,8	4,2	6,0	10,5

На всем протяжении кольцевого стенда устроено асфальтобетонное покрытие толщиной 25 мм, что соответствует требованиям стандартов Новой Зеландии [116, c. 84]. В земляном полотне использован местный суглинок, характеристики которого приведены в табл. 2.7.

Таблица 2.7. Характеристики суглинка земляного полотна [116, с. 85]

Характеристика	Величина
Максимальная стандартная плотность, т/м3	1,87
Оптимальная влажность, %	14
Влажность на границе текучести, %	28
Влажность на границе раскатывания, %	14
Число пластичности, %	14
Содержание частиц, прошедших сквозь сито 75 мкм, %	72

Рис. 2.31. Отпечаток шин 11R22.5 при нагрузке на колесо 40 кН и давлении воздуха 750 кПа

Рис. 2.32. Отпечаток шин 11R22.5 при нагрузке на колесо 60 кН и давлении воздуха 750 кПа

Для определения площади контакта шин с покрытием дорожной одежды с них были сняты отпечатки. Б.Д. Стивен отмечает, что при увеличении нагрузки на колеса длина контакта шины с покрытием возрастает, а ширина пятна контакта остается прежней [116, c. 98]. Таким образом, увеличение нагрузки на колесо приводит к увеличению площади контакта за счет возрастания его длины. По мнению Б.Д. Стивена, пятно контакта необходимо моделировать двумя способами: в виде прямоугольника или круга. При расчете давлений нагрузка на шину принимается 20 или 30 кН [116]. В табл. 2.8 приведены размеры отпечатка шин и вычисленные контактные давления.

Таблица 2.8. Геометрические характеристики пятен контакта шин

11R22.5 при различных нагрузках на колесо

Характеристика	Величина при нагрузке на колесо
Характеристика	40, кН	50, кН	60, кН
	40, кН	50, кН	60, кН
Ширина пятна контакта одной шины, мм	225	225	225
Длина пятна контакта одной шины, мм	243	277	303
Расстояние между шинами, мм	125	125	125
Нагрузка на шину, кН	20	25	30
Давление от шины, кПа	366	401	440
Диаметр круга, равновеликого по площади	264	282	295
отпечатку одной шины, мм	264	282	295
отпечатку одной шины, мм
Ширина пятна контакта колеса, мм	450	450	450
Длина пятна контакта колеса, мм	243	277	303
Нагрузка на колесо, кН	40	50	60
Давление от колеса, кПа	366	401	440
Диаметр круга, равновеликого по площади	373	398	417
отпечатку колеса, мм	373	398	417
отпечатку колеса, мм

Примечание. Характеристики пятна контакта для колеса вычислены автором.

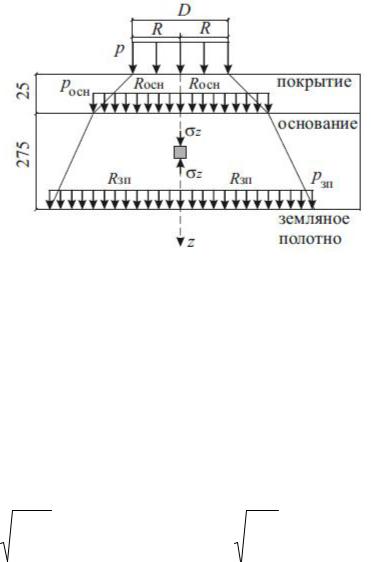
В табл. 2.9 приведены значения измеренных нормальных вертикальных напряжений в модели дорожной конструкции сегмента А на станции №7 [116, с. 101].

Таблица 2.9. Экспериментальные значения вертикальных нормальных

напряжений, измеренные на станции № 7 в сегменте кольцевого стенда А

Глубина, мм			Конструктивный слой			Материал слоя	Напряжение
Глубина, мм			Конструктивный слой			Материал слоя	z, кПа
							z, кПа
0			Покрытие			Асфальтобетон	366
75							319,4
150			Основание			Щебеночный материал	173,6
225			Основание			Щебеночный материал	98,0
225							98,0
300							37,8
375			Земляное полотно			Суглинок	36,7
Для			вычисления
нормальных			вертикаль-
ных напряжений в до-
рожной		конструкции
применена схема после-
довательного				расчета
напряжений			в	каждом
слое (рис. 2.33). В соот-
ветствии с этой схемой
нагрузка,	передаваемая
верхним слоем, пере-					Рис. 2.33. Схема для расчета нормальных верти-
распределяется				по по-	Рис. 2.33. Схема для расчета нормальных верти-
верхности	постилающе-				кальных напряжений по оси симметрии нагрузки

го полупространства. Диаметр площадки распределения давления возрастает от слоя к слою, а величина контактных давлений уменьшается. Для применения рассмотренных нами оригинальных формул для расчета нормальных вертикальных напряжений необходимо вычислить диаметры (радиусы) площадок на поверхности щебеночного основания и грунта земляного полотна. Контактные давления на поверхности щебеночного основания и земляного полотна измерены, вследствие чего известны. Диаметры круглой площадки, по которой распределены эти давления, вычислены по формулам

D	2 R	D	p	;	D	2 R	D	p	,	(2.95)

осн	осн		pосн		зп	зп		pзп

где росн и рзп – давления, воспринимаемые основанием и земляным полотном, Па.

Результаты расчета диаметров площадок распределения нагрузок и экспериментальные значения контактных давлений приведены в табл. 2.10.

Таблица 2.10.	Экспериментальные значения контактных давлений
и соответствующие им диаметры площадок распределения нагрузки
Конструктивный	Материал слоя	Толщи-	Контактное	Диаметр
слой	Материал слоя	на, см	давление, кПа	площадки, см
Покрытие	Асфальтобетон	2,5	366	37,3
Основание	Щебеночно-	27,5	329,6	39,3
Основание	песчаная смесь	27,5	329,6	39,3
	песчаная смесь
Земляное полотно	Суглинок	–	37,8	116,1

Из анализа данных табл. 2.9 следует, что эпюры вертикальных напряжений можно построить только в щебеночном слое основания, в котором измерение вертикального нормального напряжения выполнено в трех точках, а также еще в двух точках, лежащих на границе этого слоя. Для земляного полотна проверка величины вертикального нормального напряжения возможна только в одной точке, лежащей на глубине 7,5 см от грунтовой поверхности.

Для расчета напряжений в щебеночном слое необходимо пересчитать ординаты точек относительно поверхности основания и указать соответствующие глубине залегания этих точек экспериментальные значения вертикальных нормальных напряжений. Результаты пересчета приведены в табл. 2.11.

Таблица2.11. Ординатыточек и экспериментальныезначения напряжений

Ордината точки от поверхности		Измеренная величина
покрытия, см	основания, см	напряжения, кПа
2,5	0	329,6
7,5	5,0	319,4
15,0	12,5	173,6
22,5	20,0	98,0
30,0	27,5	37,8

Таким образом, известны все необходимые входные параметры для расчета вертикального нормального напряжения по глубине щебеночного слоя. Диаметр и радиус площадки, по которой распределено давление на поверхности основания, принят по данным табл. 2.10 (D=39,3 см, R=19,65 см).

В первую очередь выполним расчет вертикальных нормальных напряжений по формуле А. Лява, которая для полупространства дана выражением (2.24), а для слоя конечной толщины зависимостью (2.32). Обращаем внимание, что по оси симметрии нагрузки главные оси совпадают с координатными осями, вследствие чего в этом сечении 1= z. Поэтому формулы (2.24) и (2.32) в сечении по оси симметрии нагрузки определяют максимальное главное напряжение как вертикальное нормальное напряжение, которые в данном сечении равны друг другу. Оценка погрешности результатов расчета выполнялась относительно экспериментальных данных, а вычисление простой ошибки выполнено по формуле

100	экс выч	,	(2.96)

	экс

где экс и выч – экспериментальные и вычисленные значения напряжений в сечении по оси симметрии нагрузки, Па.

Результаты расчета и погрешность формул (2.24) и (2.32) приведены в табл. 2.12.

Таблица 2.12. Сопоставление результатов расчета напряжений по

формулам (2.24) и (2.32) с данными эксперимента Брюса Стивена

	Нормальное вертикальное напряжение по				Погрешность, % по фор-
Глу-	оси симметрии нагрузки, кПа				муле
бина,	измерен-	вычисленное по формуле				(2.32) при Ещ/Егр
см	измерен-		(2.32) при Ещ/Егр		(2.24)
	ное	(2.24)				1	7
	ное	(2.24)	1	7		1	7
			1	7
0	329,6	329,6	329,6	329,6	0	0	0
5,0	319,4	324,658	324,658	301,969	-1,65	-1,65	5,46
12,5	173,6	278,6358	278,6358	177,600	-60,55	-60,55	-2,30
20,0	98,0	209,970	209,970	97,609	-114,26	-114,26	0,40
27,5	37,8	152,07	152,07	58,6433	-302,3	-302,3	-55,14

Примечание. Ещ= Есл и Егр=Еосн.

Расчет нормальных вертикальных напряжений по формуле (2.32) выполнен для реального отношения модулей упругости Еш/Егр=7 (в расчете по формуле (2.32) используется обратно пропорциональная величина Егр/Еш=7-1), а также при соотношении Еш/Егр=1. Второй расчет выполнен, чтобы обратить внимание на совпадение результатов расчета по (2.24) и (2.32) при Егр/Еш=1. Из анализа данных табл. 2.12 следует, что за исключением нижней точки, лежащей на поверхности

земляного полотна, зависимость Лява–Одемарка (2.32) дает вполне удовлетворительные результаты. Отсюда следует, что формула для расчета максимальных главных напряжений или нормальных вертикальных напряжений, возникающих в сечении по оси симметрии нагрузки помимо функции глубины, должна включать параметры материала.

В табл. 2.13 приведены значения напряжений, вычисленных по формуле М.И. Якунина, которая для сечения на оси симметрии нагрузки тождественна зависимостям (2.28) или (2.29).

Таблица 2.13. Сопоставление результатов расчета напряжений по

формуле М.И. Якунина (2.29) с данными эксперимента

Глубина,	Напряжение по оси симметрии нагрузки, кПа		Погреш-
Глубина,	Измеренное	Вычисленное по формуле	Погреш-
см	Измеренное	(2.29) при Ещ/Егр=7	ность, %
		(2.29) при Ещ/Егр=7
0	329,6	329,6	0
5,0	319,4	306,10	4,16
12,5	173,6	222,72	-28,30
20,0	98,0	147,91	-50,92
27,5	37,8	99,20	-162,44

Примечание. При расчете по формуле М.И. Якунина принято а=1 и с=2,5;

Ещ= Есл и Егр=Еосн.

Из анализа данных табл. 2.13 следует, что удовлетворительные результаты формулы (2.28) и (2.29) дают только в одной точке, расположенной на глубине 5 см. По точности формула М.И. Якунина уступает зависимости (2.32), но является более приемлемой по сравнению с выражением (2.24).

Формула (2.35) при подстановке в нее зависимости (2.31) примет

вид

							n
					2
					2
				R		Еосн
	1 р 1	1		R		Еосн	.	(2.97)
z					3
z					3
			zсл			Есл

В табл. 2.14 приведены результаты расчета напряжений по формуле (2.97) и ее погрешность. Расчеты выполнены при трех различных комбинациях параметров материала. Первый расчет выполнен при Есл/Еосн=1 и n=3. В этом случае результаты расчета (2.97) совпадают с величиной напряжений, полученной по формуле А. Лява (2.24). В двух других случаях принято реальное соотношение модулей упругости Есл/Еосн=7, а параметры n различны. Во втором случае па-

раметр Фрелиха вычислен по формуле (2.37) при величине калифорнийского числа несущей способности щебня CBR=100 %. В этом случае n=5,16. При такой величине параметра Фрелиха адекватность результатов расчета напряжений по формуле (2.97) экспериментальных данных является неудовлетворительной. Поэтому в последнем случае предпринята попытка поиска значения параметра n, при котором зависимость (2.97) дает удовлетворительные результаты хотя бы для некоторых точек.

Таблица 2.14. Сопоставление результатов расчета напряжений по

формуле (2.97) с данными эксперимента

	Нормальное вертикальное напряжение					Погрешность, % по формуле
Глу-	по оси симметрии нагрузки, кПа					(2.97)
Глу-		вычисленное по формуле (2.97)					при
бина,		вычисленное по формуле (2.97)					при	при
бина,	изме-		при		при	при n=3	n=5,16	при
см	изме-	при n=3	при		при	при n=3	n=5,16	n=0,75
	ренное	Ещ/Егр=1	n=5,16		n=0,75	Ещ/Егр=1	Ещ/Егр=	Ещ/Егр=7
		Ещ/Егр=1	Ещ/Егр=7	Ещ/Егр=7			7	Ещ/Егр=7
0	329,6	329,6	329,6		329,6	0	0	0
5,0	319,4	324,658	325,95		252,53	-1,65	-3,12	20,945
12,5	173,6	278,6358	307,45		172,61	-60,55	-87,762	0,57
20,0	98,0	209,970	272,82		118,30	-114,26	-213,72	-20,715
27,5	37,8	152,07	329,55		82,86	-302,3	-621,74	-119,25

Примечание. Ещ= Есл и Егр=Еосн.

Из анализа данных табл. 2.14 следует, что зависимость (2.37), рекомендуемая С.Р. Гонзалесом для вычисления параметра Фрелиха через величину CBR, не пригодна для расчетов напряжений в слоях из щебеночных материалов. При n=0,75 и Ещ/Егр=7 для точек, расположенных внутри слоя, формула (2.97) дает удовлетворительные результаты, но по точности существенно уступает зависимости (2.32). Кроме того, близкие результаты можно получить по формуле Лява – Фрелиха – Олсона (2.40) или (2.41). Подставив зависимость (2.31) в выражение (2.40), получим формулу


			z		сл
	z	р 1			сл
		р 1
1				R
				R

		n					2		n

								2
	Есл			zсл		Есл		2
	Есл			zсл		Есл				. (2.98)
3					3
3			1	R	3
	Еосн			R		Еосн

Формула (2.98) является модифицированной зависимостью (2.40), выполненной при помощи применения метода Н. Одемарка. Поэтому (2.98) назовем формулой Лява – Фрелиха – Олсона – Одемарка. Ре-

зультаты расчета по формуле (2.98) приведены в табл. 2.15. Если в формуле (2.98) принять Есл/Еосн=1 и n=3, то результаты расчета совпадают с напряжениями, вычисляемыми по выражению (2.24). Результаты расчета по зависимостям (2.32) и (2.98) тождественны при любых одинаковых значениях Есл/Еосн и n=3. Преимущество формулы (2.40) по сравнению с формулой (2.32) состоит в том, что подобрав величину параметра Фрелиха, можно повысить точность расчета. В табл. 2.15 приведены вычисленные по формуле (2.98) напряжения при

Есл/Еосн=7 и n=2,25, а также при Есл/Еосн=7 и n=3.

Таблица 2.15. Сопоставление результатов расчета напряжений по

формуле (2.98) с данными эксперимента

	Напряжение по оси симметрии нагрузки,			Погрешность, %
Глубина,		кПа		Погрешность, %
		кПа
		вычисленное	по формуле	при	при
см		вычисленное	по формуле	при	при
см	измеренное	(2.98) при Ещ/Егр=7 и n		Ещ/Егр=7	Ещ/Егр=7
	измеренное	(2.98) при Ещ/Егр=7 и n		Ещ/Егр=7	Ещ/Егр=7
		n=3	n=2,25	и n=3	и n=2,25
0	329,6	329,6	329,6	0	0
5,0	319,4	301,97	278,25	5,46	12,88
12,5	173,6	177,60	145,15	-2,30	16,39
20,0	98,0	97,61	76,32	0,40	22,12
27,5	37,8	58,64	45,04	-55,14	-19,16

Примечание. Ещ= Есл и Егр=Еосн.

В табл. 2.15 продемонстрировано, что при n=3 и Есл/Еосн=7 результаты расчета по формулам (2.32) и (2.98) совпадают. Изменение параметра Фрелиха n=2,25 при реальном соотношении модулей Есл/Еосн=7 позволило получить результаты, удовлетворительно согласующиеся с экспериментальными данными во всех точках слоя. При этом в точках, расположенных внутри слоя основания, более точные результаты получаются при n=3, но при n=2,25 с удовлетворительной точностью рассчитывается величина напряжения на границе раздела основания и земляного полотна. Поэтому появляется возможность вычислять контактные давления на поверхности земляного полотна с приемлемой для инженерных расчетов точностью. Это обстоятельство приобретает важность при проектировании дорожной конструкции, так как величина давления на поверхности слоя или полупространства обуславливает точность расчета напряжений по всей глубине данного элемента. Во всех ранее выполненных расчетах определить контактное давление на поверхности земляного полотна (нижняя точка щебеночного основания) не удавалось.

В основе проанализированных формул лежат зависимости, полученные на основе совершенствования формулы А. Лява, то есть основного решения теории сплошной среды. Кроме этих формул для расчета вертикального нормального напряжения можно применить зависимости, полученные методами механики зернистой среды. Отличие формул механики сплошной и зернистой среды состоит в различных математических аппаратах, применяемых для вывода решений. В механике сплошной среды используется дифференциальноинтегральное исчисление линейной теории упругости и задействуются все уравнения (статические уравнения Навье, геометрические уравнения Коши и Сен-Венана, а также физические уравнения в виде обобщенного закона Гука), позволяющие получить общее решение в виде системы дифференциальных уравнений, как правило, смешанного метода. В методах механики зернистой среды задействуется аппарат математической статистики. Одним из первых решений механики зернистой среды являются формулы И.И. Кандаурова. Решение И.И. Кандаурова для нагрузки, распределенной по круглой площадке, имеет вид формулы (2.43), в которую входит параметр материала р.

В табл. 2.16 приведены результаты расчета по этой зависимости.

Таблица 2.16. Сопоставление результатов расчета напряжений по

формуле (2.43) с данными эксперимента

	Напряжение по оси симметрии нагрузки,			Погрешность, %
Глубина,		кПа		Погрешность, %
		кПа
		вычисленное	по формуле
см		вычисленное	по формуле
см	измеренное	(2.43) при		р =0,37	р =0,07
	измеренное	(2.43) при		р =0,37	р =0,07
		р =0,37	р =0,07
0	329,6	329,6	329,6	0	0
5,0	319,4	329,6	325,24	-3,19	-1,83
12,5	173,6	321,90	164,60	-85,42	5,18
20,0	98,0	253,61	78,06	-158,79	20,34
27,5	37,8	177,92	43,91	-370,68	-16,16

Из анализа данных табл. 2.16 следует, что при традиционных значениях коэффициента распределительной способности среды ( р=0,37–0,38) зависимость И.И. Кандаурова дает результаты, плохо согласующиеся с данными эксперимента Б.Д. Стивена. Однако если выполнить подбор величины этого параметра, то можно добиться удовлетворительной сходимости вычисленных и экспериментальных напряжений во всех точках слоя, в том числе на нижней поверхности.

Для расчета напряжений в слое конечной толщины рассмотрим возможность применения в формуле И.И. Кандаурова метода Н. Одемарка. Подстановка зависимости (2.31) в формулу (2.43) приводит к решению

1 exp 4

осн

(2.99)

сл

Если в формуле (2.99) отношение модулей упругости (деформации) Еосн/Есл=1 (в выполняемом расчете Еосн=Егр и Есл=Ещ), то формулы (2.99) и (2.43) приводят к одинаковым результатам. При уменьшении отношения Еосн/Есл (в выполняемом расчете Егр/Ещ) напряжение в рассматриваемой точке увеличивается. То есть, чем слабее грунт в основании, подстилающем слой из дискретного материала, тем выше возникающие в нем напряжения и хуже распределяющая способность. Результаты расчета по формуле (2.99) приведены в табл. 2.17.

Таблица 2.17. Сопоставление результатов расчета напряжений по

формуле (2.99) с данными эксперимента

	Напряжение по оси симметрии нагрузки,			Погрешность, %
Глубина,		кПа		Погрешность, %
		кПа
		вычисленное	по формуле	при	при
см		вычисленное	по формуле
см	измеренное	(2.99) при
	измеренное	(2.99) при		р =0,37	р =0,257
		р =0,37	р =0,257	р =0,37	р =0,257
		р =0,37	р =0,257
0	329,6	329,6	329,6	0	0
5,0	319,4	328,96	325,30	-2,99	-1,85
12,5	173,6	208,28	164,98	-19,98	4,97
20,0	98,0	106,54	78,29	-8,71	20,12
27,5	37,8	61,50	44,04	-62,69	-16,51

Из анализа данных табл. 2.16 и 2.17 следует, что при традиционном значении коэффициента распределительной способности р =0,37 введение в формулу (2.43) зависимости (2.31) приводит к существенному увеличению точности расчета. Тем не менее при р =0,37 для нижней точки щебеночного основания расхождение результатов расчета по формуле (2.99) и данных эксперимента велико. Подбор параметра р, заключающийся в уменьшении его величины до р =0,257, позволяет вычислить нормальные вертикальные напряжения с приемлемой точностью. Если преследовать цель расчета напряжений в щебеночном слое конечной толщины с приемлемой точностью при р =0,37, то (2.99) нужно дать в виде

1 exp 4

осн

(2.100)

сл

где b – корректировочный коэффициент.

Из анализа (2.100) следует, что величина коэффициента р должна составлять 0,37, а значения параметра b могут варьироваться. В этом случае р теряет свой смысл, а его функцию выполняет параметр b. Отсюда следует, что ввод параметра b в (2.99) излишен, целесообразнее считать, что р может варьироваться и зависеть от показателей физических свойств слоя и подстилающего основания, которые не учитываются отношением модулей упругости в (2.99). Таким образом, параметр р является не постоянной, а функцией показателей физических свойств и текстуры гранулированного материала (щебня, гравия, песка).

Зарубежным аналогом формулы И.И. Кандаурова является формула Мильтона Хара (2.44), которая при подстановке в нее зависимости (2.31) примет вид

												2
					1			R			Е	2
					1			R			Е
	z		р	1 exp						3	осн		.	(2.101)
			р	1 exp						3			.	(2.101)
		1			2			z			Е
					2		р	z	сл		Е
							р		сл		сл
Результаты расчета по формуле (2.101) приведены в табл. 2.18.
Таблица 2.18. Сопоставление результатов расчета напряжений по
формуле (2.101) при р=0,485 с данными эксперимента
Глубина,		Напряжение по оси симметрии нагрузки, кПа												Погреш-
Глубина,		измеренное				вычисленное					по	формуле		Погреш-
см		измеренное				(2.101) при Ещ/Егр=7								ность, %
						(2.101) при Ещ/Егр=7
0			329,6							329,6				0
5,0			319,4							325,35				-1,86
12,5			173,6							165,30				4,78
20,0			98,0							78,48				19,92
27,5			37,8							44,16				-16,82

Из анализа данных табл. 2.18 следует, что формула (2.101) позволяет получать удовлетворительные результаты расчета напряжения во всех точках слоя основания. Сравнивая результаты расчета напряже-

ний по формулам (2.99) при р=0,257 и (2.101) при р=0,485, пред-

ставленные в табл. 2.17 и 2.18, нетрудно заметить, что результаты

расчета практически одинаковы. Отсюда следует, что для этих зависимостей можно подобрать такие пары значений параметров р, при которых результаты расчета будут одинаковыми. Значит достаточно применять одну из этих формул (2.99) или (2.101).

Рассматривая возможность применения к расчету нормальных вертикальных напряжений зависимости М.П. Болштянского, отметим, что в формулах (2.49) и (2.50) величина постоянного коэффициента принята 2,25. Эта величина вычислена из формулы И.И. Кандаурова (2.43) при р=0,38. Так как нами установлено, что модель И.И. Кандаурова удовлетворительно описывает экспериментальные данные Брюса Даниеля Стивена при р=0,257, то в формуле М.П. Болштянского постоянный коэффициент 2,25 целесообразно заменить некоторой функцией bБ, зависящей от параметров текстуры, формы зерен каменного материала, гранулометрического состава смеси и показателей физических свойств. В этом случае формула (2.49) примет вид

									z	2 1
			z	р 1 b							.				(2.102)
				р 1 b							.				(2.102)
				1		Б		D

Подставив в выражение (2.102) зависимость (2.31), получим
формулу													1
												2
												2
							zсл				Есл
		р					zсл		3		Есл			.	(2.103)
		р							3					.	(2.103)
	z			1	Б		D
							D				Еосн

Результаты расчета напряжений по формуле (2.103) приведены в табл. 2.19.

Таблица 2.19. Сопоставление результатов расчета напряжений по

формуле (2.103) с данными эксперимента

	Напряжение по оси симметрии нагрузки,			Погрешность, %
Глубина,		кПа		Погрешность, %
		кПа
		вычисленное	по формуле
см		вычисленное	по формуле	при	при
см	измеренное	(2.103) при		при	при
	измеренное	(2.103) при		bБ =2,25	bБ =3,47
		bБ =2,25	bБ =3,47	bБ =2,25	bБ =3,47
		bБ =2,25	bБ =3,47
0	329,6	329,6	329,6	0	0
5,0	319,4	290,84	273,41	8,94	14,40
12,5	173,6	179,82	144,27	-3,58	16,89
20,0	98,0	105,22	76,86	-7,37	21,58
27,5	37,8	65,51	45,67	-73,30	-20,81

Примечание. При расчетах величина отношения Есл/Еосн принята соответствующей отношению измеренных модулей Ещ/Егр=7.

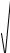
Из анализа данных табл. 2.19 следует, что зависимость (2.103) может быть принята для инженерных расчетов. Результаты расчета по формуле (2.103) приблизительно совпадают со значениями напряжений, вычисленных по формуле (2.98), но обе зависимости (2.98) и (2.103) дают погрешность больше, чем выражения (2.99) и (2.101).

Возможность применения для расчета вертикальных нормальных напряжений в сечении по оси симметрии нагрузки оценим сопоставлением экспериментальных данных с результатами расчета по классической формуле (2.52) или ее аналогу (2.53). Подставив в (2.50) зависимость (2.31) для сечения по оси симметрии нагрузки, получим формулу

						2 z								2
						2 z		сл		Е	сл			2
		z		р 1				сл	3		сл	tg		.		(2.104)
				р 1					3			tg		.		(2.104)
			1				D			Еосн
							D			Еосн
Результаты расчета напряжений по формуле (2.104) приведены в
табл. 2.20.
Таблица 2.20. Сопоставление результатов расчета напряжений по
формуле (2.104) с данными эксперимента
	Напряжение по оси симметрии нагрузки,														Погрешность, %
Глубина,					кПа										Погрешность, %
					кПа
					вычисленное по						формуле				при	при
см					вычисленное по						формуле
см	измеренное				(2.104) при
					(2.104) при										=20о	=36о
					=20		о			=36			о		=20о	=36о
					=20					=36
0	329,6				329,6					329,6					0	0
5,0	319,4				237,86					179,88					25,53	43,68
12,5	173,6				158,31					92,85					8,81	46,52
20,0	98,0				112,90					56,53					-15,20	42,31
27,5	37,8				84,55					38,00					-123,68	-0,5334

Из анализа данных табл. 2.20 следует, что формула (2.104) позволяет получать результаты, удовлетворительно согласующиеся с данными эксперимента только в некоторых точках слоя конечной толщины. Также следует отметить, что при должном подборе угла рассеивания напряжения можно практически точно рассчитать величину напряжения на нижней поверхности слоя в точке на оси симметрии нагрузки. Заметим, что все модели распределяющей способности разрабатывались для расчета напряжений в грунтовом полупространстве, а не в слое конечной толщины. Поэтому для окончательного суждения о применимости классической модели Е. Головачева (2.52) и ее модификаций необходимы эксперименты на грунтах.

Выполнив испытания дорожных конструкций, Б.Д. Стивен установил, что вертикальные напряжения, составляющие 5 % от напряжений под осью симметрии нагрузки, находятся на линии с некоторым

усредненным углом наклона 33 [116] (рис. 2.34).

Рис. 2.34. Экспериментальные данные рассеивания напряжений:

1 – экспериментальное местоположение точки с вертикальным напряжением 5 % от напряжения, возникающего под осью нагрузки на этой же глубине; 2 – рассеивание напряжений по Стивену и упрощенной модели;

3 – рассеивание напряжений по модели с разными углами рассеивания напряжений в слоях

На рис. 2.34 представлено рассеивание напряжений по глубине дорожной конструкции. Прямая 2 соответствует местоположению точек, в которых вертикальное нормальное напряжение составляет 5 % от напряжения, возникающего в точках, расположенных на этой же глубине в сечении по оси симметрии нагрузки. Измерение напряжений выполнено под одной шиной, площадь отпечатка которой составляет 225 243=264 мм2, а диаметр площадки нагружения равен 0,264 м. Отметим, что определяя угол наклона прямой, на которой напряжения составляют 0,05 от нормальных вертикальных напряжений, возникающих в точках, расположенных на этой же глубине, в сечении оси симметрии нагрузки

Б.Д. Стивеном допущена ошибка. Для пояснения этой ошибки приведем расстояния, указанные Б.Д. Стивеном, до точек, в которых измеренные вертикальные напряжения составляют приблизительно 5 % от напряжения по оси симметрии нагрузки.

Угол наклона прямой 2, показанной на рис. 2.34, определим из тригонометрии прямоугольных треугольников. Обозначив этот угол как угол рассеивания напряжения и применив тригонометрические соотношения для определения углов прямоугольных треугольников, получим

90 arctg	z	,	(2.105)

	X1

где X1 и z – абсцисса и ордината точки, указанные Б.Д. Стивеном и схематично показанные на рис. 2.27, в которых вертикальные нормальные напряжения составили 5 % от напряжений в сечении по оси симметрии нагрузки.

Результаты вычислений по формуле (2.105) приведены в табл. 2.21.

Таблица 2.21. Углы наклона прямых к точкам, в которых

вертикальные нормальные напряжения составляют 5 % от напряжений, возникающих в сечении по оси симметрии нагрузки

Номер станции		7	7	7	7	7	17	29	38
		Экспериментальные данные Б.Д. Стивена
Глубина	распо-
ложения	точки	0,075	0,150	0,225	0,300	0,375	0,225	0,225	0,300
Z, м
Удвоенное рас-
стояние Dz=2X1		0,525	0,525	1,075	1,075	1,3	1,025	0,875	1,3
от оси	симмет-
рии нагрузки, м
Диаметр	отпе-	0,264	0,264	0,264	0,264	0,264	0,264	0,264	0,264
чатка шины D, м		0,264	0,264	0,264	0,264	0,264	0,264	0,264	0,264
			Вычисленные данные
Расстояние		0,1305	0,1305	0,4055	0,4055	0,518	0,3805	0,3055	0,518
Х1=0,5·(Dz-D0), м		0,1305	0,1305	0,4055	0,4055	0,518	0,3805	0,3055	0,518
Угол , о		60,1	41	61	53,5	54,1	59,4	59,4	59,9

Из анализа данных табл. 2.21 следует, что действительные значения углов находятся в пределах 41 – 61о. Поэтому величина угла рассеивания не равна 33о, указанным Б.Д. Стивеном. Отметим, что если вместо диаметра отпечатка шины D=26,4 см принять диаметр отпечатка колеса D0=37,3 см, то за исключением второй точки стан-

ции №7 вычисленные значения углов рассеивания существенно превышают 33 о, указанные Б.Д. Стивеном. В этом случае средняя величина составляет 48,8 о.

Несмотря на обнаруженную ошибку, данные Б.Д. Стивена в определенной мере подтверждают модель распределяющей способности, но из анализа опытных данных, представленных на рис. 2.34, следует, что более точной является модель с разными углами рассеивания напряжений в различных слоях. Экспериментальные данные Б.Д. Стивена позволяют оценить достоверность предлагаемого нами способа расчета главных напряжений вне оси симметрии нагрузки, заключающегося во введении коэффициентов, рассчитываемых по формулам (2.91). Отметим, что Б.Д. Стивеном вне оси симметрии нагрузки измерены нормальные вертикальные напряжения, а формулы (2.91), (2.92) и (2.93) позволяют вычислять главные напряжения. Поэтому результаты расчета по этим формулам с данными эксперимента сопоставлять нельзя. Необходимо, используя предлагаемый способ расчета напряжений вне оси симметрии нагрузки, получить формулу для расчета нормального вертикального напряжения. Для этого воспользуемся решением Мичелла, которое представлено в табл. 2.3. Применяя формулу Мичелла для расчета вертикального нормального напряжения, в предлагаемом нами способе получим выражение для расчета коэффициента Kz. Этот коэффициент аналогичен коэффициентам К1 и К2, но в отличие от них позволяет вычислять не главные напряжения, а вертикальное нормальное напряжение вне оси симметрии нагрузки. Применив решение Мичелла, получим

Кz		в x;z sin	в x;z cos2	x;z	.	(2.106)
	в 0;z sin в 0;z cos2			0;z

Для оси симметрии нагрузки величина угла (0; z) составляет 0о, вследствие чего cos (0; z)=cos0=1. Поэтому формулу (2.106) целесообразно записать в виде

Кz	в x;z sin в x;z cos2 x;z	.	(2.107)
	в 0;z sin в 0;z

Подставляя зависимость (2.107) в любую из формул, предназначенных для расчета вертикального нормального напряжения в сечении по оси симметрии нагрузки, получим

z	р К	в x;z sin в x;z cos2 x;z	.	(2.108)
		в 0;z sin в 0;z

При выполнении расчетов величина углов (x; z) вычислялась по формуле табл. 2.4, предназначенной для расчета угла видимости в точках за пределами нагруженной площадки. Углы (x; z) определяются из тригонометрии прямоугольных треугольников, а именно

	x;z в x;z arctg X1					z.			(2.109)
Таблица 2.22. Экспериментальные данные и результаты расчета
относительной величины вертикальных напряжений
Номер станции		7	7	7	7		7	17	29	38
Глубина Z, м		0,075	0,150	0,225	0,300		0,375	0,225	0,225	0,300
Диаметр D0, м		0,264	0,264	0,264	0,264		0,264	0,264	0,264	0,264
, град		56,28	56,28	56,28	56,28		56,28	56,28	56,28	56,28
Dz=D0+2 Z tg		0,489	0,713	0,938	1,163		1,388	0,938	0,938	1,63
Dz по Стивену		0,525	0,525	1,075	1,075		1,3	1,025	0,875	1,3
Расстояние Х1, м,		0,112	0,225	0,337	0,449		0,562	0,337	0,337	0,449
Х1=0,5·(Dz-D0)		0,112	0,225	0,337	0,449		0,562	0,337	0,337	0,449
Х1=0,5·(Dz-D0)
Расстояние Х2,	м,	0,376	0,489	0,601	0,713		0,826	0,601	0,601	0,713
Х2= Х1+ D0
Угол в(x; z), рад		0,392	0,291	0,230	0,191		0,162	0,230	0,230	0,191
Угол в(0; z), рад		2,108	1,443	1,061	0,829		0,677	1,061	1,061	0,829
Угол (x;z), рад		1,178	1,128	1,098	1,078		1,063	1,098	1,098	1,078
Коэффициент Кz		0,041	0,045	0,05	0,055		0,060	0,050	0,050	0,055
Коэффициент Кz	по	0,05	0,05	0,05	0,05		0,05	0,05	0,05	0,05
Стивену		0,05	0,05	0,05	0,05		0,05	0,05	0,05	0,05
Стивену
( Кz), %		17,9	10,1	0	-9,9		-18,2	-0,24	-0,24	-9,9

Из анализа данных табл. 2.22 следует, что для всех точек измерения формула (2.107) дает удовлетворительные результаты.

Еще одним важным выводом, сделанным Б.Д. Стивеном, является зависимость горизонтального нормального напряжения от вертикального нормального напряжения. Этот вывод сделан на основе измерений напряжений в шести точках дорожных конструкций. Все точки расположены на одной глубине 75 см. В этих точках установлено два датчика давлений. Для измерения вертикальных напряжений датчики установлены горизонтально, а для измерения вертикальных напряжений датчики установлены вертикально. Сопоставляя данные эксперимента, Б.Д. Стивен пришел к выводу, что горизонтальное напряжение в этих точках составляет 12,5 % от вертикального нормального напряжения. Вследствие этого горизонтальное нормальное напряжение определяется по формуле [116, с. 111]:

x 0,125 z .

(2.110)

Б.Д. Стивен указывает на то, что соотношение напряжений, определяемое из (2.110), подобно результатам работы Р.Б. Фримена и М.Е. Хара, указавших на то, что соотношение горизонтального и вертикального нормальных напряжений в дробленом известняке составляет 0,14 [79]. Б.Д. Стивен [116], Р.Б. Фримен и М.Е. Хар [79] полагают, что вследствие подобия кривых уменьшения горизонтальных и вертикальных нормальных напряжений по глубине слоя их отношение практически не изменяется, вследствие чего может быть принято постоянным. В общем виде зависимость горизонтального нормального напряжения от вертикальной компоненты тензора напряжений можно представить формулой

x k z ,

(2.111)

где k – коэффициент, определяемый отношением горизонтального и вертикального напряжений, в рассматриваемой точке.

Сопоставляя предлагаемую в настоящей работе формулу (2.5) с

зависимостью (2.111), несложно получить равенство
k .			(2.112)
Аналогичное представление можно получить, рассматривая фор-
мулы (2.23) и (2.111):
k 1		.
	1 K2		(2.113)

Укажем, что в зависимости (2.111) постулируется постоянное, то есть не зависящее от глубины, значение коэффициента k, а в формулах (2.112) и (2.113) коэффициент k является функцией глубины. Таким образом, принципиальным отличием предлагаемого способа расчета минимального главного напряжения через величину максимального главного напряжения в сечении по оси симметрии нагрузки от способов Б.Д. Стивена [116], Р.Б. Фримен и М.Е. Хар [79] является зависимость коэффициента k от глубины. Отметим, что при увеличении глубины до некоторого значения величина коэффициента К в формуле (2.113) изменяется слабо, вследствие чего значение коэффициента k по глубине практически не изменяется.

Аналогичное мнению автора суждение о зависимости коэффициента k от глубины высказывается в различных работах. Обширный обзор таких работ применительно к горным породам выполнен в гл. 10 монографии Эверта Хоека [93]. Э. Хоек указывает, что изначально коэффициент k определялся как функция коэффициента Пуассона, а именно точно так же, как коэффициент бокового давления в формуле (2.3), то есть в соответствии с представлением К. Терцаги и Ф.Е. Ри-

харта [119]. Зависимость К. Терцаги и Ф.Е. Рихарта предполагает постоянное по глубине значение коэффициента k. Э. Хоек отмечает, что

внастоящее время представление Терцаги – Рихарта практически не применяется [93]. Это обусловлено появлением экспериментальных данных [72, 89], согласно которым коэффициент k является функцией глубины, что соответствует зависимостям (2.23) и (2.113).

Учитывая сделанные на основе сопоставления теоретических и экспериментальных данных выводы для расчета главных напряжений

вслоях дорожной одежды из дискретных материалов, можно рекомендовать четыре модели, представленные в табл. 2.23.

Таблица 2.23. Формулы для расчета главных напряжений в сечении по

оси симметрии нагрузки в слое из дискретных материалов

Модель

Формула

сл

р 1

;

Еосн

Модифицированная

сл

модель Лява – Фре-

р 1

лиха – Олсона –

R Е

осн

Одемарка

сл

1 1

R Е

осн

Есл

р 1 b

zсл

;

осн

Модифицированная

Есл

zсл

модель Болштян-

ского – Одемарка

Еосн

Есл

zсл

осн

Окончание табл. 2.23

1 exp 4

осн

;

Есл

zсл

R 3

Еосн

Модифицированная

1 exp 4

модель Кандаурова

Есл

zсл

– Одемарка

осн

1 exp 4 р

сл

1 exp

осн

;

сл

R 3

Еосн

Модифицированная

р 1 exp

модель Хара – Оде-

2 р

Есл

zсл

марка

осн

1 exp

сл

В модифицированных моделях табл. 2.23 максимальное главное напряжение определяется по оригинальным формулам, то есть зависимостям, полученным другими авторами, но с применением в них способа Н. Одемарка. Минимальное главное напряжение рассчитывается по формулам, полученным автором настоящей монографии, при помощи предлагаемого способа, который в математическом смысле формулируется выражением (2.23). Таким образом, модифицированные модели табл. 2.23 содержат новизну в формулах расчета минимального главного напряжения. Формулы, предназначенные для вычисления максимального главного напряжения, являются заслугой других специалистов – А. Лява, О.К. Фрелиха, Р.Е. Олсона, М.П. Болштянского, И.И. Кандаурова и М.Е. Хара, в которых применен способ Н. Одемарка. Из этого следует, что предлагаемый способ предназначен для модификации известных решений, в которых получены зависимости, позволяющие вычислять максимальное главное напряжение в сечении по оси симметрии нагрузки.

В грунте земляного полотна Б.Д. Стивен измерил вертикальное нормальное напряжение в сечении по оси симметрии нагрузки в двух точках. Одна точка расположена на поверхности, а вторая – на глубине 7,5 см. Это дает возможность сравнить экспериментальные данные с результатами расчета напряжений по различным формулам и сделать вывод о пригодности теоретических зависимостей для расчета максимальных главных напряжений по оси симметрии нагрузки в верхней части полупространства. Для расчета принят вычисленный в табл. 2.10 диаметр площадки, по которой нагрузка распределена по поверхности земляного полотна, и измеренное контактное давление

37,8 кПа.

Таблица 2.24. Сопоставление результатов расчета напряжений по формулам

А. Лява (табл. 1.1) и М.И. Якунина (2.28) с данными эксперимента Б. Стивена

	Нормальное вертикальное напряжение по			Погрешность, % по
Глубина,	оси симметрии нагрузки, кПа			формуле
см	измеренное	А. Лява	М.И. Якуни-	А. Лява	М.И. Яку-
			на		нина
0	37,8	37,8	37,8	0	0
7,5	36,7	37,72	37,65	-2,78	-2,57

Из анализа данных табл. 2.24 следует, что обе формулы для точки с относительной глубиной z/D=0,065 дают результаты, мало отличающиеся от данных эксперимента. Тем не менее в эксперименте измерено напряжение всего в одной точке, расположенной внутри земляного полотна. Вследствие этого делать вывод об адекватном расчете напряжений в других точках, расположенных ниже глубины 7,5 см, затруднительно. Кроме того, другие зависимости, включающие в себя параметр грунта, дают более точные результаты (табл. 2.25).

Таблица 2.25. Сопоставление результатов расчета напряжений по формуле

(2.35) и вычислении параметра n по формуле (2.37) с данными эксперимента

Глубина,	Нормальное вертикальное напряжение			Погрешность, % по фор-
см	по оси симметрии нагрузки, кПа			муле (2.35)
	измеренное	вычисленное по формуле
		(2.35) при:
		CBR=3,8 %	CBR=20 %	CBR=3,8 %	CBR=20 %
		n=1,715	n=3	n=1,715	n=1,3
0	37,8	37,8	37,8	0	0
7,5	36,7	36,701	37,72	0,04	-2,58

Втабл. 2.25 приведены результаты расчета нормальных вертикальных напряжений по формуле (2.35), в которой параметр Фрелиха вычислен по зависимости (2.37). Из анализа данных табл. 2.25 следует, что варьированием параметра Фрелиха можно добиваться практически полной сходимости результатов расчета и данных эксперимента. При этом возможность расчета параметра Фрелиха по формуле (2.37) вызывает сомнение. При реальной величине CBR грунта, равной 20 %, параметр Фрелиха n равен трем. В этом случае зависимость (2.35) дает такие же результаты, как и формула А. Лява (табл. 1.1). Для более точного расчета напряжений параметр Фрелиха необходимо уменьшить до 1,715, что имеет место при его вычислении по формуле (2.37) при величине CBR грунта равной 3,8 %. Такая малая величина калифорнийского числа несущей способности грунта характерна для слабых грунтов, например водонасыщенного суглинка. Влажность грунта на кольцевом стенде близка к его оптимальной влажности, вследствие чего величина CBR грунта не может быть меньше 10 – 20 %. Поэтому формула (2.37) не может применяться для расчета параметра Фрелиха.

Втабл. 2.26 приведены результаты расчета напряжений по формуле Лява – Фрелиха – Олсона (2.40).

Таблица 2.26. Сопоставление результатов расчета напряжений по

формуле (2.40) с данными эксперимента

Глубина,	Напряжение по оси симметрии нагрузки, кПа			Погрешность, %
Глубина,		вычисленное	по формуле	при n=3	при
см	измеренное	(2.40) при			n=2,25
		n=3	n=1,715
0	37,8	37,8	37,8	0	0
7,5	36,7	37,72	36,701	-2,58	0,04

Из анализа данных табл. 2.26 следует, что при одинаковой величине параметра Фрелиха результаты расчета напряжений по формулам (2.35) и (2.40) совпадают. В отличие от формулы (2.35) и (2.37) модель Лява – Фрелиха – Олсона не предполагает зависимости параметра Фрелиха от величины калифорнийского числа несущей способности грунта. Поэтому определение параметра Фрелиха в формулах (2.35) и (2.40) необходимо выполнять из экспериментальных данных, выполненных с различными грунтами и при различных физических характеристиках. Возможно, после таких испытаний удастся создать математическую модель зависимости параметра Фрелиха от CBR.

Анализ данных табл. 2.25 и 2.26 позволяет сделать вывод о том, что ввод в формулу А. Лява параметра Фрелиха позволяет повысить точность расчета напряжений в дорожной конструкции. Поэтому формулы механики сплошной среды, выведенные для расчета вертикальных нормальных напряжений, должны включать параметр материала.

В табл. 2.27 приведены результаты расчета нормальных вертикальных напряжений по формулам механики зернистой среды И.И. Кандаурова (2.43) и М. Хара (2.44).

Таблица 2.27. Сопоставление результатов расчета напряжений по

формуле (2.43) с данными эксперимента

	Напряжение по оси симметрии нагрузки,			Погрешность по фор-
Глубина,		кПа		муле, %
		вычисленное по формуле		(2.43) при	(2.44) при
см
	измеренное	(2.43) при	(2.44) при
				р =0,0148	р =0,845
		р =0,0148	р =0,845

0	37,8	37,8	37,8	0	0
7,5	36,7	36,7104	36,7086	-0,028	-0,23

Из анализа данных табл. 2.27 следует, что варьирование параметра р позволяет практически точно рассчитывать напряжение, но определение этого параметра требует измерения напряжений в существенно большем количестве точек по глубине земляного полотна по сравнению с числом измерений, выполненных Б.Д. Стивеном.

Формулу М.П. Болштянского представим в виде зависимости (2.102), в которой параметр bБ имеет произвольное значение. Результаты расчета напряжений по формуле (2.102) приведены в табл. 2.28.

Таблица 2.28. Сопоставление результатов расчета напряжений по

формуле (2.102) с данными эксперимента

	Напряжение по оси симметрии нагрузки,			Погрешность, %
Глубина,		кПа

		вычисленное	по формуле
см				при	при
	измеренное	(2.102) при
				bБ =2,25	bБ =7,18
		bБ =2,25	bБ =7,18

0	37,8	37,8	37,8	0	0
7,5	36,7	37,44	36,7004	2,04	-0,001

Из анализа данных табл. 2.28 следует, что при величине параметра bБ, равного 2,25, то есть значению, рекомендованному М.П. Болштянским, зависимость (2.102) позволяет получать более точные ре-

зультаты по сравнению с формулой А. Лява. Варьированием параметра bБ можно добиваться совпадения результатов расчета с данными эксперимента. Следовательно, значение параметра bБ может быть определено по экспериментальным данным.

В табл. 2.29 приведены результаты расчета напряжений по фор-

муле (2.52).

Таблица 2.29. Сопоставление результатов расчета напряжений по

формуле (2.52) с данными эксперимента

	Напряжение по оси симметрии нагрузки,			Погрешность форму-
Глубина,		кПа		лы (2.52), %
		вычисленное	по формуле	при	при
см
	измеренное	(2.52) при
				=6,56о	=20о
		=6,56о	=20о
0	37,8	37,8	37,8	0	0
7,5	36,7	36,7013	34,4808	-0,004	6,05

Из анализа данных табл. 2.29 следует, что подбором угла рассеивания напряжений можно добиваться сходимости результатов расчета и экспериментальных данных. При этом отметим, что практически полное совпадение результатов расчета имеет место при малом угле рассеивания напряжений. Для применения модели распределяющей способности к расчету напряжений необходимо разработать методику определения угла рассеивания напряжений.

Из сопоставления вычисленных и экспериментальных значений напряжений можно сделать вывод, что малое количество точек внутри земляного полотна, в которых Б.Д. Стивеном измерены напряжения, не позволяет выбрать модель, наиболее точно описывающую опытные данные. Вследствие этого для выбора модели расчета главных напряжений по оси симметрии нагрузки, распределенной по круглой площадке, необходим дополнительный анализ экспериментальных данных. При этом возможна прямая и косвенная оценки предлагаемых моделей. Прямой способ заключается в сравнении вычисленных максимальных и минимальных напряжений с их экспериментальными данными. Косвенный способ заключается в сравнении параметров напряженно-деформированного состояния земляного полотна, вычисленных с привлечением предлагаемых модифицированных моделей расчета главных напряжений, с измеренными значениями при постановке экспериментов. К таким косвенным характеристикам оценки моделей расчета напряжений можно отнести осадки зем-

ляного полотна или первую и вторую критические нагрузки Н.М. Герсеванова. Сопоставлением измеренных осадок или критических нагрузок с их вычисленными значениями при привлечении различных модифицированных моделей можно косвенно судить о точности формул расчета главных напряжений. В табл. 2.30 приведены предлагаемые формулы расчета главных напряжений в сечении по оси симметрии нагрузки, распределенной по круглой площадке, для каждой модифицированной модели.

Таблица 2.30. Формулы для расчета главных напряжений в грунтовом

полупространстве для сечения по оси симметрии нагрузки

Модель

Формула

1 р К ;

К 1

;

1 R/z 2 2

Модифицированная

р 1

модель А. Лява

1 R/z

1 1 1

R/ z 2 2

р К ;

сл

;

Еосн

2 1

Модифицированная

сл

3 р

1 а

модель М.И. Якунина

Еосн

2 2

1 1

сл

Еосн

Модифицированная

R 2

модель Лява – Фре-

1 р К ;

К 1

;

лиха

Продолжение табл. 2.30

3 р 1

Модифицированная

модель Лява – Фре-

лиха

R 2

1 1

1 р К ;

К 1

;

z n

Модифицированная

3 р 1

модель Лява – Фре-

лиха – Олсона

z n

1 1

р К ;

К 1 exp

;

Модифицированная

4 р R2

р 1 exp

модель И.И. Кандау-

рова

4 р R2

1 1 exp

р К ;

2 1

К 1 b

;

Модифицированная

модель М.П. Бол-

штянского

р 1 b

1 1 b

Окончание табл. 2.30

р К ;

К 1 exp

;

Модифициро-

р 1 exp

ванная модель

М. Хара

1 1 1 exp

Модифицированные модели распределяющей способности

1 р К ;

2 z

Модифицирован-

;

ная модель

2 z

Е. Головачева

2 z

Модифицирован-

1 р К ;

tg от .

ная модель Е. Го-

ловачева при

2 z

= от

р 1

tg от

Модифицирован-

2 z

р К ;

;

ная модель рас-

пределяющей

2 z tgf

способности при

=f( )

3 р 1

р К ;

2 z

;

Модифицирован-

ная модель рас-

2 z

пределяющей

способности при

2 z

1 1

Выводы по главе 2

1.Анализ решения А. Лява, применяемого для расчета главных напряжений в сечении по оси симметрии нагрузки, распределенной по круглой площадке, выявил его недостатки, которые приводят к тому, что вычисленные напряжения отличаются от измеренных в экспериментах. Эти недостатки состоят в том, что:

– на поверхности величина минимального главного напряжения превышает значение, при котором грунт испытывает компрессионное сжатие;

– на некоторой глубине минимальное главное напряжение меняет знак, то есть из сжимающего превращается в растягивающее;

– формула для расчета максимального главного напряжения не содержит параметров материала, вследствие чего на одной и той же глубине в различных материалах возникают одинаковые напряжения.

2.Модификация решения А. Лява выполнялась различными пу-

тями:

– в формулу максимального главного напряжения введен параметр Фрелиха;

– получены решения механики зернистой среды, базирующиеся на математической статистике, а не на дифференциально интегральном исчислении, как это принято в механике сплошной среды;

– инженерные решения, созданные на основе анализа физических моделей, к которым можно отнести воображаемую модель распределяющей способности и натурные модели, в которых измеряются напряжения. В результате получены аналитические и эмпирические формулы.

3.Выполнен анализ решений, в которых предприняты попытки определения минимального главного напряжения как доли от максимального. Недостатком таких решений является постоянное по глубине значение коэффициента пропорциональности.

4.Перечисленные в п. 1 – 3 недостатки побудили нас разработать способ расчета минимального главного напряжения. Формула для расчета минимального главного напряжения должна удовлетворять следующим условиям:

– В сечении по оси симметрии нагрузки на поверхности полупространства возникает компрессионное сжатие, то есть при z=0 главные

деформации 2= 3=0, а главные напряжения 2= 3= 1/(1- ).

–При изменении глубины в пределах 0<z< грунт работает в условиях трехосного сжатия 2= 3< 1/(1- ), испытывая деформации бокового расширения 2= 3<0.

–По оси симметрии нагрузки в точке z= грунт испытывает од-

ноосное сжатие 2= 3=0 и 2= 3=- 1.

Решение, удовлетворяющее этим условиям, найдено в виде формулы (2.5), представляющей собой модификацию известной в механике грунтов формулы для расчета минимального главного напряжения, при возникновении которого грунт (материал) работает в условиях компрессионного сжатия. Модификация выполнена вводом в из-

вестную формулу коэффициента (альфа), представляющего собой непрерывную по глубине функцию. Для определения изменения величины этого коэффициента по глубине получена математическая связь коэффициента с известным в механике грунтов коэффициентом бокового обжатия . Используя представление Федоровского – Безволева, описывающее непрерывное изменение коэффициента по глубине, нами получено неразрывное решение для . Согласно этому решению на поверхности при z=0 =1, а минимальное главное напряжение определяется произведением максимального главного напряжения и коэффициента бокового давления, вследствие чего2= 3=0, то есть грунт работает в условиях компрессионного сжатия. В точке на бесконечности z= =0 и 2= 3=0, вследствие чего 2= 3=-1, то есть грунт испытывает одноосное сжатие. Во всех остальных точках полупространства 0<z< 1< <0, вследствие чего 2= 3= 1, то есть грунт испытывает осевое трехосное сжатие.

5.Полученное решение в виде неразрывной по глубине функции

позволило модифицировать модели расчета главных напряжений, возникающих в сечении по оси симметрии нагрузки, распределенной по круглой площадке так, чтобы максимальное главное напряжение определялось по оригинальной формуле, а минимальное главное напряжение рассчитывалось по новому способу. В каждой модифицированной модели минимальное главное напряжение по глубине затухает более интенсивно по сравнению с максимальным главным напряжением, вследствие чего с увеличением глубины стесненность боковых деформаций расширения уменьшается.

6.Сопоставление результатов расчета напряжений с экспериментальными данными позволило выявить наиболее достоверные модели и рекомендовать их для расчета главных напряжений.

3. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ УГЛА РАССЕИВАНИЯ НАПРЯЖЕНИЙ В ГРУНТАХ

Б.С. Радовский сообщает, что модель распределяющей способности предложена Е. Головачевым в 1870 г. [50].

В основу предложения Е. Головачева положена воображаемая физическая модель, в соответствии с которой рассеивание напряжений по глубине происходит под некоторым углом. В связи с этим при увеличении глубины площадь передачи нагрузки возрастает

(рис. 3.1) [17, 117].

Нормальное верти-

Рис. 3.1. Схема рассеивания вертикального кальное напряжение,

нормального напряжения [17, 117]	которое по оси сим-

метрии нагрузки равно максимальному главному напряжению, определяется отношением усилия, передаваемого на поверхность дорожной конструкции и площади распределения этой нагрузки на рассматриваемой глубине.

Экспериментальные данные показывают, что распределяющая способность слоя дорожной одежды или земляного полотна зависит от вида материала или грунта, а также показателей физических свойств. Поэтому угол рассеивания напряжений является параметром материала и различен в слоях из различных материалов.

Несмотря на достаточно простые представления о распределении напряжения по глубине слоя, модель распределяющей способности за рубежом пользуется определенной популярностью. Это связано с необходимостью расчета грунтов земляного полотна и оснований фундаментов, армированных геосинтетическими материалами. В этих расчетах предполагается, что укладка геосинтетического материала приводит к увеличению угла рассеивания напряжений под армирующей сеткой [103, с. 26]. Для практического применения этой модели

разработаны различные способы определения угла рассеивания напряжений через другие параметры материала: угол естественного откоса [50], сопротивление недренированному сдвигу [74, 100, 103].

Таким образом, известные методы определения угла рассеивания напряжения являются косвенными. В связи с этим разработка экспериментальной методики, позволяющей вычислять угол рассеивания напряжений по результатам исследований распределяющей способности, является актуальной задачей.

Экспериментальное исследование распределяющей способности и вычисление угла рассеивания напряжения могут быть реализованы при помощи метода цветных полос (рис. 3.2).

Рис. 3.2. Испытание песчаного основания методом цветных полос:

а – общий вид линий скольжения в песчаном основании [36, с. 64]; б – схема к определению угла рассеивания напряжений из тригонометрии прямоугольных треугольников (треугольник построен от начальной поверхности)

На рис. 3.2, а представлен общий вид модели песчаного основания с поверхностями скольжения, образовавшегося после вдавливания в него модели ленточного фундамента [36, с. 64]. На этом рисунке стрелкой показана одна из двух интересующих нас линий разрыва цветных полос. На рис. 3.2, б построен прямоугольный треугольник, гипотенуза которого проходит по линии разрыва. Угол рассеивания напряжений определяется из тригонометрии прямоугольных треугольников, согласно которой тангенс этого угла равен отношению противолежащего катета b к прилежащему катету z. Отметим, что схема, представленная на рис. 3.2, б, может быть уточнена. Необходимость уточнения обусловлена тем, что в процессе вдавливания штампа угол рассеивания изменяется. Вследствие этого для повыше-

<<< < Предыдущая 12 / 62 3 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.202117.79 Mб42559.pdf
#
07.01.2021374.85 Кб5256.pdf
#
07.01.202117.98 Mб212560.pdf
#
07.01.202117.98 Mб622561.pdf
#
07.01.202118.09 Mб2592562.pdf
#
07.01.202118.1 Mб182563.pdf
#
07.01.202118.2 Mб562564.pdf
#
07.01.202118.65 Mб132565.pdf
#
07.01.202118.84 Mб482566.pdf
#
07.01.202119.12 Mб222567.pdf
#
07.01.202119.8 Mб552568.pdf