
- •ВВЕДЕНИЕ
- •1.2. Структура асфальтобетонной смеси
- •1.3. Свойства асфальтобетонных смесей
- •1.4. Хранение смесей в накопительном бункере
- •1.5. Транспортирование асфальтобетонных смесей
- •1.6. Загрузка смеси в кузов
- •1.7. Причины температурной сегрегации
- •1.8. Защита смеси от погодных воздействий
- •Контрольные вопросы
- •2.1. Статическое уплотнение
- •2.2. Трамбование
- •2.3. Виброуплотнение
- •Контрольные вопросы
- •3.1. Методы описания уплотнения асфальтобетонных смесей
- •Контрольные вопросы
- •4.1. Исследование изменения модуля деформаций
- •Контрольные вопросы
- •5. УКЛАДКА АСФАЛЬТОБЕТОННЫХ СМЕСЕЙ
- •5.1. Классификация асфальтоукладчиков
- •5.2.1. Технологическая схема асфальтоукладчика
- •5.2.2. Толкающие ролики
- •5.2.3. Бункер
- •5.2.4. Питатель
- •5.2.5. Распределитель асфальтобетонной смеси
- •5.2.6. Рабочие органы
- •5.2.7. Система подогрева
- •5.3. Основные параметры трамбующего бруса
- •5.4. Основные параметры вибрационных плит
- •5.6.1. Скорость укладки
- •5.6.3. Одновременная укладка двух слоёв
- •Контрольные вопросы
- •6. МАШИНЫ ДЛЯ УПЛОТНЕНИЯ
- •6.1. Общая классификация дорожных катков
- •6.2.2. Основные параметры катков статического действия
- •6.3.1. Классификация вибрационных катков
- •6.6. Классификация вибровозбудителей
- •6.7. Расчет вибровозбудителей
- •6.8. Расчёт на прочность основных узлов дорожного катка
- •6.8.1. Расчёт элементов рулевого управления
- •6.9. Тяговый расчёт
- •6.10. Выбор двигателя
- •6.11. Автоматизация дорожных катков
- •Контрольные вопросы
- •ЗАКЛЮЧЕНИЕ
Контрольные вопросы
1.Сущность процесса уплотнения.
2.Статическое уплотнение.
3.Характеристика уплотнения вибрацией.
4.Уплотнение трамбованием.
5.Достоинства виброуплотнения.
6.Сравнение уплотнения вибрацией и трамбованием.
7.Причины эффективного применения пневмошинных вальцов.
8.Когда процесс уплотнения считается завершённым?
9.Влияние изменения плотности дорожно-строительных материалов на его эксплуатационные свойства.
10.Принципиальные схемы вибрационных плит.
35
3. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ПРОЦЕССА УПЛОТНЕНИЯ
3.1.Методы описания уплотнения асфальтобетонных смесей
Вдостижении эффективности процесса уплотнения решающее значение оказывает соответствие параметров уплотняющего оборудования изменяющимся прочностным показателям уплотняемого материала.
К основным факторам, влияющим на процесс уплотнения, относятся:
физико-механические свойства материала;
конструктивные параметры рабочих органов;
режимы работы уплотняющих машин.
Физико-механические свойства асфальтобетонных смесей представлены модулем деформаций, вязкостью, пределами текучести и прочности и т.д. Их сочетание определяет более сложные свойства – релаксацию напряжений, ретардацию деформаций и др.
Сочетание трёх групп факторов обуславливает рациональность конструкции уплотняющего оборудования и эффективность процесса уплотнения. Основы взаимодействия уплотнителей с конгломератными материалами базируются на результатах экспериментальнотехнических исследований [7, 9, 11, 30, 39, 40, 44].
Под многократным воздействием уплотняющих средств смесь деформируется за счёт взаимного перемещения минеральных частиц, их сближения и плотной упаковки. При этом с каждым силовым воздействием её плотность увеличивается и соответственно возрастает её сопротивление деформированию.
Асфальтобетонные смеси являются упруговязкопластичными материалами. В зависимости от состояния и условий деформирования в них могут проявляться преимущественно упругие свойства, вязкопластичные или (в большинстве случаев) совокупность указанных свойств. В зависимости от проявления тех или иных свойств к асфальтобетонным смесям применимы законы, вытекающие из теории упругости или теории пластичности (ползучести).
Для определения максимальных напряжений под вальцом (рис. 3.1) с учётом свойств уплотняемого материала и параметров катка Н.Я. Хархута предложил зависимость [44]
36

max |
|
QE |
, |
(3.1) |
|
||||
|
|
BR |
|
|
где Q – вес вальца, Н; Е модуль деформаций материала, Па; В – ширина вальца, м; R – радиус вальца, м.
Формула позволяет определять геометрические размеры вальцов катка для любой стадии процесса уплотнения, что очень важно, но пользоваться ей на практике затруднительно, т.к. в литературе отсутствуют данные по изменению значений модуля деформаций материалов и необходимых контактных давлений в процессе укатки.
Для определения необходимого числа проходов Н.Я. Хархута вывел формулу [44]
1,3 |
|
Е |
|
|
|
||
|
|
|
|
||||
lgn |
|
|
|
, |
(3.2) |
||
|
n |
1 |
|||||
|
К |
|
|
|
|
||
где наименьшая относительная пластическая деформация; коэффициент, учитывающий долю пластической деформации в общей деформации; n контактные давления катка в последнем, n-м проходе, Па.
М.П. Костельов внёс дополнение в формулу (3.1):
max рЕ , |
(3.3) |
где р – показатель силового воздействия вальца на покрытие, Па,
p |
Q |
. |
(3.4) |
|
|||
|
BR |
|
|
Выбор типа катка рекомендуется производить, используя показатель р, значения которого приводятся в работе [25].
37
Основной целью уплотнения асфальтобетонных смесей является достижение плотной, компактной упаковки минеральных компонентов с целью достижения заданных физико-механических показателей асфальтобетонного покрытия. Асфальтобетонная смесь в начале процесса уплотнения представляет собой рыхлую среду с произвольно ориентированными минеральными частицами (щебень) и агрегатами (асфальтовяжущее и мелкий щебень), покрытыми битумными плёнками [40]. Конечная плотность асфальтобетонной смеси достигается в результате многократного приложения уплотняющей нагрузки с переориентацией минеральных частиц и формированием прочной и устойчивой структуры.
По мере уплотнения сопротивление смеси деформированию постоянно увеличивается в связи с ростом её плотности и остывания. Кроме того, его значения зависят от скорости деформирования и частоты приложения уплотняющий нагрузки. При различных сочетаниях условий уплотнения асфальтобетонная смесь может проявлять свойства как твёрдого, так и жидкого тела.
В процессе уплотнения можно выделить два этапа – начальный и основной [40].
На начальном этапе уплотнения (коэффициент уплотнения 0,7–0,92) минеральные зёрна смеси имеют небольшое количество контактов между собой, осуществляющихся через толстые прослойки асфальтовяжущего. Смесь в этот период подвижная и обладает малым сопротивлением деформированию. Поэтому в ней развиваются в основном остаточные (вязкопластические) деформации, упругие деформации практически отсутствуют. По мере роста плотности и снижения температуры смеси соотношение между упругими и вязкопластическими деформациями изменяется.
На основном этапе (kу = 0,92–1,0) активно формируется структураасфальтобетона,минеральные зёрна заполнителясближаютсядруг с другом, образуя большее количество точек соприкосновения (контактов). При этом толщина прослоек асфальтовяжущего уменьшается. При дальнейшем уплотнении образуется максимальное количество контактов, которые способствуют устойчивому закреплению зёрен в структуре материала. Сопротивление деформированию увеличивается. Смесь проявляет вязкоупругие свойства.
Каждое силовое воздействие вызывает в уплотняемой среде деформацию , которая складывается из двух составляющих: обратимой у и необратимой н [40]:
у н. |
(3.5) |
38
Соотношение у и н в процессе уплотнения непрерывно изменяется в связи с уменьшением температуры и ростом плотности смеси: значения у увеличиваются, н – уменьшаются.
В зависимости от величины и времени силового воздействия на смесь, а также скорости деформирования в асфальтобетонной смеси будут проявляться в разной степени упругие, упругопластичные, упруговязкие или вязкопластичные составляющие деформации.
Результаты исследований [39] показывают, что для эффективного уплотнения асфальтобетонных смесей необходимо, чтобы возникающие под рабочими органами уплотняющих средств контактные давления к были не меньше предела текучести т уплотняемой среды, но не больше её предела прочности пр [44]:
т |
к пр. |
(3.6) |
Перемещение катка по |
уплотняемому слою |
производит его |
деформирование пропорционально величине действующих контактных давлений к. Поскольку величина к в процессе взаимодействия вальца с уплотняемой средой постоянно изменяется от нуля до максимума, то целесообразно в расчётах пользоваться средней
величиной контактного давления ср, Па. |
Значения ср можно |
||||
определить по формуле [40] |
|
mg |
|
|
|
ср |
|
, |
(3.7) |
||
|
|||||
|
|
BLab |
|
||
где Lab – длина горизонтальной проекции дуги контакта вальца и уплотняемой поверхности, м (рис. 3.2).
Возникающее напряженно-деформированное состояние смеси характеризуется скоростью изменения напряжённого состояния , Па/с, которое зависит от времени действия контактных давлений:
|
|
|
ср |
, |
(3.8) |
|
|||||
|
|
tд |
|
||
где tд время действия контактных давлений на уплотняемую среду,с. Чем выше значение tд, тем больше в уплотняемой среде успевает образоваться вязкопластических (остаточных) деформаций. Значение tд в процессе уплотнения постоянно уменьшается, а к, наоборот, увеличивается в связи с уменьшением пятна контакта вальца с
уплотняемой поверхностью.
Время действия вальца на асфальтобетонную смесь можно определить по формуле (см. рис. 3.2)
39

tд |
|
Lab |
, |
(3.9) |
|
||||
|
|
k |
|
|
где k – скорость перемещения вальца, м/с; Lab – горизонтальная проекция длины дуги контакта вальца и слоя смеси, м.
С ростом плотности и остыванием слоя смеси сопротивление деформированию увеличивается и соответственно уменьшается длина дуги контакта. Для расчёта длины дуги применяются различные
|
способы расчёта. |
|
|
||
|
Для решения конкретных задач |
||||
|
по эффективному уплотнению ас- |
||||
|
фальтобетонных смесей необходимо |
||||
|
иметь |
уравнение, |
связывающее |
||
|
между собой напряжения и дефор- |
||||
|
мацию. Так как развитие остаточной |
||||
|
деформации существенно зависит от |
||||
|
величины контактных давлений к, |
||||
|
их времени действия и скорости |
||||
|
деформирования, то в зависимость |
||||
Рис. 3.2. Схема перемещения |
должны |
входить |
tд |
и параметры, |
|
характеризующие |
упруговязкопла- |
||||
вальца: k – скорость катка; Gв – вес |
|||||
вальца; Lab – длина горизонтальной |
стичные свойства смеси. |
||||
проекции дуги контакта вальца |
Режим уплотнения, который |
||||
|
создаёт |
такое напряжённо-дефор- |
|||
мированное состояние в смеси, в результате действия которого возникают и развиваются максимальные остаточные деформации, считается эффективным. В этом случае повышается производительность уплотняющих средств и снижается энергоёмкость процесса.
Наиболее полно учесть развитие напряжённо-деформированного состояния асфальтобетонной смеси при уплотнении можно методами реологии, рассматривающей общие законы деформирования материалов во времени. Изучение существующих теорий [39, 40, 42] показало, что для изучения напряжённо-деформированного состояния среды наиболее пригоден модельный метод анализа. Используя этот метод, составляют дифференциальные уравнения, описывающие напряжения и деформации во времени. Эти уравнения решают в зависимости от условий, в которых будет находиться материал при воздействии на него рабочего органа. В структурных моделях свойства реального материала описываются аналогами механических тел, уже имеющих уравнения состояния. Структурные модели хорошо зарекомендовали
40
себя при описании напряжённо-деформированного состояния материалов, имеющих композиционное, органическое или полимерное строение при рассмотрении процессов их структурообразования, например в пищевой или нефтяной промышленности.
Применение реологических моделей позволяет прогнозировать накопление остаточных деформаций при различных условиях нагружения. Модельный метод анализа позволяет значительно уменьшить объём лабораторных исследований при выборе параметров рабочего оборудования и рассмотреть различные его сочетания. Учёт изменяющихся свойств смеси в процессе уплотнения значительно повышает точность этого метода.
3.2. Реологическая модель процесса уплотнения асфальтобетонной смеси катками статического действия
Требования к реологической модели, описывающей развитие напряженно-деформируемое состояние асфальтобетонной смеси в процессе уплотнения, можно сформулировать в следующем виде [39]:
асфальтобетонная смесь является вязкопластической сжимаемой средой;
необратимые деформации являются вязкопластическими;
на начальном этапе уплотнения упругие деформации пренебрежимо малы при уплотнении катками статического действия;
модель должна обладать упруговязкопластичными свойствами;
напряжения релаксируют по определённому закону;
суммарная деформация растёт до конечного значения;
при разгрузке наблюдается частичное восстановление упруговязкопластичных деформаций;
с ростом плотности в материале меняется соотношение между обратимыми и необратимыми деформациями.
Реологические модели, с одной стороны, должны быть более просты по своей структуре, что даёт возможность описать их поведение несложными дифференциальными уравнениями, и, с другой стороны, полнее отображать свойства уплотняемого материала (упругость, вязкость, пластичность) и явления, происходящие в нём (релаксация напряжений, ретардация деформаций).
Вработе [40] существует много предложений по описанию реологических процессов. Они моделируются с помощью фундаментальных реологических моделей, описывающих какое-либо
41

одно свойство (рис. 3.3): упругость [тело Гука (Н)], вязкость [тело Ньютона (N)], пластичность [элемент Сен-Венана (StV)].
Рис. 3.3. Фундаментальные реологические модели: а – модель Гука (Н); б – модель Ньютона (N); в – модель Сен-Венана (StV); Е– модуль упругости модели Гука (Н); – вязкость модели Ньютона;0 – предел текучести модели Сен-Венана.
Модель тела Гука описывает идеально твёрдую среду. Деформации, возникающие под действием нагрузки, полностью обратимы, т.е. мгновенно исчезают при снятии нагрузки и не зависят от времени действия нагружения.
Уравнение деформирования представлено законом Гука:
Е , (3.10)
где – напряжение, Па; Е – модуль упругости тела Гука, Па; – относительная деформация.
Модель вязкой жидкости Ньютона описывается уравнением
|
d |
, |
(3.11) |
|
|||
|
dt |
|
|
где – вязкость, Па с; t – время.
Деформации в жидкости, развивающиеся под действием нагрузки, необратимы. Из уравнения (3.11) видно, что величина деформации зависит от времени действия нагрузки.
Идеальное пластическое тело описывают моделью Сен-Венана. Деформация этой среды ограничена условием – при напряжении, меньшем предела текучести 0, тело не деформируется, при достижении этого напряжения происходит необратимое течение. Фундаментальные модели описывают идеальные тела и поэтомумогут использоваться только для описания простых свойств сложных материалов.
Для более подробного исследования реальных физических тел используются двухэлементные реологические модели (рис. 3.4, а, б, в): Прандтля (Pr = H–StV), Кельвина–Фойгта (F = H/N), Максвелла (M = = H–N). Эти модели позволяют рассмотреть сложные реологические
42

свойства – релаксацию напряжений, замедленное развитие деформаций, ретардацию деформаций и др. Однако при изучении процесса уплотнения двухэлементные модели не дают достаточно точного описания даже качественно, поэтому приходится применять более сложные модели.
Рис. 3.4. Сложные реологические модели: а – модель Максвелла; б – модель Кельвина–Фойгта; в – модель Прандтля; г – модель Бингама; д
– модель «стандартного» тела; е – модель Джеффриса; ж – модель Бюргерса; з – модель Шведова; и – модель Богуславского
Стремясь расширить диапазон отражаемых свойств, при которых модель способна достоверно описывать деформацию реального тела, исследователи применяют различные приёмы. Одним из таких приёмов является переход от сложных механических тел к спектральным или лестничным механическим моделям, представляющим соединение ограниченного или неограниченного количества
43

сложных тел (см. рис. 3.4, г–к): спектральные модели Фойгта (Fсп= |
||||||||
=F1–F2–…–Fn), Максвелла (Мсп=М1–М2–…–Мn), Феддера и Бредза [Fed |
||||||||
and Br = K–(Mur and Sch)1–…–(Mur and Sch)n] и т.д. |
|
|
|
|||||
Преследуя цель ещё больше расширить диапазон изменения |
||||||||
деформаций, исследователи вводят в механическую модель тела, |
||||||||
нелинейно деформируемые относительно величины напряжений, или |
||||||||
переходят к рассмотрению структурных моделей. В такие модели |
||||||||
включают определённое сопротивление, указывающее величину |
||||||||
напряжений, при которых деформация развивается по определённому |
||||||||
закону. |
|
|
|
|
|
|
|
|
Следует отметить, что введение большого количества |
||||||||
структурных сопротивлений в асфальтобетонных смесях приводит к |
||||||||
значительным трудностям при их экспериментальном определении. |
|
|||||||
В настоящей монографии принята реологическая модель, |
||||||||
объединяющая модель [40] и модель Джеффриса. Формула модели – |
||||||||
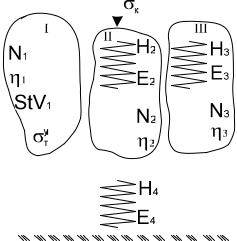
StV1 – ((N1||StV2) – (H||N2)). На рис. 3.5 приведён механический аналог |
||||||||
|
|
|
|
предлагаемой модели. |
|
|
||
|
|
к |
|
Модель |
состоит |
|
из |
|
|
|
|
|
|
||||
|
н |
StV1 |
|
элемента StV1 |
и двух блоков: I и |
|||
|
ту |
|
||||||
|
|
|
|
II. В процессе нагружения блок I |
||||
|
|
|
E |
учитывает необратимые дефор- |
||||
|
|
|
мации при напряжениях больше |
|||||
|
|
|
H |
|||||
N1 |
|
|
предела текучести и релаксацию |
|||||
|
|
|
напряжений в блоке II (элемент |
|||||
StV2 |
|
|
||||||
|
N2 |
Максвелла H||N2). Элемент StV1 |
||||||
|
0 |
|
||||||
|
ту |
|
|
учитывает |
необратимое дефор- |
|||
|
|
|
|
мирование |
начального |
этапа |
||
Рис. 3.6. Реологическая модель процесса |
деформирования, по истечении |
|||||||
уплотнения асфальтобетонной смеси |
которого |
он |
выключается |
из |
||||
|
|
|
|
работы. |
|
|
|
|
При приложении напряжений больше предела текучести дефор- |
||||||||
мируются элементы StV2 – ( H||N2) и модель врежиме установившегося |
||||||||
течения. Скорость течения определяется вязкостью смеси. Вязкий |
||||||||
элемент N1 |
при этом не работает, т. к. деформируется элемент |
StV2. |
||||||
Тело Сен-Венана определяет необратимую деформацию, а элемент |
||||||||
Максвелла |
(N H2) |
отрелаксировавшие и |
неотрелаксировавшие |
|||||
напряжения. |
|
|
|
|
|
|
|
|
Изменение напряжённо-деформированного состояния смеси во |
||||||||
время разгрузки описывается формулой с набором элементов N1 – |
||||||||
(H||N2). Деформация восстанавливается за счёт обратимой составля- |
||||||||
|
|
|
44 |
|
|
|
|
|
ющей полной деформации. Скорость восстановления определяется вязкостью упругого последействия. Одновременно с восстановлением деформаций происходит релаксация напряжений во втором блоке.
В случае приложения к модели нагрузки с высокой скоростью элементы StV2 – N деформируются, и если внутренние напряжения не успевают отрелаксировать (элемент Максвелла), то в среде развиваются значительные внутренние сопротивления, обусловленные замедленным перемещением вязких элементов Ньютона. В результате доля необратимых деформаций сокращается.
При составлении реологической модели процесса уплотнения асфальтобетонной смеси были приняты следующие допущения [40]:
асфальтобетонная смесь – упруговязкопластическая однородная сжимаемая среда;
стационарность процесса уплотнения;
рассматривается плоская одномерная задача;
толщина уплотняемого слоя находится в пределах активной зоны уплотнения;
уплотнение происходит в результате воздействия нормальных нагрузок, возникающих от вальца катка.
Первое допущение принято по следующим причинам:
во-первых, асфальтобетонная смесь принадлежит к коагуляционным материалам, составляющие которого (битум) обладают сильно выраженными упруговязкими свойствами [42];
во-вторых, проявление пластических и упруговязких свойств зависит от соотношения между временем действия нагрузки,временем последействия и количества нагружений [10, 25].
Второе допущение: стационарность процесса уплотнения – рассматривается установившийся процесс работы катка. При этом каток постоянно движется в заданном режиме (скорость постоянная), переходный процесс не учитывается.
Третье допущение – рассматривается одномерная задача, так как протяжённостьрабочихоргановуплотняющихмашиннамного больше длины зоны контакта вальца катка.
Четвёртое допущение связано с тем, что наиболее равномерное накопление деформаций происходит в пределах толщины слоя покрытия, называемой активной зоной уплотнения [22, 44]. Работа уплотняющих машин эффективна при толщине слоя, соответствующего активной зоне уплотнения. Увеличение толщины уплотняемого слоя требует применения уплотняющих машин, параметры которых отли-
45
чаются от большинства существующих машин. В тонких слоях, в свою очередь, большое влияние на сопротивление уплотнению оказывает прочность минерального заполнителя. В данной работе рассматриваются слои покрытия стандартной толщины 50–70 мм, уплотнение которых осуществляется большинством существующих машин.
При перемещении вальца послою уплотняемого материала валец создаёт в нём нормальные (от массы катка) и касательные (от силы тяги) напряжения. В настоящее время недостаточно изучено влияние касательных напряжений на интенсивность уплотнения, хотя установлено, что основное влияние на рост необратимых деформаций оказывают нормальные напряжения. Поэтому принято пятое допущение: уплотнение материала происходит в результате воздействия нормальных напряжений.
Рассмотрим работу модели на различных этапах уплотнения. 1. Начальный этап уплотнения.
При действии напряжений нm к пр в уплотняемой среде накапливаются необратимые деформации прямо пропорционально приложенному напряжению. Затухание их обуславливается упрочнением формирующейся структуры среды за счёт роста её плотности и понижения температуры. Необратимое деформирование отображается телом Сен-Венана StV1. Реологическое уравнение состояния среды представлено выражением
|
1 |
|
к , |
(3.12) |
|
||||
|
k |
|
|
|
где k коэффициент пропорциональности, Па.
Значение коэффициента пропорциональности определяется скоростью деформирования, температурой и плотностью смеси.
При дальнейшем уплотнении сопротивление деформированию увеличивается. Смесь сильнеепроявляетвязкоупругиесвойства.Когда сопротивление смеси увеличивается настолько, что пропорциональность между приложенной нагрузкой и развивающейся деформацией нарушается, начальный этап уплотнения завершается и элемент StV1 замыкается. Обычно это состояние смеси характеризуется коэффициентом уплотнения kу=0,90 – 0,92.
В случае предварительного уплотнения асфальтобетонной смеси оборудованием асфальтоукладчика анализ напряжённо-деформиро- ванного состояния асфальтобетонной смеси начинается сразу с основного этапа.
2. Основной этап уплотнения.
46

На основном этапе начинает активно деформироваться структураасфальтобетона,минеральные зёрна заполнителясближаютсядруг с другом, образуя большее количество точек соприкосновения (контактов). При этом уменьшается пористость и повышается плотность растворной части, образуется максимальное количество контактов, которые способствуют устойчивому закреплению зёрен в структуре материала.
Основной этап уплотнения характеризуется условным пределом текучести m, который определяет верхнюю границу контактных напряжений, при которых смесь проявляет свойства физически линейного упруговязкопластичного тела.
При условии m к пр полная деформация будет определяться упругопластической и вязкопластической составляющими. Механической моделью, отображающей подобное поведение реологически сложного материала при нагрузке, служит тело с формулой StV2– (H N2), являющееся усечённой моделью Шведова и не учитывающее мгновенные обратимые деформации.
Для составления дифференциального уравнения состояния модели при напряжении больше предела текучести удобно воспользоваться методом передаточных функций. Этот метод предполагает наличие причины – входной величины и следствия – выходной величины. Используя оператор Лапласа p=d/dt, можно упростить математические преобразования при выводе формул. Принимая за входную величину деформацию, передаточные функции модели Гука и Ньютона записываются в следующем виде [40]:
WH p |
|
|
|
1 |
; |
|
(3.13) |
|||||
|
|
|
|
|
|
|
||||||
к |
||||||||||||
|
|
|
E |
|
||||||||
|
|
|
|
|
|
|
1 |
, |
|
|||
WN p |
|
|
(3.14) |
|||||||||
|
|
|
|
|
|
|||||||
к |
||||||||||||
|
2 p |
|
||||||||||
где WH(p), WN(p) – передаточные функции элементов Гука и Ньютона;– деформация, преобразованная по Лапласу; k – напряжение, преобразованное по Лапласу.
Передаточная функция элемента Сен-Венана WStV(p) представлена в виде
WStV |
p |
|
|
к |
|
|
т |
. |
(3.15) |
||
|
|
|
|
|
|
||||||
|
|
||||||||||
|
|
|
|
||||||||
Суммируя WH p и WN p , получим передаточную функцию элемента Максвелла WM(p) [40]:
47

WM p |
|
|
|
|
|
|
WH p WN p , |
(3.16) |
||||||
|
|
|
|
|
||||||||||
к |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
WM p |
|
|
|
|
|
|
|
|
p 1 |
. |
(3.17) |
|||
|
|
|
|
|
|
|
|
|||||||
к |
||||||||||||||
|
|
|
|
|
2 p |
|
||||||||
Для составления уравнения модели StV2 – (H N2) в качестве входной величины удобнее принять напряжение, тогда её передаточную функцию можно записать в виде
WM |
p |
|
к |
|
|
т |
|
2 p |
. |
(3.18) |
|||
|
|
|
|
|
|
|
|||||||
|
|
||||||||||||
|
|
|
p 1 |
|
|||||||||
В операторной форме уравнение примет вид
2 p K p к |
т . |
(3.19) |
Произведя подстановку оператора Лапласа, получим уравнение в дифференциальной форме:
2 |
d |
|
d |
( |
к |
т ), |
(3.20) |
dt |
|
||||||
|
|
dt |
|
|
|
||
где 2 вязкость смеси, Па с; время релаксации, с; t текущее время, с.
Для пояснения физического смысла уравнения (3.20) перепишем его в виде
к |
2 |
d |
|
d |
|
т . |
(3.21) |
dt |
|
||||||
|
|
|
dt |
|
|
||
Согласно полученному уравнению контактные давления, приложенные к поверхности уплотняемого слоя, расходуются на преодоление сил упруговязкого сопротивления и структурного сопротивленияm. Упруговязкая составляющая непрерывно релаксирует с начала приложения нагрузки за счёт перемещения упругого элемента Гука.
Релаксация напряжений d здесь определяется скоростью dt
приложения давления.
При t напряжения релаксируют до остаточного нерелаксирующего напряжения m (рис. 3.6). Под действием давления оба блока включаются в работу и происходит его разделение на составляющие в левом (I) кI и правом (II) кII блоках. Причём в любой момент времени соблюдается равенство
48

(3.22)
Элемент Сен-Венана StV2 начинает деформироваться со скоростью перемещения вязкого элемента H2. Одновременно с этим происходит релаксация напряжений в элементе Максвелла, и напряжения в блоках I и II будут изменяться. В блоке I оноувеличится, а в блоке II на эту же величину уменьшится, т.е. с течением времени происходит перераспределение напряжений между жидкообразной (асфальтовяжущее) и твёрдообразной фазами (минеральный каркас).
В дальнейшем за счёт перераспределения напряжений между блоками модели произойдёт увеличение кI , что вызовет дополнительный сдвиг в элементе жёсткого трения. Такой процесс будет
продолжаться |
до |
установле- |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ния равенства TПРу |
кI к . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
По мере |
роста |
плотности |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
образование |
остаточных |
де- |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
формаций уменьшается, эле- |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
мент StV2 замыкается, т.к. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
величина |
предела |
текучести |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
выше контактных |
давлений, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
развиваемых |
катком: к т. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
В этот период в уплотняемой |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
среде преобладают вязкоупру- |
Рис. 3.6. Кривая релаксации упруговязко- |
||||||||||||||||||
гие деформации, описываемые |
|
|
|
пластичного тела |
|
||||||||||||||
уравнением [108] |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
d |
|
к |
|
|
d |
|
1 |
d |
|
|
|
||||
|
|
|
|
|
|
|
E 1 |
|
|
, |
(3.23) |
||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||
|
|
|
|
dt |
|
1 |
dt |
|
2 |
|
dt |
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||||
где 1, 2 |
– вязкости смеси, Па с, при этом 1 |
2 |
|
1 |
. |
|
|||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||
Согласно этому уравнению возможно неограниченное накоплениевязкихдеформацийпри t , однаков действительностиэтого не произойдёт по нескольким причинам. Во-первых, к тому времени, когдапределтекучести сравняется сконтактными давлениями ( т к), слой покрытия уже имеет определённую плотность и сложившуюся структуру, необратимые деформации, которые могут реализоваться без нарушения сплошности покрытия, уменьшились, и скорость деформаций значительно понижается. Во-вторых, в процессе уплотнения неуклонно уменьшается температура, вязкость смеси существенно увеличивается, прослойки асфальтовяжущего между
49
частицами минерального заполнителя становятся твёрдыми и величина возможных деформаций практически исчерпывается, 0. В-третьих, время взаимодействия вальца катка с уплотняемым слоем составляет 0,05–0,2 с, и за это время значительные вязкоупругие деформации не успевают развиться.
При разгрузке материала закон восстановления деформаций также определяется уравнением (3.23).
3.3. Математическая модель процесса уплотнения асфальтобетонной смеси вибрационным катком
В работе [45] автором предложена математическая модель уплотнения, объединяющая реологические свойства уплотняемого материалаиколебательную систему «пригруз –вибрационныйвалец– асфальтобетонная смесь» (рис. 3.7).
Для более детального изучения принципа работы полученной модели условно разделим ее на две части: одна отражает динамику колебаний вибрационного вальца (рис. 3.8), другая – реологические свойства уплотняемой среды (рис. 3.9).
Дифференциальные уравнения данной колебательной системы (см. рис. 3.8) можно записать в виде системы
|
|
|
|
) с( x1 |
x2 |
) m1g; |
(3.24) |
m1x1 |
b( x1 |
x2 |
|||||
|
|
|
|
) с( x1 |
x2 |
) Q sin t m2 g P(t ), |
(3.24) |
m2 x2 |
b( x1 |
x2 |
|
||||
где m2 – масса вальца, которому сообщаются гармонические колебания от вибровозбудителя, кг; m1 – масса пригруза (масса рамы вальца, приходящаяся на вибрирующий валец), кг; x1 – вертикальное перемещение корпуса катка, возникающее от вращения дебалансного вала вальца и передающееся через резиновые амортизаторы, м; x2 – вертикальное перемещение вибровальца, м; b – коэффициент вязкого трения резиновых амортизаторов, Па∙с/м; с – жесткость резиновых амортизаторов, Н/м;Q– вынуждающая сила вибровозбудителя, Н; – угловая частота вращения вала вибровозбудителя, рад/с; t – время колебания, с; P(t) – реакция на валец со стороны уплотняемой смеси, Н.
Сложив эти два уравнения, получим
|
|
m1g m2g Q sin t P(t ), |
(3.25) |
||
m1x1 |
m2x2 |
||||
откуда |
|
|
|
m1g m2g. |
|
|
|
|
|
(3.26) |
|
P(t ) Q sin t m1x1 |
m2x2 |
||||
50
Так как равенство (3.6) соблюдается на протяжении всего процесса уплотнения, контактное давление вальца на смесь можно определить по формуле
к (t ) |
P(t ) |
, |
(3.27) |
|
|||
|
Fk (t ) |
|
|
где F (t) – площадь пятна контакта вальца со смесью, м2 . |
|
||
k |
|
||
Площадь пятна контакта определяется по формуле |
|
||
Fk (t) Lab (t)B, |
(3.28) |
||
где Lab (t) – длина дуги контакта вальца со смесью, м; B – ширина вальца, м.
По рекомендациям В.А. Баумана и И.И. Быховского [8], при проектировании вибрационных катков коэффициент передачи колебаний от рабочего органа к раме принимают в пределах 1,5 – 4 %.
Поэтому в расчете примем x1 0,02 x2 , |
тогда контактное давление в |
|||||||||
любой момент времени можно определить по формуле |
||||||||||
к |
(t) |
(m1 m2 |
) g |
|
|
Q |
|
sin t |
||
|
|
Lab(t) B |
||||||||
|
|
|
Lab(t) B |
|
|
|||||
|
(0,02 m m ) |
|
|
d2 |
|
|
||||
|
|
1 2 |
h |
(t) |
|
, |
(3.29) |
|||
|
L (t) B |
dt2 |
||||||||
|
|
сл |
|
|
|
|||||
|
|
ab |
|
|
|
|
|
|
|
|
где – относительная деформация уплотняемой смеси; hсл(t ) – толщина слоя смеси, м.
Реологическая модель вибрационного уплотнения смеси (см. рис. 3.9) состоит из трёх параллельно соединённых ветвей (блоков). При этом в любой момент времени соблюдаются условия
(t) 1(t) 2(t) 3(t); |
(3.30) |
к (t ) 1(t ) 2(t ) 3(t ). |
(3.31) |
Так как основание достаточно хорошо уплотнено, жесткость элемента H4 будет намного больше жесткости асфальтобетонной смеси, и в этом случае элемент Н4 в работу не включается.
51

Рис. 3.7. Модель уплотнения асфальтобетонной смеси вибрационным катком
Рис. 3.8. Модель колебательной системы «пригруз – вибрационный валец – асфальтобетонная смесь»
52
Результаты исследований [42] показывают, что для эффективного уплотнения асфальтобетонных смесей необходимо, чтобы возникающие подрабочим органомконтактные давления к были не меньше их предела текучести т, но не больше предела прочности пр, т.е.т(t) к(t) пр(t). Если к(t) т(t), то процесс уплотнения происходит нерезультативно, т.к. в этом случае под действием уплотняющих средств в смесях медленно накапливаются остаточные деформации
[42].
При к(t) пр(t) процесс уплотнения переходит в процесс
разуплотнения, когда превыша- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ется в смеси запас деформа- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
тивной способности и она раз- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
рушается |
на отдельные |
части |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
[42]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При |
приложении |
напря- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
жений больше предела текуче- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
сти деформируются элементы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
StV1 – (H2||N2) – (H3||N3), модель |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
деформируется в режиме уста- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
новившегося течения. Скорость |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
течения определяется вязкостью |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
смеси. Вязкий элемент N1 |
при |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
этом не работает, так как |
де- |
Рис. 3.9. Реологическая модель |
|||||||||||||||||||||
формируется элемент StV1. |
|||||||||||||||||||||||
уплотнения асфальтобетонной смеси: |
|||||||||||||||||||||||
Элемент StV1 в блоке I(1) ото- |
N – модель Ньютона; – вязкость |
||||||||||||||||||||||
бражает |
упруговязкопластич- |
модели Ньютона; H – модель Гука; |
|||||||||||||||||||||
ную деформацию,а блоки II(2)и |
E – модуль упругости модели Гука; |
||||||||||||||||||||||
III(3) – релаксацию напряжений |
|
StV – модель Сен-Венана; |
|||||||||||||||||||||
в смеси. В данном случае во |
Ту – предел текучести модели |
||||||||||||||||||||||
внимание берутся два времени |
|
|
|
|
|
|
|
Сен-Венана |
|||||||||||||||
релаксации напряжений – «бы-
строе» в блоке II(2) и «медленное» в блоке III(3).
«Быстрая» релаксация внутренних напряжений осуществляется за счет взаимного перемещения крупных минеральных зерен, имеющих относительно толстые и малопрочные битумные пленки, что в большей мере проявляется на начальном этапе уплотнения, когда смесь менее плотная. «Медленная» релаксация напряжений проходит за счет релаксационных процессов в растворной части смеси (битум, песок, минеральный порошок). Таким образом, в процессе уплотнения
53

непрерывно происходит перераспределение между двумя составляющими релаксации напряжений [42].
Изменение напряженно-деформированного состояния смеси во время разгрузки описывается набором элементов с формулой N1–(H2||N2)–(H3||N3). Деформация восстанавливается за счет обратимой составляющей полной деформации. Скорость восстановления определяется вязкостью упругого последействия. Одновременно с восстановлением деформаций происходит релаксация напряжений в блоках II(2) и III(3).
Для составления дифференциального уравнения состояния модели при напряжении больше предела текучести удобно пользоваться методом передаточных функций.
Принимая за входную величину деформацию, передаточная функция блока I(1) будет иметь вид
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
W( p) |
|
|
|
т |
. |
|
|
|
|
|
|
|
|
|
|
|
|
(3.32) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Принимая за входную величину контактное давление, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
передаточные функции блоков II(2) и III(3) будут иметь вид |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
W( p) |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
2p E2 |
; |
|
|
(3.33) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
2 |
|
|
к |
|
|
|
|
|
|
E2 |
|
|
|
2p |
|
|
|
|
|
E2 2p |
|
|
|
|||||||||||||||||||||||||||
|
|
W( p) |
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
3p E3 |
. |
|
|
(3.34) |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
к |
|
|
|
|
E |
|
|
|
|
|
|
|
p |
|
|
|
|
|
E p |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 3 |
|
|
|
|
|
|
|
||||||||||||||||||
Общая передаточная функция примет вид |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
E |
p |
|
|
|
|
E p |
|
|
|
||||||||||||||||||
|
W( p) |
к |
|
т |
|
|
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|
3 3 |
|
; |
(3.35) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
p E |
|
p E |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
3 |
|
|
||||||||||
|
|
E |
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
E p |
|
|
|
|
|
|
|
K |
|
y |
|
|
|
|||||||||||||||||||||||
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
, |
|
(3.36) |
||||||||||||||
|
|
E ( |
2 |
p 1) |
|
E ( p 1) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
где 2 |
и 3 – время |
|
релаксации |
|
в |
|
блоке II(2) |
и блоке |
III(3) |
||||||||||||||||||||||||||||||||||||||||||||
соответственно, с; 2 и 3 – вязкость смеси в блоке II(2) и блоке III (3) соответственно, Па∙с; Е2 и Е3 – модули деформации смеси в блоке
II(2) и блоке III(3) соответственно, Па.
|
d2 |
|
|
|
d2 |
|
|
d |
|
d |
|
|||||||
dt2 |
|
dt2 |
|
dt |
||||||||||||||
2 3 |
|
3 2 |
|
2 dt |
3 |
2 3 |
||||||||||||
|
|
|
d 2 |
|
|
d 3 |
|
|
|
y |
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
|
к т . |
|
|
|||||
|
dt |
dt |
|
|
||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
||||||||
d2 2 3 dt2
(3.37)
54
Ввиду того, что распределение контактного давления вальца на смесь между тремя блоками в процессе уплотнения представляет определенную трудность, зададимся соотношениями
2(t) n к(t); |
(3.38) |
3(t) m к(t ). |
(3.39) |
Коэффициенты n и m будут постоянно изменяться в процессе уплотнения.
Тогда дифференциальное уравнение реологической модели перепишется в виде
( |
|
) |
d2 |
( |
2 |
|
3 |
) |
d |
|
(nm ) |
d2 K |
( |
2 |
n |
||||||
dt2 |
dt |
dt2 |
|||||||||||||||||||
2 3 |
|
3 2 |
|
|
|
|
|
2 3 |
|
|
|
||||||||||
|
|
|
|
d к |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|||
|
3 |
m ) |
|
|
|
к т |
. |
|
|
|
|
|
|
|
|
(3.40) |
|||||
dt |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Таким образом, имеем систему двух дифференциальных уравнений, описывающую гармонические колебания вальца и реологические свойства асфальтобетонной смеси:
|
|
|
|
|
|
(m m |
2 |
) g |
|
|
Q |
|
|
|
|
(0,02 m m |
2 |
) |
|
|
|
|
d |
2 |
|
|
|||||||||||||||||
|
k |
(t ) |
|
1 |
|
|
|
|
|
|
|
|
sin t |
|
|
1 |
|
|
h |
|
(t ) |
|
|
; |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
(t ) B |
|
|
|
|
|
2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
L (t ) B |
L (t ) B |
|
|
|
|
|
|
сл |
|
dt |
|
|||||||||||||||||||||||||
|
|
|
|
|
d2 |
|
|
ab |
|
|
|
d2 |
|
ab |
|
|
|
d |
|
|
ab |
|
d2 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n m) |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
dt2 |
|
|
|
dt2 |
2 dt |
3 |
dt |
|
dt2 |
|
|
|
|
||||||||||||||||||||||||||||
|
2 3 |
|
|
|
|
3 2 |
|
|
|
|
|
|
2 3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
d K |
|
|
|
|
|
|
d K |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
(3.41) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
2 |
n |
|
|
|
|
|
|
|
3 |
m |
|
|
|
|
|
к т . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
dt |
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обозначив начальные условия, получим решение системы |
|
||||||||||||||||||||||||||||||||||||||||||
методом сеток. Вывод и полное решение системы представлены в |
|
||||||||||||||||||||||||||||||||||||||||||
работе [45]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Вычисляются |
все значения |
i |
и |
i для |
каждого |
момента |
|
||||||||||||||||||||||||||||||||||||
времени, при этом после каждого цикла необходимо проверять |
|
||||||||||||||||||||||||||||||||||||||||||
условие i |
iT ( i |
– |
контактное давление вальца на i-м шаге; iT |
|
– |
|
|||||||||||||||||||||||||||||||||||||
предел текучести асфальтобетонной смеси на i-м шаге расчета). Расчет |
|
||||||||||||||||||||||||||||||||||||||||||
прекращается на (i 1) |
|
-м шаге при условии i |
iT , т.к. дальнейшее |
|
|||||||||||||||||||||||||||||||||||||||
уплотнение неэффективно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
55
i (t) |
i (t) |
|
|
ki |
ki 1 h |
|
|
h e |
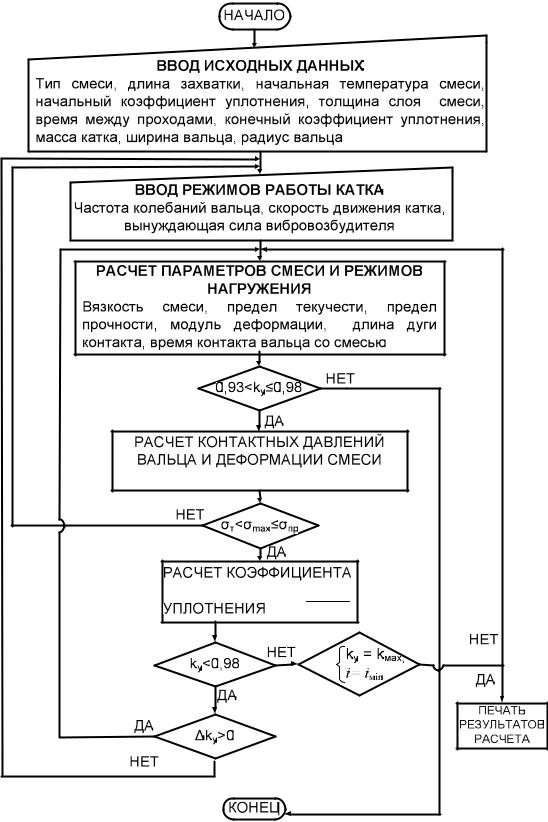
Рис. 3.10. Алгоритм расчета рациональных параметров вибрационных катков
56
