2488

х t A KC х t B KD u t Ky t ;

у t Cх t Du t ; r t Q y t у t ,

где r t Rp – остаточный вектор; xˆ, yˆ – оценки векторов состояния и выходного сигнала соответственно; матрица Q Rp m – матрица весов остатков.

Системное уравнение для вектора ошибки оценивания состояния e t x t xˆ t и вектора остатка r t :

е t (A KC)e t Ed t R1 f t KR2 f t ;

r t QCe t QR2 f t .

Преобразование Лапласа отклика остатка на неисправности и возмущения:

r s QR2 f s QC sI A KC 1 R1 KR2 f sQC sI A KC 1E d s e 0 ,

где e 0 – начальное значение ошибки оценивания состояния. Очевидно, что остаток r t и ошибка оценивания e t ненулевые

даже при отсутствии неисправностей. Трудно отличить влияние неисправностей от влияния возмущений, действующих на систему. Влияние возмущений приводит к ложным срабатываниям FDI, поэтому для минимизации ложных срабатываний необходимо формировать остатки, декомпозированные относительно возмущений и неисправностей.

Многокритериальная диагностика неисправностей. И неис-

правности и возмущения действуют на остаток, трудно различить эти два эффекта. Необходимо увеличить влияние неисправностей на остаток и уменьшить влияние возмущений. Увеличить влияние неисправностей можно максимизацией следующего индекса в заданном диапазоне частот:

1, 2

где , обозначают минимальные и максимальные сингулярные зна-

чения матрицы соответственно.

171

Влияние возмущений и начальных условий можно редуцировать

Кроме неисправностей и возмущений на остаток влияет шум. Пусть t шум входного сигнала; t шум чувствительного элемента; системные уравнения в этом случае

x t Ax t Bu t R1 f t t ;

y t Cx t Du t R2 f t t .

Шум чувствительного элемента, так же как неисправности, действуя через R2 f t , действует на остаток таким же образом, но диапазоны частот неисправностей и шума различны. Для редуцирования влияния шума на остаток необходимо минимизировать норму

Q QC j I A KC 1K .

Влияния возмущений и неисправностей могут быть разделены при использовании различных частотно-зависимых весовых штрафов:

1, 2

Для максимизации влияния неисправностей на низких частотах и минимизации шумов на высоких вводится частотно-зависимый весовой множитель W1 j , имеющий большое значение амплитуды на низких частотах и малое значение на высоких. Частотный эффект W3 j должен быть обратным: W3 j W1 1 j .

Рассмотрим установившееся значение остатка: r QR2 f QC A KC 1 KR2 R1 f A KC 1d . По-

сле времени переходного процесса стационарное значение остатка играет важную роль в FDI. Идеально это должно реконструировать сигнал неисправности. Влияние возмущения на остаток может быть

редуцировано минимизацией индекса: 4 K A KC 1 ; при этом

матрица K увеличивается и норма A KC 1K приближается к по-

стоянному значению. Это означает, что влияние неисправности на ос-

172

таток не изменяется уменьшением влияния возмущения, что и требуется для хороших характеристик FDI.

Распределение возмущений и локализация неисправности.

Предположим, что матрица распределения возмущений известна: d t Ed' t , где E известная матрица; d' t неизвестный вектор. В

Для локализации неисправности должно быть сформировано структурированное остаточное множество. Структурированный означает чувствительность к одним неисправностям и нечувствительность к другим. Неисправности могут быть разделены на две группы: f1 t , f2 t уравнение системы в этом случае запишется

x t Ax t Bu t R11 f1 t R12 f 2 t d t ; y t Cx t Du t R21 f1 t R22 f 2 t .

Если проектировать остаток, чувствительный к f1 t и нечувствительный к f2 t , то индекс 1 K,Q должен быть изменен:

1, 2

Многокритериальная диагностика неисправностей. В общем случае не существует решения, которое минимизирует все индексы характеристик. Параметр, обеспечивающий минимизацию частного индекса, может привести к недопустимому росту других индексов характеристик, следовательно, проектирование должно проводиться с компромиссами. Подходом к решению многокритериальной задачи оптимизации при проектировании СУ является метод неравенств в комбинации с Gas, основная концепция которого в замене минимизации индексов ограничениями в форме неравенств на индексы характеристик. То есть многокритериальная оптимизация переформулируется как задача нахождения множества параметров Z,W,Q, удовлетворяющих следующим неравенствам: i Z,W,Q i, i 1,...,5, где действительные числа i представляют численные границы (требования разработчика) индексов характеристик i Z,W,Q .

173

Если минимальное значение i Z,W,Q , достигаемое минимиза-

цией, есть i*, то границы критериев должны удовлетворять неравен-

ству i i*, так как множество параметров минимизирующих частные индексы характеристик могут увеличивать другие индексы. Если

Задача многокритериальной оптимизации – найти множество параметров для размещения всех индексов характеристик в приемлемых областях. Регулируя границы i , можно акцентировать любую из це-

лей. Если индекс j важен для задачи, можно приблизить j к *j .

Пусть i множество параметров Z,W,Q , для которых выполняется i-й критерий: i Z,W,Q : i Z,W,Q i . Тогда допустимое

может быть найдено методом неравенств в сочетании с GAs.

3.5. Нахождение равновесия Нэша динамических игр n лиц

Игра n лиц определена множеством Sk ; k 1,...,n допустимых стратегий каждого игрока k и платежными функциями fk . Предполагается, что игроки могут выбрать свои стратегии независимо друг от друга. Однако в некоторых приложениях общая сумма ресурсов, используемых всеми игроками, ограничена. Будем использовать стратегическое представление игры n лиц в виде

174

p s xk p' s Ck' Lk 0,

получим p' s xk' s p' s xk s p" s Ck" xk s xk' s 0, считая, что

xk' s p' s xk s p" s 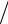p' s Ck" xk s 0. Равновесие Нэша –

единственное решение s* монотонного уравнения с одним неизвест-

n

ным: xk s s 0, где s* полный выпуск продукции в точке рав-

k 1

новесия и равновесный выпуск продукции фирмы k: xk* xk s* .

175

Вычисление равновесия Нэша. Существует несколько различных концепций вычисления равновесия Нэша. Рассмотрим три наиболее часто используемых метода: решение для фиксированных точек, редуцирование к вариационным неравенствам и преобразование задачи о равновесии к задаче оптимизации.

Пусть g лучшее отображение реакции x g x g1 x ... gn x ,

тогда x* равновесие Нэша, если и только если x* g x* . Если g x

функция одной переменной, то x* фиксированная точка, если и только если x* g x* ; в этом случае необходимо решить систему алгебраических уравнений. Если g x множество, то существует система неравенств, независимых от x, необходимо найти допустимое решение этих неравенств.

Hr x* ,x* Hr x* ,y ; x S, то max h x,r T x x* 0, где h: S RM:

дующий итеративный алгоритм: пусть задан произвольный x 1 S ;

ность итерационной последовательности x 1 ,x 2 ,..., которая сходится к единственному равновесию Нэша.

Распространение на динамические системы. Рассмотрим ди-

намическую игру олигополии одного продукта. Маржинальная при-

нальная прибыль положительна (отрицательна), то фирма увеличивает (уменьшает) выпуск своей продукции; если маржинальная прибыль

176

равна нулю, то (учитывая вогнутость fk в xk ) выпуск максимизирует прибыль. Корректирующая концепция может моделироваться следующим образом:

xk t Kk p i xi xk p' i xi Ck' xk ;Kk 0; k 1,...,n.

Динамическое равновесие этой системы имеет точку внутреннего равновесия. При исследовании динамических игр рассмотрим только асимптотическое поведение траектории t . Локальная асимптотическая устойчивость исследуется на основе локальных собственных значений якобиана. Якобиан имеет структуру J D a 1T , где

Это уравнение эквивалентно полиномиальному уравнению степени n. Найдем n действительных отрицательных корней, следовательно, динамическое равновесие локально асимптотически устойчиво.

3.6. Исследование СУ с помощью дифференциальных игр

Рассмотрим задачу дифференциальных игр – в нашем случае обобщенную задачу оптимального управления с двумя игроками.

Один игрок выбирает управление u t u Rmu и минимизирует свой функционал качества, другой игрок выбирает управление v t v Rmυ и максимизирует свой функционал качества. Дифференциальная игра называется игрой с нулевой суммой, если два функционала качества идентичны. Дифференциальные игры интересны в связи H теорией робастного управления.

177

Применение теории оптимального управления к теории дифференциальных игр является прямым: в принципе максимума Понтрягина функция Гамильтона минимизируется по отношению к управлению u; в принцип минимакса Нэша-Понтрягина функция Гамильтона одновременно минимизируется по отношению к u и максимизируется по отношению к v.

Будем рассматривать системы, инвариантные во времени, с неограниченными управлениями u, v и свободным (незакрепленным) состоянием в финальное время tb .

Общая постановка задачи. Найти такие непрерывные управления u: ta,tb Rmu ; v: ta,tb Rmv , что система x t f x t ,u t ,v t переводится из начального состояния x ta xa в терминальное с временем

tb

tb с функционалом качества J u,v K x tb (x x t ,u t ,v t dt, ми-

ta

нимизируемым по отношению к u и максимизируемым по отношению к v.

Подзадача 1. Оба игрока используют разомкнутое управление: u t u t,xa,ta ;v t v t,xa,ta .

Подзадача 2. Оба игрока используют замкнутое управление: u t ku x t ,t ;v t kv x t ,t .

Специальная постановка задачи с разделением переменных.

Функции f и L могут быть разделены:

f x t ,u t ,v t =f1 x t ,u t +f2 x t ,v t ;L x t ,u t ,v t =L1 x t ,u t +L2 x t ,v t .

Принцип минимакса Нэша-Понтрягина. Функция Гамильтона

H :Rn Rmu Rmv Rn R.

H x t ,u t ,v t , t L x t ,u t ,v t T t f x t ,u t ,v t .

ния, то выполняются следующие условия:

o tb = xK xo tb ;

178

б) гамильтониан H xo t ,u t ,v t , o t имеет седловую точку по отношению к u Rmu ; v Rmv ; t ta, tb .

H xo t ,uo t ,vo t , o t H xo t ,u t ,vo t , o t ; u Rmu ; H xo t ,uo t ,vo t , o t H xo t ,uo t ,v t , o t ; v Rmv ;

в) далее в случае подзадачи 2 при применении закона управления v t kv x t , t , uo минимизирующее управление задачи оптимального управления; при применении закона управления u t ku x t , t , vo максимизирующее управление задачи оптимального управления.

Теория Hamilton-Jacobi-Isaacs (HJI). В принципе минимакса Нэ-

ша-Понтрягина выражено необходимое условие для H для получения равновесия Нэша в седловой точке uo, vo формированием нера-

венств H xo,uo,v, o H xo,uo,vo, o H xo,u,vo, o .

Для распространения теории HJI на теорию дифференциальных игр сформулируем необходимое условие равновесия Нэша в виде minmaxH xo,u,v, o maxminH xo,u,v, o H xo,uo,vo, o .

x t f x t ,u t ,v t развивается от начального состояния x ta xa к конечному со временем tb и функционалом качества:

tb

J u,v K x tb L x t ,u t ,v t dt,

ta

минимизируемая управлением u и максимизируемая v.

Предположим, что функция Гамильтона H L x,u,v T f x,u,v

имеет единственное равновесие Нэша для x, Rn . Соответствую-

щие H-минимизиующие и H-максимизирующие управления: u~ x, ,

~v x, .

179

состояния x ta xa в состояние с финальным временем tb и функционал качества

мые условия, следующие из принципа минимакса Нэша-Понтрягина: xo= H=Axo+B1uo+B2vo;

o= xH= Qxo AT o;

uH=0=uo+B1T o;

vH=0= 2vo+B2T o .

Таким образом, минимаксная функция Гамильтона определяет H-минимизирующие и H-максимизирующие законы управления: uo t B1T o t ;vo t 2B2T o t . Подстановка их в дифференциальное уравнение для x приведет к линейной двухточечной граничной задаче: xo t =Axo t B1 B1T o t + 2B2B2T o t ; o t = Qxo t AT o t ; xo ta =xa; o tb =Fxo tb .

Два дифференциальных уравнения однородны в xo, o и в ко-

нечное время tb вектор o tb линейная функция вектора xo tb ; поэтому примем o t K t xo t , где K t n n матрица.

Дифференцированием найдем

uo t B1T K t xo t ;vo t 2B2T K t xo t , где симметричная положи- тельно-определенная n n матрица K t решение дифференциального

180