
- •ВВЕДЕНИЕ
- •1. РАСЧЕТ КАК ИНСТРУМЕНТ ОБЕСПЕЧЕНИЯ НАДЕЖНОСТИ КОНСТРУКЦИЙ
- •1.1. Изменчивость расчётных параметров
- •1.2. Применение теории вероятностей для учета изменчивости
- •1.3. Особенности нормального закона распределения
- •1.4. Параметры метода расчёта по допускаемым напряжениям
- •1.6. Вероятностная зависимость параметров исходных данных
- •1.7. Метод расчёта по разрушающим нагрузкам и условный коэффициент запаса
- •1.8. Расчётные параметры метода предельных состояний
- •1.9. Совершенствование метода предельных состояний
- •1.10. Учёт фактора времени
- •2.3. Постоянные нагрузки
- •2.4. Полезные нагрузки на перекрытия
- •2.5. Снеговые нагрузки
- •2.6. Ветровые нагрузки
- •2.7. Температурные климатические воздействия
- •2.8. Крановые нагрузки
- •2.9. Аварийные ударные воздействия
- •2.11. Сочетания нагрузок
- •3. ИЗМЕНЧИВОСТЬ СВОЙСТВ СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ
- •3.1. Основные положения
- •3.2. Строительные стали
- •3.3. Бетоны
- •3.4. Строительные растворы
- •3.5. Кирпич и каменная кладка
- •3.6. Древесина
- •3.7. Грунты
- •4. ЗАДАЧИ РАСЧЁТА КОНСТРУКЦИЙ НА НАДЁЖНОСТЬ
- •4.1. О надёжности ограждающих конструкций при расчёте на теплопередачу
- •4.2. Вероятностная оценка прочности железобетонных элементов по нормальным сечениям при изгибе
- •4.3. Изменчивость несущей способности изгибаемой конструкции
- •4.4. Неопределенность расчетных моделей конструкций
- •Библиографический список
1.9. Совершенствование метода предельных состояний
Представим граничное условие области предельных состояний конструкций в виде
S = R −Q > 0. |
(1.75) |
~ |
|
Если принять, что вероятность выполнения неравенства (1.75) есть вероятность сохранности конструкции, то вероятность отказа (разрушения) определяется выражением
PQ = |
0 |
|
∫ p(S)dS . |
(1.76) |
|
Н.С. Стрелецкий вместо |
−∞ |
разрушения исследовал |
вероятности |
другую меру безопасности конструкций − гарантию неразрушимости
[62]:
|
R |
|
Г = 1 − ω1ω2, |
(1.77) |
|
|
|
|
А |
|
|
где ω1 |
= ∫ p(R)dR |
|
|
|
|
− вероятность реализацииИзначения прочности ни |
|||||
|
−∞ |
|
|
|
|
же расчётного; ω2 |
∞ |
б |
|
||
|
|
||||
= ∫ p(Q)dQ − вероятностьДреализации значения на- |
|||||
|
|
Q |
|
|
|
|
|
и |
|
|
|
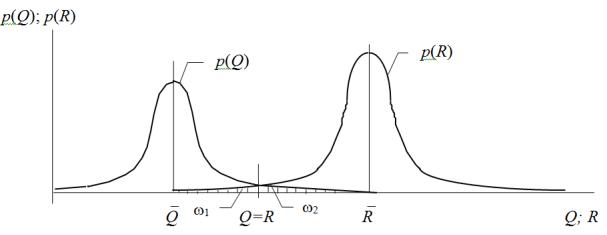
грузки выше расчётного (рис. 1.8). |
|
||||
|
С |
|
|
|
|
Рис. 1.8. Показатели безопасности по методу Н.С. Стрелецкого
Гарантия неразрушимости завышает вероятность безотказной
работы конструкции, так как произведение ω1ω2 соответствует вероятности одновременного появления этих двух событий, а вероятность
40
отказа из-за реализации одного события исключается. Чтобы уточнить оценку, впоследствии для некоторых случаев был установлен
верхний предел вероятности отказа ω1ω2 < ω1 + ω2 − ω1ω2 [15]. В настоящее время эту модель иногда применяют для решения практических задач [39, 57].
С целью совершенствования метода расчёта конструкций по предельным состояниям представим условие надёжности в виде сис-
темы двух событий R~ ≥ U и Q ≤ U, где U –детерминированное значение предельного состояния, соответствующее равенству R~ = Q
[36].
Выполним логический анализ этой системы. В общем случае R~ и Q являются элементами не только бесконечного множества S, но и
подмножеств R SR и |
|
И |
Q SQ (R содержится в SR, Q содержится в |
||
~ |
|
|
SQ). Важным свойством такого множества является пересечение (ло- |
||
|
Д |
|
гическое произведение) Q ∩ R или QR. |
|
|
В вероятностных моделях логическое произведение характери- |
||
зуется совмещением (совместным осуществлением) двух случайных |
||
|
А |
|
событий, которые назовём безотказностями и обозначим как |
(1.78) |
|
BR = R ≥U и BQ = Q ≤U . |
||
~ |
|
|
б |
|
|
Вероятность каждого из этих событий характеризуется обеспе- |
||
ченностями расчётных значений U несущей способности и нагрузоч- |
||
ного эффекта, которые в о щем случае не равны и выражаются вероятностями Р(ВR) и Р(BQ), которые Б.И. Снарскис назвал «дальностями
|
~ |
AQ = Q >U , противоположные обес- |
отказа». События AR = R <U |
||
печенностям расчётныхизначений, будем, как и прежде, называть от- |
||
казами, вероятности которых |
равны Р(АR) = 1 – Р(ВR) и |
|
Р(АQ) = 1 – Р(BQ). |
|
|
С |
|
|
В теории вероятностей используется принцип целесообразности |
||
применения противоположных событий, согласно которому при умножении вероятностей следует отдавать предпочтение операциям с событиями, распадающимися на меньшее число вариантов, т.е. с менее вероятными событиями – отказами. Поэтому для дальнейшего анализа рассмотрим совмещение неблагоприятных событий (отказов), учитывая, что теория вероятностей оперирует также понятием условной вероятности какого-либо события А, которая вычисляется в предположении наступления другого события В и обозначается как равен-
ство Р(А/В) = Р(В/А).
41
Совмещаемые события-отказы АR и АQ независимы по вероятности, так как, например, появление события АQ с вероятностью Р(АQ) > 0 (превышение предельного значения нагрузки) не изменяет вероятности (обеспеченности) события АR (занижение прочностных свойств конструкции). При этом Р(АR/АQ) = Р(АR) при условии Р(АQ) > 0. Предпосылка независимости событий распространяется, прежде всего, на практические случаи статического загружения конструкций. Возможны частные случаи проявления вероятностной зависимости внешних воздействий и свойств конструкции, требующие специальных исследований взаимодействия.
Вероятность совмещения (совместного появления) независимых, логически связанных событий AQ ∩ AR определяется по правилу
сочетаний теории вероятности
Надёжность конструкции или вероятностьИбезотказности системы определяется зависимостью, вытекающей из классических теорем
P(AQ ∩ AR )= P(AR )P(AQ ). |
(1.79) |
Полученное выражение характеризует отказ системы АS с веро-
ятностью Р(АS) = Р(R̃< Q̃).
теории надёжности |
|
)=1− P(A )=1Д− P(A )P(A ). |
|
||
P(B |
S |
(1.80) |
|||
|
S |
R |
Q |
|
|
Полученное выражение идентично гарантии неразрушимости – |
|||||
параметру надёжности, предложенномуА |
Н.С. Стрелецким. Метод |
||||
Н.С. Стрелецкого, по мнен ю А.Р. Ржаницына, имеет существенный |
|||||
недостаток, выражающ йсябв том, что при детерминированных зна- |
|||||
чениях нагрузкиСилиипрочности вероятность отказа сооружения нулевая и получается Р(ВS) = 1 [55]. Однако этот случай противоречит условию, в котором оба параметра являются случайными, кроме этого, в теории вероятностей варианты Р(АR) = 0 или Р(АQ) = 0 исключаются, так как ведут к неопределённости. Чтобы выйти из этой неопределённости, достаточно перейти к операциям с противоположными событиями. Очевидно, это надо иметь в виду при применении и анализе выражения (1.80).
Графическая интерпретация выражения (1.80) представлена на рис. 1.9, на котором совмещена «числовая плоскость» на осях случай-
ных величин R~ и Q , распределённых по функциям f(R) и f(Q), и плоскость системы вероятностных координат Р(R) – Р(Q).
42

Рис. 1.9. Зависимость Р(АS) =И1 – Р(ВS)
Единичная площадь квадрата в осях вероятностей состоит из двух основных участков: заштрихованногоДучастка отказов с площа-
дью, эквивалентной вероятности отказа системы Р(А ) = Р(А )Р(А ) =
А S R Q
=1 – Р(ВS), и соответствующего участка безотказности с площадью Р(ВS), частями которого являются участки условной вероятности
Р(ВQ/АR) = Р(BQ) и Р(ВR/AQб) = Р(ВR).
Точкой пересечения числовых координатных осей является число U, соответствующееипредельным значениям исходных параметров. Вероятностные коорд наты Р(ВR) и Р(ВQ) точки U характеризуют обеспеченностьСрасчётных значений исходных параметров. Если принять, что надёжность характер зуется вероятностью отклонения расчётного параметра от среднего значения, то длина отрезка U – U (U – число, соответствующее средним или нормативным значениям исходных параметров) в вероятностных координатах является характеристикой надёжности системы. Отсюда нетрудно получить выраже-
ние для надёжности конструкций при расчёте по предельному со-
стоянию P(U) 2 = [P(R) – P( R )]2 + [P(Q) – P(Q )]2.
Систему (1.77) можно также представить в виде структурной схемы с параллельным соединением элементов – событий, вероятности отказов которых равны Р(АR) и Р(АQ) (рис. 1.10). Надёжность такой системы также определяется уравнением (1.80).
Выражение (1.80) позволяет не только оценить надёжность (безотказность) конструктивной системы, рассчитанной по методу предельных состояний, но и по заданному значению надёжности решать
43

две группы задач. Во-первых, по предварительно принятым значениям расчётных нагрузок UQ и их обеспеченности Р(BQ) можно определить требуемую обеспеченность Р(ВR) расчётных значений несущей способности конструкции и тем самым принять более эффективное конструктивное решение и, во-вторых, по предварительно принятым значениям расчётных UR и вероятностных характеристиках Р(ВR) несущей способности можно уточнить срок службы конструкции по показателям временных нагрузок и воздействий.
Рис. 1.10. Структурная схема вероятностногоИусловия прочности
Пример 1.8. Проектная надёжность сооружения Р(ВS) = 0,999; обеспеченность расчётного значения U несущей способности Р(ВR) = 0,99865; коэффици-
ент вариации постоянной нагрузкиА, распределённойДпо нормальному закону, vQ = 0,05. Уточнить коэффициентбнадёжности по нагрузке.
Вероятность отказа по несущей способности Р(АR) = 1 – 0,99865 = 0,00135. Из выражения (1.80) определяем вероятность отказа по нагрузке Р(АQ) = (1 – 0,999)/0,00135 = 0,74. О еспеченность расчётного значения U постоянной нагрузки Р(BQ) = 1 – 0,74 = 0,26. По таблицам функции центрированного (относительно среднего значен я нагрузки) нормального распределения нахо-
дим β = 0,707. Коэфф ц ент надёжности по нагрузке в настоящее время опреде- |
||
ляется по формуле γf =и1 + βvQ (считается, что при расчёте по прочности β = 3 и |
||
γf |
= 1,15). |
Уточненный коэффициент надёжности по нагрузке |
γf |
= 1 + 0,707·0,05 |
= 1,035 < 1,15. Нормативное (среднее) значение нагрузки при |
принятых исходныхСданных можно принять в 1,15/1,035 = 1,11 раза больше.
Основные положения метода предельных состояний направлены на обеспечение безотказной работы конструкций с учётом изменчивости свойств материалов, нагрузок, воздействий, геометрических характеристик конструкций, условий работы и степени ответственности проектируемых объектов. Безотказность работы − это способность сохранять заданные эксплуатационные качества конструкции в течение определённого срока службы при любых возможных нагрузках и воздействиях. Это основное свойство, определяющее надёжность не только строительных конструкций, но
44
и зданий, сооружений в целом. При этом степень ответственности определяется материальным и социальным ущербом в результате нарушения работоспособности конструкций. Т.е. расчёт по предельным состояниям имеет целью обеспечить надёжность здания или сооружения в течение всего срока службы и при производстве работ.
Положительным качеством метода предельных состояний является отражение вероятностной природы основных расчётных факторов и возможность учёта их изменчивости. Приоритет в развитии и применении этого метода принадлежит российским специалистам, метод принят на вооружение многими международными организациями и обязателен для применения в разных странах. Определённое усовершенствование он получил в международном стандарте (ИСО) «Общие принципы проверки надёжности конструкцийИ».
не позволяет проектировать их с заданным уровнем надёжности и
Однако в существующем виде детерминированный метод предельных состояний не даёт чёткого ответаДо надёжности конструкций,
оценить качество проектного решения по этому критерию. Схема на-
значения коэффициентов надёжности, принятая в нормах, не вполне
правильно отвечает статистической природе расчётных величин и за-
частую приводит к неэкономичным решениям, в частности, при нали-
чии в расчётной формуле ольшого числа случайных параметров, |
|
и |
|
особенно в отношении нагрузокАи воздействий. Кроме этого, анализ |
|
расчётных моделей показывает, что некоторые расчетные параметры |
|
С |
связь сложная и меняется с |
взаимосвязаны, пр чём стохастическаяб |
|
течением времени. Однако формулы метода предельных состояний не учитывают срок службы конструкций.
В настоящее время существуют две точки зрения. Во-первых, поскольку метод предельных состояний основан на полувероятностном подходе, а теория надёжности значительно продвинулась вперёд, для решения задачи надёжности необходимо перейти к принципиально новой методике проектирования. С другой стороны, такой подход позволяет инженеру-конструктору гарантировать безопасность и эксплуатационную пригодность конструкции с высокой вероятностью и поэтому полувероятностная основа имеет положительный характер, а реальный путь совершенствования метода предельных состояний заключается в уточнении и дифференциации коэффициентов надёжности.
45
