
- •ВВЕДЕНИЕ
- •1. РАСЧЕТ КАК ИНСТРУМЕНТ ОБЕСПЕЧЕНИЯ НАДЕЖНОСТИ КОНСТРУКЦИЙ
- •1.1. Изменчивость расчётных параметров
- •1.2. Применение теории вероятностей для учета изменчивости
- •1.3. Особенности нормального закона распределения
- •1.4. Параметры метода расчёта по допускаемым напряжениям
- •1.6. Вероятностная зависимость параметров исходных данных
- •1.7. Метод расчёта по разрушающим нагрузкам и условный коэффициент запаса
- •1.8. Расчётные параметры метода предельных состояний
- •1.9. Совершенствование метода предельных состояний
- •1.10. Учёт фактора времени
- •2.3. Постоянные нагрузки
- •2.4. Полезные нагрузки на перекрытия
- •2.5. Снеговые нагрузки
- •2.6. Ветровые нагрузки
- •2.7. Температурные климатические воздействия
- •2.8. Крановые нагрузки
- •2.9. Аварийные ударные воздействия
- •2.11. Сочетания нагрузок
- •3. ИЗМЕНЧИВОСТЬ СВОЙСТВ СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ
- •3.1. Основные положения
- •3.2. Строительные стали
- •3.3. Бетоны
- •3.4. Строительные растворы
- •3.5. Кирпич и каменная кладка
- •3.6. Древесина
- •3.7. Грунты
- •4. ЗАДАЧИ РАСЧЁТА КОНСТРУКЦИЙ НА НАДЁЖНОСТЬ
- •4.1. О надёжности ограждающих конструкций при расчёте на теплопередачу
- •4.2. Вероятностная оценка прочности железобетонных элементов по нормальным сечениям при изгибе
- •4.3. Изменчивость несущей способности изгибаемой конструкции
- •4.4. Неопределенность расчетных моделей конструкций
- •Библиографический список

При операции с несколькими случайными величинами, их системами или функциями учитывается не только их функциональная, но и вероятностная или стохастическая зависимость. Считается, что функциональная зависимость является проявлением наиболее тесной вероятностной зависимости [11]. Необходимое и достаточное условие
независимости, например, двух случайных величин x |
и y вытекает |
из теоремы умножения законов распределения |
|
f (x, y)= f1(x)f2 (y). |
(1.7) |
Для описания функций зависимых случайных величин кроме математических ожиданий и дисперсий составляющих необходимо знать одну из характеристик связи, корреляционный момент (кова-
|
Kxy = xy − x y |
И |
риацию) |
или коэффициент линейной корреляции |
|
ρxy = Kxy |
sx sy , абсолютная величина которого не больше единицы. |
|
|
|
Д |
При линейной зависимости ρxy = ±1. В более сложных случаях имеет
место нелинейная и множественная корреляции. Для независимых величин Kxy = 0. Важное свойствоАраспределения суммы независимых
случайных величин: дисперсия суммы равна сумме дисперсий. Теория надёжностибпозволяет достаточно точно учесть случай-
ный характер нагрузок, свойств материалов и геометрических характеристик конструкций.
При расчётеСконструкц й на надёжность приходится иметь дело с непрерывно меняющ м ся параметрами времени, повторения нагрузки и т.д. Тогда вместо случайных величин производятся операции со случайными функциями. Если аргументом случайной функции является время, то функции называют случайным процессом.
1.3. Особенности нормального закона распределения
Нормальный закон распределения (распределение Гаусса), графические особенности которого показаны на рис. 1.3, имеет особое значение в теории надёжности строительных конструкций. Большинство задач может быть решено достаточно просто, если исходные переменные имеют нормальное распределение.
12

Рис. 1.3. Плотность распределения f(x) случайной величины x по нормальному закону и её функция F(x)
Достоинством нормального закона распределенияИ является то
обстоятельство, что линейные комбинации случайных величин, подчиняющихся ему, имеют также нормальныйДзакон распределения. К
этому закону стремится сумма независимых (или слабо зависимых) случайных величин, каждая из которых может быть распределена по любому другому закону. Этим законом часто аппроксимируют изменчивость механических свойств материалов, геометрических размеров конструкций и постоянных нагрузок.
Нормальный закон распределения характеризуется плотностью |
||||||||
вероятности вида |
и |
|
А |
|
|
~ |
||
С |
|
1 |
|
2 |
2 |
|
||
|
f (x) =бexp−(x − x) |
|
2sx , |
(1.8) |
||||
|
|
sx |
|
2π |
|
|
|
|
где sx − среднеквадратическое отклонение случайной величины x от
математического ожидания x ; − ∞ < x < + ∞ − область вероятных зна- |
|||||
чений x . |
|
|
|
|
|
~ |
|
|
|
|
|
Функция распределения или интегральная закономерность рас- |
|||||
пределения при нормальном законе распределения |
|
||||
x |
1 |
|
|
x |
|
F(x) = ∫ f (x)dx = |
|
|
∫exp[−(x − x)2 2sx2 ]dx . |
(1.9) |
|
|
|
|
|||
sx |
|
||||
−∞ |
2π −∞ |
|
|||
Данный интеграл не вычисляется в замкнутом виде. Для приведения его в более удобную форму используют замену переменной x выражением, которое применяется при нормировании расчётных значений параметров и теории надёжности:
13

x = x + usx , |
(1.10) |
где u − нормированное (стандартизированное) значение вероятности
(1.2).
Следует отметить, что заданная любым законом распределения случайная величина с конечными значениями математического ожидания и дисперсии может быть выражена через стандартизированную вероятность u.
Упростим выражение (1.8) и приведем его к плотности нормированного нормального распределения:
f (x) |
|
|
1 |
|
|
|
u2 |
|
||||||||
= |
|
|
|
|
|
|
|
|
exp(− |
2 |
) . |
(1.11) |
||||
|
|
|
|
|
|
|
|
|||||||||
|
|
2π |
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||
Тогда функция нормального распределения приобретает вид |
||||||||||||||||
|
|
1 |
|
|
|
u |
|
|
2 |
И |
|
|||||
F(x) = |
|
|
|
|
∫exp(−u |
|
)du . |
(1.12) |
||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
2π |
−∞ |
|
2 |
|
|
||||||||
Этот интеграл также |
|
|
не |
|
|
|
Д |
элементарные |
||||||||
|
|
|
выражается через |
|||||||||||||
функции, но его можно вычислить через специальные (стандартные)
функции Ф(u) и Ф*(u), представляющие собой |
распределение |
|||
случайной величины |
~ |
с параметрами sx = 1 и x = 0. Они связаны |
||
x |
||||
между собой соотношением |
|
|
||
|
|
Ф*(u) = 0,5 +Ф(u) . |
(1.13) |
|
|
|
|
А |
|
Функции Ф(u) Ф*(u) та улированы и представлены в виде |
||||
таблиц в различных |
сточн ках [12]. Отметим одно из интересных |
|||
|
|
б |
|
|
свойств функции Ф*(u): Ф*(− u) = 1 − Ф*(u). |
|
|||
Наиболее существенный недостаток нормального закона − |
||||
и |
|
|
||
асимптотическое продолжение его в область отрицательных значений |
||||
случайной величиныС. Однако эта область оценивается очень большими значениями u > 5 (табл. 1.1), которые соответствуют крайне малой вероятности реализации случайных величин.
1.4.Параметры метода расчёта по допускаемым напряжениям
Вклассическом методе расчёта прочности по допускаемым напряжениям исходили из соотношения между максимальным напря-
жением σmax, которое определяли в результате расчёта, и допускаемым значением [σ] в виде условия прочности:
14
σmax ≤ [σ]= |
|
, |
|
R |
(1.14) |
||
|
k |
|
|
где k ≥ 1 − коэффициент запаса прочности.
Для вычисления напряжений нагрузочного эффекта σmax применяли простые линейные функции теории упругости (например,
σmax = M/W), связывающие внешние усилия (например, изгибающий момент M) от эксплуатационных (нормативных) нагрузок и геометрические характеристики сечений (например, момент сопротивления сечения W). Тем самым коэффициент запаса k
определялся отношением среднего сопротивления к величине σmax. Сопротивления бетона и арматуры железобетонных конструкций значительно различаются, поэтому применяли два коэффициента
запаса прочности, которые в общем случае не были равны друг другу
принимали равными соответственноА1250 иИ1600 кгс/см2 . Результаты конструктивного расчёта, выполненного по
и должны были быть не меньше нормируемых величин. Так, по
нормам 1934 г., для бетона марок R = 110 кгс/см2 и R = 170 кгс/см2 допускаемые напряжения составлялиДсоответственно 50 и 70 кгс/см2.
Для арматуры сталей Ст.3 и Ст.5 допускаемые напряжения
нормируемых вел ч н k = 1,6… 2,2 в зависимости от вида нагрузок).
допускаемым напряжениям, часто значительно отличались от опытных значений (напримерб, для железобетонных конструкций фактический коэффициентизапаса составлял k = 2,2… 3 против
Одна из пр ч н расхождений заключалась в том, что
допускаемые напряжен я в конструкции принимали по средним или
близким к ним значениям прочности материала при условии его
работы в упругой стадии. Вероятность изменения нагрузок,
большинства свойств материалов, |
условий эксплуатации, а также |
|
неточности классическойС |
теории учитывали, по существу, единым |
|
коэффициентом запаса, |
так как |
закономерности распределения |
случайных величин и событий, характеризующих перечисленные факторы, были ещё мало изучены.
Заменим в условии (1.14) допускаемое напряжение [σ] на среднее значение (математическое ожидание) несущей способности R (как функции прочностных характеристик конструкции), а напряжение σmax − на среднее значение усилия от внешней (эксплуатационной) нагрузки Q, от действия которой возникает это напряжение. Запишем выражение для коэффициента запаса классического метода расчёта в виде, удобном для последующего анализа:
15

|
|
|
|
|
|
|
|
|
|
|
R |
. |
(1.15) |
||
k = k |
= |
|
|||||
|
|||||||
|
|
|
Q |
|
|||
Детерминированную величину отношения математических ожиданий прочности и нагрузки называют статистическим [16] или общим коэффициентом запаса, не являющимся случайной величиной [55]. В сущности, оценить надёжность конструкции только по вели-
чине математического ожидания коэффициента запаса k без учёта вероятностной природы нагрузок и прочностных свойств материалов невозможно.
Метод расчёта по допускаемым напряжениям имеет в основном историческое значение, несмотря на то, что ещё применяется в ряде стран, так как представляет собой простое практическое средство,
чтобы гарантировать достаточно малую вероятность отказа. Недостатки классического метода устранялись постепенно, в течение длительного времени после обнаружения и исследования закономерностей в изменчивости не только физических свойств материалов, но и внешних воздействий.
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
1.5. Метод двух моментов и вероятностная интерпретация |
|
|
|
||||||||||||
|
|
|
|
|
|
|
Д |
|
|
|
|
|
|
||
|
|
|
|
общего коэффициента запаса |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
||
Если изменч вость нагрузки и прочности известна, например, в |
|||||||||||||||
виде дисперсий s2 |
s2 |
б |
|
|
|
|
|
|
|
|
|||||
ли коэффициентов вариации v |
= s |
Q |
Q и |
||||||||||||
|
|
|
Q |
|
R |
|
|
|
Q |
|
|
|
|
||
vR = sR |
|
|
, то иногдаиоценить надёжность можно по |
изменчивости |
|||||||||||
R |
|||||||||||||||
функции, которую называют резервом прочности: |
|
|
|
|
|
|
|||||||||
|
|
|
С |
|
~ |
|
|
|
|
(1.16) |
|||||
~ |
|
|
|
S = R −Q , |
|
|
|
||||||||
и Q − случайные величины несущей способности и нагрузоч- |
|||||||||||||||
где R |
|||||||||||||||
ного эффекта, имеющие одинаковые размерности.
Основными вероятностными характеристиками этой функции являются математическое ожидание S = R −Q и дисперсия
sS2 = sR2 + sQ2 (при отсутствии корреляционной связи между нагрузкой
и несущей способностью). Величину β, обратную коэффициенту вариации функции (1.16) vS = sS  S , А.Р. Ржаницын назвал характери-
S , А.Р. Ржаницын назвал характери-
стикой безопасности (рис. 1.4), которая при распределении исходных данных по нормальному закону определяется по формуле [55]
16

|
|
|
|
|
|
R −Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
β = |
|
S |
|
= |
|
|
|
= |
|
|
|
k |
−1 |
|
|
. |
(1.17) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
sS |
s2 |
+ s2 |
|
|
|
|
|
2v2 |
+ v2 |
|
|
|
||||||||
|
|
|
|
k |
|
|
|
||||||||||||||
|
|
|
|
|
|
R |
|
Q |
|
|
|
|
|
|
|
R |
|
Q |
|
|
|
f(S)
Рис. 1.4. Плотность распределения случайной величины S~
0 βsS S |
S |
|
|
|
~ |
Вероятность отказа (риск) или вероятность отрицательного зна-
|
|
|
|
|
~ |
|
|
|
|
|
|
определяется |
|
чения резерва прочности S при известном значении β |
|||||||||||||
из формулы |
|
|
|
|
~ |
|
|
|
|
|
(1.18) |
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
PQ = P(S < 0) = 0,5 −Ф(β), |
|||||||||
|
1 |
|
β |
x2 |
|
|
|
|
|
|
И |
|
|
где Ф(β) = |
|
|
0∫exp(− |
2 )dx |
|
|
|
|
|
|
|||
2π |
|
− интеграл вероятности |
или функция |
||||||||||
Лапласа переменной |
~ |
|
|
|
|
, соответствующий |
стандартной |
||||||
|
|
|
|
||||||||||
x = (S − S ) s |
S |
||||||||||||
функции Ф(u). |
|
|
|
|
|
|
|
Д |
|
||||
|
|
|
|
выше свойства функции Ф*(u) (1.13) |
|||||||||
С учётом |
|
отмеченного |
|||||||||||
можно также записать |
|
|
А |
|
|
||||||||
|
|
~ |
|
|
|
|
(1.19) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
PQ б= P(S < 0) =1−Ф*(β) . |
|||||||||
Вероятность безотказной работы или надёжность конструкции |
|||||||||||||
PR =1− PQ . |
|
и |
|
|
|
|
|
|
|
||||
стью случайнойСвеличины S~ . Метод оценки надежности посредством коэффициента β получил название метода двух моментов, поскольку
Индекс безопасности β является стандартизированной вероятно-
для его определения используются по две характеристики случайных величин R~ и Q~ .
В табл. 1.1 приведены некоторые значения β и соответствующие
им значения функции Ф*(β = u), которые можно использовать в расчётах на безопасность.
17

Таблица 1.1
Соотношение между индексом безопасности и вероятностью отказа
β |
Ф*(β) |
β |
Ф*(β) |
β |
Ф*(β) |
β |
Ф*(β) |
0,0 |
0,5000 |
1,0 |
0,8413 |
2,0 |
0,97725 |
3,0 |
0,99865 |
0,1 |
0,5398 |
1,1 |
0,8643 |
2,1 |
0,98214 |
3,1 |
0,99903 |
0,2 |
0,5793 |
1,2 |
0,8849 |
2,2 |
0,98610 |
3,2 |
0,99931 |
0,3 |
0,6179 |
1,3 |
0,9032 |
2,3 |
0,98928 |
3,3 |
0,99952 |
0,4 |
0,6554 |
1,4 |
0,91924 |
2,4 |
0,99180 |
3,4 |
0,99966 |
0,5 |
0,6915 |
1,5 |
0,93313 |
2,5 |
0,99379 |
3,5 |
0,99977 |
0,6 |
0,7257 |
1,6 |
0,94520 |
2,6 |
0,99534 |
3,6 |
0,99984 |
0,7 |
0,7580 |
1,7 |
0,95543 |
2,7 |
0,99653 |
3,7 |
0,99989 |
0,8 |
0,7881 |
1,8 |
0,96407 |
2,8 |
0,99744 |
3,8 |
0,99993 |
0,9 |
0,8159 |
1,9 |
0,97128 |
2,9 |
0,99813 |
3,9 |
0,99995 |
Пример 1.2. При общем коэффициенте запаса k = 1,4 и коэффициентах вариации нормально распределённых напряжений в растянутой стенке резервуа-
ра vQ = 0,12 и прочности бетона на растяжение vR = 0,135 определить вероят- |
||||
ность отказа PQ в виде образования трещин. |
||||
По |
|
формуле (1.11) определяем характеристику безопасности |
||
β= (1,4 −1) |
|
|
|
Д |
|
1,420,1352 + 0,122 |
= 1,787. По табл. 1.1 имеем Ф*(β) = 0,963. Вероят- |
||
ность отказа PQ = 1 – 0,963 = 0,037. |
|
|||
Пример 1.3. Элемент стальной фермы в результатеИизменчивости нагруз- |
||||
ки Q по нормальному закону испытывает растягивающие напряжения с парамет- |
||||
рами σt = |
246 МПа; sσt = 28 МПа и сжимающие напряжения σc = 70 МПа; |
|||
|
|
|
б |
|
sσc = 10,5 МПа. Среднее значение прочности стали составляет R = 350 МПа. Оп- |
||||
ределить максимальное значение среднего квадратического отклонения прочности, |
|
и |
|
при котором гарантируется вероятностьАезотказной работы не менее |
PR = 0,999. |
Среднее эффект вное напряжение (нагрузочного эффекта) Q = 246 – 70 = |
|
С |
выражением |
= 176 МПа, а его стандартное отклонение определяется |
|
sσ = 
 282 +10,52 = 29,9 МПа. С помощью таблиц для нормального распределения (см. табл. 1.1) находим при PR = 0,999 значение β = 3,09. Подставляя это значение в уравнение (1.17), получаем 3,09 = (350 – 176)/
282 +10,52 = 29,9 МПа. С помощью таблиц для нормального распределения (см. табл. 1.1) находим при PR = 0,999 значение β = 3,09. Подставляя это значение в уравнение (1.17), получаем 3,09 = (350 – 176)/ 

уравнение относительно sR, имеем sR = 47,7 МПа.
Решая уравнение (1.17) относительно k, выражение для общего коэффициента запаса
1+ 1−(1−β2v2 )(1−β2v2 )
k = 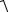 2 R2 Q .
2 R2 Q .
1−β vR
Пример 1.4. Определить требуемый общий коэффициент запаса k при
расчётных параметрах примера 1.2 и характеристике безопасности β = 3. Общий коэффициент запаса определяем по формуле (1.20):
k = (1+ 
 1−(1−320,1352 )(1−320,122 )
1−(1−320,1352 )(1−320,122 )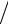 (1−320,1352 )= 1,82.
(1−320,1352 )= 1,82.
18

Из формулы (1.20) видно, что k зависит от вероятностных характеристик нагрузки и прочности, а также от численного значения
коэффициента β, характеризующего гауссовский уровень надёжности. Чем больше характеристика безопасности β, тем меньше вероятность
разрушения и больше надёжность. |
Например, |
если vQ = vR = 0,2 и |
β = 3 (вероятность разрушения |
0,999), то |
коэффициент запаса |
k = 2,76. Такому же значению коэффициента k соответствует
сочетание vQ = vR = 0,3 и β = 2 (вероятность разрушения 0,977). |
|
Отсюда следует вывод, что одно и то же зна |
чение коэффициента |
запаса может соответствовать разным уровням надёжности конструкций. Это означает, что статистический коэффициент запаса
критерием надёжности не может быть. |
И |
−∞ |
Плотность распределения вероятностей случайной величины S (1.19) определяется как для функции двух независимых случайных
величин R и |
Q из выражения |
Д |
|
|
~ |
|
|
|
|
|
|
∞ |
|
(1.21) |
|
p(S) = |
∫ p(S +Q) p(Q)dQ, |
||
где p(S +Q) |
− плотность |
|
А |
с аргументом |
распределения прочности |
||||
(S + Q).
Практически при лю ых законах распределения независимых
Имеется такжеизав с мость между характеристиками безопасности β и обеспеченности или дальности расчётных значений несу-
величин R~ и Q в качестве характеристики надёжности конструкции
можно рассматривать коэфф циент безопасности в виде выражения |
||
(1.17). |
С |
б |
|
||
щей способности и нагрузки βR и βQ. Для получения этой зависимости и ответа на вопрос, в какой мере выбор расчётных величин определяет надёжность, воспользуемся следующим приёмом [54].
Разделим случайные величины равенства (1.16) |
R и Q на соот- |
||
|
|
|
~ |
ветствующие расчётные значения параметров R и Q. Получим слу- |
|||
чайные безразмерные величины |
и q = Q Q , |
(1.22) |
|
r |
= R R |
||
~ |
~ |
~ |
|
расчётные значения которых будут единичными, т.е. r = q = 1, а к о- эффициенты вариации и дальности расчётных значений в силу своей
относительности − тождественными: vR = vr; vQ = vq; βR = βr; βQ = βq. Надёжность Pr (r > q) при нормальном распределении всех случайных
величин соответствует вероятности безотказной работы 1 − Pq , где Pq
19

определяется |
по формуле (1.18), а характеристику |
безопасности |
||||||||||||
β = |
|
r |
−q |
можно преобразовать, принимая |
r |
=1+βr sr , q =1−βq sq |
||||||||
|
|
|
|
|
||||||||||
sr2 + sq2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
и χ = sr sq , в более удобное для анализа выражение |
|
|||||||||||||
|
|
|
|
|
|
β = |
χβr +βq |
. |
(1.23) |
|||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
1+ χ2 |
|
||||||
Аналогичное выражение получено в работе [22] при описании случайных величин логнормальным законом. При этом случайные исходные величины рассматривались в виде ln ~r и ln q~ . Следует от-
метить, что при аппроксимации эмпирических распределений теоретическими, как правило, конкурентоспособными оказываются не-
териев, по которым можно бы было выбиратьИодин наиболее подходящий закон, нет. В математической статистике есть лишь критерии,
сколько законов распределения и из них выбирается тот, который
удобнее для решения задачи. Т.е. распределение одной и той же слу-
чайной величины в различных задачах может быть аппроксимировано
различными законами. Это совершенно естественно, поскольку кри-
отвергающие неприемлемые законы. Желательно, чтобы принимае- |
|
мые законы распределения не противоречилиД |
физическому смыслу |
рассматриваемых величин, хотя иногда можно даже пойти на такое |
|
противоречие, если оно не приводит к значительным погрешностям. |
|||
|
|
А |
|
Преимущество логнормального закона прежде всего в том, что он со- |
|||
|
С |
|
|
ответствует физическомубсмыслу рассматриваемых случайных вели- |
|||
чин, распределен я которых ограничены слева нулём и имеют поло- |
|||
жительную асимметриюи(см. рис. 1.2). |
|
||
Продифференцировав β по χ и приравняв производную нулю, |
|||
получим условие максимальной вероятности безотказной |
работы |
||
βmax = |
β2r +β2q |
, которое достигается при χ = βr/βq. Из (1.23) |
видно, |
что надёжность зависит не только от обеспеченности расчётных значений параметров, но и отношения характеристик изменчивости прочности и нагрузки.
Имеются предложения о нормировании характеристики безо-
пасности β, связь которой с расчётными значениями можно представить в следующем виде:
Q = Q (1+αQβvQ ); |
(1.24) |
20
