
- •ВВЕДЕНИЕ
- •1. РАСЧЕТ КАК ИНСТРУМЕНТ ОБЕСПЕЧЕНИЯ НАДЕЖНОСТИ КОНСТРУКЦИЙ
- •1.1. Изменчивость расчётных параметров
- •1.2. Применение теории вероятностей для учета изменчивости
- •1.3. Особенности нормального закона распределения
- •1.4. Параметры метода расчёта по допускаемым напряжениям
- •1.6. Вероятностная зависимость параметров исходных данных
- •1.7. Метод расчёта по разрушающим нагрузкам и условный коэффициент запаса
- •1.8. Расчётные параметры метода предельных состояний
- •1.9. Совершенствование метода предельных состояний
- •1.10. Учёт фактора времени
- •2.3. Постоянные нагрузки
- •2.4. Полезные нагрузки на перекрытия
- •2.5. Снеговые нагрузки
- •2.6. Ветровые нагрузки
- •2.7. Температурные климатические воздействия
- •2.8. Крановые нагрузки
- •2.9. Аварийные ударные воздействия
- •2.11. Сочетания нагрузок
- •3. ИЗМЕНЧИВОСТЬ СВОЙСТВ СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ
- •3.1. Основные положения
- •3.2. Строительные стали
- •3.3. Бетоны
- •3.4. Строительные растворы
- •3.5. Кирпич и каменная кладка
- •3.6. Древесина
- •3.7. Грунты
- •4. ЗАДАЧИ РАСЧЁТА КОНСТРУКЦИЙ НА НАДЁЖНОСТЬ
- •4.1. О надёжности ограждающих конструкций при расчёте на теплопередачу
- •4.2. Вероятностная оценка прочности железобетонных элементов по нормальным сечениям при изгибе
- •4.3. Изменчивость несущей способности изгибаемой конструкции
- •4.4. Неопределенность расчетных моделей конструкций
- •Библиографический список
4.2. Вероятностная оценка прочности железобетонных элементов по нормальным сечениям при изгибе
Закон распределения несущей способности M~ сечений изгибаемых конструкций, выполненных из однородного материала, обычно соответствуют закону распределения прочности данного материала f (R), так как их взаимосвязь описывается простыми линейными
зависимостями вида M~ = kR~ . Характеристики случайной величины R~
и соответственно функции M~ легко получить опытным путём, если пренебречь изменчивостью размеров сечений.
Несущая способность железобетонных конструкций характери-
зуется изменчивостью нескольких сложно взаимодействующих эле-
вероятностного расчёта. В таких случаяхИособую важность имеют теоретические методы расчёта надёжности, в частности, метод двух моментов (здесь момент − числовая характеристика случайной вели-
ментов. Из-за разнообразия взаимодействия затрудняется экспери-
ментальная оценка случайной величины несущей способности M~ же-
чины или функции). Практическая Дценность метода заключается в том, что первые два момента, т.е. математическое ожидание x и стан-
лезобетонных конструкций, а также точность оценки надёжности и
мени. Метод хорошо согласуетсябс принятым в отечественных нормах методом расчёта по предельным состояниям и особенно эффективен
дартное отклонение s, оптимально характеризуют случайную величи- |
||
ну |
~ |
А |
x |
и всегда могут быть найдены при незначительных затратах вре- |
|
при оценке надёжности по отказам, связанным с исчерпанием несу- |
|
щей способности. |
и |
|
|
Для расчёта несущей способности железобетонных конструкций |
|
в нормах применяетсяСметод сечений. Несущая способность изгибае- |
|
мых конструкций характеризуется прочностью нормальных и на- |
|
клонных сечений. Для оценки прочности нормальных сечений по методу предельных состояний используют два основных уравнения, полученных из статических условий равновесия. Во-первых, значения изгибающих моментов всех внутренних сил относительно центров тяжести растянутой и сжатой зон сечения определяют из тождественных уравнений, которые представим в следующем виде
Mb = Rb f1(ξ) и M s = Rs f2 (ξ), |
(4.15) |
где Rb и Rs − расчётные сопротивления бетона сжатой зоны и растянутой арматуры; f1(ξ) и f2(ξ)− функции, характеризуемые размерами се-
189
чения, сжатой зоны бетона и степенью армирования; ξ − относительная высота сжатой зоны.
Для конструкций прямоугольного сечения шириной b, рабочей высотой h0 и с коэффициентом армирования µ (при одиночном армировании) функции f(ξ) имеют вид
f |
(ξ)= bξh |
2 |
|
− |
ξ |
|
и f |
|
(ξ)= bµh |
2 |
|
ξ |
(4.16) |
|
|
1 |
2 |
|
|
|
1− |
. |
|||||||
1 |
0 |
|
|
|
|
2 |
|
0 |
|
2 |
|
|||
Второе уравнение получают из условия равновесия нормальных |
||||||||||||||
сил |
|
|
|
ξRb |
= µRs . |
|
|
|
|
(4.17) |
||||
|
|
|
|
|
|
|
|
|||||||
Условие тождественности Mb ≡ Ms должно соблюдаться и при |
||||||||||||||
вероятностных расчётах, когда моменты Mb |
и M s |
являются случай- |
||||||||||||
|
|
|
|
|
|
|
|
|
~ |
|
|
~ |
|
|
а их характеристики (математическое ожиданиеИи дисперсия) легко получаются из нормативных данных. В практических расчётах веро-
ными. Обычно при построении вероятностных зависимостей этим условием пренебрегают, что приводит часто к неверным выводам. Как правило, выражения (4.15) рассматривают в виде функции случайных
аргументов R~b или R~s , распределения которых близки к нормальным,
ятностные характеристики прочности бетона и арматуры определяют |
|||||||
|
|
|
|
|
|
Д |
|
из расчётных или нормативных зависимостей сопротивлений, имею- |
|||||||
щих вид |
|
|
|
|
А |
(4.18) |
|
|
|
|
|
|
|||
|
|
|
|
||||
|
|
R = R(1−βv). |
|||||
Иногда |
изменч востью |
других параметров (в том числе и |
|||||
ξ = µRs Rb ) |
|
б |
|
расчётах |
|||
пренебрегают, |
спользуя в приближённых |
||||||
только их математическиеиожидания. В более точных моделях слу- |
|||||||
|
~ |
~ |
|
|
|
|
|
чайные моменты Mb и |
M s считают функцией двух или нескольких |
||||||
|
С |
|
|
|
|
|
~ |
(изменчивостью геометрических размеров зачастую можно пренебречь) случайных величин-аргументов. В этом случае о моменте Mb
судят по свойствам случайных величин R~b и ξ = µR~s  R~b , а о величине M~ s − по характеристикам R~s и ξ. Такой подход эффективен, когда законы распределения случайных аргументов, в том числе и ξ , известны. Однако точное выражение дисперсии случайной величины ξ
R~b , а о величине M~ s − по характеристикам R~s и ξ. Такой подход эффективен, когда законы распределения случайных аргументов, в том числе и ξ , известны. Однако точное выражение дисперсии случайной величины ξ
для общего случая получить невозможно, поэтому расчёт сводится к численному интегрированию сложных функций, т.е. также практически становится приближённым [58]. Наиболее распространена приближённая модель с использованием линеаризации расчётных фор-
190

мул и разложения их в ряд Тэйлора. Такой приём использован во многих отечественных и зарубежных исследованиях [57, 64, 73].
Возможен другой подход, упрощающий расчёт и позволяющий избежать каких-либо противоречий. Рассмотрим выражения моментов (4.15) как случайные функции, для которых возможны реализации
двух видов в зависимости от случайного аргумента ξ: при ξ≤ ξR и ξ> ξR. Согласно теории случайных функций, каждая реализация M~b и M~ s есть обычная функция неслучайного аргумента ξ1, которая при фиксированном значении является случайной величиной с числовыми характеристиками, эквивалентными характеристикам R~b и R~s . Исхо-
дя из этого, подставим выражение (4.18) в уравнения (4.15) и, пренебрегая изменчивостью геометрических параметров и армирования сечения, получим простые линейные зависимости несущей способности
|
|
|
|
|
|
|
|
|
|
|
~ |
или |
~ |
|
|
|
|
|
||||
от одного случайного аргумента Rb |
|
Rs , которые по аналогии с |
||||||||||||||||||||
выражением (4.18) можно записать в общем виде |
|
|||||||||||||||||||||
|
|
|
|
|
|
M = |
|
(1−βvM )= |
|
|
−βsM . |
(4.19) |
||||||||||
|
|
|
|
|
M |
M |
||||||||||||||||
Для определения значения vM раскроем функцию (4.19) отдельно |
||||||||||||||||||||||
по бетону и арматуре: |
|
|
|
|
|
|
|
И |
|
|||||||||||||
|
Mb = |
Rb f1( |
|
)−βsb f1(ξ) и M s |
= |
Rs f2 ( |
|
)−βss f2 (ξ). |
(4.20) |
|||||||||||||
|
ξ |
ξ |
||||||||||||||||||||
Выражения sb f1(ξ) и ss f2 (ξ) |
Д |
|
||||||||||||||||||||
являются стандартами изменчиво- |
||||||||||||||||||||||
~ |
~ |
|
|
|
|
|
|
|
|
sM |
= dM dβ), которые равны из усло- |
|||||||||||
сти Mb и |
M s (в общем случае |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
||
вия тождественности Mb ≡ Ms. Из их равенства определяется значение |
||||||||||||||||||||||
ξ1 для стандартов |
зменчбвости Mb и M s |
по формуле |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
~ |
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
иξ = µss |
= ξ vs . |
|
|
|
|
|
|
|
(4.21) |
|||||||||
|
|
|
|
|
1 |
|
sb |
|
vb |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Полученная зависимость остаётся справедливой и для более |
||||||||||||||||||||||
сложных случаевСармирования и форм сечений. Это подтверждается |
||||||||||||||||||||||
выражениями, связывающими коэффициенты вариации и относи- |
||||||||||||||||||||||
тельной высоты сжатой зоны: |
|
|
|
|
|
|
|
|
(1− 0,5ξ)ξ |
|
|
|||||||||||
|
v |
|
|
= v |
|
1− 0,5ξ |
или v |
|
= v |
. |
(4.22) |
|||||||||||
|
|
|
s 1− 0,5ξ |
|
|
|||||||||||||||||
|
|
M |
|
|
|
M |
|
|
|
|
b (1− 0,5ξ)ξ |
|
||||||||||
Тождественность M~b и M~ s обеспечивается также учётом корреляции или зависимости случайных величин R~b и R~s в рамках нор-
мального сечения. Обычно эти величины считают независимыми, однако в расчётном сечении в явном виде прослеживается их линейная взаимосвязь, которая описывается вторым статическим условием рав-
191
новесия (4.17) нормальных сил. В вероятностном виде это условие можно представить как ξR~b = µR~s или N~ = ξRb −µ~R~s = 0 .
Учитывая нормальное распределение исходных случайных переменных R~b и R~s , вероятностную оценку условия (4.17) можно по-
лучить при известных математических ожиданиях Rb, Rs и стандартных отклонениях sb, ss методом двух моментов через характеристику
безопасности β:
β = Nb − |
|
s |
|
|
|
ξRb −μRs |
|
|
|
|
|
N |
= |
|
|
|
. |
|
(4.23) |
||||
|
|
|
|
|
|
||||||
ssb |
|
|
ξ2 sb2 −2ρξμsb ss +μ2 |
ss2 |
|
|
|
||||
Нетрудно заметить, что параметр β представляет собой обрат- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
~ |
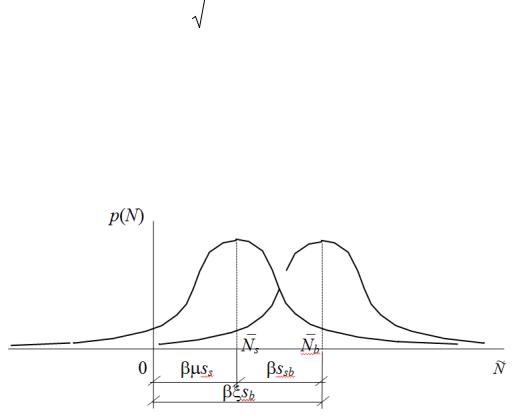
ную величину коэффициента вариации случайной величины N (рис. |
|||||||||||
4.1). |
|
|
|
|
|
|
И |
|
|
||
Вероятность безотказности при известном значении β определя- |
|||||||||||
ется из формулы (4.7) |
|
|
|
Д |
|
|
|
|
|||
|
|
|
PN = 0,5 +Ф(β). |
|
|
|
|
(4.24) |
|||
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
||
и |
|
|
|
|
|
|
|
||||
С |
|
|
|
|
|
|
|
|
|
||
Рис. 4.1. Распределение случайной величины N |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
~ |
|
~ |
коэффици- |
При положительной корреляционной связи Rb и |
Rs |
||||||||||
ент корреляции ρ = 1 и из выражения (4.23) получается простая зависимость для вероятностной оценки условия прочности
β = |
ξRb −µRs . |
(4.25) |
|
ξsb −µss |
|
Аналогичное решение можно получить также для граничных значений ξR с целью обеспечения в прочностном расчёте условия
ξ1 ≤ ξR. Для этого можно воспользоваться эмпирической зависимостью, приведённой в работе [58]:
192
ξR = (1150 – 9,6 Rb )/(1000 + Rs ). |
(4.26) |
|
~ |
~ |
|
Учитывая, что изменчивость случайных величин в формуле (4.26) характеризуется стандартами ξRss и 9,6sb (в МПа), в качестве характеристики обеспеченности расчётного значения ξR также используем параметр β.
В то же время для определения ξR применяется следующая эмпирическая зависимость:
ξR = |
|
0,8 |
|
, |
(4.27) |
1+ εs,el |
|
||||
|
εb,ult |
|
|||
где εs,el = Rs/Es и εb,ult = 0,0035.
При выводе формулы (4.27) эмпирические коэффициенты были |
|
выбраны таким образом, чтобы значения ξR, определяемые из расчёт- |
|
|
И |
ных или средних значений Rs и Rb, получались одинаковыми [45]. Это |
|
означает, что изменчивостью ξR при определении по формуле (4.27) |
|
можно пренебречь. |
Д |
|
|
Вероятностная оценка (4.25) необходима для уточнения числен- |
|
ных значений ξ в приграничной зоне. Например, при учёте условия
ξ ≤ ξR для этого рекомендуется зависимость |
|
ξ = Pξ1 + PRξR. |
(4.28) |
|
Вероятность P (ξ1 ≤ ξR ) определяется по формулам (4.24), (4.25) |
||||
при |
|
= ξR. Невыполнение этого условия оценивается вероятностью |
|||
ξ |
|||||
PR = 1 − P. |
|
|
А |
||
|
В целом при звестных значениях коэффициента армирования |
||||
µ, средних значен ях |
|
б |
|||
|
стандартных отклонениях или коэффициентах |
||||
вариации сопротивленийибетона Rb, sb или vb и арматуры Rs, ss или vs |
|||||
для определения среднего значения и коэффициента вариации (стан- |
|||||
дартного отклонения) |
несущей способности М и vM (sМ) железобе- |
||||
|
|
|
С |
|
|
тонного элемента рекомендуется следующий алгоритм:
1)по средним значениям Rb и Rs из формулы (4.26) или по расчётным значениям Rb и Rs из формулы (4.27) определяется ξR ;
2)по средним значениям Rb и Rs из формулы (4.17) вычисляет-
ся ξ;
3)по формуле (4.21) определяется в первом приближении ξ = ξ1;
4)по формулам (4.25) и (4.24) определяются β, P и PR;
5)по формуле (4.28) уточняется значение ξ;
6)по формуле (4.22) определяется vM;
193

7) по средним значениям параметров из формул (4.15) и (4.16)
вычисляется М и, если необходимо, sМ.
Для сравнения выполнен расчёт характерного примера по данным работы [58] при различных значениях коэффициента армирова-
ния µ: b = 0,2 м; h0 = 0,385 м; Rb = 13,5 МПа; Rs = 375 МПа;Rb = 29,2 МПа; sb = 3,94 МПа; Rs = 446 МПа; ss = 28,81 МПа.
По формуле (4.22) определено граничное значение относительной высоты сжатой зоны бетона ξR = 0,596, которое принимаем по-
стоянным при любых значениях β.
При расчётных сопротивлениях Rb и Rs определены расчётные значения Мп метода предельных состояний. Характеристика безопасности для вероятностной оценки метода предельных состояний рас-
считывалась по формуле χ = ( М – Мп)/sМ. |
И |
Сравнительные результаты расчётов, выполненных с учётом фор- |
|
мул (4.24) и (4.25) (в знаменателе− по работе [58]), приведены в табл. 4.2.
|
|
|
Сравнение результатов расчёта |
|
Таблица 4.2 |
|||||||
|
|
|
|
|
|
|||||||
Параметры, |
|
|
|
Коэффициент армирования µ |
|
|
||||||
|
|
|
|
|
|
|
Д |
|
|
|
||
ед. изм. |
0,004 |
|
|
0,012 |
|
0,024 |
0,036 |
|
0,048 |
|
0,06 |
|
М, кН м |
51,3/54 |
|
|
144/150 |
|
259/268 |
345/339 |
|
362/360 |
|
362/361 |
|
|
м |
3,4/4 |
|
|
9,8/11 |
|
18,8/16 |
26,8/29 |
|
33,9/39 |
|
40/40 |
sМ, кН |
|
|
|
|
|
А |
|
|
|
|
|
|
Мп, кН м |
42/43 |
|
|
111/116 |
|
167/198 |
167/203 |
|
167/203 |
|
167/203 |
|
|
|
|
|
|
б |
|
|
|
|
|
||
χ |
|
2,8/2,7 |
|
|
3,4/3,1 4,9/4,4 |
6,6/4,7 |
|
5,7/4 |
|
4,9/3,9 |
||
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для всех случаев армирования (кроме µ = 0,036) получены абсо- |
||||||||||||
лютные значения β более 4. Вероятности P или PR соотношений ξ1 и |
||||||||||||
ξR при этом практическиСравны 1. При µ = 0,036 вероятность P = 0,847 |
||||||||||||
(PR = 0,153) и по |
уточнённым значениям ξ |
были |
получены |
|||||||||
М = 348 кН м и sМ = 30,9 кН м.
Можно отметить хорошее совпадение результатов расчёта ос-
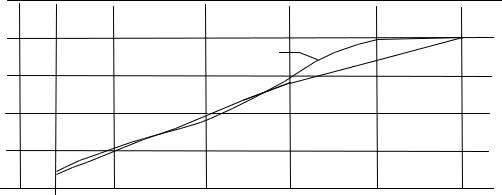
новных вероятностных характеристик М и sМ (рис. 4.2). Несовпадение результатов расчёта расчётного усилия Мп при
больших значениях µ (в области ξ ≥ ξR) объясняется различным подходом к определению ξR. По сравнению с результатами работы [58]
(сплошная линия) графическая зависимость sМ – µ получилась более чёткой.
194
sМ
По [58]
0 |
0,004 |
0,012 |
0,024 |
0,036 |
0,048 |
0,06 |
µ |
|
|
Рис. 4.2. Зависимость sМ – µ |
|
|
|
||
|
|
И |
Здесь коэффициенты вариации для тяжёлого бетона vb = 0,135, |
||
для арматуры класса А 400 vs = 0,1. Так, для бетона В20 получено |
||
|
Д |
|
Rb = 19,2 МПа; sb = 2,59 МПа, для арматуры А 400 Rs = 466,5 МПа; |
||
ss = 46,7 МПа. |
А |
|
Пример 4.1. |
|
|
Определить вероятность отказа (исчерпания прочности по |
||
нормальному сечению) сборной железобетонной плиты пролётом l0 = 5,8 м плоского совмещённого покрытия при действии постоянной и снеговой нагрузок и следующих исходных данных: район строительства г. Омск; класс бетона пли-
рубероида, утеплитель толщиной 20 см из минераловатных плит плотностью 200 кг/м , керамзитовая засыпка для разуклонки кровли средней толщиной 10 см из керамзита плотностью 600 кг/м3 и четырёхслойная рубероидная кровля.
ты В20; класс стали А 600; номинальная ширина плиты bпл = 1,5 м, толщина пол- |
|||
ки hп = 3 см, суммарная (усреднённая по высоте) толщина рёберb = 15 см; высо- |
|||
та плиты h = 30 см; расстоян е от центра тяжести арматуры As до крайнего рас- |
|||
тянутого волокна a |
|
б |
|
= 2 см. Структура покрытия: плита, пароизоляция из слоя |
|||
3 |
|
и |
|
|
С |
|
|
Рассматриваем снеговую нагрузку в районе г.Омска (см. примеры 2.2 –
2.4) при µ = 1. Двойной экспоненциальный закон (2.30) для распределения максимума за 25-летний период при z = 0,34 кПа и u25 = 1,59 кПа записывается в ви-
|
|
|
|
0,5 |
~ |
|
|
|
|
|
− ST + ln 25 |
|
|||
де R(S |
25 |
)= exp |
− exp |
|
|
|
. Среднее значение ежегодных максимумов |
|
|
||||||
|
|
|
|
0,34 |
|
|
|
|
|
|
|
|
|
|
|
составляет S1 = 0,7 кПа (II район, табл. 2.14), среднее максимальное значение 25-летних периодов S25 = 1,8 МПа (III район, табл. 2.13) и стандартное отклонение sS = 0,44 кПа. Эти параметры используются при аппроксимации распределения снеговой нагрузки нормальным законом.
Постоянную нагрузку считаем распределённой по нормальному закону с функцией распределения R(q)=Ф[(g~ − g )/ sg ], где g − среднее значение; sg −
стандарт суммарной постоянной нагрузки.
195
Сбор постоянных нагрузок на покрытие
|
Вид нагрузки |
gni, кПа |
γf |
gi, кПа |
1. Вес плит покрытия |
2,5 |
1,1 |
2,75 |
|
2. |
Вес пяти слоёв рубероида 0,05 5 |
0,25 |
1,3 |
0,325 |
3. |
Вес утеплителя 200 0,2/100 |
0,4 |
1,3 |
0,52 |
4. |
Вес керамзита 600 0,1/100 |
0,6 |
1,3 |
0,78 |
Итого |
3,75 |
|
4,375 |
|
Принимаем g = ∑gni = 3,75 кПа. Согласно разделу 2.2, определяем весо-
вые коэффициенты α1 = 2,5/3,75 = 0,66; α2 = 0,25/3,75 = 0,07; α3 = 0,4/3,75 = 0,11;
α4 = 0,6/3,75 = 0,16. В зависимости от коэффициента надёжности по нагрузке принимаем коэффициенты вариации по табл. 2.6. Для плит покрытия v1 = 0,033, для прочих нагрузок vi = 0,1. Из формулы (2.9) вычисляем коэффициент вариации для постоянной нагрузки vg = 0,03 и стандартное отклонение sg = 0,11 кПа.
Суммарная расчётная нагрузка составляет g0 = 1,8 + 4,375 = 6,175 кПа. По-
гонная нагрузка g = g0bпл = 6,175 1,5 = 9,26 кН/м. Расчётный изгибающий момент |
|||||
при балочной расчётной схеме плиты M = gl02/8 = 38,95 кН м. |
|
|
|||
Расчётные |
сопротивления: бетона |
Rb = 11,5 |
МПа; |
арматурной |
стали |
Rs = 510 МПа. |
|
|
|
|
|
При h0 = h − a = 28 см определяем рабочую продольную арматуру плиты, |
|||||
|
|
И |
|
|
|
необходимую для обеспечения прочности, из расчёта по предельному состоя- |
|||||
нию. |
|
Дграницы |
|
|
|
Проверяем |
положение нижней |
сжатой |
зоны. Так |
как |
|
M < Rbbf′hf′(h0 − 0,5hf′) = 137 кН м, то граница сжатой зоны проходит в полке с
расчётными размерами ширины bf′ = 1,5 м и высоты hf′ = 0,03 м. Коэффициент |
|||
αm |
= M/Rbbf′h02 = 0,03 |
|
А |
ζ = 0,985. Требуемая площадь сечения арматуры |
|||
As |
= M/Rsζh0 = 2,77 см2. Пр н маем 2 14 A 600 при As = 3,08 см2. Коэффициент |
||
|
|
б |
|
армирования µ = As/bh0 = 0,007. |
|
||
|
По табл. 3.5 определяем характеристики прочности бетона: Rb =19,2 МПа; |
||
sb |
и |
|
|
= 2,59 МПа и vb = 0,135. Обеспеченность расчётного сопротивления бетона |
|||
|
С |
|
|
сжатию Pb = 0,9985 при β = (1 − Rb/ Rb)/vb = 2,971. По табл. 3.1 определяем ха-
рактеристики прочности арматурной стали: Rs = 690 МПа; vs |
= 0,09 и ss = 62 МПа. |
||||||||||
Обеспеченность |
расчётного |
сопротивления |
арматуры |
Ps |
= |
0,9981 |
при |
||||
β = (1 − Rs/ Rs)/vs = 2,899. |
|
|
|
|
|
|
|
|
|
||
|
По алгоритму, изложенному в данном разделе, определяем характеристи- |
||||||||||
ки прочности плиты: ξ |
= µb Rs/bf′Rb = |
0,026 < ξR; ξ1 |
= ξ vs/ vb = 0,018; |
||||||||
β |
= ( ξ Rb − |
µ Rs)/(sb |
− |
µss) = 5,69; |
PR |
≈ 1; P |
≈ |
0; |
ξ = |
ξ1 = |
0,018; |
vM |
= vs(1 − 0,5ξ)/(1 − 0,5 ξ) |
= 0,09 и M |
= RsAsh0(1 − |
0,5 ξ) = 58,73 кН м и |
|||||||
sM = 5,28 кН м. Этим значениям несущей способности эквивалентна равномерно распределённая нагрузка qM = 8 M/bплl02 = 9,31 кПа и sqM = 0,84 кПа.
Если As = 2,77 см2, то M = RsAsh0(1 − 0,5 ξ) = 52,82 кН м и обеспеченность расчётного значения несущей способности PM = 0,9982 при
196

β = (1 − M/M)/vM = 2,918, что соответствует обеспеченности расчётных сопротивлений материалов.
Так как распределения случайных величин нагрузок и несущей способности плиты аппроксимированы нормальным законом, надёжность плиты опреде-
ляем по формулам (1.17) и (1.18). При этом β = ( q |
M |
− S − |
g )/ |
2 2 |
2 |
= |
|
|
|
sR + sS |
+ sg |
|
|
= (9,31 − 1,8 − 3,75)/(0,842 + 0,442 + 0,112)1/2 = 3,94, что соответствует вероятности |
||||||
безотказной работы PR = 0,9999.
Выполненный расчёт является приближённым, так как снеговая нагрузка распределяется не по нормальному закону. Используя метод Б. Снарскиса [59], реализованный в отчёте [50], можно уточнить вероятность безотказной работы
плиты. Метод заключается в поиске минимального значения β путём последовательного приближения. В первом приближении задаются значением снеговой нагрузки S = 1,8 + 3,94 0,44 = 3,53 кПа и определяют дальность отказа величин,
распределённых по |
нормальному |
закону, |
из |
выражения βn |
= ( qM − g − |
|||||||
|
|
|
|
|
|
|
|
|
И |
|
|
|
– S)/ sqM2 + sq2 |
|
= (9,31 – 3,75 − 3,53)/0,847 = 2,4. Вероятность реализации при- |
||||||||||
ближённого |
значения S = |
3,53 |
кПа |
вычисляется |
из |
формулы |
||||||
|
|
|
1,59 − S |
|
|
|
|
|
|
|
||
R(S)= exp−exp |
|
0,34 |
= 0,9967. Полученное при R(S) = 0,9967 значение даль- |
|||||||||
|
|
|
|
|
|
А |
|
|
|
|
||
ности отказа βs |
= 2,71 рассматривается как величина снеговой нагрузки при ус- |
|||||||||||
ловии её нормального распределения, т.е. принимается S = 2,71 кПа. Уточняется |
||||||||||||
значение β = (βs2 + βn2)1/2 = (2,712 + 2,42)1/2 = 3,62 или S |
= 3,62 кПа. Далее опять |
|||||||||||
|
|
|
|
|
|
б |
|
|
по нормальному закону, |
|||
определяют дальность отказа величин, распределённыхД |
||||||||||||
βn = (9,31 – 3,75 - 3,62)/0,847 = 2,29 и β = (2,712 |
+ 2,292)1/2 = 3,55. Процесс итера- |
|||||||||||
|
|
|
|
|
и |
|
|
|
|
|
β = 3,55. |
|
ции заканчивается, так как стало известным минимальное значение |
||||||||||||
Этому значению соответствует PR = 0,9998. Как видим, приближённое значение |
||||||||||||
|
|
|
|
С |
|
|
|
|
|
|
|
|
вероятности безотказной работы несколько завышает надёжность плиты. Пример 4.2. Определ ть вероятность отказа сборной железобетонной
плиты по серии 1.465.1-7/84 в плоском совмещённом покрытии здания, запроектированного до 2003 г., при действии постоянной и снеговой нагрузок и следующих исходных данных: район строительства г. Омск; класс арматурной стали А 600; ширина плиты bпл = 1,5 м, толщина полки hп = 3 см, толщина рёбер b = 16 см; высота плиты h = 30 см; расстояние от центра тяжести арматуры As до крайнего растянутого волокна a = 3 см.
Структура покрытия: плита, пароизоляция из слоя рубероида, утеплитель толщиной 20 см из минераловатных плит плотностью 200 кг/м3, керамзитовая засыпка для разуклонки кровли средней толщиной 10 см из керамзита плотностью 600 кг/м3 и четырёхслойная рубероидная кровля.
Как и в предыдущем примере, рассматриваем снеговую нагрузку в районе г. Омска. Среднее значение ежегодных максимумов составляет S1 = 0,7 кПа, среднее максимальное значение 25-летних периодов S25 = 1,8 МПа и стандартное отклонение sS = 0,44 кПа. Эти параметры используются при аппроксимации распределения снеговой нагрузки нормальным законом.
197
Постоянную нагрузку считаем распределённой по нормальному закону с
функцией |
распределения R(q)= Ф[(g − g )/ sg ], где |
g − среднее значение; |
|
~ |
|
sg − стандарт суммарной постоянной нагрузки.
Сбор постоянных нагрузок на покрытие
Вид нагрузки |
gni, кПа |
γf |
gi, кПа |
1.Вес плит покрытия |
1,7 |
1,1 |
1,87 |
2.Вес пяти слоёв рубероида 0,05 5 |
0,25 |
1,3 |
0,325 |
3.Вес утеплителя 200 0,2/100 |
0,4 |
1,3 |
0,52 |
4.Вес керамзита 600 0,1/100 |
0,6 |
1,3 |
0,78 |
Итого |
2,95 |
|
3,495 |
Принимаем g = ∑gni = 2,95 кПа. Согласно разделу 4, определяем весовые коэффициенты α1 = 1,7/2,95 = 0,58; α2 = 0,25/2,95 = 0,08; α3 = 0,4/2,95 = 0,14;
α4 = 0,6/2,95 = 0,2. В зависимости от коэффициента надёжности по нагрузке |
|||
принимаем коэффициенты вариации по табл. 2.6. Для плит покрытия v1 |
= 0,033, |
||
для прочих нагрузок vi = 0,1. По формуле (2.9) вычисляем коэффициент вариа- |
|||
|
Д |
|
|
ции для постоянной нагрузки vg = 0,032 и стандартное отклонение sg = 0,095 кПа. |
|||
По суммарной нормативной нагрузке |
(без учёта веса |
плиты) |
|
|
А |
0 |
|
gn = (2,95 – 1,7) + 0,7 = 1,95 кПа принимается плитаИ2ПГ6-2АIV, армированная |
|||
двумя стержнями 12 A 600 (As = 2,26 см2). Класс бетона по прочности на сжа- |
|||
тие В15. |
б b |
|
|
Суммарная расчётная нагрузка составляет g0 |
= 0,7∙1,4 + 3,495 = 4,475 кПа. |
||
Погонная расчётная нагрузка g = 4,475 1,5 = 6,71 кН/м. Расчётный изгибающий |
||||||||||
момент при |
|
и |
|
и |
пролёте плиты l |
= |
5,9 |
м |
||
|
балочной расчётной схеме |
|||||||||
MQ = gl02/8 = 29,21 кН м. |
|
|
|
|
|
|
|
|
||
|
|
С |
R |
= |
8,5 |
МПа; |
арматурной |
стали |
||
Расчётные сопрот влен я: бетона |
||||||||||
Rs = 510 МПа. |
|
|
|
|
|
|
|
|
|
|
При h0 |
= h − a = 27 см проверяем несущую способность плиты из расчёта |
|||||||||
по предельному состоянию. |
|
|
|
|
|
|
|
|
||
Проверяем положение нижней |
границы |
сжатой |
зоны. |
Так |
как |
|||||
Rbbf′hf′ = 38,25 < RsAs = 115,26 кН, то граница сжатой зоны проходит в полке. Определяем коэффициенты ξ = RsAs/Rbbf′h0 = 0,033 и αm = 0,033. Расчётная несущая способность плиты по прочности нормальных сечений
MR = αmRbbf′h02 = 30,67 кН м > 29,21 кН м.
По табл. 3.5 при vb = 0,135 определяем характеристики прочности бетона: Rb = 14,08 МПа; sb = 1,9 МПа. По табл. 3.1 определяем характеристики прочности арматурной стали: Rs = 690 МПа, vs = 0,09 и ss = 62 МПа. Коэффициент ар-
мирования µ = As/bh0 = 0,0052 > µmin = 0,0005. |
|
|||
|
По алгоритму, изложенному в данном разделе, определяем характеристи- |
|||
ки прочности плиты: |
|
= µbRs/bf′Rb = 0,027 < ξR = 0,472; ξ1 |
= ξ vs/ vb = 0,018; |
|
ξ |
||||
βξ |
= (ξR Rb − µ Rs)/(ξRsb − µss) = 5,4; PR ≈ 1; P ≈ 0; |
ξ = ξ1 = 0,018; |
||
vR |
= vs(1 − 0,5ξ)/(1 − 0,5 ξ) = 0,09. Характеристики несущей способности пли- |
|||
198

ты MMR = RsAsh0(1 − 0,5 ξ) = 41,54 кН м и sMR = 3,74 кН м. Этим значениям несущей способности эквивалентна равномерно распределённая нагрузка
qR = 8 MR/bпл l02 = 6,36 кПа и sR = 0,57 кПа.
Надёжность плиты определяем по формулам (1.17) − (1.18). При снеговой нагрузке S = 0,7 кПа β = ( qR − S − g )/ 
 sR2 +sS2 +sg2 = (6,36 − 0,7 − 2,95)/(0,572 +
sR2 +sS2 +sg2 = (6,36 − 0,7 − 2,95)/(0,572 +
+ 0,442 + 0,0952)1/2 = 3,73, что соответствует вероятности безотказной работы PR = 0,9999. Для несущих конструкций сооружений II уровня ответственности считается достаточной надёжность PR = 0,995. При расчётной снеговой
нагрузке S = 1,8 кПа дальность отказа β = (6,36 − 1,8 − 2,95)/0,726 = 2,218, что соответствует вероятности безотказной работы PR = 0,9867 < 0,995, т.е. надёжность запроектированных плит покрытия при увеличенной снеговой нагрузке недостаточна.
Используя для анализа надёжности опытные значения С = 1,67 и vC = 0,16
(см. раздел 4.3, табл. 4.3), получим |
|
R = |
|
M R |
= 1,67 30,67 = 51,22 кН м; |
M |
C |
||||
|
|
|
|
|
И |
qR = 7,85 кПа и sR = 0,16 7,85 = 1,255 кПа. Надёжность плиты на проектную на- |
|||||
грузку уменьшается PR = 0,9996 (β = 3,333), а с увеличением снеговой нагрузки
становится недостаточной PR = 0,993 < 0,995 (β = 2,446).
Уточним вероятность безотказной работы плиты, полученную в послед-
нем варианте расчёта методом поиска минимального значения β последователь- |
|||||
А |
|
|
снеговой |
нагрузки |
|
ным приближением. В первом приближении значение |
|||||
S = 1,8 + 2,218 0,44 = 2,76 кПа и дальность отказа величин, распределённых по |
|||||
нормальному закону, определяется из выраженияДβ = ( q |
R |
− S − g )/ |
s2 |
+ s2 = |
|
|
n |
|
R |
g |
|
= (7,85 – 2,76 − 2,95)/1,259 = 1,7. Вероятность реализации приближённого значения S = 2,76 кПа вычисляется при u = 0,5 + 0,34ln25 = 1,59 кПа из формулы
|
1,59 − S |
= 0,9685. Полученное при R(S) = 0,9685 значение даль- |
|
R(S )= exp−exp |
|
||
|
0,34 |
б |
|
ности отказа βs |
= 1,86 рассматр вается как величина снеговой нагрузки при ус- |
||
ловии её нормального распределенияи |
, т.е. принимается S = 1,86 кПа. Уточняется |
||
значение β = (βs2С+ βn2)1/2 = (1,862 + 1,72)1/2 = 2,52 или S = 2,52 кПа. Затем опять определяется дальность отказа величин, распределённых по нормальному зако-
ну, βn = (7,85 – 2,52 − 2,95)/1,259 = 1,89 и β = (1,862 + 1,892)1/2 = 2,65 > 2.52. Уточ-
няем еще раз βn = (7,85 – 2,65 − 2,95)/1,259 = 1,89 и β = (1,862 + 1,892)1/2 = 2,65.
Процесс итерации заканчивается, так как стало известным минимальное значение β = 2,52. Этому значению соответствует PR = 0,9949 < 0,995. Как видим, приближённое значение вероятности безотказной работы незначительно отличается от уточнённого значения.
199
