
- •ВВЕДЕНИЕ
- •1. РАСЧЕТ КАК ИНСТРУМЕНТ ОБЕСПЕЧЕНИЯ НАДЕЖНОСТИ КОНСТРУКЦИЙ
- •1.1. Изменчивость расчётных параметров
- •1.2. Применение теории вероятностей для учета изменчивости
- •1.3. Особенности нормального закона распределения
- •1.4. Параметры метода расчёта по допускаемым напряжениям
- •1.6. Вероятностная зависимость параметров исходных данных
- •1.7. Метод расчёта по разрушающим нагрузкам и условный коэффициент запаса
- •1.8. Расчётные параметры метода предельных состояний
- •1.9. Совершенствование метода предельных состояний
- •1.10. Учёт фактора времени
- •2.3. Постоянные нагрузки
- •2.4. Полезные нагрузки на перекрытия
- •2.5. Снеговые нагрузки
- •2.6. Ветровые нагрузки
- •2.7. Температурные климатические воздействия
- •2.8. Крановые нагрузки
- •2.9. Аварийные ударные воздействия
- •2.11. Сочетания нагрузок
- •3. ИЗМЕНЧИВОСТЬ СВОЙСТВ СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ
- •3.1. Основные положения
- •3.2. Строительные стали
- •3.3. Бетоны
- •3.4. Строительные растворы
- •3.5. Кирпич и каменная кладка
- •3.6. Древесина
- •3.7. Грунты
- •4. ЗАДАЧИ РАСЧЁТА КОНСТРУКЦИЙ НА НАДЁЖНОСТЬ
- •4.1. О надёжности ограждающих конструкций при расчёте на теплопередачу
- •4.2. Вероятностная оценка прочности железобетонных элементов по нормальным сечениям при изгибе
- •4.3. Изменчивость несущей способности изгибаемой конструкции
- •4.4. Неопределенность расчетных моделей конструкций
- •Библиографический список

2.7.Температурные климатические воздействия
Вконструкциях зданий и сооружений, подвергающихся воздействию изменяющейся во времени температуры наружного воздуха, возникают температурные усилия и деформации. Несмотря на то, что температура наружного воздуха имеет случайный характер, действующие нормы проектирования задают расчётные показатели температуры в детерминированном виде с неопределённой зависимостью от времени в процессе многолетнего режима эксплуатации зданий. Представление температурных воздействий в вероятностном виде позволяет не только более точно задать расчётные параметры, но и оце-
нить надёжность и долговечность конструкций, в которых температурные усилия и деформации также имеют Ислучайный характер, как и сами температуры.
Согласно нормам, основным видомДтемпературных климатических воздействий на несущие конструкции являются изменения сред-
ней по сечению элементов температуры в тёплое t и холодное t время года по отношению к начальнымАтемпературамw t0w и t0c замыканияc конструкции в законченную систему. В дальнейшем будем рассматривать температуру t в общембвиде без привязки к конкретному сезону.
Для учёта случайнойиизменчивости температуры наружного воздуха во времени её представляют в виде случайного процесса. В наиболее общемСслучае этот процесс характеризуется суммой случайных амплитуд пер од ческ х колебаний с периодом, равным одному году, периодических колебаний с периодом, равным одним суткам, и непериодических колебаний на интервалах времени более суток. Согласно стандарту [18], для общетехнических целей характер изменения температуры во времени оценивается случайным процессом.
t (τ)= t (τ)+ψ(τ), |
(2.59) |
~ ~
где t(τ) и ψ~(τ) − средняя температура и случайная составляющая температуры с математическим ожиданием, равным нулю, соответст-
вующие времени τ, °С.
Для технических целей наиболее точной моделью является непрерывный процесс почасовых изменений температуры. Применительно к расчётам конструктивных систем наиболее существенными считаются изменения во времени τ среднесуточной температуры на-
109
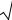
ружного воздуха, которые в дальнейшем рассматриваются как случайные функции и обозначаются ~t (τ).
Ежегодные реализации частных значений среднесуточных температур t можно считать независимыми из-за большого интервала времени между ними (365 суток). Функция ψ~(τ) как сумма независи-
мых случайных величин, из которых каждая может быть распределена по любому закону при увеличении числа этих величин в многолетнем процессе, стремится к нормальному закону распределения с плотностью
|
|
|
|
~ |
|
|
2 |
|
|
||
|
|
1 |
|
−t |
|
|
|||||
p |
(τ)= |
|
|
exp − [t |
|
(τ)] |
, |
(2.60) |
|||
|
|
|
|
|
|
|
|||||
t |
|
st (τ) 2π |
|
|
2st2 |
(τ) |
|
|
|||
|
|
|
|
|
|
||||||
где t(τ) и st(τ) − математическое ожидание и стандарт случайной ве- |
|||
|
|
|
И |
личины среднесуточной температуры t в момент времени τ. |
|||
|
|
~ |
|
|
Плотность (2.60) получена из одномерного закона распределе- |
||
ния |
|
Д |
|
t и является основной вероятностной характеристикой процесса |
|||
|
~ |
|
|
многолетних реализаций. При известных t (τ) и st(τ) подобная функция позволяет оценить вероятность, например, расчётного значения t
в частный момент времени τ илиАопределить область значений t с за-
при интервале времени, стремящемся к нулю. Строго говоря, основ-
данной обеспеченностью. При этом требуется учёт взаимного влияния частных значений t, которыеб, как правило, корреляционно связа-
ными характерист ками случайной функции являются математиче-
ны между собой в годовом ходе температур. Корреляционная связь тем больше, чем ближе частные значения, и считается максимальной
ское ожидание и корреляционная функция, которая только в частном
случае обращается в дисперсию st2(τ). Поэтому для решения постав- |
|
ленной задачи недостаточно одной зависимости (2.60). |
|
Данные справочникаС |
по климату [27] о повторяемости среднесу- |
точной температуры воздуха в отдельные месяцы года дают возможность приближённо оценить плотность распределения (2.60), если считать ежемесячные процессы среднесуточных температур стационарными. Основными условиями стационарности часто считают постоянные величины математических ожиданий и дисперсий (стандартов). Первое условие выполняется при переходе от обычной случайной функции к центрированной, для которой математическое ожидание постоянно, так как тождественно равно нулю. Выражение (2.60) для плотности примет вид
110

|
1 |
|
|
|
~ |
2 |
|
|
pt (τ)= |
|
|
t |
|
|
|||
|
|
|
exp − |
|
|
. |
(2.61) |
|
|
|
|
|
|
||||
st (τ) 2π |
2st2 |
|
||||||
|
|
|
(τ) |
|
||||
В ГОСТе [18] принято также и второе условие постоянства стандарта среднесуточных температур на протяжении всего годового хода температур (по нашей оценке, для г. Омска эта величина равна
6,6 °С). В действительности изменчивость среднесуточной температуры воздуха в зимние месяцы больше летней почти в два раза. Более общим условием стационарности является зависимость корреляцион-
ной функции только от разности промежутка времени ∆τ между двумя реализациями [11].
На практике вместо корреляционной функции kt(τ) часто поль-
зуются нормированной корреляционной функцией ρt(∆τ) = kt(τ)/st2(τ), с помощью которой можно оценить максимальное время корреляции
τk, т.е. интервал времени, за которым две смежных реализации t(τ1) и t(τ2) можно считать практически независимыми. В работе [43] соотношение τk ≤ ∆τ оценивают из условия |ρt(∆τ)| ≤ 0,05. Обычно корре-
ляционные функции дифференцируемых случайных стационарных |
|||||
|
|
|
|
И |
|
функций аппроксимируют выражением [55] |
|
||||
kt (τ)= st2 exp(−λτ2 ), |
(2.62) |
||||
|
|
Д |
|
||
где λ = 1/∆τ − частота реализаций в интервале времени ∆τ. |
|
||||
Применительно к нашему случаю при ρt(∆τ) = exp(−λτ2) = 0,05 |
|||||
имеем ln(0,05) = − 3 = − λτ2 |
А |
|
|
||
τ = |
3∆τ. Если оперировать ежесуточ- |
||||
ными реализациями среднесуточныхб |
температур, то ∆τ = 1 и время |
||||
и |
|
|
|
|
|
С |
|
|
|
|
|
корреляции τk более суток, т.е. каждая реализация зависит от смежных; если использовать среднемесячные реализации, то ∆τ = 30 и время корреляции τk менее 10 cуток, что позволяет считать выбранные реализации независимыми. Для ежегодных реализаций τk = 33 суток.
Так как корреляционная функция (2.62) дважды дифференцируема (имеет точки перегиба), то и случайная стационарная функция ~t (τ) должна быть дифференцируемой или условно дифференцируемой по времени. Производную дифференцируемой случайной функции, которая является также случайной функцией d~t (τ)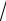 dτ = v~t (τ),
dτ = v~t (τ),
можно трактовать как скорость изменения среднесуточной температуры ~t . Оценить производную v~t (τ) можно по данным о междусу-
точной изменчивости, приведённым в справочниках по климату [27].
111
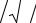
Из табл. 2.27 видно, что при среднегодовом значении vt = 3 °С
изменчивость vt(τ) в зимние месяцы в 1, 5 − 2 раза больше, чем в летние месяцы. Аналогичное соотношение имеют опытные значения st.
Таблица 2.27
Осреднённые значения междусуточной изменчивости vt и стандартного
|
|
отклонения st (°С) температуры воздуха в г. Омске по месяцам |
|
||||||||||||
I |
|
II |
|
III |
IV |
V |
VI |
VII |
VIII |
|
IX |
|
X |
XI |
XII |
4,1 |
|
3,9 |
|
3,4 |
2,3 |
3,1 |
2,6 |
1,9 |
2,1 |
|
2,3 |
|
2,3 |
3,7 |
4,4 |
7,8 |
|
7,9 |
|
6,9 |
6,3 |
6,2 |
4,9 |
4,0 |
4,0 |
|
4,8 |
|
5,0 |
8,2 |
8,7 |
|
При нормальном законе распределения |
~ |
|
|
|
|
|||||||||
|
t (τ) распределение про- |
||||||||||||||
изводной |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
||
vt (τ) также является нормальным и независимым от распре- |
|||||||||||||||
деления ~t |
(τ). Так как математическое ожидание производной от слу- |
||||||||||||||
|
|
|
|
|
|
|
|
|
И |
|
|
|
|||
чайной функции равно производной от её математического ожидания,
то для стационарной функции при t(τ) = const получим vt(τ) = 0. Для
практических расчётов иногда нужно знать зависимость условного
математического ожидания производной, определяемого из наиболее
опасных значений изменчивости среднесуточных температур, от
стандарта производной sv(τ). В работе [12] эта задача сведена к нахо- |
||||
|
|
|
|
Д |
ждению математического ожидания модуля случайной величины, |
||||
распределённой по нормальному закону. Полученное решение |
||||
vt (τ)= sv (τ) |
|
≈ 0,8sv(τ) являетсяАоценкой стандарта производной в |
||
2 π |
||||
отдельные месяцы года. |
б |
|
||
|
|
|
|
|
С точки зрен я надёжности оценку температурного воздействия |
||||
туры тёплого илиСхолодного времени года с учётом фактора времени. Наиболее интересны задачи определения расчётного уровня температуры или расчётного времени до первого выброса.
следует обеспечить вероятностными характеристиками выхода (вы- |
||
броса) процесса |
~ |
и |
t (τ) за определённый (расчётный) уровень темпера- |
||
Найдём вероятность пересечения случайным процессом расчётного уровня среднесуточной температуры t в течение бесконечно ма-
лого промежутка времени dτ. Полагая скорость изменения случайной
|
|
~ |
|
|
|
|
функции vt (τ) постоянной в течение времени dτ, запишем условие |
||||||
пересечения функцией t (τ) |
уровня t |
(условие выброса) |
в виде |
|||
|
|
~ |
|
|
|
|
t |
|
~ |
~ |
|
~ |
> 0. Веро- |
(τ) < t; t (τ) + vt (τ)dτ > t или t − vt (τ)dτ < t (τ) < t при vt (τ) |
||||||
~ |
~ |
|
|
~ |
|
|
ятность этого события равна:
112

P = ∞∫ ∫t p(t,v)dtdv, |
(2.63) |
|
0 t−vdτ |
t (τ) |
и |
где p(t, v) − совместная плотность распределения функций |
||
|
~ |
|
v~t (τ).
Учитывая, что пределы интегрирования во внутреннем интеграле отличаются на бесконечно малую величину, выражение (2.63) представим в виде
P = dτ∞∫ p(t,v)vdv. |
(2.64) |
0 |
|
Поскольку вероятность выброса в течение бесконечно малого интервала времени dτ пропорциональна величине этого интервала,
используют понятие потока выбросов в единицу времени P/dτ. Путём |
||
0 |
И |
получают |
интегрирования потока выбросов |
на отрезке времени τ |
|
среднее число или частоту выбросов n. Для стационарных процессов |
|||
частота выбросов равна: |
|
Д |
|
|
|
|
|
n = τ∞∫ p(t,v)vdv . |
(2.65) |
||
|
А |
|
|
Плотность совместного распределения независимых случайных |
|||
функций определяют из известного условия теории вероятностей: |
|||
p(t,v) |
= p(t)p(v). |
(2.66) |
|
и |
|
|
∫ p(v)vdv |
Подставляя (2.66) в (2.65) |
и учитывая, что интеграл |
||
представляет собой математбческое ожидание положительной межсу-
точной изменчивости температуры vt, а время положительных выбросов в два раза меньше общего отрезка времени, получим
|
|
|
n = |
vt p(t)τ |
. |
(2.67) |
|||
|
|
|
|
|
|
|
|||
|
|
|
2 |
|
|
|
|||
|
Отсюда получим выражение для вероятностной оценки процес- |
||||||||
са: |
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
2n |
|
|
|
|
|
|
|
p(t)= |
. |
(2.68) |
||||
|
|
|
|
||||||
|
|
|
|
|
|
τvt |
|
||
|
Применим для расчётного значения среднесуточной температу- |
||||||||
ры выражение с использованием нормируемого параметра z: |
|
||||||||
|
|
|
t = t |
− zst . |
(2.69) |
||||
|
Подставим z = t |
−t в формулу (2.60): |
|
||||||
|
|
st |
|
|
|
|
|
|
|
113
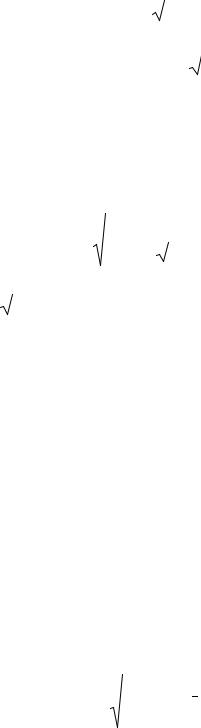
|
|
|
|
z |
2 |
|
|
||
|
|
− |
|
|
|
|
|||
|
|
|
|
|
|||||
|
exp |
2 |
|
|
|||||
p(t)= |
|
|
|
|
. |
(2.70) |
|||
st |
|
|
|
|
|
|
|||
|
2π |
||||||||
|
|
|
|
|
|||||
Из сопоставления (2.70) с (2.68) получим
|
|
|
2 |
|
|
2nst |
|
|
|
|
z |
|
2π |
|
|
||||
|
− |
|
|
= |
. |
(2.71) |
|||
|
|
|
|||||||
exp |
2 |
|
τvt |
|
|||||
|
|
|
|
|
|
|
|||
Отсюда можно вычислить значение квантили z переменной ~t (τ)
для любого промежутка времени τ, по которому определяется расчётное значение (2.69) среднесуточной температуры наружного воздуха
при n = 1:
|
|
|
|
|
|
τv |
|
|
|
|
|
|
||
|
|
|
z = |
|
2ln |
|
|
t |
|
s . |
(2.72) |
|||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
2 |
|
2π |
t |
|
|
|
|||
Из этого выражения можно определить минимальное значение |
||||||||||||||
периода τmin = |
2st 2π |
, |
характеризуемое условием корреляции част- |
|||||||||||
|
||||||||||||||
|
vt |
|
|
|
|
|
|
|
|
|
И |
|
||
ных значений t. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Подобный подход |
к |
оценке экстремальных |
среднесуточных |
|||||||||||
температур воздуха реализован в |
Д |
|
||||||||||||
работе [7]. Поскольку основная |
||||||||||||||
часть выбросов за тёплоеб(холодноеА) полугодие происходит в трёхмесячном летнем (зимнеми) сезоне, допустимо вычислять частоту выбросов по осреднённым значен ям статистических характеристик на этих интервалах. ТакаяСмодель для зоны с умеренно-холодным климатом требует расчётной проверки.
В табл. 2.28 приведены результаты вычисления расчётных среднесуточных температур с различными периодами вероятных выбросов в тёплое время года для условий г. Омска.
Осреднённые значения стандартных отклонений определены из опытных данных о повторяемости m среднесуточной температуры по месяцам за 30-летний период [27] наблюдений расчётом по формуле
s = |
|
|
|
|
∑t2m −t |
2 . |
(2.73) |
||
t ∑m
Для всех вариантов расчёта τmin = 10 суток, что соответствует условию корреляции среднемесячных значений. Результаты расчёта соответствуют опытным данным: за почти 90-летний период наблюдений наибольшее значение среднесуточной температуры составило
+32,8 °С (1.VII.1900). В наибольшей степени этому условию удовле-
114

творяет вариант с теплым двухмесячным периодом (июнь + июль), результаты расчета по которому рекомендуются для использования в практических целях.
Таблица 2.28
Положительные среднесуточные температуры (°С ) для расчёта
конструкций на температурные воздействия в условиях г. Омска и z - коэффициенты обеспеченности расчётного значения
Длительность тёплого пе- |
Длительность температурного воздействия T, |
||||||||||||
риода (месяцы) и |
|
|
|
|
|
лет |
|
|
|
||||
расчётные параметры |
150 |
|
100 |
|
50 |
25 |
10 |
5 |
1 |
||||
VII (τ = 30Т суток; |
|
|
32,3 |
|
31,8 |
|
30,9 |
30,0 |
28,7 |
27,6 |
24,2 |
||
t = 18,3 °С; |
st |
= 4,0 °С; |
|
3,49 |
|
3,37 |
|
3,16 |
2,93 |
2,60 |
2,32 |
1,47 |
|
vt = 1,9 °С) |
|
|
|
|
|
|
|
|
|
|
|
|
|
VII+VIII (τ |
= |
62Т |
суток; |
|
31,9 |
|
31,4 |
|
30,7 |
29,8 |
28,6 |
27,6 |
24,7 |
t = 17,1 °С; |
st = |
4,0 °С; |
|
3,70 |
|
3,58 |
|
3,39 |
3,17 |
2,87 |
2,62 |
1,91 |
|
vt = 2,0 °С) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
33,4 |
|
Д |
31,6 |
30,2 |
29,1 |
25,9 |
VI+VII (τ |
= |
61Т |
суток; |
|
33,9 |
|
|
32,5 |
|||||
t = 17,5 °С; |
st = |
4,5 °С; |
|
3,70 |
|
3,58 |
|
3,39 |
3,17 |
2,87 |
2,62 |
1,91 |
|
vt = 2,3 °С) |
|
|
|
|
|
|
|
|
|
И |
|
|
|
VI+VII+VIII(τ = 92Т суток; |
|
33,3 |
|
32,8 |
|
32,0 |
31,1 |
29,9 |
28,8 |
26,0 |
|||
|
|
|
|
|
б |
|
|
|
|
|
|
||
t = 16,9 °С; |
st = |
4,3 °С; |
|
3,81 |
3,70 |
|
3,51 |
3,30 |
3,01 |
2,77 |
2,12 |
||
vt = 2,2 °С) |
|
|
|
|
|
|
|
|
|
|
|
|
|
VI+VII+VIII+IX |
|
|
32,5 |
32,0 |
|
31,2 |
30,3 |
29,0 |
28,0 |
25,2 |
|||
(τ =122Т суток; t = 15,4 °С; |
|
3,88 |
А3,77 |
3,58 |
3,38 |
3,10 |
2.87 |
2.24 |
|||||
st = 4,4 °С; vt = 2,2 °С) |
|
|
|
|
|
|
|
|
|
|
|||
V+VI+VII+VIII+IX |
|
|
33,3 |
32,8 |
|
31,9 |
31,0 |
29,6 |
28,5 |
25,6 |
|||
(τ = 153Т суток; t = 14,4 ° ; |
|
3,93 |
3,83 |
|
3,64 |
3,45 |
3,17 |
2,94 |
2,33 |
||||
st = 4,8 °С; vt = 2,4 ° |
) и |
|
|
|
|
|
|
|
|
||||
V+VI+VII+VIII+IX+X |
31,3 |
30,8 |
|
29,9 |
29,0 |
27,7 |
26,6 |
23,8 |
|||||
(τ = 184Т cуток; t = 14,4 °С; |
3,98 |
3,88 |
|
3,69 |
3,50 |
3,23 |
3,01 |
2,41 |
|||||
st = 4,8 °С; vt = 2,4С°С) |
|
|
|
|
|
|
|
|
|
||||
IV+V+VI+VII+VIII+IX+X |
30,7 |
30,2 |
|
29,3 |
28,4 |
27,0 |
25,9 |
23,0 |
|||||
(τ = 214Т cуток; t = 14,4 °С; |
4,01 |
3,91 |
|
3,72 |
3,53 |
3,26 |
3,04 |
2,46 |
|||||
st = 5,0 °С; vt = 2,4 °С) |
|
|
|
|
|
|
|
|
|
||||
Рекомендуемое нормами расчётное значение среднесуточной
температуры +37,4 °С с учётом коэффициента надёжности 1,1 значительно превышает прогнозируемое любыми моделями тёплого периода при длительности воздействия до 150 лет. Анализ показывает, что при уменьшении продолжительности тёплого периода снижается обеспеченность, которая соответствует вероятности выброса значе-
115

ний среднесуточной температуры за уровень расчётного значения и зависит от длительности тёплого периода и воздействия в целом.
Так как основным видом температурных климатических воздействий на конструктивные системы являются приращения среднесу-
точных температур ∆t = t − t0 по отношению к начальным температурам t0 замыкания конструкции в законченную систему, рассмотрим
эти приращения как случайную функцию ∆~t = ~t − ~t0 .
В соответствии с подходом, принятым при разработке норм [60], начальные температуры конструкций t0w иt0c оцениваются осреднением по времени соответствующих полугодовых гармоник среднесу-
точной температуры со случайной амплитудой A[54]: |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
2A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
= t0 ± |
|
|
|
|
|
|
|
|
|
|
|
|
(2.74) |
||||||||||||
|
|
|
|
|
t0 |
|
π . |
|
|
|
|
|
И |
|||||||||||||||||
При оценках среднегодовой температуры t0 |
= ( tVII |
+ tI )/2 и по- |
||||||||||||||||||||||||||||
лугодовой амплитуды А = ( tVII |
− tI |
|
)/2 средние значения начальных |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
|
|
||||||||||||
температур определяются по формулам: для лета t0w = (π + 2) tVII /2π+ |
||||||||||||||||||||||||||||||
+ (π − 2) tI /2π ≈ 0,8 tVII |
+ 0,2 tI |
и зимы t0c ≈ |
0,2 tVII |
+ 0,8 tI. Для |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
оценки среднеквадратического отклонения В. . Райзером принято |
||||||||||||||||||||||||||||||
выражение s |
= s2 |
+ s2 |
|
π. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
VII |
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
~ |
|
Исходя из предположения независимости t |
и t0 , получены фор- |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
мулы для определения основных вероятностных характеристик ∆t : |
||||||||||||||||||||||||||||||
|
|
|
|
∆tw = tw − t0c; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
∆t |
|
= t |
c |
− t |
0w |
; |
|
|
|
|
|
|
|
|
(2.75) |
||||||||||
|
|
|
бc |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
sI2 |
|
|
|
|
|
|||
|
|
s |
|
= |
|
1 |
+ |
|
|
|
|
s |
VII |
+ |
|
|
|
|
; |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
иw |
|
|
|
|
|
π2 |
|
|
|
|
|
|
|
|
π2 |
|
|
|
|
|
|||||||||
|
Сsc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
s2 |
|
|
|
|
|
|
|||||||||
|
= |
|
1 |
+ |
|
|
|
sI + |
|
|
|
VII |
. |
|
|
|
||||||||||||||
|
|
|
π2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π2 |
|
|
|
|
|
||||||
Для г. Омска получены следующие значения вероятностных ха-
рактеристик: t0c = − 11,7 °С; sc = 5,3 °С. По данным табл. 2.28 и этим параметрам можно нормировать климатические температурные воздействия для расчёта по предельному состоянию или выполнить вероятностный расчёт с учётом временного фактора.
Так как случайные величины температурных воздействий и прочностных характеристик конструкций подчиняются закону нормального распределения, для оценки надёжности удобно применить
116

метод двух моментов. Метод заключается в определении вероятности неразрушения через интеграл вероятностей P = Ф(β).
Характеристика безопасности β определяется по формуле
β = M − Mt , (2.76)
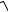 sM2 + sT2
sM2 + sT2
где M − среднее значение несущей способности конструктивного элемента; Mt − среднее значение усилия от температурного воздейст-
вия; sM − стандартное отклонение несущей способности; sT − стандартное отклонение температурного усилия.
Покажем на примере, как работает изложенная методика расчёта. Определённая по СНиП 2.01.07−85* расчётная температура для
прочностных расчётов составляет ∆tw = 50,6 °С. Расчётное значение несущей способности элемента принято по температурному усилию
M = Mt = |
1,32 кН м, определённому из статического расчёта. Обеспе- |
|
ченность |
расчётной величины M |
Д |
характеризуется изменчивостью |
||
прочностных свойств арматуры, исходя из чего определены средняя
|
А |
|
величина M |
= 1,63 кН м и стандартное отклонениеИsM |
= 0,13 кН м. |
Так как в нормах отсутствуют указания по изменчивости температур- |
||
ных воздействий, средняя величина температурного усилия принята равной нормативному значению Mt = 1,32/1,1 = 1,2 кН м, а стандартное отклонение определено в соответствии с sc = 5,3 °С из пропорции
sT = 1,32 5,3/50,6 = 0,14 кН м. |
выполнен по |
формуле |
(2.76) |
и дан- |
|||||||||||
Вероятностный расчёт |
|||||||||||||||
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
||
ным, полученным в этой работе. Результаты расчёта приведены в |
|||||||||||||||
табл. 2.29. |
|
и |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Результаты расчёта на надёжность |
|
|
Таблица 2.29 |
|||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
Пара- |
Нормы |
10 |
1 |
|
5 |
10 |
|
25 |
|
50 |
|
100 |
|
150 |
|
метры |
|
|
суток |
год |
|
лет |
лет |
|
лет |
|
лет |
|
лет |
|
лет |
∆tw, °С |
|
46 |
29,2 |
37,6 |
|
40,8 |
41,9 |
|
43,3 |
|
44,2 |
|
45,1 |
|
45,6 |
β |
|
2,25 |
4,14 |
3,40 |
|
2,98 |
2,83 |
|
2,62 |
|
2,51 |
|
2,36 |
|
2,22 |
P |
|
0,988 |
0,999 |
0,999 |
|
0,999 |
0,998 |
|
0,996 |
|
0,994 |
|
0,990 |
|
0,987 |
Из сопоставления результатов расчёта видно, что надёжность конструкции, запроектированной по нормам, соответствует длительному сроку температурного воздействия. Вероятность неразрушения конструкции при этом не отвечает общепризнанным требованиям
117
