ния, которые могут быть детерминированными и случайными [4]. Такой подход применён при вероятностном моделировании технологических нагрузок на перекрытия от оборудования [54]. Наиболее удобной с точки зрения проектирования формой учёта этой неравномерности является переход к эквивалентным равномерно распределённым нагрузкам. Такая нагрузка создаёт в рассматриваемом элементе усилия и деформации, равные усилиям и деформациям от фактической нагрузки. Принимаемые расчётные значения эквивалентных нагрузок должны обеспечить несущую способность и жёсткость элементов и зависят от критерия, положенного в основу определения нагрузок. По этой причине эквивалентные нагрузки для расчёта разных элементов перекрытия могут различаться. Это различие определяется

разницей в приведении действительной нагрузки на перекрытие к эквивалентной. При этом возможно применениеИразличных расчётных

схем, однако для выявления статистического характера поведения на-

грузки на перекрытия рассматриваютсяДтолько свободно опёртые не-

сущие элементы. Интенсивность эквивалентных нагрузок для различных несущих элементов можно считать случайной величиной с определёнными функциями распределенияА[9].

С целью определения наибольших усилий (деформаций) в статически неопределимых системахбперекрытий, чувствительных к неравномерным загружениям, могут чередоваться участки (пролёты) с временной нагрузкойии ез неё. Надо только уметь правильно оценить вероятность различных загружений.

С2.5. Снеговые нагрузки

При проектировании конструкций в качестве снеговой нагрузки принимают максимальный вес снега на единицу горизонтальной проекции площади покрытия сооружения. Расчётная модель снеговой нагрузки не требует особенно тонкого учёта временной и пространственной изменчивости, так как она оказывает на конструкцию лишь статическое воздействие. Поэтому в отдельных частях покрытий эта

нагрузка умножается на коэффициенты се, сt и µ, учитывающие уклон кровли, таяние в результате тепловыделений здания, ветровой перенос снега и повышенное накопление его в «снеговых мешках». По ре-

80

зультатам многолетних наблюдений, образования снегового покрова в СНиП 2.01.07–85* «Нагрузки и воздействия» приведены значения этих коэффициентов для различных типов покрытий в зависимости от скорости ветра и теплового режима сооружения.

Нормативное значение снеговой нагрузки при расчёте по методу предельных состояний определяется по формуле

Территория страны по значениям расчётной снеговой нагрузки Sg на горизонтальной поверхности земли делится на 8 снеговых рай-

онов (I – VIII) (табл. 2.13).

В качестве расчётного веса снеговогоДИпокрова принимается превышаемый в среднем один раз в 25 лет ежегодный максимум, т.е. средний максимум за 25-летний период Sq = S25, определяемый на основе данных маршрутных снегосъёмок о запасах воды на защищённых от прямого воздействия ветра участках (в лесу под кронами деревьев или на лесных полянах) за период не менее 20 лет. В некото-

рых районах страны из-за недостаткаАстатистических данных значение Sq до сих пор не установлено. При существенном отличии мест-

по первой группеСпредельных состояний, определяется умножением нормативного значения на коэффициент надежности γf = 1,4.

До 1.07.2003 г. районирование территории страны осуществлялось по средним значениям веса снегового покрова ежегодных максимумов Sg = S1, которые принимали в качестве нормативной нагруз-

ки (табл. 2.14).

Количество и границы районов были иными, поэтому из простого сопоставления данных табл. 2.13 и 2.14 можно сделать только выводы о серьёзном увеличении снеговой нагрузки при расчёте строительных конструкций.

81

Коэффициенты се, сt и µ определяются по результатам натурных наблюдений на покрытиях различной формы.

Вумеренно-тёплых районах снеговую нагрузку относят к кратковременной, так как в промежутках между снегопадами снег успевает растаять и его накопление практически исключается.

Вгорных и северных районах происходит накопление снега в течение зимы, т.е. достаточно длительного времени, поэтому часть снеговой нагрузки относят к длительно действующим нагрузкам. Од-

нако и в этих районах, по мнению А.Р. Ржаницына, в ряде случаев опасна нагрузка не от накопленного за зимуИснега, а сразу после обильного снегопада [55]. В этот период высока вероятность образования «снеговых мешков» и заносовД, так как снег выпадает при постоянном направлении ветра. Кроме этого, свежевыпавший снег не успевает быстро растаять и приАрыхлой структуре не включается в совместную работу с конструкцией.

Для учёта влияния длительности нагружения на процессы ползучести в конструкциях нормамибвыделена часть снеговой нагрузки с пониженным нормативнымизначением, которая отнесена к временной длительной нагрузке. Более точно пониженные значения определяют-

ся из совместного анал за процессов нагружения и деформирования. При этом ониСпр обретают смысл эквивалентной нагрузки, при реализации которой конструкция приобретает такое же состояние, которое реализуется при фактическом нагружении. В нормах снеговые нагрузки с пониженным нормативным значением определяются умножением полного расчётного значения на коэффициенты 0,5.

Ежегодные колебания количества снега составляют причину многолетней изменчивости снеговой нагрузки. По существу, снеговая нагрузка является случайным процессом изменения веса осадков, выпадающих в твёрдом виде в течение зимы, за вычетом их испарений и таяния. Возможной моделью случайного процесса образования снеговой нагрузки является нестационарный марковский процесс, учитывающий вероятность нахождения снега в разных состояниях [54]. Процесс называется марковским (или процессом без последствия), если для каждого момента времени вероятность любого состояния системы в будущем зависит только от состояния системы в настоя-

82

щий момент и не зависит от того, каким образом система пришла в это состояние, т.е. от предыстории. В то же время в нестационарном марковском процессе вероятность события зависит не только от продолжительности времени его действия, но и от начала отсчёта. Такой процесс имеет определённую тенденцию развития во времени. Вооб- ще-то каждый чисто случайный процесс в виде последовательности независимых наблюдений является марковским.

Статистический анализ ежедневных замеров веса снежного покрова позволяет предположить, что время пребывания процесса в определённом состоянии описывается экспоненциальным (показательным) законом. Это является признаком стационарности процесса, однако противоречий здесь нет, так как многие нестационарные процессы на известных отрезках времени и с известным приближением могут быть приняты как стационарные. При этом снеговая нагрузка в целом может быть представлена в виде профильтрованного пуассо-

максимумом. Напр мер, для Омска такой максимум приходится на конец марта.

Для расчёта на длительные сроки требуется знать максимальные снеговые нагрузки за много лет. Многолетнюю снеговую нагрузку можно получить теоретически в виде функции распределения годовых максимумов S1, корреляция между которыми практически отсутствует. Это распределение находят из статистического анализа многолетних данных о максимальной толщине снегового покрова h на

единице площади земли.

От толщины к весу снега переходят с помощью эмпирических

коэффициентов γ (плотности), т.е. S1 = γh. Если плотность снега не измеряется, то используют выражение, учитывающее зависимость плотности (кН/м3) снега от толщины покрова (м):

83

Коэффициенты α и β зависят от климатического района, для

континентального климата обычно принимается α = 1,5… 2; β = 1,5. Эти коэффициенты, толщина снегового покрова и снеговая нагрузка являются в общем случае случайными величинами или функциями.

Изменчивость γ предлагается учитывать сомножителем ερ, представляющим случайную логнормальную величину со средним значени-

ем ερ = 1 и коэффициентом вариации vε = 0,2 [72]. Логарифмически нормальное распределение применяется, когда логарифм случайной неотрицательной величины распределён нормально.

Например, при максимальной толщине h = 0,51 м в условиях

г.Омска средняя плотность снега γ = 3 – 1,5exp(− 1,5 0,51) = 2,3 кН/м3 (0,23 т/м3). В течение зимы плотность снега постепенно увеличивает-

широких пределах: от 0,02… 0,15 т/м3 (рыхлый свежевыпавший снег) до 0,3… 0,4 т/м3 и выше (мокрый снег в период снеготаяния). При увеличении толщины снегового покрова распределение плотности становится симметричным и подчиняется нормальному закону.

В работе [53] приведена эмпирическая зависимость плотности

факторов пытаютсяСучесть в аппроксимирующих функциях, тем меньше их точность.

Для определённых климатических условий величина h зависит от высоты местности H (м) над уровнем моря. Для европейских стран среднее значение ежегодной наибольшей толщины снега рекоменду-

ется определять по эмпирической зависимости h = 0,25BH, где В – коэффициент, зависящий от климатических условий и высоты местно-

сти (при H < 400 м В ≈ 1,0002). Для г. Омска, находящегося на высоте

H ≈ 100 м над уровнем моря, h = 0,255 м, что совпадает с опытными данными (табл. 2.15).

84

Изменчивость параметров се, сt и µ чрезвычайно сложна для изучения, поэтому её иногда учитывают умножением на случайную величину поправочного коэффициента [72]. В работе [76] принято

где r – коэффициент преобразования снеговой нагрузки на земле в нагрузку на крыше; k = 1,25 для прибрежных районов и k = 1,5 для рай-

Коэффициент r определяется в зависимости от детерминирован-

ных и случайных параметров, характеризующих угол наклона (до 60°)

крыши и перераспределение снега вДрезультате действия различных факторов и тепловой режим зданияА.

крыши, усредненную скорость ветра в течение недели на высоте

В.Д. Райзер на конкретном примере ограниченной выборки (статистического ряда) ежегодных максимумов оценивает возможность аппроксимации эмпирического распределения теоретическими зако-

распределение. и Кривая эмпирических распределений максимальной снеговой

нами: нормальным, логнормальным, двойным экспоненциальным и

нагрузки за один год несимметрична, причём величина S1 не может быть отрицательной и имеет высокую изменчивость. Эти факторы, по мнению А.Р. Ржаницына, исключают возможность аппроксимации эмпирического распределения нормальным законом. Эмпирическую функцию распределения снеговой нагрузки, как и ветровой, обычно аппроксимируют двойной экспоненциальной функцией распределения (распределение Гумбеля или Фишера – Типпета), которая в рабо-

Константы u и z связаны со средним значением и стандартным отклонением случайной величины. Параметры распределения (2.26)

85

зависят от местных условий и определяются из обработанных выборок годовых максимумов по формулам:

среднее квадратическое значения годовых максимумов; 0,57722 – постоянная Эйлера – Машерони.

Интегральный закон распределения Гумбеля нашёл применение в статистическом анализе не только снеговых, но и ветровых нагрузок. Он имеет ряд особенностей, отмеченных ниже, использование которых способствовало развитию вероятностных моделей климатических воздействий.

В.Д. Райзер предлагает подбирать параметры u и z по методу наименьших квадратов [51].

Считается, что коэффициент вариации ежегодных максимумов

плотность снега, определённая по формуле (2.23), составляет γ = 0,198 т/м иСснеговая нагрузка в среднем равна S1 = 50 кгс/м . При

ν = 0,45 получаем s = 22,5 кгс/м2, коэффициент z = 17,5 кгс/м2 и u = 40 кгс/м . При принятых условиях по формуле (2.28) определено, что через 25 лет возможно скопление снеговой нагрузки до 96 кгс/м2,

через 50 лет − до 108 кгс/м2, через 100 лет − до 121 кгс/м2 и через

150 лет − до 128 кгс/м2.

При ежегодной максимальной плотности снега на участках, защищённых от ветра, в г. Омскеγ = 0,28 т/м3 и среднегодовой

толщине снега h = 0,255 м S1 = 71,4 кгс/м2. Если принять v = 0,45, то получим s = 32,1 кгс/м2; z = 25 кгс/м2 и u = 57 кгс/м2. По формуле (2.28) определено, что через T = 25 лет возможно максимальное скопление снеговой нагрузки до 137 кгс/м2 (поэтому г. Омск с 2003 г.

отнесён к III снеговому району), через 50 лет − до 155 кгс/м2, через 100 лет − до 172 кгс/м2 и через 150 лет − до 182 кгс/м2.

86

В среднем в г. Омске за зиму бывает 159 дней со снежным покровом, устойчивое его залегание продолжается обычно в течение 149 дней (106 – 184) [27]. Данные по декадной высоте снежного покрова за 1936 – 1975 гг. приведены в табл. 2.15. Важными характеристиками снеговой нагрузки могут быть продолжительность сильных снегопадов (в г. Омске от 4 до 24 часов) и масса снега, выпадающая при этом (в г. Омске до 40 % расчётной снеговой нагрузки).

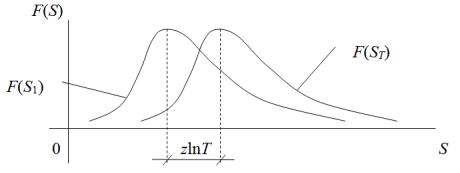
Переход к распределению максимумов за Т лет осуществляется увеличением u на zlnТ в формуле (2.29) и приводит к соответствующему смещению кривой теоретического распределения вдоль оси абсцисс (рис. 2.2).

вующей пониженному её значению, по данным В.Д. Райзера, на уровне значимости 5% не противоречит нормальному закону.

Для вероятностных расчётов и оценки надёжности конструкций, находящихся под действием снеговой нагрузки, точные данные по ко-

торой отсутствуют, можно принять среднегодовую нагрузку S1 равной нормативному значению, регламентированному прежними нор-

мами (см. табл. 2.13, например, для г. Омска S1 = 0,7 кПа). Остальные параметры находятся из совместного решения уравнений (2.27) − (2.30) при расчётных значениях T = 25 лет и ST = S25.

87

Пример 2.2. Получить приближённую оценку стандартного отклонения sS ежегодных максимумов снеговой нагрузки на поверхности земли для условий г. Омска.

Среднее значение ежегодных максимумов составляет S1 = 0,7 кПа (II район, см. табл. 2.13). Максимальное значение снеговой нагрузки за период Т = 25 лет соответствует расчётному значению и составляет S = SТ = S25 =1,8 кПа

(III район, см. табл. 2.12). Из условия (2.30) получаем z = (SТ − S1)/lnТ = (1,8 –

– 0,7)/ln25 = 0,34 кПа, а из (2.27) sS = s = 1,28255z = 0,44 кПа.

Пример 2.3. Определить вероятность превышения нормативного значе-

ния нагрузки в условиях г. Омска в течение одной зимы при полученных в пр и- мере 2.2 параметрах снеговой нагрузки S1 = 0,7 кПа и sS = 0,44 кПа.

Пример 2.5.СПри полученных в примерах 2.2 и 2.3 параметрах определить расчётное значение снеговой нагрузки с периодом повторяемости Т = 50 лет.

Расчётное значение определяется из формулы (2.28) с учётом замечаний к формуле (2.29): SТ = S50 = 0,5 + 0,34ln50 + [−ln(ln50/49)]0,34 = 3,16 кПа.

88