
1819
.pdfФедеральное агентство по образованию Сибирская государственная автомобильно-дорожная академия (СибАДИ)
Т.А. Мызникова
МОДЕЛИ СОЦИАЛЬНО - ЭКОЛОГО -
ЭКОНОМИЧЕСКИХ СИСТЕМ Учебно - методическое пособие
Омск Издательство СибАДИ
2008
УДК 519.6 ББК 22.181 М91
Рецензенты:
канд. техн. наук, доц. В.Н. Задорожный (ОмГТУ),
канд. физ.-мат. наук В.В. Лизунов (ОНОК)
Работа одобрена редакционно-издательским советом академии в качестве учебно - методического пособия для специальностей 080801, 090105.
Мызникова Т.А.
М91 Модели социально - эколого - экономических систем: Учебно - методическое пособие. – Омск: Изд-во СибАДИ, 2008 – 62 с.
ISBN 978-5-93204-421-6
Учебно-методическое пособие содержит сведения по теоретическим основам прогнозирования социально - экологоэкономических систем на основе моделей с обыкновенными дифференциальными уравнениями, включая использование метода качественного исследования систем обыкновенных дифференциальных уравнений. Рассматриваются вопросы использования метода биологической аналогии для исследования социальных и экономических процессов.
Пособие содержит набор тестов для самопроверки студентов.
Разработано для студентов специальностей 080801, 090105 в рамках курсов «Основы прогнозирования», «Математические основы прогнозирования», но может использоваться и студентами других специальностей для самостоятельного изучения этой дисциплины.
Ил 44. Библиогр.: 6 назв.
ISBN 978-5-93204-421-6 |
© Т.А. Мызникова, 2008 |
2
ВВЕДЕНИЕ
Одним из современных методов исследования социально - эколого - экономических процессов является математическое моделирование этих процессов на основе обыкновенных дифференциальных уравнений (ОДУ). В настоящее время существует достаточно большое количество хорошо изученных динамических моделей различных экологических процессов. С другой стороны, развитие вычислительной техники предоставляет дополнительные возможности по исследованию систем ОДУ на основе проведения вычислительных экспериментов.
Но по аналогии можно исследовать и динамические социальноэкономические процессы. Успехи применения метода математического моделирования в естествознании стимулировали разработку нелинейных моделей динамических социально-экономических процессов. Рассмотрение метода экологической (биологической) аналогии является актуальным в настоящее время, кроме того, рассматриваемые модели представляют интерес сами по себе. В пособии рассмотрены простейшие динамические социально-экономические модели, позволяющие сделать оценки среднегодовых темпов роста при ограниченной информации, рассмотреть процессы неравномерного развития в экономике, а также моделировать ситуацию конкуренции на рынке между предприятиями и т.п. Анализ этих моделей полезен с практической точки зрения, так как он служит основой сложных прогнозных моделей различных социально-экономических процессов.
Большая часть пособия посвящена моделям классической экологии, как наиболее изученным моделям.
Повышенный интерес к экологической тематике, быстрое развитие вычислительной техники позволяют надеяться на возможность машинной имитации сложных экологических связей и взаимодействий. Для этого прежде всего требуется наличие моделей динамики различных популяций.
3
1. МОДЕЛИ ДИНАМИКИ ПОПУЛЯЦИЙ
Увеличение масштабов воздействия человека на природную среду привело к необходимости разработки специальных программ охраны окружающей среды и рационального использования природных ресурсов, таких как повышение продуктивности сельскохозяйственных посевов и естественных угодий, выбор наилучшего режима вылова рыб или отстрела животных, борьба с эпидемиями, вредителями лесного и сельского хозяйства, хищниками, паразитами и т. п.
Основная цель, стоящая перед экологами, – оптимизация стратегии управления состоянием окружающей среды. Важнейшей частью основной проблемы является задача такого регулирования численности популяций, при котором сохраняется и преумножается продуктивность полезных видов и сводится к минимуму уровень численности вредителей. Вопросы, возникающие при решении этой задачи, имеют много общего независимо от конкретного вида биологических популяций. Для всех популяций характерны такие процессы, как рождение и гибель особей, их расселение, хищничество, конкуренция, паразитизм, распространение заболеваний, изменения, связанные с воздействием на животных и растения, климатических условий среды обитания.
В классической экологии рассматриваются взаимодействия нескольких типов:
взаимодействие организма и окружающей среды;
взаимодействие особей внутри популяции;
взаимодействие между особями разных видов, т.е. между популяциями.
При построении модели классической экологии используется опыт
математического моделирования механических и физических систем, но при этом учитываются следующие специфические особенности биологических систем:
сложность (биологического) внутреннего строения каждой
особи;
зависимость условий жизнедеятельности организмов от многих факторов внешней среды;
незамкнутость экологических систем;
большой диапазон внешних характеристик, при которых сохраняется жизнеспособность систем.
Моделирование любой экосистемы включает два этапа:
1)процесс конструирования моделей, основанный на использовании как общих теоретических представлений об изучаемом объекте, так и конкретных экспериментальных данных;
4

2) математическое исследование уже построенных моделей и интерпретация полученных результатов.
Детерминированный подход к изучению динамики экосистем связывается с применением дифференциальных уравнений или уравнений в конечных разностях.
1.1. Модель роста численности популяции
Одной из простейших моделей классической экологии является модель роста численности популяции при избытке пищи и отсутствии других ограничивающих факторов, описываемая дифференциальным уравнением экспоненциального роста.
Рождаемость характеризует частоту появления новых особей в популяции. Различают рождаемость абсолютную и удельную. Абсолютная рождаемость – число особей, появившихся в популяции за единицу времени. Удельная рождаемость выражается в числе особей на особь в единицу времени. Например, для популяции человека как показатель удельной рождаемости обычно используют число детей, родившихся в год на
1000 человек. Смертность (абсолютная и удельная) характеризует ско-
рость убывания численности популяции, вследствие гибели особей от хищников, болезней, старости и т.д.
Используя такие параметры модели изменения численности популяции, Томас Мальтус (1766–1834) сформулировал экспоненциальную модель. В книге «О росте народонаселения» Мальтус опубликовал в 1798 г. результаты своих исследований, основанных на данных о росте населения в американских колониях. Введем обозначения:
N(t) – численность популяции в момент времени t;
dN – скорость роста численности популяции; dt
A– число особей в популяции, рождающихся в единицу времени;
B– число особей в популяции, умирающих в единицу времени.
Тогда скорость роста численности популяции будет равна: dN A B, dt
где A a N (a – коэффициент естественной рождаемости) и B b N (b – коэффициент естественной смертности), и a, b – положительные константы. Учитывая это, запишем скорость роста численности популяции как
dN N (a b). Если разницу между естественной рождаемостью и естест- dt
венной смертностью обозначить за r, т.е. r a b, то выражение примет следующий вид:
5
dN |
r N . |
(1.1) |
|
||
dt |
|
|
Данное уравнение и есть модель Мальтуса, где r – коэффициент прироста численности популяции, или мальтузианский коэффициент.
Для исследования данной модели необходимо решить приведенное дифференциальное уравнение.
|
|
Произведем разделение |
переменных: |
|
dN |
|
r dt. Проинтегрируем: |
||||||
|
|
|
|||||||||||
|
dN |
|
|
|
|
|
N |
|
|
|
|
||
|
r dt = > ln N r t c. |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
N |
и N N0 => lnN0 |
r t0 c . Выразим константу: с lnN0 |
|
|
|
|||||||
|
|
При t t0 |
r t0 |
||||||||||
и подставим: |
lnN r t lnN0 r t0 . |
|
|
|
|
|
|
|
|
|
|||
|
|
Проведя |
следующие преобразования: |
ln |
N |
r (t t0 ) => |
r(t t0 ) |
|
N |
, |
|||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
N0 |
|
|
N0 |
|||
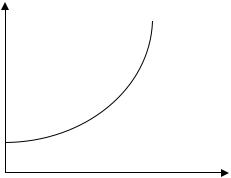
получим решение дифференциального уравнения (1.1) N(t) N0 |
r(t t0 ) . |
|
|
|
|||||||||
1.1. |
Графическое представление найденного решения приведено на рис. |
||||||||||||
|
|
В литературе приводится много |
|||||||||||
|
N |
|
|||||||||||
|
|
|
|
примеров быстрого роста численности |
|||||||||
|
|
|
N (t) |
популяций (простейшие и т.д.). На ко- |
|||||||||
|
|
|
|
ротких промежутках времени эта мо- |
|||||||||
|
|
|
|
дель хорошо описывает динамику этих |
|||||||||
популяций.
N0
t
t0
Рис.1.1. График изменения численности популяции
1.2. Модель внутривидовой конкуренции
Уравнение в модели Мальтуса фактически описывает максимальную биологическую продуктивность вида и справедливо лишь для коротких промежутков времени, когда ограниченность среды обитания еще не препятствует росту. В реальных условиях ни одна популяция не может полностью реализовать свой биологический потенциал. Численность ее всегда ограничивается внешней средой. Уравнение Мальтуса следует изменить так, чтобы учесть внутривидовую конкуренцию, которая возникает из-за ограниченности ресурсов.
6
Следует отметить, что конкуренцию можно определить, как использование некоторого ресурса (пищи, воды, пространства) каким-либо организмом, которое тем самым уменьшает доступность этого ресурса для других организмов. Внутривидовой конкуренцией называется взаимодействие между конкурирующими организмами, если они принадлежат к одному виду. Если они относятся к разным видам, то – межвидовой конкуренцией.
К факторам, ограничивающим численность популяции, относятся недостаток ресурсов питания, освещения, пространства, а также продукты жизнедеятельности популяции.
В результате вместо экспоненциальной зависимости возникает логи-
стическая.
Если в модели Мальтуса dN r N dt
коэффициент b записать как b m N ,
где m – коэффициент естественной смертности,– коэффициент зависимости смертности от численности популяции, то получим
dN N (a m N). dt
|
|
|
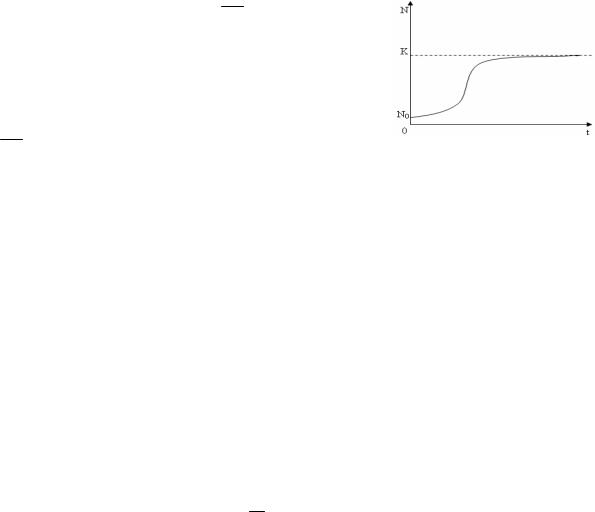
Рис. 1.2. Логистический |
|
|
|
вид зависимости |
После преобразования выражение примет вид |
|
||
|
dN |
(r N) N . |
(1.2) |
|
|
||
|
dt |
|
|
Данное уравнение описывает модель внутривидовой конкуренции.
Выражение в скобках – это удельная скорость роста популяции. Причем чем больше численность популяции N(t), тем меньше скорость роста. Математическое описание внутривидовой конкуренции впервые предложено
в 1838 г. Ферхюльстом. |
|
|
|
|
|
вынести за скобки r, то |
||||||||
|
dN |
Если |
в |
правой части |
уравнения |
|||||||||
|
N r(1 |
|
N) , и обозначить |
|
|
за |
1 |
, |
тогда уравнение можно перепи- |
|||||
|
dt |
dN |
r |
|
K N |
|
|
r |
K |
|
||||
сать так: |
r N( |
) . |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
dt |
|
K |
|
|
|
|
|
|
|||
При малых N значением N можно пренебречь и тогда рост числен-
K
ности идет по экспоненциальному закону, при возрастании N и неизменном К рост численности будет замедляться, и при N, близком к величине K, рост остановится. Величину K называют емкостью среды. Она отражает возможности среды обитания предоставить популяции нужные для ее роста ресурсы.
7
Для исследования модели необходимо решить данное уравнение. В качестве начальных условий взято, что при t t0 N(t0)=N0. Проинтегриро-
вав, получим N(t) |
|
K N0 |
|
. |
|
|
|
||
|
N0 (K N0 ) exp( r (t t0 )) |
|||
N |
|
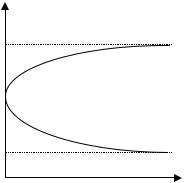
На рис. 1.3 представлен вид зави- |
||
K1 |
|
симости N(t) для разных соотношений |
||
|
начальной численности популяции и |
|||
|
|
|
||
|
K1>N0 |
|
емкости среды. Логистическая кривая |
|
N |
|
дает хорошее совпадение с экспери- |
||
|
K2<N0 |
|
ментальными данными, что говорит об |
|
|
|
адекватности модели. |
||
K2 |
|
|
|
|
t0 |
t |
|
|
|
Рис.1.3. Изменение численности популяции при различных начальных значениях
Условия применимости дифференциальных уравнений (модель Мальтуса и модель Ферхюльста) для описания роста популяций могут быть сформулированы следующим образом:
1)в моделях не учитываются индивидуальные различия особей одного вида. Популяция представляется состоящей из одинаковых особей со средними характеристиками рождаемости и смертности неизменными во времени. Пространственное распределение особей считается однородным;
2)размножение и смертность популяций считаются происходящими непрерывно без временных сдвигов между поколениями. Это справедливо для роста бактерий, дрожжей, микроводорослей и других организмов, не обладающих возрастной структурой;
3)достаточно высокая численность популяции, т.е. если число особей мало, усредненные характеристики вводить нельзя. Необходимо учитывать дискретность популяции, т.е. использовать вероятностный подход.
1.3.Модель «сбор урожая»
Рассмотрим модель популяции, численность которой зависит не только от внутривидовой борьбы, но и от отлова. В качестве такой популяции можно рассмотреть «стада промысловых рыб». Интенсивность отлова обозначим Q, т.е. Q – это число особей, вылавливаемых в единицу времени, причем Q>0. В этом случае уравнение получается из модели Ферхюльста (1.2) и принимает следующий вид:
dy/dt y(a by) Q, |
(1.3) |
8
где a – мальтузианский коэффициент;
b – коэффициент внутривидовой конкуренции.
Требуется определить, при каком максимальном значении квоты отлова Q популяция не исчезнет.
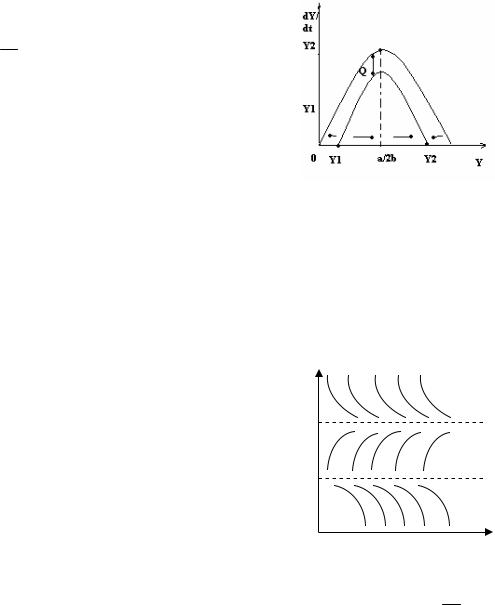
Для решения этой задачи заметим, что на плоскости YOY’ (рис. 1.4) уравнение (1.3) задает параболу, ветви которой направлены вниз.
Стационарное решение не зависит
от времени dy 0, поэтому ay by2 Q 0, dt
D a2 4Qb и значит |
a2 |
Q . |
|
4b |
|||
|
|
|
|
|
|
|
|
Рис. 1.4. Зависимость скорости |
|||
|
|
|
|
|
|
роста популяции от ее числен- |
|||
|
|
|
|
|
|
ности при 0 Q |
a2 |
|
|
|
|
|
|
|
|
4b |
|||
|
|
|
|
|
|
|
|||
При этом в случае Q |
a2 |
|
квадратный трехчлен by2 ay Q имеет два |
||||||
4b |
|||||||||
|
|
|
|
|
|
|
|||
положительных корня: |
y1 и y2 . Это значит, |
что дифференциальное урав- |
|||||||
нение (1.3) имеет два стационарных решения y y1 и y y2 (рис.1.5). |
|||||||||
Поскольку правая часть уравнения (1.3) |
Y |
||||||||
отрицательна при y y1 |
и y y2 |
и |
|||||||
|
|
|
|||||||
положительна при y y y |
2 |
, то решения |
y2 |
||||||
1 |
|
|
|
|
|
|
|
||
уравнения (1.3) при y y1 и y y2 |
|
|
|
||||||
монотонно убывают, а при y1 y y2 – |
y1 |
||||||||
монотонно возрастают. |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
Из этого следует, что любое случайное |
|
|
|
||||||
отклонение от стационарного решения |
|
|
t |
||||||
y y2 гасится. |
|
|
|
|
|
Рис. 1.5. Динамика численности |
|||
|
|
|
|
|
|
||||
популяции при 0 Q a2
4b
Если происходит по какой-либо причине случайное отклонение от стационарного решения y y1 вверх, то это приводит к дальнейшему росту численности популяции до величины y y2 . В случае же отклонения от решения y y1 вниз численность решения популяции сокращается до нуля, что соответствует катастрофической ситуации. Таким образом,
9
стационарное решение уравнения (1.3) является неустойчивым, а решение y y2 – устойчивым .
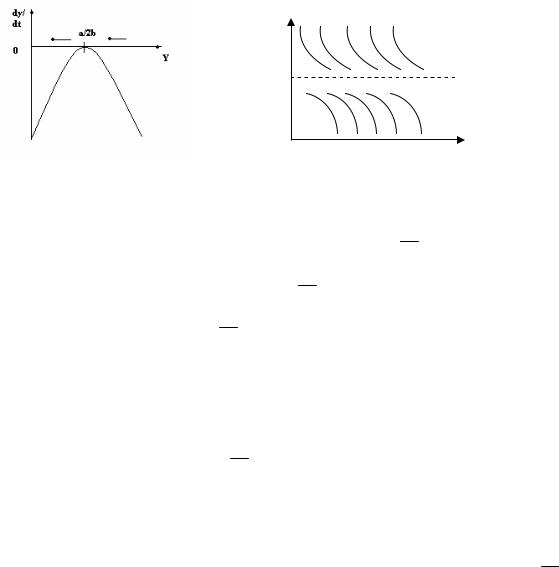
Что произойдет при увеличении квоты отлова Q? По мере увеличения параметра Q эта парабола будет смещаться вниз (рис. 1.6), вследствие чего значения y1 и y2 будут сближаться.
Y |
б) |
a/2b |
|
|
t |
а) |
б) |
Рис. 1.6. Зависимость скорости роста популяции от ее численности (а)
и динамика численности (б) при Q a2
4b
Как видно из рис. 1.6,a, при Q a2 правая часть уравнения (1.3) отри-
4b
цательна всюду, кроме y a , где она обращается в нуль. Это значит, что
|
|
2b |
||
при Q |
a2 |
стационарное решение y |
a |
дифференциального уравнения |
|
4b |
|
2b |
|
(1.3) является неустойчивым: любое случайное отклонение вниз от этого решения приводит к падению численности популяции до нуля (см. рис.
1.6,б). Понятно, что при Q a2 популяция также гибнет, поскольку в этом
4b
случае производная y' всегда отрицательна.
Итак, стремление максимизировать квоту отлова приводит к потере устойчивости решения, следствием чего является катастрофа: популяция
погибает. Как следует изменить стратегию, чтобы при отлове Q a2 чис-
4b
ленность популяции не падала бы до нуля при малых случайных отклонениях от стационарного решения?
Оказывается, что устойчивость не теряется в случае введения обратной связи, которая в данном случае означает замену жесткого плана Q const гибким, когда, например, квота отлова Q пропорциональна численности популяции: Q c y.
Модель и в этом случае удобно исследовать на устойчивость, используя плоскость YOY '. На рис. 1.7a хорошо видно, что правая часть уравне-
10
