
1819
.pdf
2.1.2. Устойчивость линейных систем 2-го порядка
Пусть в системе дифференциальных уравнений (ДУ) (2.1) функции F(N1, N2) и G(N1, N2) – линейные функции относительно N1 и N2, т.е.
|
F(N1 ,N2 |
)=a11N1 +a12N2 ; |
|||||||||
|
|||||||||||
|
|
,N |
|
)=a |
|
N |
|
+a |
|
N |
|
G(N |
2 |
21 |
1 |
22 |
2 . |
||||||
|
1 |
|
|
|
|
|
|||||
Тогда в векторной форме система (1.1) запишется следующим обра-
зом:
_
N |
1 |
AN , где |
_ |
N |
1 |
|
, |
|
N |
|
|||||
dt |
|
|
|||||
|
|
|
N2 |
|
|||
N1 |
|
|
|
||
_ |
|
|
|
|
|
dt |
(2.2) |
||||
N |
|
. |
|||
N2 |
|
|
|
||
|
dt |
|
|
|
|
|
|
|
|
||
Собственными числами матрицы А называются корни характеристического многочлена det(А- I)=0, где det(А- I) – определитель матрицы
a11 |
a12 |
|
|
a22 |
. |
a21 |
|
Характеристический многочлен для системы 2-го порядка имеет тоже второй порядок:
det A I 2 p q 0. |
(2.3) |
По теореме Виета
1 2 , |
1 2 q. |
Отсюда следует, что для следа матрицы А (след Tr А – сумма диагональных элементов матрицы А) и определителя det A имеем равенства
Tr A 1 2 - p , |
det A 1 2 q . |
Тогда уравнение (2.3) перепишется в виде
2 |
Tr A det A 0, |
(2.4) |
|||||||
|
|
1 |
Tr A |
1 |
|
|
|
(2.5) |
|
|
D , |
||||||||
|
|
||||||||
1,2 |
2 |
2 |
|
|
|
|
|||
где D – дискриминант уравнения (2.4).
D Tr A 2 4det A .
21
ТЕОРЕМА (критерий устойчивости линейной системы)
Если собственные числа матрицы А линейной системы (2.2) принадлежат левой полуплоскости, то положение равновесия (0,0) асимптотически устойчиво.
Если хотя бы одно собственное число принадлежат правой полуплоскости, то система неустойчива.
Из (2.5) следует, что для систем 2-го порядка условие асимптотической устойчивости выполняется тогда и только тогда, когда Tr A < 0 и det А > 0. При нарушении хотя бы одного из этих условий положение равновесия неустойчиво. У линейных систем точка (0,0) является положением равновесия. Если det A 0, то других положений равновесия нет. От знака дискриминанта D зависит вид собственных значений матрицы А.
1. Если D > 0, то оба собственных числа действительны. В этом случае возможны следующие ситуации:
a) 1 2, 1 > 0, 2 > 0.
Положение равновесия неустойчиво.
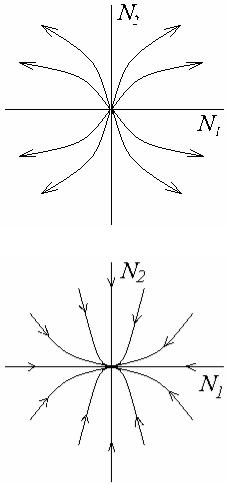
Фазовый портрет в окрестности (N1, N2) для случая a) представлен на рис. 2.1.
Такое положение равновесия называется
неустойчивым узлом.
б) 1 , 2 < 0, 1 2 .
Рис. 2.1.Неустойчивый узел
В этом случае положение равновесия устойчиво, так как оба собственных числа лежат в левой полуплоскости.
Фазовый портрет в окрестности неподвижной точки для случая б) показан на рис. 2.2.
Такое положение равновесия называ-
ется устойчивым узлом.
Рис. 2.2.Устойчивый узел
22
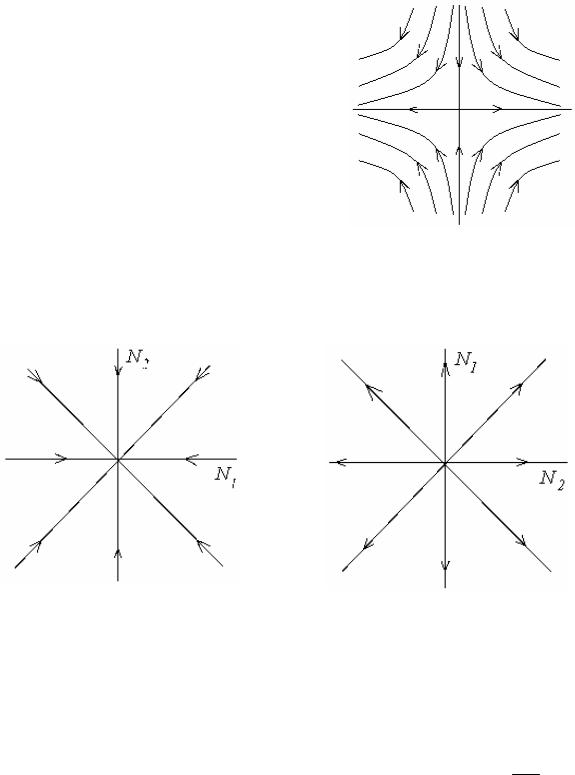
в) 1 > 0, 2 < 0.
Действительные собственные числа противоположных знаков порождают неустойчивое положение равновесия, называемое седлом (рис. 2.3).
В этом случае det А < 0.
2. D = 0. Равные собственные числа. а) 1 = 2 = 0 0 и матрица
А – скалярная (А= I).
Рис. 2.3. Седло |
|
В этом случае положение равновесия называется звездным |
узлом, |
оно устойчиво в случае 0 < 0 (рис. 2.4) и неустойчиво для |
0 > 0 |
(рис.2.5). |
|
Рис. 2.4.Устойчивый звёздный узел Рис. 2.5. Неустойчивый звёздный узел
б) 1 = 2 = 0 0 и матрица А не диагональна. Положение равновесия называется вырожденным узлом . Оно устойчиво , если 0 < 0 (рис.2.6), и неустойчиво при 0>0 (рис. 2.7).
Прямая, на которой траектории меняют свои направления, – геомет-
рическое место точек экстремума для N1 . Оно задается уравнением dN1 =0. dt
23
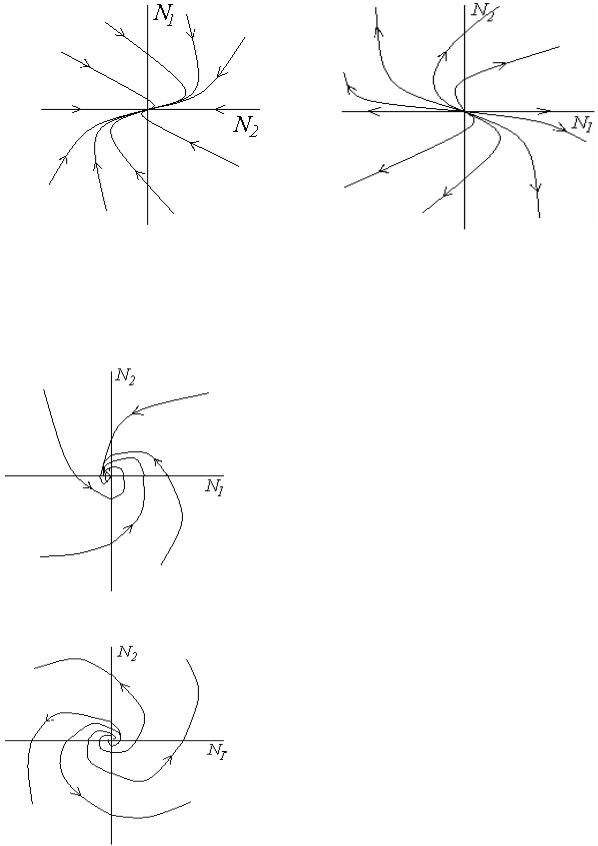
Рис. 2.6. Устойчивый вырожденный узел |
Рис.2.7.Неустойчивый вырожденный |
||
|
|
узел |
|
3. |
D < 0. В этом случае собственные числа комплексны: 1, 2 = |
i . |
|
Возможны следующие ситуации: |
|
|
|
а) < 0. Оба собственных числа лежат в левой полуплоскости, положение равновесия асимптотически устойчиво.
Фазовый портрет имеет вид спирали, накручивающейся на положение равновесия
(рис. 2.8).
Неподвижная точка называется устойчивым фокусом. В системе происходят затухающие колебания.
Рис. 2.8. Устойчивый фокус
б) > 0.
Вэтом случае имеем дело с неустойчивым фокусом.
Всистеме происходят расходящиеся колебания. Фазовый портрет системы представлен на рис.2.9.
Рис. 2.9. Неустойчивый фокус
24
в) = 0.
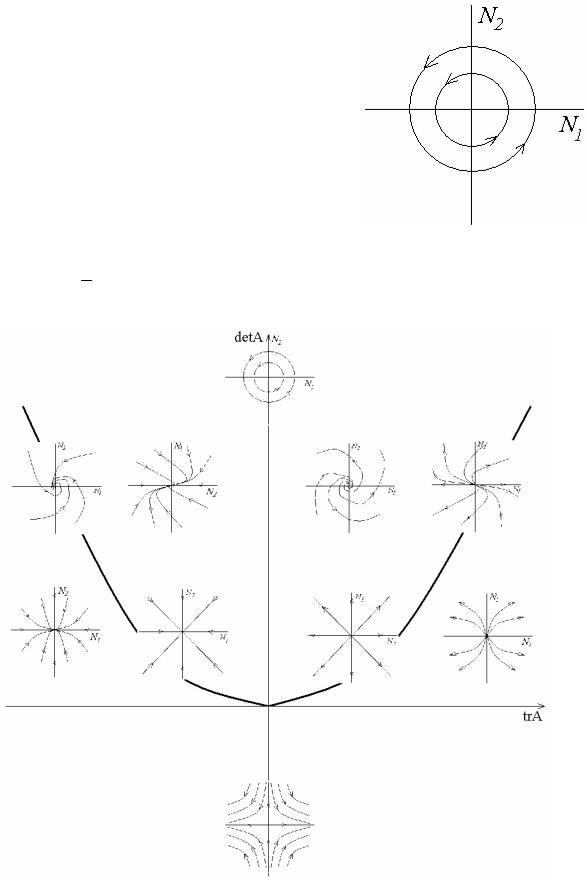
Собственные числа лежат на мнимой оси. Положение равновесия – центр. Фазовый портрет состоит из замкнутых окружностей.
Это единственный случай, когда в системе возникают периодические колебания. Амплитуда колебаний зависит от начальной точки движения системы.
Фазовый портрет изображен на рис. 2.10.
Рис. 2.10. Центр
На рис. 2.11 показан характер зависимости фазовых портретов системы N = A N от следа и определителя матрицы А.
Рис. 2.11 Фазовые портреты исследуемой системы
25
2.1.3. Устойчивость в случае нелинейных систем
Пусть теперь функции F(N1, N2) и G(N1, N2) в системе (2.1) нелинейные. Исследование на устойчивость положения равновесия нелинейных систем на практике сводится к исследованию на устойчивость линейной системы, являющейся линеаризацией (системой первого приближения) для (2.1). Пусть (N10, N20) – неподвижная точка системы (2.1). Линеаризованная в окрестности (N10, N20) система для (2.1) имеет вид
|
|
|
|
N |
= W |
|
, |
|
||||||
|
|
|
|
N |
|
|||||||||
где N |
= N1 |
, а W – матрица Якоби в точке (N10, N20) для системы (2.1): |
||||||||||||
|
N2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
, |
|
|
F |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
N2 |
|
|||||||
|
|
W |
N1 |
|
|
|
|
|
||||||
|
|
|
G |
, |
|
G |
|
|
||||||
|
|
|
|
|
|
|
||||||||
|
|
|
N |
|
N |
|
|
|
||||||
|
|
|
|
|
|
2 |
|
N1 N10 |
||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
N N0 |
||
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
||
ТЕОРЕМА. Если линеаризация асимптотически устойчива, то (N1, N2)
– асимптотически устойчивое положение равновесия для исходной нелинейной системы (2.1). Если у матрицы W есть хотя бы одно собственное число в правой полуплоскости, то положение равновесия (N1, N2) неустойчиво.
2.2.Экологические модели
Вэтом параграфе исследуются некоторые нелинейные модели динамики популяций методом качественного исследования систем обыкновенных дифференциальных уравнений. В п. 2.2.1 рассмотрено исследование модели о двух конкурирующих видах, в п. 2.2.2 – различные модификации модели «хищник – жертва», а в п. 2.2.3 изучаются две модели распространения эпидемии.
2.2.1. Модель конкуренции двух видов (модель 1)
Пусть два вида животных конкурируют друг с другом на некоторой территории с ограниченными запасами пищи. Возможны различные исходы их конкурентной борьбы:
а) вид 1 выживает, а вид 2 умирает; б) вид 2 выживает, а вид 1 умирает; в) оба вида сосуществуют; г) оба вида вымирают.
26
Каждый из этих исходов соответствует некоторому положению равновесия для популяции N1 и N2 двух рассматриваемых видов. Поэтому дифференциальные уравнения, моделирующие динамику популяций N1 и N2 , должны иметь 4 положения равновесия.
Рассмотрим следующие нелинейные динамические уравнения:
dN |
1 |
|
a b N1 |
s N2 N1 ; |
|
|
|
|
|||
|
|
||||
dt |
|
|
|
(2.6) |
|
|
|
|
|
|
|
dN2 |
|
c g N1 |
d N2 N2 , |
||
|
dt |
|
|
||
|
|
|
|
|
|
где a, b, c, d, s, g > 0.
Здесь a и c – интенсивности роста для видов 1 и 2 соответственно (скорости размножения изолированных популяций N1 и N2 ); члены –b N1 и –d N2 соответствуют внутривидовой конкуренции, а члены –s N2 и
–g N1 соответствуют межвидовой конкуренции. Необходимое условие для возможности выживания обоих видов состоит в том, что должна существовать неподвижная точка системы (2.1), обе координаты которой положительны. Т.к. смысл N1 и N2 – численность популяций, нас интересуют только неподвижные точки, лежащие в первом квадранте плоскости N1, N2 . Найдем неподвижные точки системы (2.6):
a b N |
|
|
s N |
|
N |
|
|
0; |
|
|
1 |
|
2 |
|
|
1 |
|
(2.7) |
|
c g N |
2 |
d N |
2 |
N |
2 |
0. |
|||
|
|
|
|
|
|
|
|||
Неподвижные точки системы (2.6) – это решения системы (2.7).
1.Очевидно, точка (0,0) есть неподвижная точка системы (2.6). Этой точке соответствует случай вымирания обоих видов животных.
2.Вторую неподвижную точку найдем из условий
N1= 0, c – g ·N1 – d·N2 = 0.
Искомая точка лежит на пересечении оси координат 0N2 и прямой N2 = c/d – g/d·N1. Координаты точки равны (0, c/d), ей соответствует случай вымирания первого вида.
3.Аналогично находится третья неподвижная точка системы с координатами (a/b, 0), что соответствует вымиранию второго вида.
4.Для нахождения четвертой неподвижной точки нужно решить систему уравнений:
a bN1 sN2 0;
с gN1 dN2 0,
27

N1 a/b s/b N2 ,
c g a/b s/b N2 dN2 0,
N2 cb ag .
Итак, искомая точка лежит на пересечении двух прямых а – bN1 - sN2 = 0 и c – gN1 – dN2 = 0 и имеет координаты
ad sc cb ag . bd gs bd gs
Так как нас интересуют в этом случае только положительные координаты, то должны выполняться следующие условия:
а) bd – gs > О , ad – sc > 0 , cb – ag > 0 либо б) bd – gs < О , ad – sc < 0 , cb – ag < 0.
Вероятность какого-либо исхода конкурентной борьбы зависит от устойчивости соответствующего положения равновесия.
Рассмотрим случай выполнения условий б). ( Исследование в случае а) предлагается проделать самостоятельно.) После нахождения неподвижных точек системы (2.6) для исследования поведения решения произведем линеаризацию этой системы в окрестностях точек покоя. Каждую из линеаризованных систем запишем в виде
N = W N ,
где W – матрица Якоби.
1. Матрица Якоби для точки (0,0):
F |
|
F |
|
|
|
|
|
||
|
|
|
|
|
a 2bN |
|
sN |
|
|
|
|
|
|
||||||
W N1 |
|
N2 |
|
|
1 |
|
2 |
||
G |
|
G |
|
gN2 |
|
||||
|
|
|
|||||||
|
|
|
|
|
|
||||
N1 |
|
N2 |
|
|
|
|
|
||
sN |
1 |
|
|
a |
0 |
||
|
|
|
|
|
|
|
|
c gN1 2dN |
|
|
|
0 |
c |
|
|
2 N |
0 |
|
|
||||
|
|
1,2 |
|
|
|
|
|
detW = ac > о , TrW = a + c > 0 , следовательно , положение равновесия неустойчиво (рис. 2.11). Составим характеристическое уравнение
a |
0 |
|
2 |
|
|
|
|
|
(a )(c ) |
|
(a c) ac 0. |
det(W I) det |
0 |
|
|
||
|
c |
|
|
|
|
28

Это уравнение можно было составить, используя (2.4).
|
|
1 |
|
1 |
|
|
|
1 |
|
1 |
|
|
|
|
1 |
(a c) |
1 |
|
|
|
|
TrW |
|
|
|
(a c) |
|
(a c)2 |
4ac |
(a c). |
|||||||||
|
D |
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||
1,2 |
2 |
2 |
2 |
2 |
|
|
2 |
2 |
|
||||||||||
1 = a > 0 , 2 = c > 0 .
Так как оба собственных числа положительны, то, согласно п. 2.1.1, положение равновесия (0,0) есть неустойчивый узел. Все траектории сис-
|
|
sc |
|
|
||
a |
|
|
|
0 |
|
|
|
d |
|||||
W |
|
|
|
|
||
|
|
|
c |
|
|
|
|
g |
|
|
|
c |
|
|
d |
|||||
|
|
|
|
|
||
темы удаляются от точки (0,0), отсюда следует, что вымирание видов при наличии достаточного ресурса пищи и в предложении, что нет других воздействий внешней среды, влияющих на численность популяций, кроме учитываемых нами случаев межвидовой и внутривидовой конкуренции, невозможно.
detW c(a sc) c(sc a),
|
d |
|
d |
||
TrW a c |
sc |
|
|
ad cd sc |
0. |
|
|
||||
dd
2.Для точки (0, c/d) матрица Якоби имеет вид:
|
|
sc |
|
|
|
|
|
|
sc |
|
sc |
|
||||||
a |
|
|
|
0 |
|
detW c(a |
|
|
|
|
) |
c( |
|
a), |
|
|||
|
|
|
|
d |
|
|
|
|||||||||||
|
d |
|
|
|||||||||||||||
W |
|
|
|
|
|
|
|
|
|
|
|
d |
|
|||||
|
|
|
c |
|
. |
|
|
sc |
|
|
ad cd sc |
|
||||||
|
g |
|
|
c |
TrW |
a c |
|
|
|
|
|
|
|
|
0, |
|||
d |
|
|
|
|
|
|
|
|||||||||||
|
d |
|
d |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
так как рассматривается случай б), когда выполняются условия ad – sc < 0,
то |
detW c |
sc ad |
0 |
. При этом выполнение условий Tr W < 0 и |
|
||||
|
|
d |
|
|
det W > 0 означает для систем 2-го порядка асимптотическую устойчивость положения равновесия. Таким образом, вымирание первого вида вполне возможно.
УПРАЖНЕНИЕ 1. Доказать, что при выполнении условий б) вполне возможно вымирание 2-го вида. (Примечание. Какой из видов будет вымирать, первый или второй, зависит от начальных условий.)
Рассмотрим теперь неподвижную точку
|
|
cb ag |
|
|
|
ad sc |
|
|
|
|
|
|
||
|
|
|
. |
|
bd gs |
|
bd gs |
||
29
Матрица Якоби:
|
|
|
ad sc |
bc ag |
|
|
|
ad sc |
|
|
|
|
|
|||||||
|
a 2b |
|
|
s |
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
W |
|
bd sg |
bd sg |
|
|
|
bd sg |
|
|
|
|
|
||||||||
|
|
|
|
bc ag |
|
|
ad sc |
bc ag |
|
|
|
|||||||||
|
|
|
g |
|
|
|
c |
g |
|
|
|
2d |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
bd sg |
|
|
bd sg |
bd sg |
|
|
|
|||||||||
|
1 |
a(bd sg) 2b(ad sc) s(bc ag) |
|
|
s(cs ad) |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
g(ag bc) |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
bd sg |
|
|
|
|
|
|
|
|
c(bd sg) g(ad sc) 2d(bc ag) |
|
|||||||||
|
1 |
bcs adb |
s(sc ad) |
|
|
1 |
|
b(cs ad) |
s(sc ad) |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bc) |
d |
|
|
|
||
|
bd sg g(ag bc) |
adg bcd |
|
bd gs g(ag |
(ag bc) |
|
|
|||||||||||||
detW |
bd(cs ad)(ag bc) gs(sc ad)(ag bc) |
|
(cs ad)(ag bc)(bd gs) |
|
|
(bd sg)2 |
(bd sg)2 |
||||
|
|
|
(cs ad)(ag bc) 0, bd sg
так как выполнены условия б).
Итак, в предположении, что выполняется условие б), det W < 0, откуда
|
|
|
cb ag |
|
|
|
следует, что положение равновесия |
|
ad sc |
|
|
является седлом. |
|
|
|
|
||||
|
|
|
|
|||
|
bd gs |
|
bd gs |
|
||
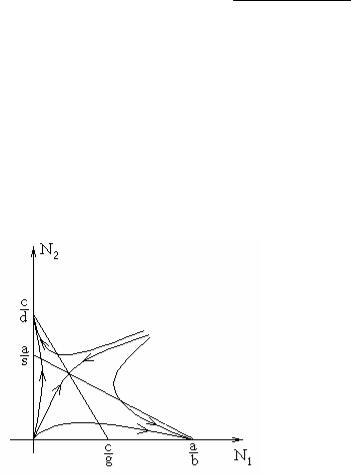
Заметим, что в случае выполнения условий а) det W > 0 . Фазовый портрет системы (2.6) для случая выполнения условий bd – gs < 0 , ad – sc < 0 , cb – ag < 0 (т.е. условий б) ) изображен на рис. 2.12 .
Видим, что сосуществование для двух конкурирующих видов является чрезвычайно маловероятным, так как при t в эту точку входят только две траектории, а все остальные удаляются от нее.
Предполагая, что начальные положения (начальные численности исследуемых популяций) равновероятны, видим, что наиболее вероятным исходом является вымирание одного из видов. Полученный результат находится в соответствии с "принципом конкурентного исключения" Гаузе, согласно которому в таких ситуациях конкурентной борьбы один из видов вымирает.
Рис.2.12. Фазовый портрет системы для условия б)
УПРАЖНЕНИЕ 2. Доказать, что при выполнении неравенств а) получаем противоположный экологический вывод:
30
