1819

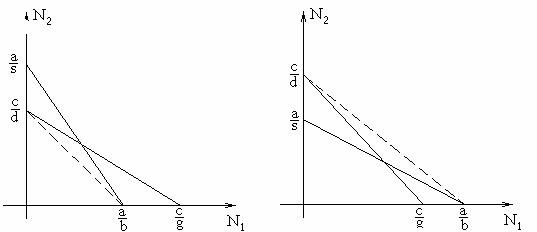
невозможно вымирание одного из видов, оба вида животных сосуществуют вместе.

Таким образом, выполнение условий а) влечет устойчивость нетривиальной неподвижной точки. На рис. 2.13 и 2.14 соответственно показан геометрический смысл условий а) и б).

Для устойчивости (т.е. для сосуществования) точка равновесия должна лежать над прямой, соединяющей (a/b, 0) и (0, c/d).

Биологическая интерпретация условий а), обеспечивающих устойчивость положения равновесия, заключается в следующем: если истинные скорости роста а и с в задаче (2.6) одинаковы, то b>g и d>s , т.е. увеличение численности одного из конкурентов сильнее подавляет его собственный рост, чем рост другого конкурента.

2.2.2.Модели “хищник-жертва" (модели 2а, 2б, 2в, 2г)

Рассмотрим модель, содержащую два вида, один вид – хищник, а другой – их добыча. Пусть N1 и N2 – популяции жертв и хищников соответственно. Сделаем следующие предположения:

а) между особями одного вида нет соперничества; б) любая жертва может найти достаточно пищи для пропитания;

в) при любой встрече хищника и жертвы хищник убивает жертву (т.е. гибель жертвы пропорциональна количеству N1 и N2 .

2.2.2.1. Динамика популяций в этих предположениях описывается следующей системой дифференциальных уравнений для модели 2а.

где N1– численность жертв;

N2 – численность хищников;

31

а>0 – скорость размножения (интенсивность роста) при отсутствии хищников;

с>0 – интенсивность вымирания хищников в отсутствии жертв; b>0 – коэффициент потери биомассы жертв хищников;

d>0 – коэффициент увеличения биомассы хищников в случае удачной охоты (чем больше жертв, тем больше биомасса хищников).

Система (2.8) имеет две неподвижные точки: (0,0) и (c/d, a/b). Матрица Якоби для точки (0,0) имеет вид

det W = -ac < 0 , отсюда следует, что начало координат – неустойчивое положение равновесия (седло). Найдем матрицу Якоби для точки покоя (c/d, a/b):

detW = ac > 0 , TrW = 0 .

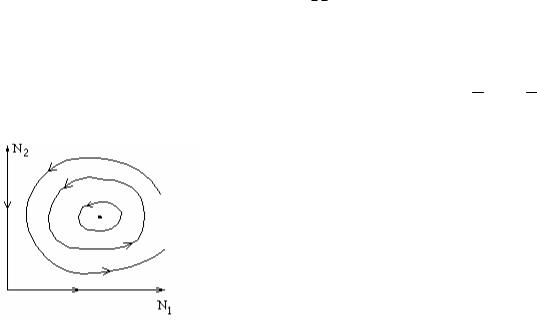
Согласно рис. 2.15 исследуемая точка – центр, траекториями системы будут замкнутые кривые, в которые преобразуются за счет нелинейности системы (2.3) окружности – траектории линейной системы N W N .

Фазовый портрет для модели 2а изображен на рис. 2.15.

Наличие траекторий, имеющих вид замкнутых кривых, означает, что система совершает колебательные движения вокруг неподвижной точки (c/d, a/b). Амплитуда колебательного процесса зависит от того, как близки начальные условия к положению равновесия. Чем ближе к центру расположена начальная точка( N1(t0), N2(t0) ) движения системы, тем меньше будет амплитуда колебаний.

Рис. 2.15. Общий фазовый портрет исследуемой системы

2.2.2.2. Рассмотрим следующую модель "хищник–жертва" Вольтерра (модель 2б). Изменим теперь уравнение для жертвы, введя член, уменьшающий численность популяции за счет внутривидовой конкуренции. Система примет такой вид:

32

где k – коэффициент внутрипопуляционной конкуренции. Введение члена

– kN1 означает, что в отсутствии хищников рост численности жертв будет происходить в соответствии с логистическим уравнением: а/k – емкость среды для жертвы.

Найдем точки покоя для системы (2.9):

(a kN1 bN2 )N1 0;

( c dN1)N2 0.

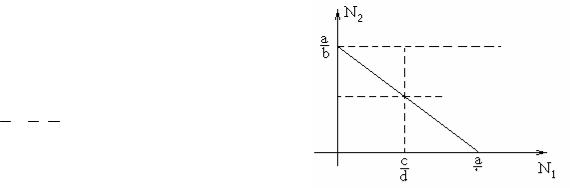
Очевидно, точка (0,0) есть неподвижная точка, вторая неподвижная точка лежит на пересечении двух прямых (рис. 2.16):

В экологических моделях рассматривают только точки (N1, N2), имеющие неотрицательные значения. N2 будет больше 0 тогда и только тогда, когда выполняется

условие a k c . b b d

Рис. 2.16. Положение второй неподвижной точки

Это условие при положительных a, b, c, d и k – равносильно неравен-

ству

Итак, точка покоя с положительными координатами (что соответствует сосуществованию жертв и хищников) будет лишь в том случае, когда емкость среды для жертв будет больше, чем емкость среды для хищников, т.е. популяция жертвы должна быть достаточной для того, чтобы прокормить хищников.

Исследуем характер точки покоя :

33

так как выполнены условия (2.10), а TrW kc 0. d

В силу критерия асимптотической устойчивости для систем 2-го порядка исследуемая неподвижная точка устойчива.

Согласно (2.5)

Видим, что дискриминант D может быть как положительным, так и равным нулю и отрицательным. В зависимости от знака D движения системы

спирали, в случае D < 0 (т.е. положение равновесия – устойчивый фокус, а колебания системы затухают, и процесс становится стационарным), либо, в случае D 0, исследуемая точка покоя – устойчивый узел, т.е. колебания отсутствуют. Таким образом, введение члена -kN12 в уравнение для жертвы при выполнении условий (2.10) ведет к затуханию колебаний системы.

Знак дискриминанта D зависит от соотношений параметров a,b,c,d и k. Для определения этих соотношений обозначим k/d = r, a/c = s . Тогда

D = c2[(r + 2)2 - 4(1+ s)].

Из сказанного выше следует, что исследуемое положение равновесия будет устойчивым фокусом, если

D 0 ;

(2.11)

0 r s

это условие (2.10).

Положение равновесия будет устойчивым узлом, если

D 0;

(2.12)

0 r s.

В системе координат r,s построим график функции D = 0 (рис.2.17).

34

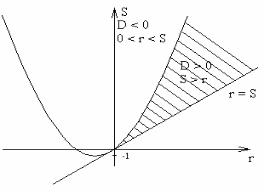
На рис. 2.17 парабола – это то множество точек (r,s), для которых выполняется условие D = 0. Вне параболы D > 0, а внутри параболы D<0. Для точек из заштрихованной области выполнены условия (2.12), а для точек той части внутренности параболы, которая лежит в 1-м октанте, выполнены условия (2.11).

Рис. 2.17. График функции дискриминанта D

УПРАЖНЕНИЕ 3. Есть ли еще неподвижные точки для системы

Если есть, то исследовать их характер и дать экологическую интерпретацию.

2.2.2.3. Рассмотрим следующую модель "хищник – жертва" с наличием убежища (модель 2в).

Предположим, что к условиям задачи (2.8) добавлено условие, что часть особей жертвы может найти убежище, укрытие от хищника. Система уравнений в этом случае будет иметь вид

где Nr < N1 – число особей жертвы, нашедших убежище.

УПРАЖНЕНИЕ 4. Предполагается самостоятельно провести исследование динамики решения системы (2.8) в случаях, когда :

а) Nr = kN1, т.е. численность жертвы, находящей убежище, составляет некую постоянную долю ее общей численности;

б) Nr = const , т.е. численность жертвы, находящей убежище, посто-

янна.

2.2.2.4. Рассмотрим следующую модель "хищник – жертва" с изъятием части популяции (модель 2г).

Модель 2г получается такой модификацией задачи (2.8): к каждому уравнению для Ni добавляется член - iNi , который соответствует изъятию части популяции ("сбору урожая"). Такие члены возникают, например, при

35

описании влияния рыболовства на популяции рыб или инсектицидов при изучении популяции насекомых.

Система уравнений в этом случае будет иметь вид

2.2.3. Модели распространения эпидемий (модели 3а,3б)

Рассмотрим популяцию, в которой распространяется болезнь. Пусть N

– численность популяции, постоянная величина. Считаем, что заражение происходит при непосредственном контакте больных и здоровых и смертность отсутствует.

2.2.3.1. Рассмотрим математическую модель эпидемии болезни без иммунитета (модель 3а). Популяция состоит из двух групп: здоровые (N1) и больные (N2). Если Z(N1,N1) и V(N1,N1) – скорость заражения и выздоровления соответственно, то систему уравнений можно записать в виде

N N1 N2 .

Положим, что все больные разбиты на две группы – больных, но невыявленных, выявленных и изолированных, т.е. не допускаемых к контакту. Пусть – доля больных, выявляемых органами здравоохранения за единицу времени. Тогда в контакт могут вступать (1- )N2 больных и N1 здоровых. За единицу времени выберем Т– время изоляции больных (время излечения). Считаем, что здоровый человек может заразиться с вероятностью, пропорциональной доле заболевших среди всех, допущенных к контакту. Итак, в единицу времени может заразиться столько человек:

Z (1 )N1N2 . N1 (1 )N2

Здесь – количество контактов в единицу времени в расчете на особь. Теперь опишем скорость выздоровления V (число излеченных в единицу времени). Cчитая, что все заболевшие излечиваются, получаем, что V = = N2, т.е. в выбранную единицу времени излечиваются N2 особей. С другой стороны, скорость выздоровления зависит и от стратегии обнаружения заболевших. Предположим, что относительно этой стратегии выполнены следующие гипотезы:

36

1)имеется определенная доля заболевших D, самостоятельно обращающихся к врачу;

2)органами здравоохранения проводится профилактическая проверка населения на предмет выявления заболевания. Если в единицу времени обследуется А особей, то считаем, что число обнаруженных больных среди них равно АN2/N (пропорционально доле заболевших);

3)предполагаем, что каждый из выявленных указал еще на С больных, бывших с ним в контакте.

Тогда V = C(DN2 + АN2/N)= N2 – число выявленных больных в единицу времени. Если С=2 , то = 2( D + A/N ).

Найдем неподвижные точки для системы (2.14). Условием неподвижности будет равенство Z = V .

Очевидно, что точка (0,0) является неподвижной точкой.

(1- )N1 = ( N1 +(1- )N2);

(1 )N

N1 2 .

Отсюда видим, что неподвижными будут все точки, лежащие на прямой, для которых выполнено условие N1 + N2 = N.

На рис.2.18 точка А является искомой нетривиальной неподвижной точкой для системы (2.14).

Рис. 2.18.Положение искомой нетривиальной точки для исследуемой системы

37

Заметим, что должно быть выполнено неравенство - - 2 > 0, иначе прямая

(1 )N N1 2

будет лежать в левой полуплоскости и единственным положением равновесия по смыслу нашей задачи будет лишь начало координат.

Таким образом, точка А (нетривиальное положение равновесия) будет иметь положительные координаты, что необходимо для нашей задачи, если выполнено условие - - 2 > 0; отсюда получаем

В [1] указано, что при выполнении этого условия положение

1 N N1 2

равновесия (0,0) будет неустойчивым (что соответствует распространению

эпидемии), а положение равновесия А – устойчивым.

Если же

то единственным положением равновесия будет начало координат, причем устойчивым. Таким образом, при выполнении этого условия эпидемии не возникнет.

Число контактов в единицу времени зависит от конкретной болезни и определяется для каждой болезни по статистическим данным. Например, в случае распространения венерических заболеваний или СПИДа, по данным США, = 8,5 контактов в месяц в расчете на особь.

ПРИМЕР. Предположим, что в некоторой популяции распространяется заболевание. Пусть = 8,5 в месяц, 30 заболевших обращается к врачу (т.е. D = 0,3). Считаем также, что каждый выявленный больной назовет

38

хотя бы одного заболевшего (т.е. С = 2). Какой процент популяции должен быть обследован, чтобы не возникло эпидемии ?

Т.к. в нашем примере = 2·(0,3 + A/N) , то для предотвращения эпидемий должно выполняться условие 2(0,3 + A/N) > 8,5/9,5, отсюда получаем А>0,15, т.е. эпидемии не возникнет, если будет обследовано в единицу времени около 15 всей популяции.

2.2.3.2.Далее рассмотрим математическую модель эпидемии болезни

симмунитетом (модель 3б). Пусть теперь среди популяции распространяется болезнь, оставляющая после себя стойкий иммунитет. Тогда популяция состоит из трех групп: здоровые, но подверженные инфекции (N1), больные (N2) и здоровые, но уже переболевшие болезнью, т.е. с приобретенным иммунитетом (N3). В этом случае система для описания распространения будет иметь вид

N N1 N2 Nз.

Начальные условия для этой задачи:

N1(0)= N10 , N2(0)= N20 , Nз(0)= 0.

Здесь скорость заражения V(N1,N2) = rN1N2, где r – коэффициент заражения. Скорость выздоровления W(N1,N2) = sN2 , где s – коэффициент выздоровления, показывающий, какая доля из заболевших выздоровела и приобрела иммунитет.

Заметим, что в данном случае система не имеет неподвижных точек. Поэтому та теория, которая использовалась до сих пор, неприменима. Для проведения исследования динамики системы найдем решение системы.

dt

39

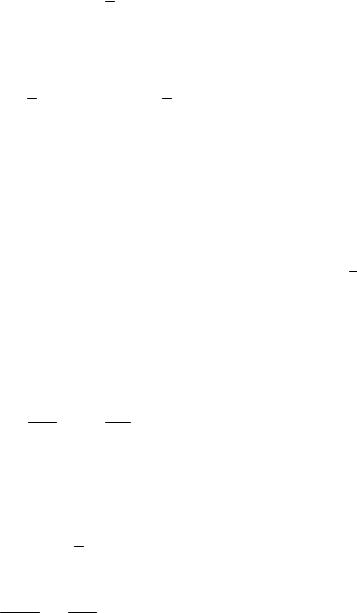
Получаем уравнение с разделяющимися переменными:

где С – произвольная постоянная.

Решение задачи Коши для системы (2.11) получим, выразив из последнего уравнения константу С для данных начальных условий.

С N20 N10 s LnN10 .

r

Отсюда решение исходной задачи:

N2 N1 s LnN1 N20 N10 s LnN10 . r r

Так как при t = 0 , N10 + N20 = N , получаем

Рассматривая поведение функции N2 при разных соотношениях для s , r

можем видеть, как меняется число заболевших.

Изобразим в фазовой плоскости N1, N2 интегральную кривую (2.16), т.е. изобразим ту кривую из фазового портрета системы (2.15), которая удовлетворяет начальным условиям задачи. Для построения продифференцируем уравнение (2.16) по N1.

dN2 1 s . dN1 rN1

Рассматривая N2 как функцию от N1, найдем точки экстремума этой функции. Необходимое условие для существования экстремума функции – это равенство нулю производной функции . Производная равна 0 при

s N1 r .

Вторая производная

2

d N2 s 0, dN12 rN12

40