Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1312.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

1.05 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

Таблица 21

Наиболее достоверные значения трех горизонтальных углов и их СКП

Угол	β
I–777–10	18°51′47,5″±13,2″
10–777–11	7°49′39″±13,2″
I–777–11	26°41′13,35″±13,2″

В итоге получили, что СКП не удовлетворяет паспортными данными электронного тахеометра Nikon Nivo5.С. Это несоответствие получено из-за того, что оценка точности выполнена по измерениям углов на коротких расстояниях, также было сделано относительно мало измерений. Можно предположить, что, увеличив расстояние, методи-

ку измерений и количество приёмов, можно достичь паспортной СКП
		И
измерения горизонтального угла одним полным приёмом электрон-
ным тахеометром.		Д
6. НАИБОЛЕЕ ДОСТОВЕРНАЯ ОЦЕНКА ТОЧНОСТИ
ИЗМЕРЕНИЙ УГЛОВ, ПОЛУЧЕННЫХ ТЕОДОЛИТОМ
Для углов, измеренных теодолитом, эти же углы, измеренные
	б
электронным тахеометром, являются истинными значениями. Таким

образом, возьмём для трёх рядов углов, измеренных теодолитом, со-
ответствующие средн е углы, измеренныеА	электронным тахеометром

в качестве истинныхизначений. Рассчитаем СКП измерения угла теодолитом 2Т30ПСпо формуле Гаусса.

6.1. Подготовка данных для нахождения истинной погрешности горизонтального угла, полученного по многократным измерениям теодолитом

Объединить в ряд одни и те же углы, измеренные теодолитом при разных высотах инструмента, и принять для них истинные значения соответствующего угла, полученные после обработки измерений электронным тахеометром.

Истинные значения трех горизонтальных углов:

β«I–777–10» = 18°51′47,5″;

β«10–777–11» = 7°49′39″;

β«I–777–11» = 26°41′13,35″.

Чтобы удобнее было обрабатывать данные, составим	табл.
22 – 25: для первого угла β«I–777–10», для второго угла β«10–777–11»	и для

третьего угла β«I–777–11» .

Затем по формуле Гаусса (20) находим СКП измеренного угла одним полным приемом теодолитом.

Таблица 22

Сравнение результатов измерения первого угла «I–777–10», полученных теодолитом, с истинным значением угла, полученным электронным тахеометром

№ п/п		Результат			∆	∆2
1		18°51′00″			-47,5″	2256,25″
2		18°51′00″			-47,5″	2256,25″
3		18°50′00″			-107,5″	11556,25″
4		18°50′30″			-77,5″	6006,25″
5		18°51′00″			И	2256,25″
5		18°51′00″			-47,5″	2256,25″
6		18°50′30″			-77,5″	6006,25″
7		18°50′30″			-77,5″	6006,25″
8		18°50′30″			-77,5″	6006,25″
9		18°51′00″			-47,5″	2256,25″
			А
10		18°51′00″			-47,5″	2256,25″
11		18°50′30″			-77,5″	6006,25″
12		18°50′30″			-77,5″	6006,25″
				Д
13		18°50′00″		-107,5″		11556,25″
14		18°51′30″			-17,5″	306,25″
		и
15		18°51′30″			-17,5″	306,25″
16		18°51′00″			-47,5″	2256,25″
17		18°51′00″			-47,5″	2256,25″
18	С				-77,5″	6006,25″
18		18°50б′30″			-77,5″	6006,25″
19		18°50′30″			-77,5″	6006,25″
20		18°50′30″			-77,5″	6006,25″
		β = 18°51′47,5″				Ʃ = 93575″

Таблица 23

Сравнение результатов измерения второго угла «10–777–11», полученных теодолитом, с истинным значением угла, полученным электронным тахеометром

№ п/п	Результат	∆	∆2
1	2	3	4
1	7°49′30″	-9″	81″
2	7°49′00″	-39″	1521″
3	7°50′00″	21″	441″
4	7°49′00″	-39″	1521″
5	7°50′00″	21″	441″
6	7°49′30″	-9″	81″

							Окончание табл. 23

1			2			3	4
7		7°50′00″				21″	441″
8		7°49′00″				-39″	1521″
49		7°49′00″				-39″	1521″
10		7°50′00″				21″	441″
11		7°49′30″				-9″	81″
12		7°49′30″				-9″	81″
13		7°50′00″				21″	441″
14		7°50′00″				21″	441″
15		7°50′30″				51″	2601″
16		7°50′00″				21″	441″
17		7°49′30″				-9″	81″
18		7°50′00″				21″	441″
19		7°50′30″				51″	2601″
						И
20		7°50′00″				21″	441″
		β = 7°49′39″				Ʃ = 90″	Ʃ = 15660″
					Д		2
							Таблица 24
Сравнение результатов измерения третьего угла «I–777–11», полученных
				А
теодолитом, с истинным значением угла, полученным электронным
			тахеометром
			б
№ п/п		Результат				∆	∆
1	26°40´30´´					-43,35´´	1879,22´´
2	26°40´00´´					-73,35´´	5380,22´´
3	26°40´30´´					-43,35´´	1879,22´´
	С
4	26°40´00´´					-73,35´´	5380,22´´
5	26°41´00´´					-13,35´´	178,22´´
6	26°40´30´´					-43,35´´	1879,22´´
		и
7		26°41´00´´				-13,35´´	178,22´´
8	26°40´30´´					-43,35´´	1879,22´´
9	26°40´30´´					-43,35´´	1879,22´´
10	26°40´00´´					-73,35´´	5380,22´´
11	26°41´30´´					16,65´´	277,22´´
12	26°40´30´´					-43,35´´	1879,22´´
13	26°40´00´´					-73,35´´	5380,22´´
14	26°41´00´´					-13,35´´	178,22´´
15	26°40´30´´					-43,35´´	1879,22´´
16	26°40´00´´					-73,35´´	5380,22´´
17	26°40´30´´					-43,35´´	1879,22´´
18	26°40´00´´					-73,35´´	5380,22´´
19	26°40´30´´					-43,35´´	1879,22´´
20	26°40´30´´					-43,35´´	1879,22´´
		β=26°41´13,35´´					Ʃ=51885,45´´

Таблица 25

Сводная таблица СКП измеренного угла по истинным погрешностям

Угол	β	m
β«I–777–10»	18°51′47,5″	68″
β«10–777–11»	7°49′39″	27,9″
β«I–777–11»	26°41′13,35″	51″

В итоге получили, что все полученные СКП не удовлетворяют паспортными данным теодолита 2Т30П из-за короткого расстояния между прибором и изменяемой точкой. В рядах измерений присутст-

вует систематическая погрешность. Можно предложить, что система- И

тическая погрешность возникла из-за неточного центрирования теодолита на станции.

6.2. Статистическое исследование вариационного ряда истинных погрешностей

Получены 60 значений истинных погрешностей измерения угла
теодолитом 2Т30П.		Д
Рассмотрение и осмысление этих данных (особенно при боль-
	и
шом числе наблюдений n) затруднительноА			, по ним практически нель-
зя представить характер распределения признака (случайной величи-
ны X).	б

	С				Таблица 26
	Ранжированный ряд в порядке возрастания

№ п/п	∆	№ п/п	∆	№ п/п	∆
1	2	3	4	5	6
1	-107,5	21	-47,5	41	-13,35
2	-107,5	22	-47,5	42	-13,35
3	-77,5	23	-47,5	43	-13,35
4	-77,5	24	-47,5	44	-9
5	-77,5	25	-43,35	45	-9
6	-77,5	26	-43,35	46	-9
7	-77,5	27	-43,35	47	-9

Первый шаг к осмыслен ю имеющегося статистического мате-

риала – это его упорядочение, расположение вариантов в порядке возрастания, т.е. ранжирование вариантов ряда (табл. 26).

Окончание табл. 26

1	2	3	4		5	6
8	-77,5	28	-43,35		48	-9
9	-77,5	29	-43,35		49	16,65
10	-77,5	30	-43,35		50	21
11	-77,5	31	-43,35		51	21
12	-73,35	32	-43,35		52	21
13	-73,35	33	-43,35		53	21
14	-73,35	34	-43,35		54	21
15	-73,35	35	-39		55	21
16	-73,35	36	-39		56	21
17	-73,35	37	-39		57	21
18	-47,5	38	-39		58	21
19	-47,5	39	-17,5	И		51
19	-47,5	39	-17,5	59		51
20	-47,5	40	-17,5		60	51

В таком виде изучать выборку погрешностей горизонтальных углов тоже не очень удобно из-за обилия числовых данных. Поэтому разобьем варианты на отдельные интервалы, т.е. проведем их группировку.

Число интервалов m следует брать не очень большим, чтобы по-
	Д
сле группировки ряд был не громоздким и не очень малым, чтобы не
потерять особенности распределения признака.
Согласно формуле СтерджесаАрекомендуемое число интервалов
вычисляется по формуле
б
m = 1+ 3,3221 lg n ,
и

где n – количество вариантов ряда.
ВеличинаСинтервала вычисляется по формуле
k =	xmax − xmin	,
	1+ 3,3221 lg n

где xmax – наибольшее значение варианта ряда; xmin – наименьшее значение варианта ряда.

В нашем примере k = 23.

Сгруппированный ряд представим в виде табл. 27.

в интервале

	Сгруппированный ряд			Таблица 27
	Сгруппированный ряд

№ п/п	Интервал			Частота ni
1	[-110 ; -90]			2
2	[-90	;	-70]	15
3	[-70	;	-50]	0
4	[-50	;	-30]	21
5	[-30	;	-10]	5
6	[-10	;	10]	5
7	[10	;	30]	10
8	[30	;	50]	0
9	[50	;	70]	2
				Ʃ = 60

Числа, показывающие, сколько раз встречаются варианты из данного интервала, называются частотами (обозначаем ni).

Графическое изображение вариационного ряда осуществим с помощью гистограммы. Гистограмма представляет собой ступенча-

тую фигуру из прямоугольников с основаниями, равными интервалам
значений признака:								И
значений признака:
		k	i	= x	i+1	− x , i = 1, 2,…,m,
			i		i+1		i Д
где xi – значение интервала признака;
xi+1					А
xi+1	– последующее значен е интервала признака.
Высота каждой ступени г стограммы равняется частоте интер-
вала.		б
вала.
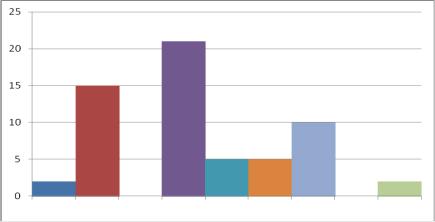
Гистограмма представлена на рис. 4.
	и
	С

Числопогрешностей	-90	-70	-50	-30	-10	10	30	50	70
-110

Статистические интервалы вариационного ряда, уг. с

Рис. 4. Гистограмма вариационного ряда

Вид гистограммы свидетельствует о том, что исследуемая нами выборка не соответствует нормальному закону распределения.

Видно значительно большую, чем у соседних, частоту для четвертого интервала и необоснованные провалы (нулевые частоты) в середине ряда. В рядах измерений присутствует значительная систематическая погрешность измерений: 48 значений из 60-ти имеют знак «минус», а это 80% от всех измерений. В соответствии с одним из свойств случайных погрешностей положительных и отрицательных погрешностей должно быть поровну. Можно считать, что полученные результаты не подчиняются закону нормального распределения. Для подтверждения этого утверждения выполним соответствующие расчеты.

							И
	6.3. Расчет статистических характеристик вариационного ряда
				истинных погрешностей
			Средние величины характеризуют значения признака, вокруг
которого концентрируются наблюдения, или, как говорят, централь-
ную тенденцию распределения. Наиболее распространенной из сред-
них величин является среднее арифметическое.
			Наиболее точно соответствие нормальномуД					закону распределе-
ния выборки будет характеризовать значение критерия Пирсона.
			Для вариационного рядаАнеобходимо рассчитать следующие
характеристики: среднее ар фметическое x , дисперсию S2, среднее
квадратическое отклоненбе σ (табл. 28).
			Средней арифмет ческой вариационного ряда называется сумма
произведений всех вариантови					на соответствующие частоты, деленная
на сумму частот:
			С		x =	[x n]	;
					x =	[n]	;
x =			(−100 2) + (−80 15) + (−60 0) + (−40 21) + (−20 5) + (0 5) + (20 10)						+
		(40 0)+ (60 2)				60
+		(40 0)+ (60 2)		′
				′
			60	= −34,8 .
			60

Дисперсией вариационного ряда называется среднее арифметическое квадратов отклонений вариантов от их средней арифметической:

S 2 =

[(xi

−)2 n];

[n]

(−100 + 34,8) 2 + (− 80 + 34,8) 15 + (− 60

+ 34,8) 0

+ ...

(20 + 34,8) 2 + (40 + 34,8) 0 + (60

+ 34,8) 2

′′

= 1475,5 .

Среднее квадратическое отклонение σ – арифметическое значе-

ние корня квадратного из дисперсии:

σ =

;

′′

= 1475,5

= 38,41 .

Таблица 28

Основные характеристики исследуемогоДвариационного ряда

-34, 8″

1475,5″

38,41″

6.4. ПодборкаСтеорет ческого распределения для эмпирического

распределения истинных погрешностей измерения горизонтального угла одним полным приемом теодолитом

Среди законов распределения непрерывных случайных величин наиболее распространенным является нормальный закон распределения. Случайная величина распределена по нормальному закону распределения, если ее плотность вероятности имеет вид

f (x) =		1		e−	(x− x )2
		1			2σ2 ,

	σ	2	π
	σ	2	π

где x – математическое ожидание случайной величины; σ – среднее квадратическое отклонение.

В этом случае говорят, что случайная величина подчинена нормальному закону распределения (это распределение также называют законом Гаусса).

Определение критерия χ2. Для расчета вероятностей pi попадания случайной величины X в интервал [xi, xi+1] используем функцию Лапласа в соответствии со свойством нормального распределения:

) =

- x

≤ X ≤ x

i+1

− Ф

i+1

где xi , xi+1– интервалы ряда;

x – среднее арифметическое;

σ– среднее квадратическое отклонение.

Чтобы найти значение функции Лапласа (табл. 29) по известно-

му значению аргумента, воспользуемся таблицей Лапласа (прил. 6).

					1			90			Д
pi (−110	≤ X ≤ −90) =				1			90	− (- 34,8)				-110 − (- 34,8)			= 0,05.
pi (−110	≤ X ≤ −90) =				2		Ф		38,4				− Ф	38,4		= 0,05.
					2				38,4					38,4
									А
							б								Таблица 29
							б
				Нахожден е функции Лапласа
				и
Номер		Интервал												Ф i+1	Ф i		pi
интервала		Интервал				Частота				Арг. i+1			Арг. i	Ф i+1	Ф i		pi
1		[-110 ; -90]						2		-1,44			-1,96	-0,850	-0,950		0,050
		С
2		[-90 ; -70]						15		-0,92			-1,44	-0,642	-0,850		0,103
3		[-70 ; -50]						0		-0,40			-0,92	-0,310	-0,642		0,165
4		[-50 ; -30]						21		0,12			-0,40	0,095	-0,310		0,203
5		[-30 ; -10]						5		0,65			0,12	0,484	0,095		0,194
6		[-10	;	10]				5		1,17			0,65	0,758	0,484		0,136
7		[10	;	30]				10		1,69			1,17	0,909	0,758		0,075
8		[30	;	50]				0		2,21			1,69	0,972	0,909		0,032
9		[50	;	70]				2		2,73			2,21	0,993	0,972		0,010
Для определения статистики χ 2												удобно составить табл. 30.

В таблице Лапласа находим значения Ф. Для начала по верти-

кали находим целые и десятые доли значения числа. Найдя в таблице значения, смотрим по горизонтали сотые доли значения числа.

					Определение статистики χ 2					Таблица 30
					Определение статистики χ 2

№		Интервал			Эмпириче-		Вероят-	Теорети-	(ni- npi)2	(ni − npi )2
п/п					ские час-		ности pi	ческие	(ni- npi)2	npi
					тоты ni			частоты		npi
								npi
1		[-110 ; -90]			2		0,050	2,997	0,994	0,331
2		[-90 ; -70]			15		0,103	6,231	76,895	12,340
3		[-70 ; -50]			0		0,165	9,948	98,962	9,948
4		[-50 ; -30]			21		0,203	12,189	77,633	6,369
5		[-30 ; -10]			5		0,194	11,664	44,408	3,807
6		[-10	;	10]	5		0,136	8,211	10,310	1,255
7		[10	;	30]	10		0,075	4,530	29,92	6,605
8		[30	;	50]	0		0,032	1,917	3,674	1,917
9		[50	;	70]	2		0,010	0,624	1,893	3,034
					∑=60		∑=0,9719	∑=58,311		х2=45,61
		Таблица значений критерия Пирсона приведена в прил. 7.
							А
		Таким образом, фактическое наблюдаемоеИзначение статистики
χ	2 = 45,61.					б		Да нормальный закон распределе-
		Так как число интервалов m=9,						Да нормальный закон распределе-

ния определяется r = 2 параметрами, то число степеней свободы будет
и
С	k = m − r −1 = 9 − 2 −1 = 6.

Распределен е χ 2 даёт возможность оценить степень согласо-

ванности теоретического и статистического распределений. Для распределений χ 2 составлены специальные таблицы. Пользуясь этими

таблицами, можно для каждого значения χ 2 и числа степеней свободы найти вероятность того, что величина, распределенная по закону χ 2 , превзойдет это значение. Вероятность, определенная по таблице,

есть вероятность того, что за счет чисто случайных величин мера расхождения теоретического и статистического распределений будет не меньше, чем фактически наблюдаемое в данной серии опытов значе-

ние χ 2 . Если эта вероятность мала, то результат исследования следу-

ет считать противоречащим нулевой гипотезе H0 о том, что теоретическое и статистическое распределения случайной величины совпадают.

В нашем примере χ2пр > χтеор2 , значит, гипотеза о выбранном теоретическом нормальном законе не согласуется с опытными данными.

Для значений χ2 в нашей выборке не выполняется неравенство χпр2 < χтеор2 . Полученное значение χ2 , равное 45,61, не принадлежит

ни одному уровню значимости.

Критерий получился очень большой. При описанных условиях и методиках проведения измерениий это ожидаемый результат. Невоз-

можно подобрать критическое значения χ2 ни на одном уровне зна-

чимости. Ряд погрешностей измерений угла теодолитом не соответствует нормальному закону распределения.

Скорее всего, причины этого – некачественные измерения.

Следствие – систематические погрешности, присутствие грубых по-

грешностей измерений. Можно предположить, что они возникли из-за

нарушения методики измерений, из-за приборных погрешностей тео-
	Д
долита или электронного тахеометра, из-за промахов при взятии от-
счетов и наведении.	А

Таким образом, оценка точности по формулеИГаусса для выбор-

ки из 60-ти значений неприемлема. Оценка точности по формуле Га-

	б
усса предназначена для ряда случайных погрешностей. Если все-таки
в нашем примере её осуществить, достоверность будет низкая.
и
С

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.20211.05 Mб111308.pdf
#
07.01.20211.05 Mб11309.pdf
#
07.01.2021305.17 Кб0131.pdf
#
07.01.20211.05 Mб11310.pdf
#
07.01.20211.05 Mб11311.pdf
#
07.01.20211.05 Mб11312.pdf
#
07.01.20211.06 Mб01313.pdf
#
07.01.20211.06 Mб31314.pdf
#
07.01.20211.06 Mб21315.pdf
#
07.01.20211.06 Mб131316.pdf
#
07.01.20211.06 Mб181317.pdf