1263

решении задачи на компьютере. Построение модели это творческий процесс, требующий глубоких знаний и немалых способностей. Алгоритмы задач поиска оптимального решения достаточно сложны. Изложение методов решения (например, симплекс-метода) нам не понадобится, так как компьютер с помощью программного обеспечения MS Excel позволяет реализовать алгоритм поиска оптимального решения. Наша задача научиться строить математическую модель и пользоваться этим алгоритмом.

5.1. Общий случай задачи оптимизации

Процесс построения модели нужно начинать с ответа на следующие четыре вопроса:

1.Для каких величин строится модель, то есть каковы

переменные модели xj? Здесь j текущее значение переменных, общее количество которых равно n.

2.В чем состоит цель, для достижения которой из множества всех допустимых значений выбираются оптимальные? То есть надо

знать функцию цели (ЦФ целевая функция) или критерий

оптимизации

F= f(хj).

Критерий оптимизации (ЦФ) показывает, в каком смысле решение должно быть оптимальным. При этом возможны три вида назначения целевой функции:

максимизация;

минимизация;

назначение заданного значения.

3.Каким ограничениям должны удовлетворять неизвестные (ОГР)? Ограничения устанавливают зависимости между переменными. Они могут быть как односторонними

qi(xj) bi,

так и двусторонними

ai qi(xj) bi,

здесь i текущее значение зависимостей, общее количество которых равно m.

40

(целевая функция), по которому выбирается одно из допустимых решений.

5.2. Классификация математических моделей

Научный подход к любой проблеме это систематизация. Систематизация это классификация по ряду признаков.

Исходными данными для математической модели являются: целевая функция F(xj), левые q(xj) и правые bi части ограничений. Если значения исходных данных точно известны, то такие данные называются детерминированными. Если их значения заранее не определены, то эти данные являются случайными величинами.

Искомые переменные могут быть непрерывными и дискретными. Непрерывными называются такие величины, которые в заданных граничных условиях могут принимать любые значения. Дискретные принимают только заданные значения. Целочисленными называются такие дискретные переменные, которые могут принимать только целые значения.

Зависимости между переменными, как в целевой функции, так и в ограничениях, могут быть линейными и нелинейными. Линейными называются зависимости, в которых переменные входят в первой степени и с ними выполняются только действия сложения, вычитания и умножения на постоянный множитель. В противном случае зависимости являются нелинейными. При этом следует иметь в виду, что если в задаче хотя бы одна зависимость нелинейная, то и вся задача является нелинейной.

Сочетание различных элементов модели образуют различные классы задач оптимизации, которые требуют различных методов решения (табл. 3).

42

5.3. Задача распределения ресурсов

Если финансы, оборудование, сырье и даже людей полагать ресурсами, то значительную часть задач в экономике можно рассматривать как задачи распределения ресурсов. Как правило, это задачи линейного программирования.

Пример.

Пусть требуется определить, в каком количестве надо выпускать продукцию четырех типов, для изготовления которых требуются ресурсы трех видов (трудовые, сырье и финансы) с целью получения максимальной прибыли.

Первоначально для построения математической модели сформируем табл. 4, в которую будут входить: нормы расхода1; наличие располагаемого ресурса и прибыль в денежных единицах, полученная от реализации данного вида продукции.

Составим математическую модель, для чего введем следующие обозначения:

xj количество выпускаемой продукции j-го типа, j=1 4; bi количество располагаемого ресурса i-го вида, i=1 3;

aij норма расхода i го ресурса для выпуска единицы продукции j-го типа;

сj прибыль, получаемая от реализации единицы продукции j-го

типа.

Как видно из табл. 4, для выпуска единицы Прод1 требуется 5 единиц сырья, значит, для выпуска всей продукции Прод1 требуется 5x1 единиц сырья. С учетом того, что для других видов продукции зависимости аналогичны, ограничение по сырью будет иметь вид

5x1 + 6x2 + 4x3 + 3x4 110.

1 Количество ресурса каждого вида, необходимого для выпуска единицы продукции каждого типа, называется нормой расхода.

43

В этом ограничении левая часть равна величине потребного ресурса, а правая показывает количество имеющегося ресурса.

Аналогично можно составить ограничения для остальных ресурсов и написать зависимость для целевой функции. Тогда математическая модель задачи будет иметь вид

Алгоритм ввода данных и решения задачи линейного программирования в Excel.

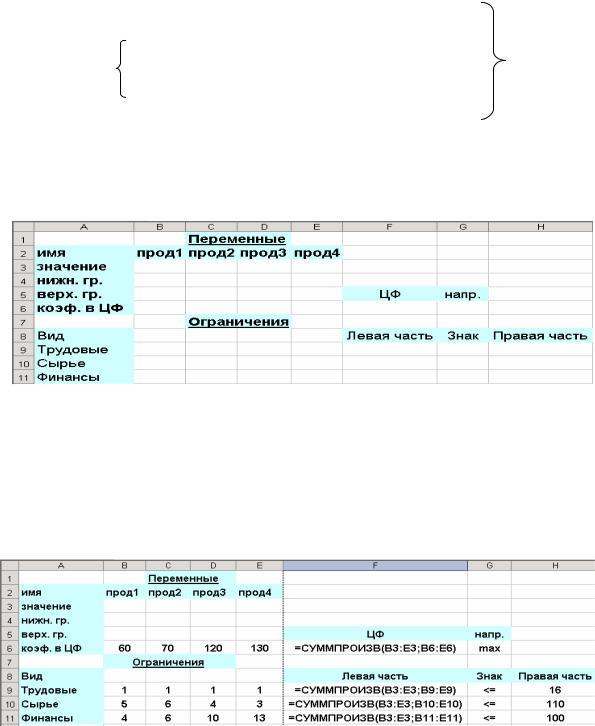
Ввести тексты (рис. 30).

Рис. 30. Текстовое оформление задачи в Excel

Весь текст на рис. 30 является комментарием и на решение задачи не влияет.

Вести в таблицу Excel зависимости из математической модели

(11) (рис. 31).

Рис. 31. Пример ввода математической модели оптимизации

44

Получим рис. 32.

Рис. 32. Результат ввода данных

Далее следуют команды Сервис Поиск решения (заполнить диалоговое окно рис. 33) Выполнить Ok.

Рис. 33. Пример заполнения окна Поиск решения

При планировании, например, выпуска ткани, бензина и т. д., величина выпускаемой продукции является дробной. При выпуске штучной продукции очевидно, что в плане должны быть целые числа. Для решения задачи целочисленного программирования в диалоговом

45

окне Поиск решения (см. рис. 33) следует добавить ограничение

(рис. 34).

Рис. 34. Окно добавления ограничений

На экране результат решения (рис. 35).

Рис. 35. Результат решения по условию задачи

Получено оптимальное решение для поставленной задачи, но до принятия управленческого решения еще далеко. Необходим всесторонний анализ полученного решения. Видов анализа существует много. Рассмотрим важнейшие из них (на наш взгляд обязательные).

46

5.4. Параметрический анализ

Параметрическим назовем анализ, который заключается в решении задачи при различных значениях некоторого параметра. Будем анализировать задачу распределения ресурсов, решая эту задачу при различных значениях имеющихся финансов, которые ограничивают улучшение целевой функции.

Заполним итоговую таблицу (рис. 36) для различных вариантов финансирования. Для этого в ячейку Н11 внесем значение = 50 и выполним пункт №3 алгоритма решения нашей задачи. После получения решения заполним ячейки В15:В22. Повторим алгоритм решения для остальных вариантов финансирования (Н11=100, 150, 200 и 250) с заполнением соответствующих ячеек итоговой таблицы.

Рис. 36. Пример составления итоговой таблицы

47

Из рис. 37 a, б, в можно сделать следующие выводы:

при различном финансировании в план входит продукция различных видов, однако ни в один вариант не входит выпуск продукции Прод2. Это объясняется тем, что при высоком потреблении ресурсов прибыль от ее производства ниже, чем от производства других видов продукции;

увеличение финансирования дает увеличение прибыли, что вполне естественно;

при увеличении финансирования, начиная со 150 ден. ед., происходит уменьшение потребляемого сырья. Такой результат является неожиданным, но это не ошибка. Это следствие того, что выпуск Прод3, Прод4, обеспечивающих увеличение прибыли, требует при этом

меньшего потребления сырья.

Данный параметрический анализ привел к выводу, который нас не устраивает, так как все продукты должны выпускаться, причем в определенном количестве (не ниже допустимого). В условии задачи ничего не сказано о том, в каких количествах должна выпускаться продукция. Поэтому необходимы дополнительные условия, которые, как правило, вытекают из маркетинговых исследований рынка сбыта. Предположим, что анализ рынка сбыта показал необходимость выпуска Прод2 2, а Прод4 4. Финансирование проекта примем = 150 ден. ед. (меньше не желательно, а больше невозможно). Тогда после выполнения соответствующего алгоритма в Excel получим (рис. 38).

Рис. 38. Оптимальный вариант при данных ограничениях

49