Фуккциям многих переменных. (2 семестр)

ЗАДАЧА № 1. Нахождение области определения функции сводится к решению неравенств с двумя неизвестными.

Разобрать на примере аналог метода интервалов

ПРИМЕР. Решить неравенство .

Решение.а) Определяем ОДЗ – пунктирная (запрещенная) гипербола. б) Неравенство превращаем в уравнение и строим соответствующую линию (сплошную, т.к. неравенство нестрогое). в) Вся плоскость разделилась линиями пунктов а) и б) на шесть областей. При помощи пробных точек выбираем из этих областей нужные и отмечаем их штриховкой.

Получающаяся картинка является ответом.

ПРИМЕР. Найти область определения функции .

В этом случае рассматриваем систему 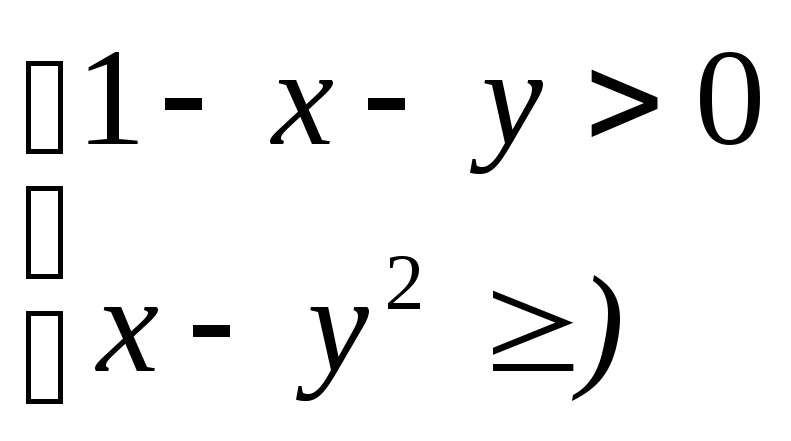, Решаем отдельно каждое неравенство и накладываем ответы друг на друга. Общая часть областей дает ответ.

Далее следует выяснить характеристики области определения:

замкнутость= граница принадлежит области определения;

ограничен­ность= область определения можно поместить в некоторый круг;

связность= любые две точки области определения можно соединить линией, не выходя за границы области определения.

Примечание. Областьюназывается связное открытое множество.Область определения функциине всегда являетсяобластью.

Эта задача решается вручную. MAPLE можно использовать, если есть желание, для построения кривых пунктов а) и б).

ЗАДАЧА № 4. Пусть требуется найти наибольшее и наименьшее значения функции z = x – 1/y в треугольнике А(2, 1) , В(4, 4) , С(6, 2). Для этого покроем область треугольника семейством линий уровня и выберем из этих уровней наибольший и наименьший.

Задаем два объекта: P – набор линий уровня. Некоторые проходят через вершины треугольника. Q – сам треугольник на плоскости. Обе команды заканчиваются двоеточием!!! Затем объединяем эти объекты командой display.

> with(plots):

> P:=contourplot(x-1/y,x=0..7,y=0..5,

contours=[1,2.4,3.75,4.5,5.5],color=black):

> Q:=PLOT(POLYGONS([[2,1],[4,4],[6,2]])):

> display({P,Q});

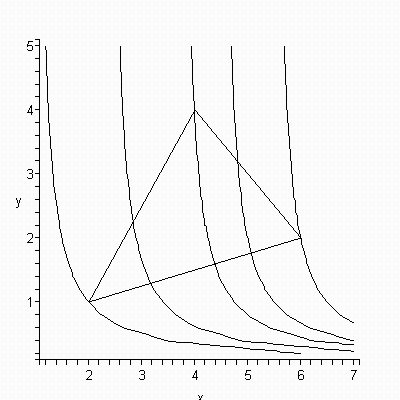
Ответ. Наибольшее значение функции равно 5,5 , Наименьшее равно 1.

ЗАДАЧА № 5. Решается полностью при помощи MAPLE .

ЗАДАЧА № 6 . Определение. Пусть функция z=f(x,y) имеет в точке (х,у) частные производные. Тогда дифференциалом этой функции на отрезке от точки A(x,y) до точки B(x+x, y+y) называется величина .

Примечание. При малых x и y величина dz  приращению z .

Пусть требуется вычислить величину z = . Эта величина равна

z= 5 + dz

Найдем дифференциал функции

Задаем функцию

> z:=sqrt(x^2+y^2);

Находим её дифференциал

> dz:=diff(z,x)*dx+diff(z,y)*dy;

Подставляем в него значения x=3, y=4. dx=0.007, dy= –0,005

> evalf(subs(x=3,y=4,dx=0.007,dy=-0.005,dz));

Ответ: z  5+dz = 5,0002

Найдем для проверки точное значение величины z

> sqrt(3.007^2+3.995^2);

ЗАДАЧА 7. Экстремум функции многих переменных.

Теорема. Пусть гладкая функцияz = f(x,y) имеет экстремум в точке(х₀ ,у₀) . Тогда в этой точке частные производные этой функции обращаются в ноль.

Другими словами, возможные точки экстремума можно найти, решая систему

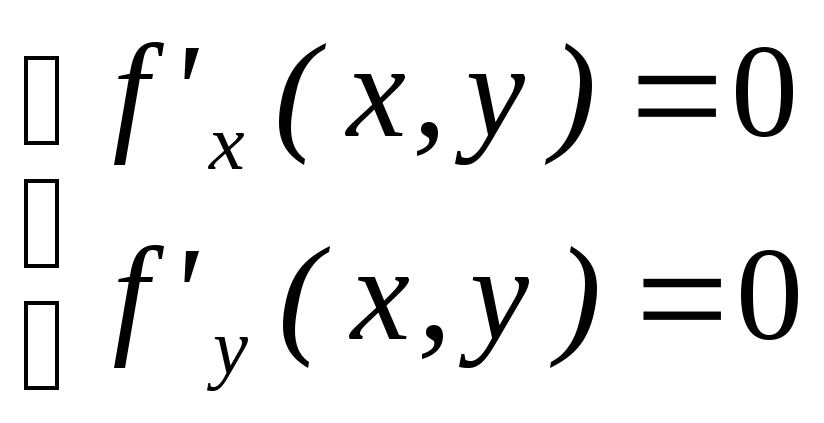
Решения этой системы называются критическими точками.

Задаем функцию

> z:=x^3+3*x*y^2-3*x;

_{и находим её критические точки, решая систему}

> solve({diff(z,x),diff(z,y)},{x,y});

_{Мы нашли четыре критические точки. Выясним, чем являются эти точки. Для этого в данной критической точке (х0 , у0) вычисляем вторые производные}

>A:=subs(x=x0,y=y0,diff(z,x,x));B:=subs(x=x0,y=y0,diff(z,x,y));C:=subs(x=x0,y=y0,diff(z,y,y));

а также величину

> d:=A*C-B^2;

_{Затем используем достаточные условия экстремума}

если d<0, то нет экстремума; если же d>0 и A>0, то имеется минимум; если же d>0 и A<0, то имеется максимум.

_{Эти условия следует оформить в виде программы:}

> if d<0 then print ('net*extr') elif d>0 and A>0 then print ('minimum') elif d>0 and A<0 then print ('maximum') end if;

Применяя эти условия, найдем: (–1, 0) – точка максимума, Z_max= 2 ,

(+1, 0) – точка минимума, Z_min= –2 .

Остальные точки не являются точками экстремума

Достаточные условия экстремума (геометрический метод).

Изобразим на плоскости XOY линию уровня z=0 нашей функции, используя команды

>with(plots):

>implicitplot(x^3+3*х*y^2-3*х,x=-2..2,

y=-2..2,thickness=3,color=black);

Линия уровня z=0 делит всю плоскость на четыре области. Определим знак функции в каждой из областей. Отметим на чертеже критические точки. Критическая точка (–1, 0) , лежащая на «холме», является точкой максимума. Соответственно точка (1, 0) попадает во «впадину». Это точка минимума. Критическая точка (0, 1) находится на линии уровня, и поэтому значение функции в этой точке равно нулю. Кроме того видно, что в любой малой окрестности этой точки наша функция принимает как

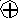
положительные, так и отрицательные значения. Поэтому эта точка не является ни точкой максимума, ни точкой минимума. Аналогичные рассуждения справедливы для точки (0,–1).

КОНТРОЛЬНАЯ РАБОТА ПО

КРАТНЫМ ИНТЕГРАЛАМ

1. Вычислить по области, ограниченной линиями

у =2 – 2х, у =2 – х, х = 1.

Решение. Строим данные линии. Затем полученную область записываем в правильном виде (Х– от числа до числа,Y– от линии до линии):

S=.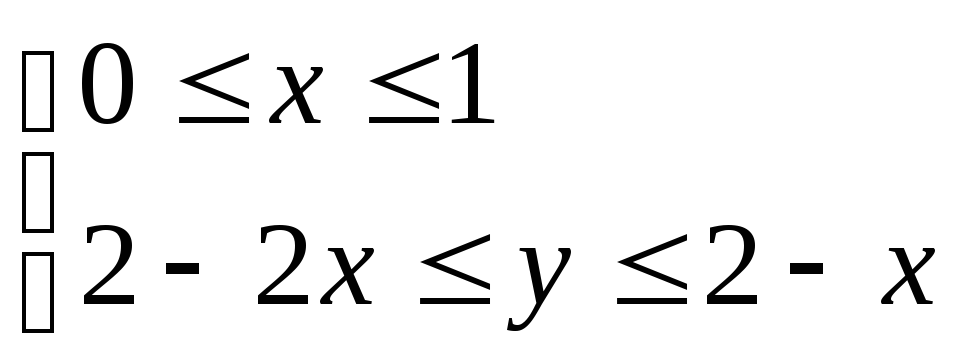

Соответственно этим неравенствам наш двойной интеграл превращается в повторный

.

2. Вычислить координаты центра тяжести области S.

Прежде всего находим площадь области по формуле . Затем находим координаты центра тяжести по формулам.

ПРОВЕРКА. Центр тяжести должен находиться внутри области треугольника.

3. Последняя задача решается также как и первая.

ДОМАШНЯЯ РАБОТА ПО ДВОЙНЫМ ИНТЕГРАЛАМ

(дополнении к контрольной)

Задача 1. Определить координаты центра тяжести области из домашней работы по определенным интегралам, задача № 2.

Решение. Пусть область S ограничена линиями у=, у=х–х²/4 , у=4 – х .

1. Строим кривые, находим точки пересечения и выясняем, что область S можно определить неравенствами 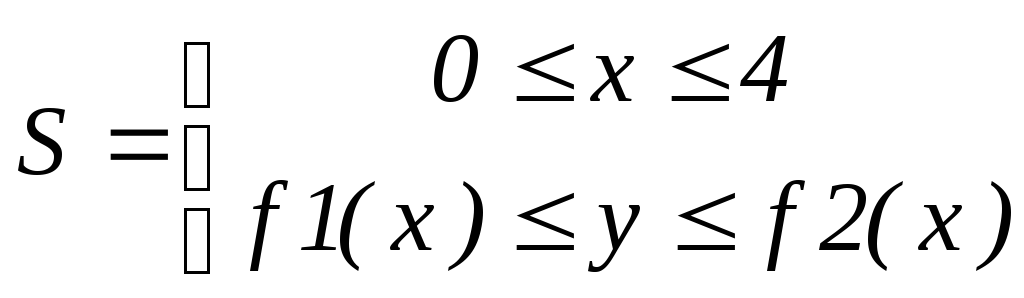, гдеf1(x) , f2(x) – нижняя и верхняя границы области, определяемые командами

> f1:=x->x-x^2/4; f2:=x->piecewise(x<=2,sqrt(2*x),4-x);

Для контроля полезно построить область S (на этот рисунок мы будем в дальнейшем наносить центр тяжести).

> plot({f1(x),f2(x)},x=0..4,color=black);

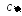
2. Определяем площадь области по формуле . Этот двойной интеграл следует ВРУЧНУЮ свести к повторному , и только затем вычислить при помощи MAPLE

> S:=int(int(1,y=f1(x)..f2(x)),x=0..4);

S:=2

3. Определяем иксовую координату центра тяжести фигуры S: . Этот двойной интеграл следует свести к повторному вручную , а затем вычислить при помощи MAPLE

> Xc:=1/S*int(int(x,y=f1(x)..f2(x)),x=0..4);

4. Аналогичным образом находим вторую координату центра тяжести

> Yc:=1/S*int(int(y,y=f1(x)..f2(x)),x=0..4);

5. Отметить центр тяжести на фигуре S.

КОНТРОЛЬ. Для выпуклых фигур центр тяжести должен находиться внутри области S!!!

Задача 2. Вычислить при помощи двойного интеграла ОБЪЕМ усеченной призмы из домашней работы по определенным интегралам (задача № 3).

Решение. По геометрическому смыслу двойного интеграла искомый объем равен

где плоскость z=A+Bx+Cy ограничивает призму сверху, а S – это область, на которую призма опирается.

ДОМАШНЯЯ РАБОТА ПО

ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ

Из вариантов решаются задачи 2, 3, 4.

ЗАДАЧА 2. Задача Коши – это задача нахождения функции, удовлетворяющей дифференциальному уравнению и заданным начальным условиям.

Задача Коши решается ВРУЧНУЮ по инструкции:

А) Находим общее решение ЛОУ (линейного однородного уравнения)

:

Для этого составляем характеристическое уравнение a ² + b + c = 0 и находим его корни. Возможны следующие случаи:

а) Дискриминант > 0 . Два различных корня ₁= А , ₂ = В . Общее решение ЛОУ имеет вид

.

б) Дискриминант = 0. Два одинаковых корня  ₁ =  ₂ = А. Общее решение ЛОУ имеет вид

в) Дискриминант < 0. Два комплексных корня  _1,2 = А  Вi. Общее решение ЛОУ имеет вид

.

Здесь всюду С₁ иС₂ –произвольные константы.

Б) Используя начальные условия y(0)=a , y’(0)=b , находим значения произвольных константС₁ иС₂ и подставляем эти значения в общее решение.

В) Обязательно пишем следующее: «ОТВЕТ: Решение задачи Коши, т.е. функция, удовлетворяющая уравнению и начальным условиям, имеет вид …».

Примечание. Обязательно проверьте своё «ручное» решение на MAPLE.

ЗАДАЧИ 3 и 4. В этих задачах приведены линейные неоднородные уравнения (ЛНУ). Каждое из этих уравнений нужно дополнить нулевыми начальными условиями y(0)=y’(0)=0 и решить при помощиMAPLE две получившиеся задачи Коши. Метод решения задачи Коши разобрать самостоятельно по инструкции дляMAPLE, раздел «Дифференциальные уравнения». Построить график каждого из полученных решений на отрезке[0; 1] .