
1022
.pdf
В. Н. Завьялов, В. М. Романовский
ОБЪЁМНАЯ И ПЛОСКАЯ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Учебно-методическоепособие
B |
|
P |
|
y |
|
|
|
|
P |
|
Px |
M |
|
|
C |
Pz |
|
A 
Омск 2014
Министерство образования и науки РФ Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования «Сибирская государственная автомобильно-дорожная академия (СибАДИ)»
В. Н. Завьялов, В. М. Романовский
ОБЪЁМНАЯ И ПЛОСКАЯ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Учебно-методическое пособие
Омск
СибАДИ
2014
УДК 624+539.3 ББК 38.112 З93
Рецензенты:
канд. техн. наук, доц. О. Н. Попов (ТГСАУ) д-р техн. наук, проф. В. Н. Шестаков (СибАДИ)
Работа одобрена редакционно-издательским советом ФГБОУ ВПО «СибАДИ» в качестве учебно-методического пособия.
Завьялов, В. Н.
З93 Объёмная и плоская задачи теории упругости : учебно-методическое пособие / В. Н. Завьялов, В. М. Романовский. – Омск : СибАДИ, 2014. – 56 с.
ISBN 978-5-93204-699-9
Изложены основы теории упругости, связанные с исследованием напря- жённо-деформированного состояния в точке упругого тела и решением задачи плоского напряжённого состояния – расчёта балки-стенки. Кроме того, в пособии представлены примеры выполнения расчётно-графических работ, задания и схемы рассчитываемых балок-стенок.
Адресовано студентам, обучающимся по строительным направлениям и специальностям, а также магистрантам, занимающимся исследованием работы строительных конструкций зданий и транспортных сооружений.
УДК 624+539.3 ББК 38.112
ISBN 978-5-93204-699-9 |
© ФГБОУ ВПО «СибАДИ», 2014 |
Оглавление
Введение………………………………………………………………......4
1. Исследование напряжённо-деформированного состояния в точке упругого тела
при известном тензоре напряжений…………………………………..…4
Контрольные вопросы…………………………………………………..14
2. Числовой пример исследования напряжённо-деформированного состояния в точке упругого тела
при известном тензоре напряжений...........…………………………….14
3. Плоская задача теории упругости. Балка-стенка……………………24
Контрольные вопросы…………………………………………………..33
4. Пример расчёта балки-стенки.....…………………………………….33
Библиографический список……………………………………………..55
3
ВВЕДЕНИЕ
Настоящее учебно-методическое пособие написано на основе курса лекций и практических занятий, читаемых и проводимых авторами студентам строительных специальностей.
Теория упругости представляет собой раздел механики деформируемого твёрдого тела, изучающий работу твёрдого тела, материал которого является идеально упругим, находящимся под воздействием внешних силовых факторов [2, 4, 7].
Аналогичные задачи рассматриваются и в разделе механики деформируемого твёрдого тела – сопротивлении материалов. Однако между теорией упругости и сопротивлением материалов имеются существенные различия, связанные с принятием исходных предпосылок и соответственно им методов расчёта.
Всопротивлении материалов рассматриваются приближённые теоретические методы, связанные с принятием большого количества упрощающих гипотез и предпосылок.
Теория упругости при решении задач использует меньшее число упрощающих гипотез и предпосылок. Так, в ней отсутствует одна из основных гипотез сопротивления материалов – гипотеза плоских сечений.
Вэтой связи теория упругости отличается большей широтой методов расчёта, а сами методы отличаются большей математической строгостью и сложностью.
Втеории упругости рассматриваются задачи, которые не могут быть решены методами сопротивления материалов. Кроме того, аппарат теории упругости позволяет дать оценку точности решения задач, рассматриваемых в сопротивлении материалов.
Рассматриваемые в настоящем учебно-методическом пособии задачи относятся к классической (линейной) теории упругости – исследование напряжённо-деформированного состояни в точке упругого тела и плоская задача теории упругости (плоское напряжённое состояние).
1.ИССЛЕДОВАНИЕ НАПРЯЖЁННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ В ТОЧКЕ УПРУГОГО ТЕЛА
ПРИ ИЗВЕСТНОМ ТЕНЗОРЕ НАПРЯЖЕНИЙ
Прежде чем рассматривать напряжённо-деформированное состояние в точке упругого тела, представим теоретические обоснования, необходимые для такого исследования.
4
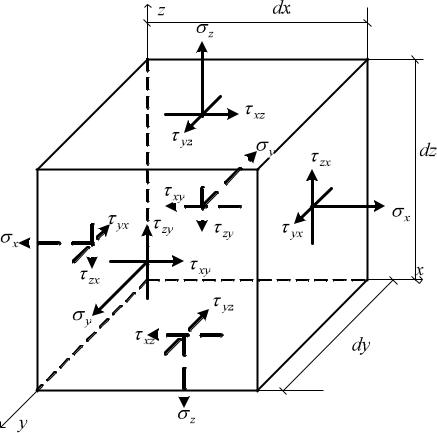
Известно, что при физическом воздействии на упругое твёрдое тело во всех его точках возникают деформации, вызванные появлением в теле внутренних сил, сопротивляющихся внешним физическим воздействиям. Наиболее полно вопросы исследования напряженно-деформированного состояния в точке упругого твёрдого тела рассматриваются методами теории упругости.
Вкурсе сопротивления материалов показано, что внутренние силы в любой точке тела создают напряжения, являющиеся интенсивностью внутренних сил, отнесённых к единице площади. При этом полное напряжение разлагают на два взаимно перпендикулярных вектора – нормальное напряжение и касательное . У каждого вида напряжений имеются индексы. Так, у нормального напряжения имеется один индекс, указывающий на ось, параллельно которой направлен вектор нормального напряжения. У касательного напряжения имеются два индекса: первый показывает, что данное касательное напряжение действует на площадке с нормалью, параллельной одной оси (например, х), а второй обозначает, что вектор касательного напряжения параллелен другой оси (например, у).
Вслучае объёмного напряжённого состояния на гранях элементарного параллелепипеда со сторонами dx, dy, dz соответственно, выделенного в окрестности некоторой точки, будут действовать напряжения, показанные на рис. 1.
Рис. 1 |
5 |
Указанные на гранях элементарного параллелепипеда векторы напряжений принято считать положительными.
Приравнивая нулю сумму моментов всех касательных сил относительно осей x, y и z соответственно, можно получить следующие равенства:
xy yx ; |
yz zy ; |
zx |
xz. |
Полученные равенства описывают закон парности касательных напряжений при объёмном напряжённом состоянии.
В общем случае объёмного напряжённого состояния в любой точке упругого тела напряжённое состояние можно описать тензором Тн на-
пряжений[1, 4, 5, 6]:
|
|
x |
xy |
xz |
|
|
|
|||||
T |
|
|
|
|
|
|
|
|
|
. |
(1) |
|
|
yx |
y |
yz |
|||||||||
н |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zx |
zy |
z |
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
Элементы этого тензора называют компонентами тензора напряжений. Из девяти компонент тензора напряжений в силу закона парности касательных напряжений неизвестными являются шесть.
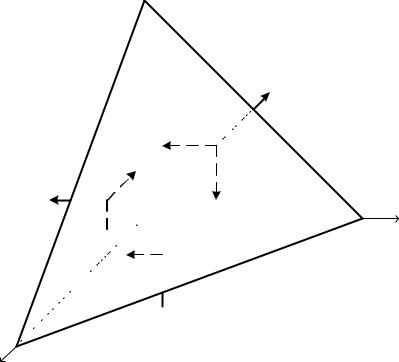
Если элементарный параллелепипед (см. рис. 1) мысленно рассечь наклонной плоскостью, то получится тетраэдр (рис. 2) бесконечно малых размеров, три взаимно перпендикулярные грани которого параллельны координатным плоскостям, а четвёртая – наклонная.
 y
y
y
|
|
xy |
x |
yx |
zy |
|
x
zx
 xz
xz 
 yz
yz
 z
z
z
Рис. 2
6
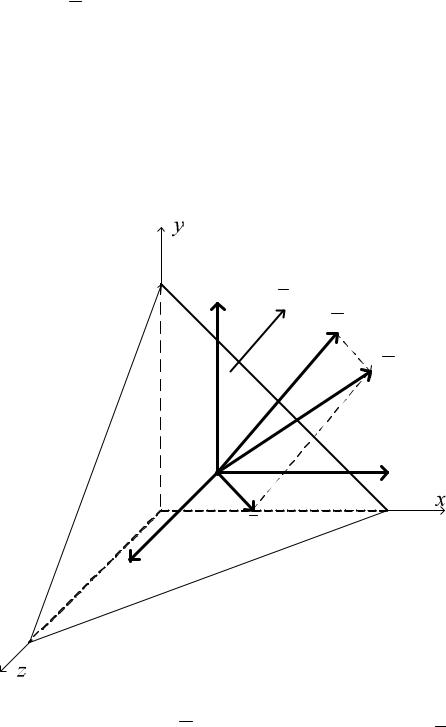
Положение наклонной площадки (рис. 3) описывается так называемыми направляющими косинусами: cos ,x , m cos , y , n cos ,z .
Если известны все компоненты напряжений, действующие на взаимно перпендикулярных площадках тетраэдра (для данной точки известен тензор напряжений Тн), единственным неизвестным будет вектор
полного напряжения P (см. рис. 3) на наклонной площадке. Рассматривая равновесие элементарного тетраэдра (см. рис. 2 и 3),
проецируя все силы на оси X 0, Y 0, Z 0, получим следующие выражения:
|
x |
xym xzn; |
|
|||||
Px |
|
|||||||
Py |
yx ym yzn; |
(2) |
||||||
P |
zx |
|
zy |
m |
z |
n. |
|
|
z |
|
|
|
|
|
|||
B |
|
P |
|
y |
|
|
|
|
P |
|
Px |
M |
|
|
C |
Pz |
|
A 
Рис. 3
Полный вектор напряжения P на площадке с нормалью , исходя из геометрии, будет определяться выражением
7

|
|
2 |
P |
2 |
P2 |
P2. |
(3) |
||
|
P |
||||||||
|
|
|
|
|
x |
y |
z |
|
|
Вектор полного напряжения |
|
|
|
|
можно разложить на две состав- |
||||
|
P |
|
|||||||
ляющие –перпендикулярную площадке (величина нормального напряжения Px Pym Pzn) и параллельную площадке (величина касатель-
ного напряжения |
|
|
|
2 |
|
2 |
|
|
|||||||
P |
|
). |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Из бесчисленного множества наклонных площадок, построенных в рассматриваемой точке упругого тела, можно выделить те, на которых отсутствуют касательные напряжения . Наклонные площадки, на которых касательные напряжения =0, называются главными площадками, а
действующие на них экстремальные нормальные напряжения называ-
ются главными напряжениями. Таких напряжений оказывается три. Исходя из определения главных площадок, можно записать сле-
дующие равенства: Px ; Py m; Pz n. С учётом системы уравнений (2) получается следующая система уравнений:
x xym xzn;
m yx ym yzn; (4)n zx zym zn.
После арифметического преобразования система (4) примет вид
x xym xzn 0; |
|
|||||
|
|
|
m |
|
n 0; |
(5) |
|
y |
yz |
||||
yx |
|
|
|
|
||
|
zym z n 0. |
|
||||
zx |
|
|||||
В системе уравнений (5) неизвестными являются направляющие косинусы ,m,n и главное напряжение . В качестве четвёртого уравнения используется известное из аналитической геометрии соотношение
2 m2 n2 1.
Известно, что система линейных однородных алгебраических уравнений имеет отличное от нуля решение в том случае, если определитель, составленный из коэффициентов при неизвестных, будет равен нулю. Следовательно, справедливой становится запись
x |
xy |
xz |
|
|
yx |
y |
yz |
0. |
(6) |
zx |
zy |
z |
|
|
8
После раскрытия определителя (6) получается кубическое уравнение относительно главных напряжений :
3 J 2 |
J |
J |
3 |
0. |
(7) |
1 |
2 |
|
|
|
В уравнении (7) коэффициенты J представляют собой инварианты напряжённого состояния, то есть их величины не меняются при повороте осей координат. Инварианты напряжений определяются формулами:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J1 x y z; |
|
|
|
|
|
|
|||||||
|
|
|
|
|
J |
2 |
|
y |
|
y |
|
z |
|
|
x |
2 |
|
2 |
2 |
; |
(8) |
||||||
|
|
|
|
|
|
|
|
x |
|
|
|
z |
|
xy |
yz |
|
zx |
|
|
||||||||
J |
|
|
x |
xy |
xz |
|
|
|
|
|
|
|
|
2 |
|
|
2 |
2 |
2 . |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
3 |
|
|
yx |
|
y |
|
|
yz |
|
|
|
z |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
x y |
|
xy |
|
yz zx |
|
x |
yz |
|
y zx |
z xy |
|||||||
|
|
|
zx |
zy |
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Корнями уравнения (7) являются главные напряжения, которые находятся в соотношении 1 2 3.
Контролем правильности определения главных напряжений служат равенства:
J1 1 2 3 ; J2 1 2 2 3 3 1; J3 1 2 3.
Для нахождения положения главных площадок, то есть значений направляющих косинусов cos ,x , m cos , y ; n cos ,z , следует подставить последовательно значения главных напряжений в систему уравнений (5). При этом вместо третьего уравнения используют соотношение 2 m2 n2 1. Так, например, для определения положения главной площадки, на которой действует главное напряжение 1, система уравнений имеет следующий вид:
|
|
1 |
xym1 xzn1 0; |
|
x 1 |
(9) |
|||
yx 1 y |
1 m1 xzn1 0; |
|||
2 |
m2 |
n2 1. |
|
|
1 |
1 |
|
1 |
|
Аналогичные системы уравнений можно записать для двух других главных напряжений.
Инженерная практика показывает, что прочность материалов зависит не только от величин компонентов напряжений, но и от характера напряжённого состояния. Так, большинство твёрдых тел противостоит без разрушения действию одинакового очень большого давления: и в то же время те же тела разрушаются при сравнительно невысоких напряжени-
9
