
1022
.pdf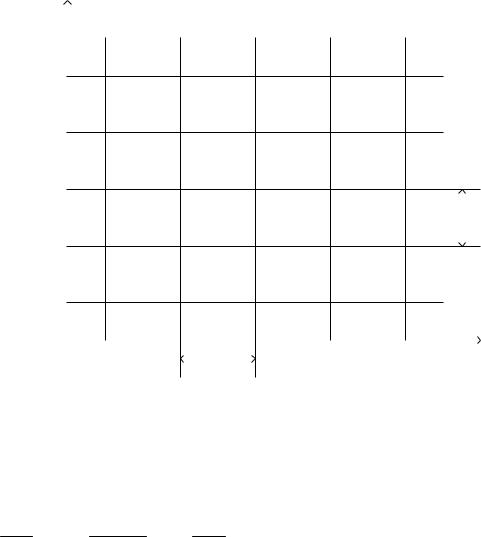
|
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
i 2 b d i |
n |
|
2 b d |
n |
|
||||||||||||
|
|
|
|
|
|
|
|
|
; |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
3 |
x |
x |
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
||||||||||||||
|
|
i |
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
2 x |
|
|
|
|
|
2 x |
|
|
|||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
2 |
|
2 |
|
|
4 b |
6 i 4 d |
n |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
x |
4 |
|
|
x |
2 |
x |
2 |
|
|
4 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
i |
|
|
|
|
i |
|
|
|
x |
|
|
|
|
|
|
|||||||||
|
|
|
a |
|
c |
|
||
Вдоль оси у: |
|
|
|
|
|
; |
||
|
|
|
|
|
||||
|
|
|
|
|
2 y |
|
|
|
|
y i |
|
|
|
|
|||
|
3 |
|
|
|
k 2 a c |
m |
|
|
|
|
|
; |
|||
|
y |
3 |
|
3 |
|
||
|
|
i |
|
2 y |
|
|
|
Смешанная производная
|
|
|
2 |
|
|
|
|
a 2 i c |
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|||||
|
|
y |
2 |
|
2 |
|
|
|
|||||
|
|
|
i |
|
y |
|
|
|
|
||||
|
4 |
|
|
|
|
k 4 a 6 i |
4 d |
n |
|
||||
|
|
|
|
. |
|||||||||
|
y |
4 |
|
|
|
4 |
|
|
|
||||
|
|
|
i |
|
|
y |
|
|
|
|
|||
|
4 |
|
|
|
|
|
4 i 2 a b c d e f g h |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
2 |
|
2 |
|
|
|
|
2 |
2 |
|
|
|
|
|
|||||
|
y |
|
|
|
|
|
|
|
|
|
||||||||
|
x |
|
|
|
i |
|
|
|
|
x |
y |
|
|
|
|
|
||
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
f |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
e |
a |
|
|
|
|
|
||||
|
|
|
|
|
|
|
n |
d |
i |
b |
l |
|
y |
|
||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
g |
|
|
|
|||
|
|
|
|
|
|
|
|
h |
c |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
x |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
Рис. 9 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда бигармоническое уравнение (42) после арифметических пре-
|
|
y 2 |
|
|
|
образований при обозначении |
|
|
|
|
для i-й точки примет |
|
|||||
|
|
|
|||
|
|
x |
|
|
|
вид x4 4 i 2 x24 y2 i y4 4 i 6 8 6 2 i 4 1 a c
30
|
|
4 1 b d 2 e f g h |
|
||||||||||||||||||||
|
|
|
2 n k m 0. |
|
|
|
…..(47) |
||||||||||||||||
В соответствии с изложенным можно записать формулы, с помо- |
|||||||||||||||||||||||
щью которых определяются значения напряжений: |
|
||||||||||||||||||||||
x |
|
2 |
|
a |
2 i |
c |
|
; y |
|
2 |
|
|
b 2 i d |
; |
(48) |
||||||||
|
|
|
|
|
|||||||||||||||||||
y2 |
|
|
2y |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
2x |
|
||||
|
|
|
|
|
2 |
|
|
|
|
f |
|
g |
|
h |
. |
(49) |
|||||||
|
|
xy |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
4 x y |
|
|
|
|
|
||||||||||||
|
|
|
|
|
x y |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Тринадцатичленное уравнение (47) может быть составлено для каждой внутриконтурной узловой точки сетки.При составлении уравнений для точек, лежащих вблизи контура в уравнения войдут значения для точек, принадлежащих как контуру, так и для близлежащих законтурных точек. Эти значения находятизграничныхусловийрассматриваемойконструкции.
Рассмотрим работу конструкции, называемую балкой-стенкой. Эта конструкция характерна тем, что размеры её высоты и длины сопоставимы между собой, а толщина несопоставимо мала по сравнению с этими размерами. Нагрузка действует только по торцам (контуру) балки-стенки. Задача расчёта балки-стенки в теории упругости относится к плоскому напряжённому состоянию.
При определении функций напряжений для точек, находящихся непосредственно на контуре и в ближайших законтурных точках, очень хорошо себя зарекомендовал метод, разработанный проф. П.М.Варваком – метод рамной аналогии [4]. В соответствии с этим методом значения функций Эри для точек, находящихся на контуре балки-стенки, определяются изгибающими моментами в раме, стороны которой совпадают с контуром бал- ки-стенки, а частная производная по перпендикулярному направлению определяется продольной силой в раме. Согласно этому значения функций Эри для точек, находящихся на контуре условной рамы, определяются формулой M . При этом, если изгибающие моменты отложены в эпюре с растянутой стороны стержня внутри контура рамы, то они считаются положительными. Значения функций Эри для точек, находящихся в ближайших законтурных точках, определяются поформулам:
для верхней и нижней граней законт внутр 2N y ; для левой и правой граней законт внутр 2N x.
Здесь N – ордината эпюры продольных сил в условной раме. Знак продольной силы N соответствует знаку на эпюре N.
После выражения значений функций напряжений в контурных точках и в ближайших законтурных точках через значения эпюры М в условной раме и эпюры N той же рамы для каждой внутренней точки по
31
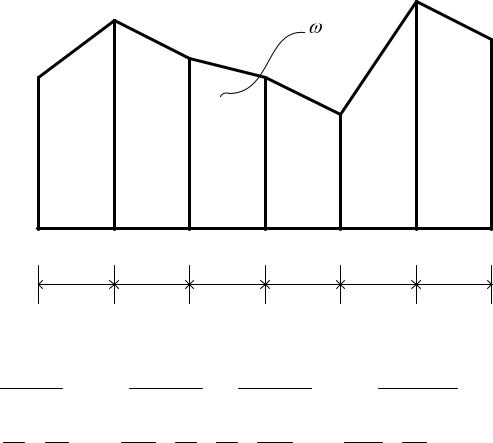
формуле (47) составляют тринадцатичленное алгебраическое уравнение, в котором неизвестными являются значения функций напряжений для внутриконтурных точек. Порядок полученной системы линейных алгебраических уравнений соответствует числу внутренних узлов сетки, нанесённой на контур рассматриваемой балки-стенки.
В результате решения полученной системы уравнений находят количественные значения функций напряжений в узлах сетки. Затем, формируя поле функций напряжений, по формулам (48) и (49) строят по сечениям соответствующие эпюры напряжений.
Проверкой правильности построения эпюр напряжений служит условие равновесия, представляющее собой сумму проекций на соответствующую ось всех сил, действующих на рассматриваемую часть балки-стенки.
Для проверки правильности построения, например, эпюры x
должно соблюдаться условие |
|
|
|
|
h |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X xdy F 0. |
|
|
(50) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
Вычислить интеграл (46) можно численно, используя, например, |
|||||||||||||||||||||
формулу трапеции. Согласно этой формуле интеграл определяется как |
|||||||||||||||||||||
обычная площадь трапеции. |
|
|
|
Эпюра |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
|
|
i 1 |
|
|
|
i |
|
|
i 1 |
|
|
|
n |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 |
|
|
|
|
i 1 |
|
|
|
i |
|
i 1 |
|
|
|
|
n |
||
|
|
|
|
|
|
d |
d |
|
|
|
d |
|
|
d |
|
|
d |
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 10 |
|
|
|
|
|
|
|
||
Прирегулярномшагевеличинаплощадиэпюрысводитсяквыражению |
|||||||||||||||||||||
1 |
2 |
d ... i 1 i |
d i |
i 1 |
d ... n 1 |
n |
d |
||||||||||||||
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
2 |
|
(51) |
|
|
|
1 |
|
|
2 |
|
i 1 |
|
i |
|
i |
|
i 1 ... |
|
n 1 |
|
n |
|
|||
|
|
||||||||||||||||||||
d |
|
|
... |
|
|
|
|
|
. |
|
|||||||||||
|
2 |
|
2 |
|
2 |
2 |
|
2 |
|
2 |
|
|
2 |
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
|
|
|
|
|
|
||
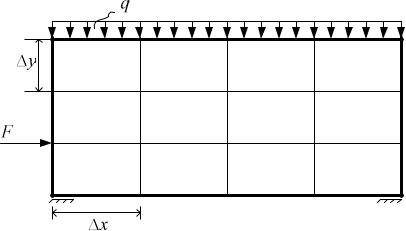
После приведения подобных слагаемых в скобке получим формулу для определения площади эпюры напряжений:
|
|
1 |
|
i n 1 |
|
n |
|
|
d |
|
|
i |
|
. |
(52) |
||
|
|
|
|
|||||
2 |
i 2 |
2 |
|
|||||
Контрольные вопросы
1.Дать определение и привести пример плоской деформации.
2.Дать определение и привести пример обобщённого плоского напряжённого состояния.
3.Назвать методы решения плоской задачи теории упругости.
4.Перечислить группы уравнений теории упругости.
5.Написать и пояснить физическую суть уравнений Навье.
6.Написать и пояснить физическую суть соотношений Коши.
7.Написать и пояснить физическую суть уравнений закона Гука в прямой форме.
8.Написать и пояснить физическую суть уравнения Мориса−Леви.
9.Что такое функция напряжений и каким условиям она должна удовлетворять.
10.Написать и пояснить физическую суть бигармонического уравнения.
11.Пояснить идею метода конечных разностей при решении плоской задачи теории упругости.
12.Пояснить суть рамной аналогии при определении значений функций напряжений на контуре балки-стенки и в её ближайших законтурных точках.
13.Написать формулы для определения напряжений в методе конечных разностей.
14.Написать и пояснить формулы для контроля правильности построения эпюр напряжений в балке-стенке.
4. ПРИМЕР РАСЧЁТА БАЛКИ-СТЕНКИ
Исходные данные: 19м, h 18м, F 50кH, q 9 кH/м. Заданная схема балки-стенки показана на рис. 11.
Рис. 11
33
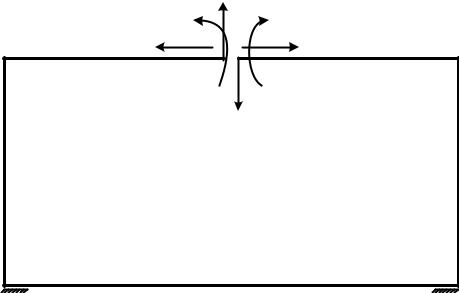
1. Выбор из заданной системы условной рамы основной системы и построение в ней грузовой эпюры моментов.
Условная рама является по методу сил трижды статически неопределимой системой. Поэтому при выборе основной системы необходимо устранить три «лишних» связи. Разрезая жёсткое сечение верхнего горизонтального элемента рамы (ригель), тем самым устраняются три «лишних» связи.
X1 |
X3 |
X3 |
|
X2 |
X2 |
X1 |
|
Рис. 12 |
|
На рис.12 показана принятая для решения данной задачи условная основная система метода сил.
2. Формирование поля функций напряжений.
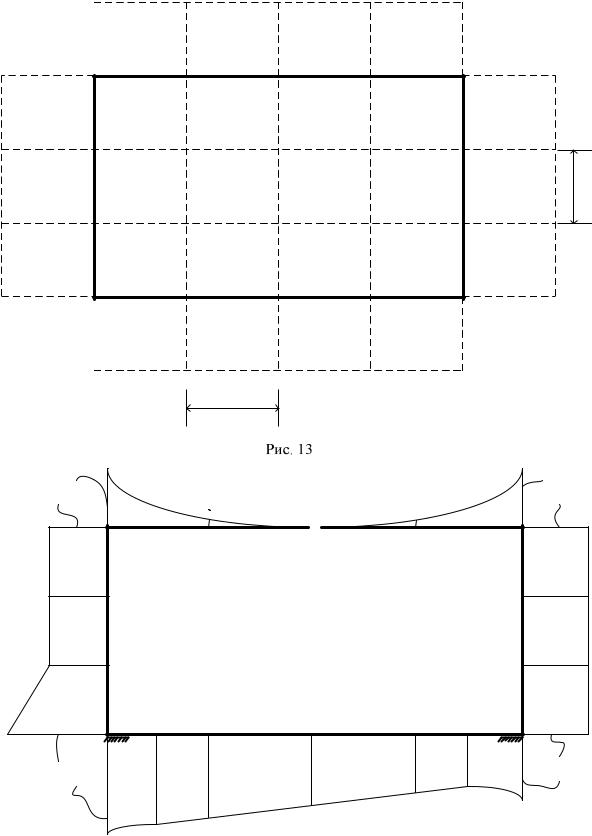
На рис. 13 показано исходное поле функций напряжений для данной задачи. В соответствии с рамной аналогией для выражения функций напряжений, находящихся в точках на контуре условной рамы и в бли-
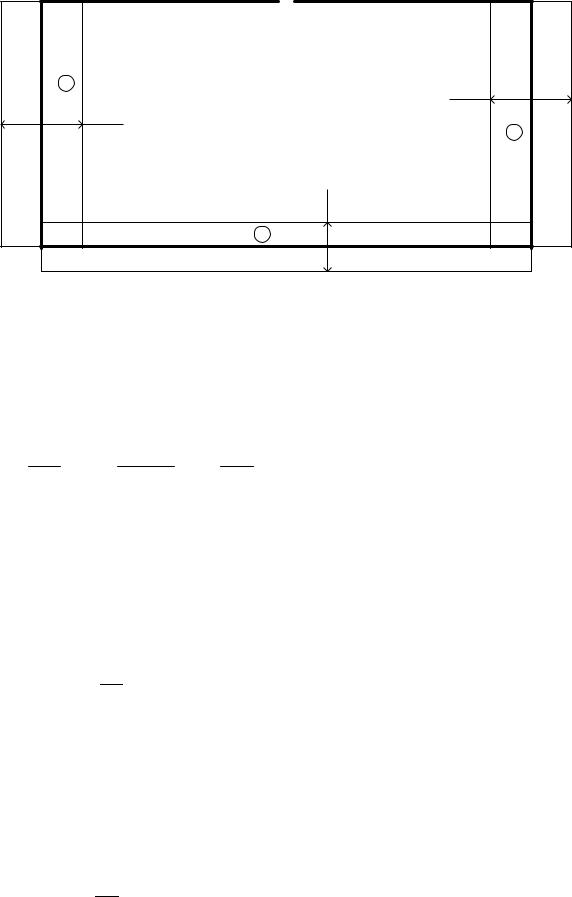
жайших законтурных точках, построены эпюры моментов − эпюра MF0 (рис. 14) и эпюра N (рис. 15).
Для определения этих значений использованы следующие соотношения: конт M ;
для верхней и нижней граней законт внутр 2N y ; для левой и правой граней законт внутр 2N x.
Согласно приведённым соотношениям были найдены значения функций напряжений, находящихся в точках на контуре условной рамы и в ближайших законтурных точках (рис. 14).
34
|
законт |
законт |
|
законт |
законт |
законт |
|
||
законт |
конт |
конт |
|
конт |
|
конт |
конт |
законт |
|
законт |
конт |
1 |
|
2 |
|
3 |
|
конт |
законт |
законт |
конт |
6 |
|
5 |
|
4 |
|
конт |
y |
|
|
|
законт |
||||||
законт |
конт |
конт |
конт |
конт |
|
|
конт |
законт |
|
|
законт |
законт |
|
законт |
законт |
|
законт |
|
|
|
|
x |
|
|
|
|
|
|
|
406,125 |
|
|
|
|
|
|
|
406,125 |
|
|
|
101,531 |
|
|
|
101,531 |
|
||
|
406,125 |
|
Эп.МF0 |
|
|
406,125 |
|||
|
|
|
|
|
|
|
|
||
|
406,125 |
|
|
|
|
|
406,125 |
||
|
|
567,0938 |
454,5938 |
342,0938 |
|
||||
706,125 |
|
|
|
|
|
|
|
406,125 |
|
|
|
|
|
Рис. 14 |
|
|
|
|
|
|
|
|
|
35 |
|
|
|
|
|
|
|
85,5 |
85,5 |
|
|
Эп.NF0 |
|
|
|
50,0 |
|
|
|
|
|
Рис. 15 |
|
3.Определение значений функций напряжений для внутриконтурных точек.
Используя тринадцатичленное уравнение
x4 4 i 2 x24 y2 i y4 4 i 6 8 6 2 i 4 1 a c
4 1 b d 2 e f g h 2 n k m 0,
сформируем для внутренних точек соответствующие выражения. Cначала найдём постоянные коэффициенты этого уравнения:
1,5956; 2 2,5459; 2 3,1912; 4 1 10,3824.
6 2 8 6 6 1,59562 8 1,5956 6 34,0404, 4 1 16,5578.
Для узла 1:
34,0404 1 10,3824 101,5313 6 16,5578 406,125 2
3,1912 406,125 0 5 406,125 2,5459 3 1 812,25
1 567,0938 0.
После преобразований получим
37,5863 1 16,5662 2 2,5459 3 0 4 3,1912 510,3824 6 2555,0160 0.
Для узла 2:
36

34,0404 2 10,3824 0 5 16,5578 3 1
3,1912 101,5313 101,5313 4 6 2,5459 406,125 406,125
2 454,5938 0.
После преобразований получим
16,5662 1 35,0404 2 16,5662 3 3,1912 4 10,3824 5
3,1912 6 3170,5144 0.
Для узла 3:
34,0404 3 10,3824 101,5313 4 16,5578 406,125 2
3,1912 0 406,125 406,125 6 2,5459 3 812,25 1
3 342,0938 0.
После преобразований получим
2,5459 1 16,5662 2 37,5863 3 10,3824 5
0 6 2780,0160 0.
Для узла 4:
34,0404 4 10,3824 3 342,0938 16,5578 5 406,125
3,1912 2 406,125 406,125 454,5938 2,5459 6 4 812,25
101,5313 4 600 0.
После преобразований получим
0 1 3,1912 2 10,3284 3 37,5863 4 16,5662 52,5459 6 3467,4949 0.
Для узла 5:
34,0404 5 10,3824 2 454,5938 16,5578 6 4
3,1912 1 3 342,0938 567,0938 2,5459 406,125 406,125
0 5 600 0.
После преобразований получим
3,1912 1 10,3824 2 3,1912 3 16,5662 4 35,0404 5
16,5662 6 849,5321 0.
Для узла 6:
34,0404 6 10,3824 1 567,0938 16,5578 406,125 5
3,1912 406,125 2 454,,5938 706,125 2,5459 6 812,25
4 6 600 101,5313 0.
37
После преобразований получим
10,3824 1 3,1912 2 0 3 2,5459 4 16,5662 537,5863 6 4846,1749 0.
Решая полученную систему линейных алгебраических уравнений шестого порядка, были найдены значения функций напряжений для внутренних узловых точек рассматриваемой балки-стенки:
1 117,7352; |
2 |
25,6022; |
3 |
111,9944; |
4 169,3219; |
5 |
141,9274; |
6 |
210,3683. |
Получившееся поле функций напряжений показано на рис. 16.
|
406,125 |
1 |
2 |
3 |
406,125 |
|
|
||
|
406,125 |
101,5313 |
0 |
101,5313 |
406,125 |
|
|
||
|
|
|
|
|
3 |
|
|
|
|
|
406,125 |
2 |
406,125 |
|
|
||||
|
1 |
|
|
|
|
||||
1 |
812,25 |
|
|
|
|
|
3 |
812,25 |
|
|
|
|
|
|
|||||
|
406,125 |
6 |
5 |
4 |
406,125 |
|
|
||
6 |
812,25 |
|
|
|
|
|
4 |
812,25 |
|
y
706,125 |
567,0838 |
454,5938 |
342,0938 |
406,125 |
|
6 600 |
5 600 |
4 600 |
|
x
Рис. 16
4. Определение ординат и построение эпюр напряжений.
38
Для определения ординат эпюр напряжений используем соотношения, выраженные в конечных разностях, принятые при решении уравне-
ния М. Леви: |
x |
|
2 |
|
a 2 i c |
; |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
y2 |
|
|
|
2y |
|
|
|
|
|
|
|
|||
y |
|
2 |
|
|
b |
2 |
i |
|
d |
; xy |
|
|
2 |
f g |
h |
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x2 |
|
|
|
2x |
|
|
|
4 x y |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x y |
|
|
|||||||
На рис. 17 показаны положения сечений I-I, II-II, III-III, A-A и B-B, в которых построены эпюры напряжений.
Сечение I-I. |
Ординаты эпюры x: |
|
|
точка 1 |
|
|
|
x 1 |
117,7352 2 101,5317 117,7352 |
0,9002кH/м2; |
|
|
|||
точка 2 |
62 |
|
|
|
|
||
x 2 |
|
|
101,5313 2 117,7352 210,3683 |
|
|
2,1230 кH/м2; |
|
|
|
||||||
|
62 |
|
|
|
|||
точка 3 |
|
||||||
x 3 |
|
117,7352 2 210,3683 567,0938 |
|
7,3359 кH/м2; |
|||
|
|
||||||
|
62 |
|
|
|
|||
точка 4 |
|
||||||
x 4 |
|
210,3683 2 567,0938 810,3683 |
3,1514 кH/м2. |
||||
|
|||||||
|
62 |
|
|
|
|||
Сечение II-II. Ординаты эпюры x:
точка 5
x 5 |
|
|
25,6022 2 0 25,6022 |
1,4223кН/м2; |
|||
|
|
|
|||||
|
62 |
|
|
|
|||
точка 6 |
|
|
|
||||
x 6 |
|
|
0 2 25,6022 141,9274 |
2,5201кH/м2; |
|||
|
|
||||||
|
62 |
|
|
|
|||
точка 7 |
|
|
|
||||
x 7 |
|
25,6022 2 141,9274 454,5938 |
5,4539кH/м2; |
||||
|
|||||||
|
62 |
|
|
|
|||
39
