Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1022

.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

821.62 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

7. Определение интенсивности напряжений.

Интенсивность напряжений определяется по формуле

				i	1	1 2 2		2 3 2 3 1 2 .


				2
		В настоящей задаче интенсивность напряжений будет равна
i		1		74,87 20,74 2 20,74 34,13 2 34,13 74,87 2
				74,87 20,74 2 20,74 34,13 2 34,13 74,87 2
		2
		2		1
				1			104 МПа.
			95,612 13,392 1092
	2		95,612 13,392 1092

8. Определение тензора деформаций в рассматриваемой точке упругого тела.

Определим компоненты тензора деформаций (16). Для этого используем закон Гука в прямой форме (21). Прежде чем определять деформации, приведём эти формулы к единому модулю деформации Е, воспользовавшись известной из курса сопротивления материалов зави-

симостью G 21 , в соответствии с которой найдём

0,38E.

21 0,32

Исходя из этого, найдём:

10 0,32 20 30

6,8

;

20 0,32 30 10

32,8

;

30 0,3210 20

33,2

;

52,63

;

105,26

; zx

78,94

0,38E

По полученным данным тензор деформации примет вид

					1		1
			6,8			52,63		105,26
			6,8		2	52,63	2	105,26			6,8	26,31	52,63
					2		2				6,8	26,31	52,63
Тд	1	1					1			1
				52,63	32,8				78,94		26,31	32,8	39,48 .
				52,63	32,8				78,94		26,31	32,8	39,48 .
	Е	2			1		2			E	52,63	39,47	33,2
		1	105,26		1	78,94			33,2
		2	105,26		2	78,94			33,2
		2			2

9. Определение инвариантов деформированного состояния в точке упругого тела.

						D						x			y					z		1		6,8 32,8 33,2																			6,4				;
						D																2		6,8 32,8 33,2																							;
								1														2																						E
										D																								1		2		2						2
										D																												2
												2			x			y			y		z					z		x			4			xy			yz					zx
							1																																							1		2
									6,8 32,8 32,8 33,2 33,2 6,8																																							26,31
						E		2	6,8 32,8 32,8 33,2 33,2 6,8																																					4		26,31
						E		2							1											1												2346,47								4
															1						2					1							2					2346,47
																	52,63										39,47															.
															4		52,63									4	39,47												E2			.
															4											4													E2
D														1											1						2						2				2
D																																									2
	3		1				x		y		z		4			xy			yz		zx		1			4			x		yz				y		xz			z	xy
			1		6,8 32,8 33,2																		1			26,31 39,47 52,63
		E3			6,8 32,8 33,2																					26,31 39,47 52,63
		E3																					4
	1																																												195157,29
				6,8 39,472														32,8 52,632														33,2 26,312																	.
	4			6,8 39,472														32,8 52,632														33,2 26,312																E3	.
	4																																															E3

10. Определение шарового тензора деформаций и девиатора деформаций.

Прежде чем находить компоненты этих тензоров, найдём величину

		x y z		0	1 2	6,671 2 0,32	2,4	.
0
			E
	3					3E	E

В соответствие с этим шаровой тензор деформаций и девиатор деформаций примут вид

		0		0		0		1	2,4		0	0
Т	0		0			0				0	2,4	0	шаровой тензор деформаций;
	д				0
								E
			0							0	0
				0			0					2,4

											xy			xz
					x			0			xy			xz

											2			2
						yx					2			2
D	д					yx			y			0	yz
D							2							2
							2							2
							zx			zy		z
							zx								0
							2				2				0
							2				2
											52,63				105,26
			6,8 2,4
	1		6,8 2,4									2			2		9,2		26,31	52,63
	1				52,63										78,94	1
									32,8 2,4									26,31	35,2	39,47
									32,8 2,4									26,31	35,2	39,47
		E					2								2	E			39,47
		E					2				78,94				2	E	52,63		39,47	30.08
				105,26							78,94
															33,2 2,4
							2					2			33,2 2,4
							2					2

девиатор деформаций.

11. Определение интенсивности деформаций.

Интенсивность деформаций через компоненты тензора деформаций может быть определена по формуле

	2				3
i		x	y 2 y	z 2 z x 2		xy2	yz2	zx2 .
i	3	x	y 2 y	z 2 z x 2	2	xy2	yz2	zx2 .
	3				2

Для данной задачи интенсивность деформаций будет равна

		0,47			6,8 32,8 2 32,8 33,2 2					33,2 6,8 2
i
i			E		2	105,26	2	78,94	2
			E		1,552,63	105,26		78,94
	56,94			28,47 10 5.
		E		28,47 10 5.
		E

Далее приводятся состав задания и исходные данные для выполнения расчётно-графической работы «Исследование напряжённодеформированного состояния в точке упругого тела».

Состав задания

При известных модуле упругости Е = 2 105 МПа и коэффициенте Пуссона = 0,32 требуется:

1.Показать напряжения на координатных площадках. Определить тензор напряжений.

2.Найти напряжения на наклонной площадке.

3.Найти инварианты тензора напряжений в рассматриваемой точке.

4.Определить величины главных напряжений.

5.Найти направления главных напряжений.

6.Определить шаровой тензор напряжений и девиатор напряжений.

7.Определить интенсивность напряжений.

8.Определить тензор деформаций в рассматриваемой точке упругого тела.

9.Найти инварианты деформированного состояния в рассматриваемой точке упругого тела.

10.Найти шаровой тензор деформаций и девиатор деформаций.

11.Найти интенсивность деформаций.

				Исходные данные										Таблица 1

		Напряжения, МПа								Направляющие
											косинусы
№
п/п	х	у	z	ху	yz	zx		l			m					n

1	-100	-100	-100	-50	80	100	0							/2	1/2
												3
2	180	180	-60	-60	120	-60	1/2				0						/2
																3
3	140	60	100	100	50	40	0				1/2							/2
																3
4	-100	-80	-120	80	90	90	0						/2		1/2
												3
5	110	130	60	-50	100	90	1/2				3/2				0
6	-120	-60	-120	100	60	60				/2	1/2				0
								3
7	-120	-80	-100	60	100	90	0						/2		1/2
												3
8	110	90	100	90	90	60	0							/2	1/2
												3
9	150	70	80	-90	-80	60	1/2				0						/2
																3
10	-140	-60	-100	60	100	90			/2		0				1/2
								3
11	150	90	60	100	-50	50	1/2				0						/2
																3
12	130	100	70	90	100	90	0						/2		1/2
												3
13	-70	-130	-100	120	60	90	0				1/2						/2
																3
14	80	100	120	-60	-80	-70			/2		0				1/2
								3
15	60	80	100	-70	-90	100	1/2				3/2				0
16	-100	80	120	80	-70	90				/2	0				1/2
								3
17	80	-70	-100	120	100	60	1/2				0						/2
																3
18	-60	-100	80	70	-120	100	3/2				0				1/2
19	60	-80	-100	70	120	80	1/2							/2	0
												3
20	-60	70	80	-100	120	-120	0							/2	1/2
												3
21	-40	60	-70	35	100	-60			/2		1/2				1/2
								3
22	90	-120	50	40	-85	70	1/2				0						/2
																3

3. ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ. БАЛКА-СТЕНКА

Втеории упругости различают два вида плоских задач [1, 3, 4, 5, 6]:

задача о плоской деформации и плоское напряжённое состояние.

Плоской деформацией называется деформация, при которой перемещения всех точек тела параллельны одной плоскости. Характерным примером плоской деформации может служить бесконечно длинная подпорная стенка, имеющая по всей длине одинаковое поперечное сечение,

ипри этом на стенку по всей её длине действует одинаковая внешняя нагрузка.

Плоским напряжённым состоянием называется такое состояние тела, при котором напряжения по всем элементарным площадкам, параллельным какой-либо плоскости, равны нулю, а напряжённое состояние во всех точках, лежащих на одном перпендикуляре к этой плоскости, одинаково. Характерным примером плоского напряжённого состояния является работа пластины, испытывающая нагружение только по её торцам, а поверхность пластины свободна от нагружения.

Втеории упругости имеется три основных метода решения плоской задачи – в перемещениях, в напряжениях и смешанный метод.

Прежде чем рассматривать любой из этих методов, представим три группы уравнений теории упругости – статические, геометрические и физические [2,4,6].

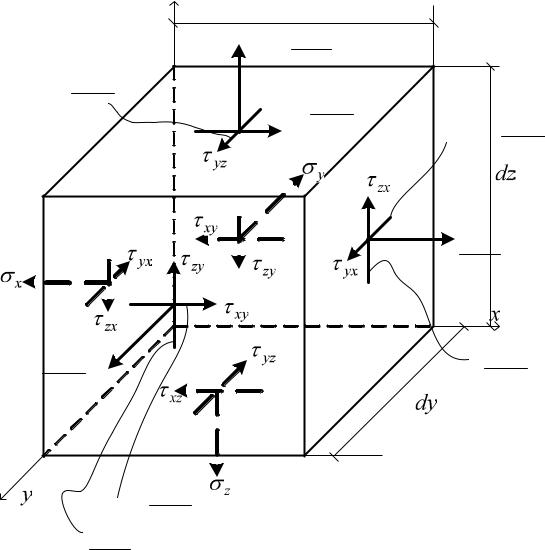
Статические уравнения описывают взаимосвязь между силами и напряжениями. Из рассмотрения равновесия элементарного параллелепипеда (рис. 7) при составлении уравнений, представляющих собой суммы проекций сил, действующих на гранях этого параллелепипеда на соответствующие оси координат, были получены дифференциальные зависимости (30), называемые уравнениями Навье.

(30)

			z
			z	z	dz
		xz xz dz		z
		xz xz dz			yz	dz
		z	yz		yz	dz		yx	dx
				z			yx	yx	dx
							x
						x	x dx
							x
		y dy				zx zx dx
	y	y					x
		xy	xy dy
		zy zy	y
		zy zy	dy
		y
			Рис. 7
Геометрические уравнения (31) устанавливают связь между пере-
мещениями и деформациями и называются уравнениями Коши:

;

(31)

;

К геометрическим уравнениям относятся и уравнения, равенства которых доказывает отсутствие в упругом теле, подверженному деформированию, разрывов, трещин или отверстий. Эти уравнения (32) называются уравнениями неразрывности Сен-Венана:

2 x 2 y 2 xy ;y2 x2 x y

2 y 2 z 2 yz ;z2 y2 y z

2 z 2 x 2 zx ;x2 z2 x z

;

(32)

y z

2 y

;

z x

y x

Физические уравнения описывают зависимость между деформациями

и напряжениями, что соответствует закону Гука в прямой форме (21).

Рассмотрим решение задачи плоского напряжённого состояния в на-

пряжениях

[1,4].

качестве

неизвестных напряжений

являются:

х х, у ; у

у х, у ;

ху ух х, у . Задача состоит в том, что для

плоского напряжённого состояния из девяти уравнений (уравнения равновесия Навье (30), геометрические соотношения Коши(31), уравнения неразрывности деформаций (32) и физические соотношения закона Гука в прямой форме (21)) необходимо получить три уравнения. Для этой цели возьмём два уравнения Навье и одно уравнение неразрывности деформаций.

Уравнения равновесия Навье


		х		ху		0;


х			у		.
	ух
					у	0.

	х		у

Уравнение совместности деформаций

2 х 2 у 2 ху .у2 х2 х у

(33)

(34)

Соответствующие производные из физических соотношений закона Гука (35) подставим в уравнение (34) совместности деформаций.

				1	х у ;
	х
	х			Е
				Е
				1	у x ;		(35)
	у
	у			Е
				Е	xy 21
		ху			xy 21		.
ху

			G			E
			G			E

После преобразований получим

2 х

2 у

2 х

2 ху

(36)

у2

х2

х у

у2

х2

Для исключения из уравнения (36)

касательного напряжения ху

воспользуемся уравнениями (33). Для этого продифференцируем первое уравнение по координате х, а второе – по координате у и просуммируем два полученных уравнения:

2 х

2 ху

х2

у х

2 ух

2 у

х у

у2

__________________

2 х

2 у

2 ху

(37)

х2

у2

х у

Подставим уравнение (37) в уравнение (36):

2 х

2 у

2 х

2 у

(38)

После преобразований уравнение (38) принимает вид

2 x

2 y

(39)

Первые два слагаемых в выражении (39) представляют собой диф-

ференциальный оператор Лапласа

2 x

, а вторые соот-

ветственно 2 y 2 y 2 y . Выражение (39) можно преобразовать

x2 y2

следующим образом: 2 x 2 y 0 2 x y 0.

Сумма напряжений в скобках представляет собой первый инвариант напряженийJ1 x y для плоского напряжённого состояния. В

итоге можно записать
2J1 0.	(40)

Выражение (40) – уравнение Мориса−Леви.

Задача определения напряжений из уравнения Мориса−Леви значительно упрощается, если в уравнение (40) ввести некую функциюx, y функция Эри, которая должна обязательно удовлетворять

следующим условиям: x	2			2	;		2
		;	y			xy		.
	y2			x2			x y

Подставим первые два условия в уравнение Мориса−Леви:

	2		2
2					0 2 2 0 4 0.	(41)
		2		2
	y		x

В развёрнутом виде уравнение (41) имеет вид

4	2	4	4	0.	(42)
x4		x2 y2	y4

Уравнение (42) есть бигармоническое уравнение.

Вматематике имеется несколько численных способов решения таких дифференциальных уравнений.

Для широкого класса задач теории упругости удобным численным методом интегрирования бигармонического уравнения явился метод конечных разностей (метод сеток) [2,4,7]. Идея метода конечных разностей состоит в том, чтобы решение плоской задачи через функцию напряжений Эри, определяемую бигармоническим уравнением (42), свести к системе линейных алгебраических уравнений.

Вэтом методе частные производные бигармонического уравнения приближённо заменяются конечными разностями, в результате чего оно превращается в алгебраическое.

Напомним основные положения метода конечных разностей. Рассмотрим некоторую непрерывную функцию x (см. рис.8) и допустим,

что известны значения этой функции для некоторых значений х, а именно: x лев. при x x; x 0 при х 0 и x прав. при

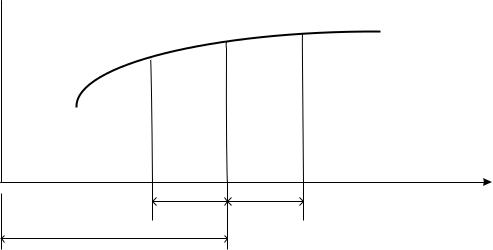
х х. Предположим, что функция x представлена уравнением па-


раболы: x ax2		bx c.	x 0		(43)
	Коэффициенты а, b и с найдём из условий: при х 0		x 0		c;
при	x x	x a x 2 b x c лев.; При		x x

x a x 2 b x c прав .

Решая совместно два последних уравнения, найдём

лев 2 0

прав

лев

; b

2 2x

2 х

Подставляя в (39) найденные выражения для a, b и c, запишем:

лев 2 0

прав

прав лев

x 0 .

(44)

2 2x

2 x

Дважды продифференцируем выражение (44) по координате х:

лев

2 0 прав

прав. лев

;

(45)

2 2x

2 x

лев

2 0 прав

(46)

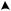
		прав.
	лев.	0

i-1	0	i+1	x
x		x

Рис. 8

На основании формул (45) и (46) составим выражения производных в конечных разностях для сетки (рис. 9) с прямоугольными ячейками, размер которых равен xи y .

b 2 i

Вдоль оси х:

;

2 x

x i

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.2021820.52 Кб71018.pdf
#
07.01.2021820.79 Кб71019.pdf
#
07.01.2021289.08 Кб3102.pdf
#
07.01.2021821.59 Кб41020.pdf
#
07.01.2021821.59 Кб11021.pdf
#
07.01.2021821.62 Кб51022.pdf
#
07.01.2021821.88 Кб61023.pdf
#
07.01.2021821.9 Кб31024.pdf
#
07.01.2021822.13 Кб31025.pdf
#
07.01.2021823.73 Кб111026.pdf
#
07.01.2021824.03 Кб61027.pdf