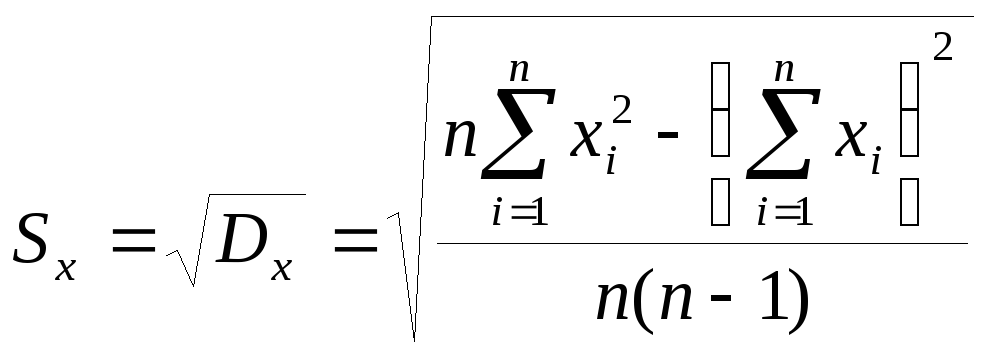- •Разработка и исследование нестандартного программного генератора случайных величин для имитационной модели Введение
- •1.Цель работы
- •2.Содержание
- •3.Теоретическая (расчетная) часть
- •1.Метод обратного преобразования (моп).
- •2.Универсальный метод н.П.Бусленко.
- •Проверка качества генератора
- •4.Программная реализация
- •Варианты
- •Отчетность
Варианты
выполнения лабораторной работы с расчетными формулами для различных типов функции распределения случайных величин и методов моделирования (сводная таблица).
|
Тип графика функции распределения |
Вар.1 МОП |
Вар.2 УМ |
Ti |
|
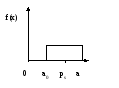
0 а
f(x) |
|
j = [1 + q*]
|
|
|
| |||
|
0 a |
Вар.3
|
Вар.4
j =[1 + q*]
|
|
|
| |||
|
|
Вар.5
|
Вар.6
j = [1 +q*]
|
|
|
|
|
|
|
| ||||
|
|
|
| ||||||
|
Тип графика функции распределения |
Вар.7 МОП |
Вар.8 УМ |
Ti | |||||
|
|
j = [1 +q*]
|
| ||||||
|
| ||||||||
|
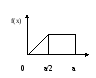
f(x)
0 a/2 a |
Вар.9 МОП
|
Вар.10 УМ
j = [1 +q*]
|
| |||||
|
| ||||||||
|
|
Вар.11 МОП
|
Вар.12
|
|
|
| |||
|
|
Вар.13 МОП
|
| |
|
f(x) |
Вар.14 УМ
j = [1 +q*]
|
| |
|
| |||
|
Тип графика функции распределения |
Вар.15 УМ |
Тi | ||||||
|
|
Накл.уч.
Гориз.
уч.
|
| ||||||
|
| ||||||||
|
|
Вар.16 УМ
q = 12,18,24…
j
= [1 +q*]
|
| ||||||
|
| ||||||||
|
|
|
|
|
| ||||
|
|
|
| ||||||
|
| ||||||||
|
|
|
| ||||||
|
|
|
| ||||||
|
|
|
|
|
|
|
Вар.17 УМ
j = [1 +q*]
|
|
|
| ||
|
|
Вар.18 МОП
|
|
|
|
Вар.19, 20, 21 ЦПТ
=
F(x) = Ф0(x) табл. интеграл |
|
Отчетность
На защиту лабораторной работы студент должен предоставить:
1) Работающую программу генератора в среде Excelпо своему варианту задания, выполненную в соответствии с примером, рассмотренным в данных Методических указаниях.
2) Промежуточные выкладки расчетных формул для характеристик распределения и разыгрывания СВ по своему варианту с пояснениями в виде краткого отчета.
Кроме того, студент должен продемонстрировать умение ориентироваться в статистических методах оценки и использовать среду Excelдля получения критических значений используемых распределений СВ и автоматизации формирования заключения о качестве генератора.






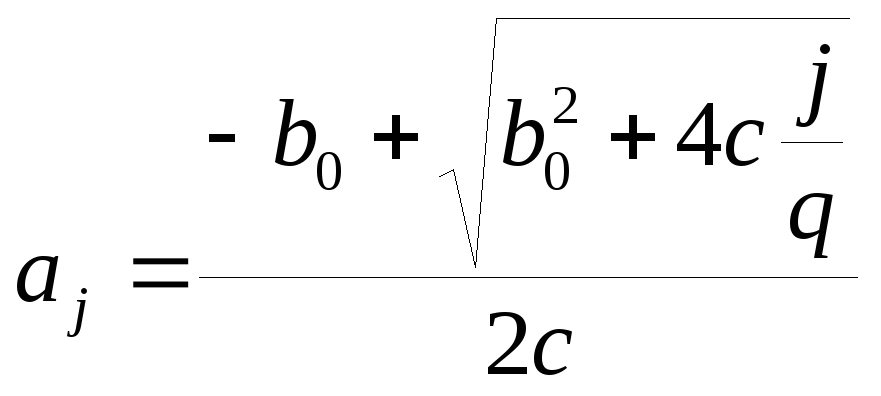
 ;
F(x)=cx2
+ b0x
;
F(x)=cx2
+ b0x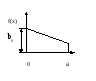

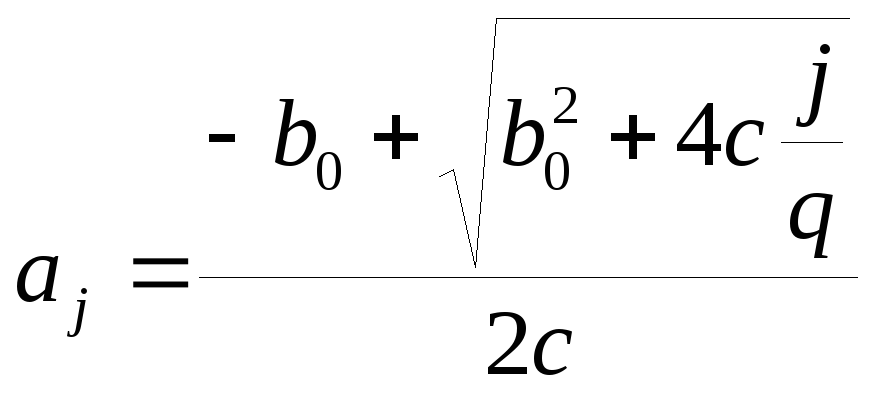
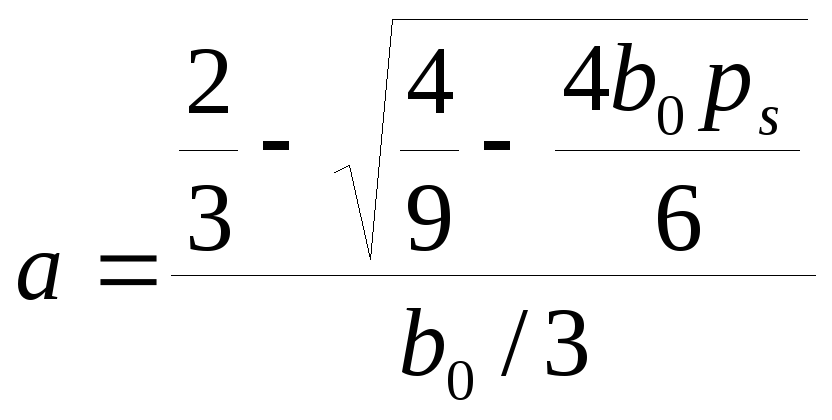











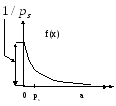
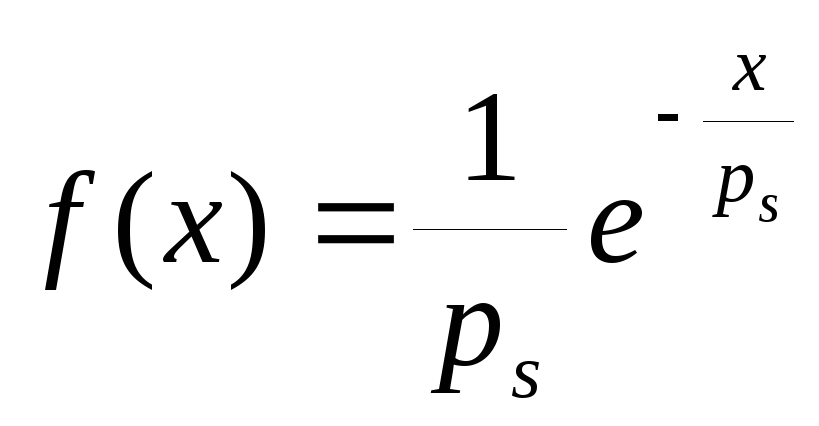 M(x)=1/(1/ps)=ps
M(x)=1/(1/ps)=ps