Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

447

.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

505.28 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

dS	Q
dS	T .	(4.5)

Здесь dS = const, а изменяется только правая часть уравнения, т.е. значение величины теплоты. Единицы измерения энтропии: [S] = Дж/моль·К.

Объединенное уравнение первого и второго закона термодинамики:

				(4.6)
TdS dU pdV A.
Расчет изменения энтропии идеального газа.
Выразим изменение внутренней энергии			dU CvdT.
Разделив уравнение (4.6) на Т , определим изменение энтропии:
dS	CvdT	p	dV.	(4.7)
		T
	T
Из уравнения идеального газа: pV RT			следует, что	p	R	.

				T V

Тогда, после подстановки этого соотношения в (4.7):

CvdT

(4.8)

Проинтегрируем

выражение (4.8)

при Cv

const и

получим

уравнение для расчета изменения энтропии идеального газа:

ΔS Cv

Rln

(4.9)

Изотермический процесс, T const:

ΔS Rln

(4.10)

так как

, то

ΔS Rln

(4.11)

Изохорический процесс, V const:

ΔS Cv Rln

(4.12)

Изобарический процесс, p const:

ΔS Cp Rln	T2
		.	(4.13)
	T	.	(4.13)
Адиабатический процесс, Q 0:	1
Адиабатический процесс, Q 0:
ΔS 0.			(4.14)

Постулат Планка имеет следующую формулировку: при абсолютном нуле энтропия правильно образованных кристаллов чистых веществ равна нулю. Постулат позволяет рассчитать абсолютное значение энтропии, если известны теплоты фазовых переходов, и если известны теплоёмкости вещества в различных агрегатных состояниях.

Рассмотрим вычисление изменения энтропии в различных процессах.

1. Изменение энтропии S при фазовых переходах (T = const)

определяется по формуле

S n H	(4.15)
T ,

где ∆H - теплота фазового перехода (кипение, испарение, возгонка, плавление); n – число моль вещества, переходящего из одной фазы в другую; n = g/M, где g – масса вещества, M – его молярная масса.

2. Изменение энтропии ∆S при нагревании. а) Пусть p = const, тогда Q CpdT ,


dS	CpdT
dS	T .				(4.16)
	T .				(4.16)
Если Cр = const, тогда			T2
∆S = Cр		ln	T2	,	(4.17)
∆S = Cр		ln	T	,	(4.17)
			T
		1

где Т1 и Т2 – температуры начала и окончания нагревания

вещества.
Пусть Cр выражается в Дж/моль· К, тогда
∆S = n Cр ln	T2	,	(4.18)
	T

1

Пусть Cp выражается в Дж/г ·К, тогда

∆S = g Cр lnT2 .

Если Cp зависит от температуры, т.е. Cр = f (T), тогда

dS T2 (a bT cT2 с Т 2) dT . T

б) Пусть V = const, тогда

(4.19)

(4.20)

dS CV ln	T2
		.	(4.21)
	T
	1

Для расчёта абсолютного значения энтропии S вещество нагревается от абсолютного нуля до данной температуры ( p = const).

Для твёрдого тела при температуре T

S тв

C p (тв )

(4.22)

273

Для жидкости при температуре T

Tпл

Sж Cp (тв)

пл

Cp (ж)

(4.23)

273

пл

Для

газа

при

пл

температуре

Tпл

Tкип

Sг Cp(тв)

пл

Cp(ж)

исп

Cp(г)

(4.24)

273

пл

Tпл

кип

Tкип

Задача.

Найти изменение энтропии g кг воды (тв.) Н2О при нагревании (охлаждении) в интервале температур от Т1 до Т2, если известны температуры плавления и кипения, средние теплоемкости, теплоты плавления и испарения.

Таблица 3

Термодинамические величины веществ

g,	Т1,	Т2,	Плавление							Испарение						Удельная теплоемкость,
кг	К	К																	Дж/кг·К
			Т ,		Нпл	10	3	,	Т	исп..		Нпл		3	С	тв	10	3	ж	10	3	г	10	3
			пл		Нпл	10		,		исп..		Нпл	10,		С	р	10		Ср	10		Ср	10
			К	Дж/моль					(Ткип.),		Дж/моль
										К
2,	25	37	273,	6,138					373,2		45,069				0,570				4,187			1,919
7	3	9	2

Решение.

1) Представим процесс нагревания вещества от Т1 и Т2 по стадиям:

от Т1 от Тпл

1 стадия. Твердое вещество (при Т1)

Tпл Ствр

нагревание

g Ств

2,7 0,570 103

273,2

S g

2,303 lg

пл

2,303

Т1

253

118,39( Дж К 1 ).

2 стадия. Твердое вещество (при Т

)

пл.

плавление

Нпл.

2,7

6,138

3370(Дж К 1).

Тпл.

18 10 3

273,2

от Тпл от Ткип

3 стадия. Жидкость (при Тпл.)

TкипСрж dT

нагревание

g Сжр

исп.

S3 g

2,303 lg

кип.

Тпл

Тпл.

2,7 4,187 103

2,303 lg

273,2

3526,8( Дж К 1 ).

273,2

испарение

4 стадия. Жидкость (при Ткип.)

кипение

исп.

2,7

45,069 103

18114,5(Дж К 1)

273,2

Тисп.

18 10 3

5 стадия. Пар (при Ткип.)

отТкrип

от Т2

Пар (при Т2)

нагревание

T2 С

рг dT

g Срг

379

S5 g

2,303 lg

2,7 1,919 103 2,303 lg

79,9(Дж К 1)

кип.

373,2

Ткип.

Находим изменение энтропии при нагревании вещества от Т1 до Т2.

S S1 S2 S3 S4 S5

25209,59 25,2(кДж/К).

Изменение стандартной энтропии системы S 298 при протекании химической реакции определяется как разность суммы стандартных энтропий продуктов и суммы стандартных энтропий исходных веществ.

Sо298 S 298(продуктов.реакции) S 298(исходных.веществ) (4.25)

Значения величин стандартных энтропий (определенных для стандартных условий) веществ приведены в справочниках.

Энтропия, как критерий возможности протекания процесса в

изолированной системе (U,V = const). Изолированная система не обменивается с окружающей средой теплотой, т.е. Q 0. Поэтому,

согласно второго закона термодинамики
(dS)U,V ≥ 0.	(4.26)
Необратимый процесс в изолированной системе возможен при
(dS)U,V > 0.	(4.27)
При равновесном состоянии системы (или обратимом процессе)
(dS)U,V = 0;	(4.28)
при этом энтропия принимает максимальное значение S = Smax.
Если (dS)U,V < 0	(4.29)

– необратимый процесс в изолированной системе неосуществим.

Л е к ц и я 5

ТЕРМОДИНАМИКА АГРЕГАТНЫХ ПРЕВРАЩЕНИЙ

План лекции: Уравнение Клайперона – Клаузиуса. Применение уравнения Клайперона – Клаузиуса к процессам испарения и возгонки. Зависимость давления насыщенного пара от температуры.

Фазовые переходы чистого вещества в двухфазной однокомпонентной системе представим следующим образом.

	Фазовый переход:		Процесс:		При фазовом переходе:
	α→β				значительно изменяется
	Жидкость	Пар	Испарение		значительно изменяется
					объем;
	Твердое	Пар	Возгонка		объем практически не
	Твердое	Жидкость	Плавление		объем практически не
					изменяется;
	Твердое	Твердое	Полиморфное		(конденсированное
			превращение		состояние).
При равновесии dG 0 или dG				dG .

При этом

dG V dp S dT,		(5.1)
dG	V dp S dT,	(5.2)

где V иV - это мольные объемы вещества в фазах α и β,

S иS - это энтропии вещества в фазах α и β.

Так как dG dG , получаем

dp S dT V

dp S

dT.

Объединяем объемы и энтропии:

S )dT (V V )dp.

(5.3)

Отсюда

(5.4)

где S иS

S - это изменение энтропии при фазовом переходе;

V и V

V - это изменение объема при фазовом переходе.

Так как

, получаем

dp H

(5.5)

T V

где

- изменение давления насыщенного пара с температурой.

Уравнение (5.5) - это уравнение Клаузиуса-Клайперона,

Применение уравнения Клаузиуса-Клайперона к процессам

испарения и возгонки.

переходит

«Жидкость пар» или

«твердое пар».

V Vпар Vж

или

V Vпар Vтв .

Vпар Vж

или

Vпар Vтв .

Объемом конденсированного состояния (жидкости, твердого) можно пренебречь по сравнению с объемом пара и считать: Vпар Vж .

Предложим, что пар подчиняется законам идеального газа, тогда

Подставляем

это

выражение

в уравнение (5.5):

, получаем:

H p

Так как

d ln p ,

dT T V

T R T

получаем

dln p	H	.	(5.6)
	2
dT	RT

Это уравнение Клаузиуса-Клайперона для процессов испарения и выгонки. Физический смысл уравнения: с ростом температуры давление насыщенного пара в системе растет.

При Н const можно из уравнения Клаузиуса-Клайперона найти значение величины теплового эффекта и равновесного давления насыщенного пара. Преобразуем уравнение (5.6), получаем

d ln p	H	dT	.	(5.7)
	R	2
		T

Берем неопределенный интеграл выражения (5.7), после интегрирования:

ln p	H	1	const.	(5.8)
		T
	R

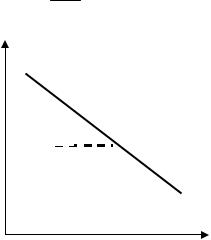
Уравнение (5.8) отвечает уравнению прямой линии. Построим графическую зависимость ln p f (1/T), рис. 2. Из графика находим

тангенс угла наклона α: tg R , тогда H Rtg .

lnp

1/Т

Рис. 2. Графическая зависимость

ln p f (1/T)

Возьмем определенный интеграл выражения (5.7), получаем:

	p2	H		1		1

ln	p	R			T			(5.9)
			T				.
	1			2	1

Л е к ц и я 6

ТЕРМОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ

План лекции: Термодинамический потенциал. Изохорноизотермический потенциал или свободная энергия Гельмгольца. Применение энергии Гельмгольца в качестве критерия направления самопроизвольного процесса и равновесия в закрытых системах. Изобарно-изотермический потенциал или свободная энергия Гиббса. Применение энергии Гиббса в качестве критерия направления самопроизвольного процесса и равновесия в закрытых системах. Характеристические функции: внутренняя энергия, энтальпия, свободная энергия Гельмгольца, свободная энергия Гиббса. Уравнения Гиббса-Гельмгольца. Химический потенциал.

Термодинамический потенциал – это функция состояния системы,

убыль которой в процессе, протекающем при постоянстве двух параметров, равна максимальной полезной работе.

Энергия Гельмгольца как изохорно-изотермический потенциал.

Для изохорно-изотермических условий V = const, T = const. Вспомним, что объединенное уравнение, выражающее первый и второй законы термодинамики, имеет следующий вид:

TdS dU pdV A .

Так как при V = const, pdV = 0, получим

				(6.1)
	A	dU TdS .
Проинтегрируем данное уравнение:
A (U2 U1) T(S2 S1),		A (U2 TS2 ) (U1 TS1) .
Введем обозначение F – это энергия Гельмгольца.
	F = U - TS			(6.2)
Тогда F2 = U2 - TS2 и F1 = U1 - TS1.
A	F2 F1 ,
		A (F2 F1) или	A	F.

То есть энергия Гельмгольца – это термодинамический потенциал, так как его изменение равно полезной работе при протекании обратимого процесса в системе. Для необратимого процесса: A F. В общем случае для обратимого и необратимого процессов справедливо выражение

	(6.3)
A F.

A G.

То есть энергия Гиббса G – это термодинамический потенциал, так как его изменение равно полезной работе при протекании обратимого процесса в системе. Для необратимого процесса В случае для обратимого и необратимого процесса справедливо выражение

(6.9)

Энергия Гельмгольца равна F U TS , отсюда
U = F+TS.	(6.4)

То есть F – это та часть внутренней энергии, которая может быть превращена в работу, поэтому она называется свободной энергией; произведение TS – это энергия, которая выделяется в виде тепла, поэтому она называется связанной энергией.

Энергия Гельмгольца как критерий возможности протекания процесса. Дифференцируя выражение F U TS получим dF = dU

– TdS - SdT . Подставляя вместо произведения TdS его выражение из

«объединенного» уравнения TdS ≥ dU+pdV	получим
dF ≤ - SdT - pdV.	(6.5)
Так как SdT = 0 и pdV= 0 (при Т = const	и V= const), тогда для
изохорно-изотермических условий
(dF)v,T ≤ 0.	(6.6)

В закрытых (замкнутых) системах при изохорно-ихотермических условиях:

если dF < 0, то процесс протекает самопроизвольно;

если dF > 0, то процесс не протекает;

если dF = 0, то система находится в состоянии равновесия.

Энергия Гиббса как изобарно-изотермичесий потенциал. Для

изобарно-изотермических условий р = const , T = const. Преобразуем объединенное уравнение первого и второго законов термодинамики:

TdS dU pdV A как A dU pdV TdS.		(6.7)
Проинтегрируем это выражение:
	V1) T(S2 S1) или
A (U2 U1) p(V2	V1) T(S2 S1) или

A (U2 pV2 TS2 ) (U2 pV1 TS1).

Введем обозначение
G U pV TS - это энергия Гиббса.				(6.8)
Тогда G2 U2 pV2	TS2 ,	G1 U1 pV1 TS1.
A G2 G1 ,	A (G2 G1),		A G.

Энергия Гиббса	равна G U pV TS		, но U pV H.
Поэтому
G H TS, отсюда		H G TS .		(6.10)
Энергия Гиббса G	– эта часть энтальпии,		которая может быть
превращена в работу; поэтому она называется свободной энергией.
В выражение для	энергии Гиббса G U pV TS			подставим
энергию Гельмгольца, которая определяется как F= U - TS. Тогда
получим, что
G F pV или		dG dF pdV .		(6.11)

Энергия Гиббса, как критерии возможности протекания процесса.

Продифференцируем выражение G U pV TS , получим dG dU pdV Vdp TdS SdT.

Вместо TdS подставим его значение из объединенного уравнения первого и второго законов термодинамики TdS dU pdV. Тогда dG dU pdV dU pdV SdT Vdp или

dG Vdp SdT.	(6.12)
В изобарно-изотермических условиях Vdp 0,SdT 0 и
(dG)p,T 0 .	(6.13)

То есть dG является критерием возможности протекания процесса в замкнутой (закрытой) системе в изобарно-изотермических условиях. При этом

если dG < 0, то процесс протекает самопроизвольно;

если dG > 0, то процесс самопроизвольно не протекает;

если dG = 0, то система находится в состоянии равновесия.

Характеристической функцией называется такая функция

состояния системы, посредством которой или ее производных могут быть выражены в явной форме термодинамические свойства системы. Характеристическими функциями являются:

1)внутренняя энергия U ,

2)энтальпия H,

3)изохорно-изотермический потенциал F,

4)изобарно-изотермический потенциал G,

5)энтропия S.

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.2021500.85 Кб1442.pdf
#
07.01.2021503.5 Кб0443.pdf
#
07.01.2021503.64 Кб0444.pdf
#
07.01.2021504.39 Кб19445.pdf
#
07.01.2021504.61 Кб17446.pdf
#
07.01.2021505.28 Кб1447.pdf
#
07.01.2021507.22 Кб4448.pdf
#
07.01.2021507.28 Кб0449.pdf
#
07.01.2021240.52 Кб145.pdf
#
07.01.2021508.25 Кб2450.pdf
#
07.01.2021508.5 Кб2451.pdf