
361
.pdfМинистерство образования РФ Сибирская государственная автомобильно-дорожная академия
(СибАДИ)
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
(Динамика)
Часть 1
Методические указания к выполнению расчетно-графических работ
по теоретической механике
Составитель Н. И. Фисенко
Омск Издательство СибАДИ
2004
УДК 531.01 ББК 22.21
Рецензент В.Н. Никитин, канд. техн. наук,
профессор кафедры «Детали машин» СибАДИ
Работа одобрена методической комиссией факультета ТТМ в качестве методических указаний для студентов всех факультетов, изучающих теоретическую механику.
Теоретическая механика. (Динамика): Методические указания к выполнению расчетно-графических работ потеоретической механике / Сост. Н.И.Фисенко. Омск: Изд-воСибАДИ, 2004. Часть1. 32с.
Методические указания предназначены для студентов дневных и заочных факультетов, изучающих теоретическую механику. Содержание отражает основной курс динамики и включает в себя решение задач, аналогичных заданиям выполняемых курсовых работ Д-1, Д-4, Д-15, Д-16 из «Сборника заданий» А.А.Яблонского. В соответствии с разбираемой темой дается теория, решается задача, выполняется обзор, классифицируются варианты задания по группам, приводится экзаменационная задача с решением.
Репетиторский подход и анализ решения задач призваны развивать логическое мышление студентов. Методические указания могут быть полезны студентам, изучающим сопротивление материалов и строительную механику, теорию механизмов и машин, детали машин, а также студентам старших курсов и аспирантам.
Ил. 15. Библиогр.: 6 назв.
С Издательство СибАДИ, 2004
Введение
Методические указания по динамике (I и II части) предназначены для студентов всех факультетов, выполняющих задания для курсовых работ в соответствии с Государственным образовательным стан-дартом и программой курса по теоретической механике. Эти указания отражают основной курс динамики, который включает в себя общие теоремы динамики и три основных принципа механики. На после-дующих курсах при изучении технических дисциплин "Детали машин" и "Теория механизмов и машин" широко используются эти фундаментальные методы, лежащие в основе расчетов различных механизмов и машин. Принцип возможных перемещений, излагаемый в заданиях Д-14 и Д-15, применяется для решения задач сопротив-ления материалов и строительной механики.
В методических указаниях выделены два основных метода расчета, основанных на втором законе Ньютона и принципе Даламбера, позволяющем показать силы инерции не в скрытом виде как параметры движения, а как реально действующие силы, направ-ленные противоположно соответствующим ускорениям. Силы инерции, например, в заданиях Д-1 и Д-4 позволяют объяснить движение с позиции статики с использованием уравнений равновесия.
Для каждой разбираемой темы кратко дается теория, приводится решение задачи, подобной сложному варианту задания, выполняются обзор и классификация вариантов задания по группам, решается экзаменационная задача.
Расчетно-графичесие работы оформляются на листах формата А-4 в соответствии с разобранными примерами выполнения заданий из сборника А.А. Яблонского и из данных методических указаний.
Методические указания помогут студентам самостоятельно решать задания, развивают логику технического мышления и содержат минимум необходимой информации.
1. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
Изучение динамики 2, 3, 4 начинается с трактовки четырех основных законов механики.
Первый закон инерции устанавливает свойство тел сохранять неизменной скорость их движения без воздействия других тел.
Второй закон Ньютона констатирует, что ускорение материальной точки пропорционально приложенной к ней силе и имеет одинаковое с ней направление.
Согласно третьему закону, всякому действию соответствует равное и противоположно направленное противодействие. Таким образом, силе, вызывающей ускорение точки, противодействует сила инерции точки.
Четвертый закон независимости действия сил часто приме-няется для решения задач и гласит, что несколько одновременно действующих сил сообщают точке такое ускорение, какое сообщила бы одна сила, равная их геометрической сумме.
Выделяются две задачи динамики: первая определение силы по заданному движению, вторая определение закона движения по заданным силам. Обе задачи решаются с помощью основного уравнения динамики
ma Fi и полученных на его основе дифференциальных уравнений движения:
|
, |
|
, |
|
mx Fix |
my Fiy |
mz Fiz . |
Первая задача динамики решается дифференцированием уравнений движения, а вторая интегрированием дифференциальных уравнений движения точки под действием заданных сил и с учетом начальных условий движения (начального положения и начальной скорости). В случае действия постоянных сил интегрирование производится методом разделения переменных величин.
Вторая задача динамики является более сложной, т.к. силы, входящие в правую часть уравнения, могут зависеть от времени, положения и скорости точки. Если в процессе движения силы изменяются, то для описания дальнейшего движения надо составить новые дифференциальные уравнения движения, начальными усло-виями которых будут скорость и положение точки в конце предшествующего движения.
1.1. Задание Д-1. Интегрирование дифференциальных уравнений движения материальной точки, находящейся
под действием постоянных сил

Рассмотрим пример движения лыжника по трамплину АВ и |
||||||
последующий его свободный полет на участке ВС (рис. 1). |
|
|||||
|
|
Y |
Ф |
|
|
|
|
|
|
|
|
|
|
|
|
|
Фn |
|
|
X1 |
|
N |
|
|
|
Ф |
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
Ф |
|
V |
а |
|
X |
|
|
В |
B |
|
|
|
|
а |
|
|
аn |
||
Y1 |
|
|
а |
|
||
Fтр |
|
|
|
|||
|
|
|
|
G |
|
|
|
А |
|
|
|
|
h |
|
G |
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
Рис.1 |
|
|
|
|
Дано: Лыжник со скоростью VA подходит к точке А участка |
||||||
трамплина АВ, имеющего длину l |
и угол наклона |
(относительно |
||||
горизонта). Коэффициент трения скольжения лыж на участке АВ равен f. |
||||||
Лыжник от А до В движется время , с; в точке В он покидает трамплин. |
||||||
Через T , с, лыжник приземляется со скоростью VС в точке С горы, |
||||||
составляющей угол наклона с горизонтом. При решении принять |
||||||
лыжника за материальную точку и не учитывать сопротивление воздуха. |
||||||
|
= 20 , |
|
= 0,5 с, |
|
|
|
|
VA = 20 м/с, |
VВ = 18 м/с, |
|
|
||
|
f = 0,1, |
= 45 |
. |
|
|
|
Определить l и d. |
|
|
|
|
|
|
Рассмотрим движение лыжника на участке АВ. Покажем действующие на лыжника силы: вес G, нормальную реакцию N и силу трения скольжения Fтр. Силой, движущей лыжника по трамплину, является сила инерции Ф, направленная противоположно его ускорению а, которое, в свою очередь, направлено вдоль трамплина от В к А, так как скорость движения уменьшается (VA = 20 м/с, VВ = 18 м/с). Эту силу

инерции Ф покажем штриховой линией, потому что она входит в дифференциальное уравнение движения, в его левую часть, как параметр движения mx1 .
Составим дифференциальное уравнение движения:
|
|
|
|
, |
|
mx1 F , |
или mx1 G sin Fтр |
||
|
|
ix1 |
|
|
где |
Fтр = N f, |
а N G cos , |
|
|
тогда |
|
mgsin f mg cos , |
|
|
mx1 |
|
|||
x1 (gsin f g cos ).
Рассчитаем выражение в скобках, это будет постоянное отрицательное число, обозначим его К, чтобы дальше решать задачу в общем виде.
x1 К , x1 Кt C1,
t2
x1 К 2 C1 t C2.
Этот результат получен интегрированием методом разделения переменных величин. Рассмотрим этот метод на примере:
|
|
dVx |
1 |
|
|
|
|
|
|
|
|
|
|
|
x1 K, |
|
K, |
dVx1 |
K dt, |
Vx1 |
Kt C1 . |
|
|
||||
|
dt |
|
|
|
|||||||||
|
dx1 |
Kt C , |
|
dx K t dt C |
dt, |
x K t2 |
C t C |
2 |
. |
||||
|
|
|
|||||||||||
|
dt |
1 |
|
1 |
|
1 |
|
1 |
2 |
1 |
|
||
Постоянные интегрирования С1 |
и С2 |
определяем по начальным |
|
||||||||||
условиям движения |
|
(НУД): |
t0 = 0, x1 VA, |
|
|
|
|
||||||
|
x1 0 . |
|
|
||||||||||
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
Составим уравнения, полученные при интегрировании для t = 0:
|
С1, |
x1 С2, |
то есть |
С1 VA, |
С2 0, |
||
x1 |
|||||||
0 |
|
|
0 |
|
|
|
|
тогда |
|
Кt VA, |
x1 К |
t2 |
VA t. |
|
|
2 |
|
||||||
x1 |
|
||||||
Для момента , когда лыжник покидает участок АВ,
|
VВ , |
xB l. |
x1 |
Окончательные уравнения для расчета искомых параметров:
V |
В |
Kt V |
A |
, |
(1) |
|||
|
|
|
|
|
|
|
||
|
|
|
t |
2 |
|
|
|
|
|
|
|
|
|
|
|
||
l K |
|
V |
A |
t. |
(2) |
|||
|
|
|||||||
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
|||
Здесь неизвестные величины t и l. Выразим t из уравнения (1) и, подставив его в уравнение (2), определим l.
Рассмотрим движение лыжника на участке ВС свободное падение под действием только силы тяжести G. Чтобы пояснить, почему лыжник летит вверх и вправо по параболе, а не падает сразу вниз, покажем движущие его силы инерции: Фn нормальная и Ф касательная, противоположные соответствующим ускорениям. В дифференциальные уравнения движения они как силы не входят, поэтому покажем их штриховыми линиями.
Движение лыжника в плоскости YВХ описывается двумя дифференциальными уравнениями:
mx 0, my G.
Начальные условия движения на участке ВС:
|
|
VB cos , |
|
x0 0, |
|
НУД: t0 = 0, |
x0 |
|
|||
|
VB sin . |
y0 |
0. |
||
|
y0 |
|
|||
Сократим полученные дифференциальные уравнения на массу m.
x 0,
y G.
Интегрируем дважды эти уравнения |
|
|
|
|
|
, |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y gt C4 |
|
|
||||||
|
С3, |
|
|
|
|
|
|
t2 |
|
|
|
|
|||
|
x |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y С3t С5. |
|
y g |
|
|
C |
t C |
. |
|||||||
|
|
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
6 |
|
|
Напишем полученные уравнения для t = 0: |
|
|
|
|
|||||||||||
|
|
|
|
|
С3, |
|
|
|
|
, |
|
|
|||
|
|
|
x0 |
|
y C4 |
|
|
||||||||
|
|
|
x |
0 |
С |
. |
|
|
y C |
. |
|
|
|||
|
|
|
|
5 |
|
|
|
|
|
|
6 |
|
|
|
|
отсюда |
C3 VB cos , |
C4 VB sin , |
|
||||||||||||
|
C |
5 |
0. |
|
|
|
C |
6 |
0. |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Окончательные выражения скорости и пути в функции времени:
|
cos , |
(3) |
x VB |
||
x VB cos t, |
(4) |
|
|
|
|
|
|
|
(5) |
||||||
|
y gt VB sin , |
|||||||||||
y g |
t2 |
V |
B |
sin t. |
(6) |
|||||||
2 |
||||||||||||
|
|
|
|
h |
|
|
|
d |
|
|||
В момент падения y = h, |
x = d, при угле = 45 |
|
|
. Неизвестны |
||||||||
величины t и d. Для определения d выразим t через d из уравнения (4) и подставим его значение в уравнение (6).
1.2. Обзор и классификация вариантов задания Д-1
Отличительной особенностью задания Д-1 от других заданий является то, что здесь представлено 6 схем, а не 30 и для каждой схемы дано общее условие для пяти вариантов. Внутри схем варианты отличаются между собой только вариацией исходных данных и определяемых величин. Все схемы имеют два участка движения прямолинейный АВ и участок движения в плоскости.
Оба участка связаны общей скоростью VB, которая является конечной
скоростью для участка АВ и начальной скоростью для последующего участка ВС. В ряде вариантов скорость VB определяется из расчета
движения на участке ВС, а затем она подставляется в данные участка АВ. Схема 3 отличается от остальных схем наличием движущей силы силы тяги мотоцикла, тогда как в других вариантах движущая сила либо составляющая силы тяжес-ти, либо сила инерции.
Путем введения начальной скорости учитывается действие сил до начального расчетного момента движения на рассматриваемом участке. Для каждого участка свои действующие силы и соот-ветствующие им дифференциальные уравнения движения и начальные условия движения. Принципиально все варианты задания Д-1 не отличаются между собой
и решаются по единому алгоритму. Полученные дифференци-альные уравнения дважды интегрируются для определения скорости движения и пути в функции времени, то есть решается вторая задача динамики точки. Действующие силы постоянны, и поэтому интегрирование выполняется методом разделения переменных величин. Постоянные интегрирования определяются по начальным условиям движения. В ряде вариантов для определения искомых величин приходится совместно решать систему уравнений для первого и второго участков движения.
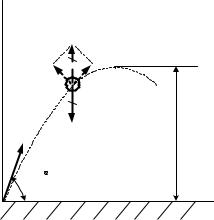
1.3. Задача по Д-1 6
Материальная точка М движется в вертикальной плоскости под действием силы тяжести (рис. 2). Определить
Y |
|
Ф |
|
|
|
Ф |
|
|
Фn |
|
|
V |
0 |
G |
max |
|
|
|
h |
О |
70 |
|
|
|
|
|
|
|
|
|
X |
максимальную высоту подъема h в км, если в начальный момент скорость
точки V0= 600 м/с. Вектор V0 расположен к горизонту под углом 70 .
V0= 600 м/с.
___________________
hmax ?
Решение.
Движение точки по параболе вверх и вправо происходит за счет сил
инерции Фn и Ф , показанных штриховыми линиями, однако при решении задачи с помощью диф-ференциальных уравнений движе-ния учитывается только сила тя-жести, так как силы инерции «спря-таны» в левых частях дифференциальных уравнений.
Составим дифференциальное уравнение движения, выбрав вертикальную ось Y и горизонтальную
ось Х , проведенные из начала движенияточки О со скоростью V0. Тогда
начальные условия движения:
|
|
|
|
t0 0, |
x0 0, y0 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
x0 V0 cos70 , |
y0 V0 sin70 . |
|
|
||||||||||||||||
|
|
Преобразуем и проинтегрируем дважды эти уравнения |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x C1t C3, |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
x С , |
|
|
|
|
|||||||||||
|
|
|
mx 0, |
mx 0, |
|
|
|
1 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
my G, |
my g, |
|
y gt С2, |
|
y g |
|
|
C |
t C |
4 |
. |
||||||||
|
|
|
|
|
|
2 |
|||||||||||||||||
|
|
Определим постоянные интегрирования: |
|
|
|
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
С1 = V0 cos70 = 205,2; |
С3 = 0; |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
С2 = V0 sin70 = 563,8; |
С4 = 0. |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
205,2; |
|
|
|
|
|
|
|
|
|
|
(7) |
||
Тогда |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(8) |
|||||
|
|
|
|
|
|
|
|
|
y 9,81t 563,8. |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
x 205,2 t; |
|
|
|
|
|
|
|
|
(9) |
|||||
|
|
|
|
|
|
|
|
y |
9,81 |
t |
2 |
563,8 t. |
|
|
|
|
|
|
(10) |
||||
|
|
|
|
|
|
|
|
|
2 |
|
dy |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Когда точка находится на максимальной высоте, то |
|
0, |
|
но |
|||||||||||||||||
|
|
|
dx |
|
|||||||||||||||||||
|
dy |
|
dy |
dt |
|
|
dt |
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
dx 0, |
где |
|
|
0, следовательно, |
|
y 0. |
|
|
|
|
|||||||||
|
dx |
dt |
|
dx |
dt |
|
|
|
|
||||||||||||||
Для определения t приравняем к нулю y в уравнении (8).
0 = 9,81 t +563,8; t = 57,47 с.
Для определения hmax= Ymax подставим значение t в уравнение(10).
Ymax = 4,9 57,47 2 + 563,8 57,47 = 16205 м = 16,2 км.
2. ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
Для вывода основного уравнения динамики относительного движения точки используется основное уравнение динамики абсолютного движения
точки: ma Fi .
Абсолютное ускорение точки a равно геометрической сумме относительного, переносного и кориолисова ускорений:
a ar aе aс .
Подставим эти ускорения в основное уравнение динамики, оставив в левой его части m ar , остальные слагаемые перенесем в правую часть со
знаком минус: m ar Fi maе maс. |
|
Обозначив переносную фе maе и кориолисову |
фс maс силы |
инерции, получим основное уравнение динамики относительного движения точки.
m ar Fi фе фс.
Из этого уравнения видно, что на относительное движение точки влияют не только действующие силы, но и переносное движение точки вместе с подвижной системой. Для решения задач используются дифференциальные уравнения относительного дви-жения точки, которые получаются при проецировании векторов на оси декартовых координат.
mx Fix Фex Фсx,
my Fiу Фey Фсy,
mz Fiz Фez Фсz.
В задании Д-4 относительным является прямолинейное движение точки по каналу, принадлежащему подвижной системе. Здесь требуется определить закон относительного движения точки xr f (t), то есть
решить вторую задачу динамики точки.
В зависимости от действующих сил в ряде вариантов надо решать однородные или неоднородные дифференциальные уравнения.
2.1. Задание Д-4. Исследование относительного движения материальной точки 1
