Иерархия хомского

Вернемся к определению грамматики как четверки вида G = (N, , P, S), где нас интересует вид правил P, под которыми понимается конечное подмножество множества

(N)^*N(N)^*(N)^*

В зависимости от конкретики реализаций правил P существует следующая классификация грамматик (в порядке убывания общности вида правил):

Грамматика типа 0:Правила этой грамматики определяются в самом общем виде.

P: xUyz

Для распознавания языков, порожденных этими грамматиками, используются т.н. машины Тьюринга – очень мощные (на практике практически неприменимые) математические модели.

Грамматика типа 1:Контекстно-зависимые (чувствительные к контексту)

P: xUyxuy

Грамматика типа 2:Контекстно-свободные. Распознаются стековыми автоматами (автоматами с магазинной памятью)

P: Uu

Грамматика типа 3:Регулярные грамматики. Распознаются конечными автоматами

P: Ua или UaA

При этом приняты следующие обозначения:

u  (N)⁺

x, y, z  (N)^*

A,U  N

a  

Условно иерархию Хомского можно изобразить так:

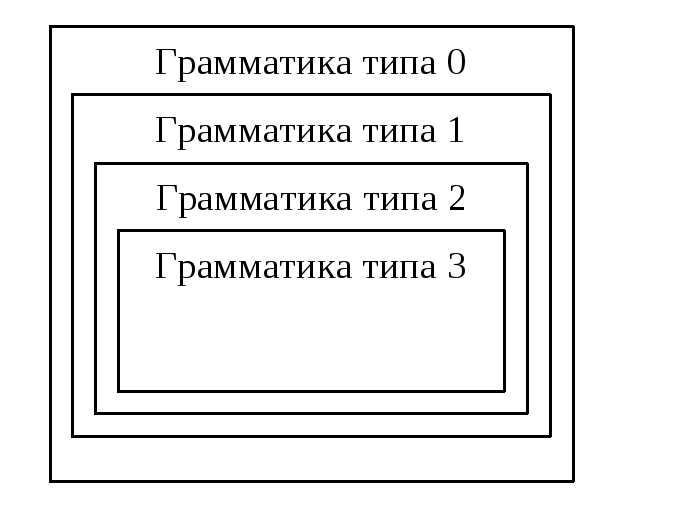
Итак, иерархия Хомского необходима для классификации грамматик по степени их общности. При этом, как видно,

• Грамматика типа 0 – самая сложная, никаких ограничений на вид правил в ней не накладывается.

• Грамматика типа 1 – контекстно-зависимая; в ней возможность замены цепочки символов может определяться ее (т.е. цепочки) контекстом.

• Грамматика типа 2 – контекстно-свободная; в левой части нетерминалы меняются на что угодно.

• Грамматика типа 3 – регулярная грамматика, самая ограниченная, самая простая.

Регулярные грамматики

Начнем изучение грамматик с самого простого и самого ограниченного их типа – регулярных грамматик. Вот некоторые примеры:

1. Идентификатор (в форме БНФ)

<идент> ::= <бкв>

<идент> ::= <идент><бкв>

<идент> ::= <идент><цфр>

<бкв> ::= a|b|...|z

<цфр> ::= 0|1|...|9

2. Арифметическое выражение (без скобок)

G = (N, ,P,S)

N={S,E,op,i}

={<число>, <идент>,+,-,*,/}

P={Si

SiE

Eop S

op+

op-

op*

op/

i<число>

i<идент>}

Ту же грамматику бесскобочных выражений можно изобразить в виде БНФ (это не совсем строго, зато весьма наглядно):

<expr> ::= <число>|<идент>

<expr> ::= <expr><op><expr>

<op> ::= +|-|*|/

<число> ::= <цфр>

<число> ::= <число><цфр>

3. Еще один пример:

Z ::= U0 | V1

U ::= Z1 | 1

V::=Z0 | 0

Порождаемый этой грамматикой язык состоит из последовательностей, образуемых парами 01 или 10, т.е. L(G) = {Bⁿ|n> 0}, гдеB= { 01, 10}.

Стоит, однако, рассмотреть чуть более сложный объект (например, арифметические выражения со скобками), как регулярные грамматики оказываются слишком ограниченными:

4. Арифметическое выражение (со скобками)

G₀=({E,T,F},{a,+,*,(,),#},P,E)

P = { E  E+T|T

T  T*F|F

F  (E)|a}

Это, разумеется, уже не регулярная, а контекстно-свободная грамматика.

Тем не менее, регулярные грамматики играют очень важную роль в теории компиляторов. По крайней мере, их достаточно для того, чтобы реализовать первую часть компилятора – сканер. Ведь сканер имеет дело именно с такими простыми объектами, как идентификаторы и константы.

Итак, будем считать, что мы как минимум умеем порождать фразы регулярных языков. Однако все-таки нашей основной задачей является не порождение, а распознаваниефраз. Поэтому далее рассмотрим один из наиболее эффективных распознающих механизмов – конечный автомат.