
- •НАГЛЯДНОЕ РЕШЕНИЕ ЗАДАЧ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ ИЗ РАБОЧЕЙ ТЕТРАДИ
- •Практикум № 1. Точка, прямая, плоскость на
- •Практикум № 2. Взаимное расположение геометрических элементов.
- •Практикум № 3. Перепендикулярность прямых и плоскостей.
- •Практикум № 4. Способы преобразования комплексного чертежа.
- •Практикум № 5. Поверхности, их образование и задание на чертеже.
- •Практикум № 6. Позиционные задачи. Развертка поверхностей.
- •Практикум № 7. Позиционные задачи. Пересечение поверхностей плоскостью и прямой линией.
- •Практикум № 8. Взаимное пересечение поверхностей.
- •Практикум № 9. Особые случаи пересечения
- •остроить комплексный чертеж прямой АВ по координат
- •Построить комплексный чертеж треугольника АВС по координатам его вершин А (0, 20, 10),
- •Построить следы прямой a и указать октанты, через
- •Построить следы прямой b и указать октаны, через которые она проходит.
- •10. Построить фронтальный след плоскости ABC. Выделить цветным карандашом след, находящийся в 1-ом
- •11. Построить горизонтальный след плоскости Σ (a ∩ b).
- •12. Определить координаты точки приземления B парашютиста, если скорость снижения – вектор AB,
- •20. Определить взаимное положение прямой l и плоскости Г(a ∩ b).
- •21. Определить взаимное положение прямой l и плоскости Г(f0 ∩ h0).
- •Определить взаимное положени плоскостей ABC и DEF, видимость
- •Определить взаимное положение
- •Задача 24
- •Задача 24
- •Задача 24
- •Задача 24
- •№26 Из точек А, В, С опустить перпендикуляры на соответст- вующие им на
- •№27 Провести перпендикуляр к плоскости из т.D принадлежа- щей АВС.
- •№28 Опустить перпендикуляр из т.А На плоскость заданной
- •№29 Через прямую АВ провести плоскость перпендикулярную плоскости F(a || b).
- •№30 Изобразить направление движения шара, скатывающегос с наклонного щита ВDСЕ, и определить угол
- •Определение натуральной величины прямых AS и BS и угла наклона между ними.
- •Чтобы прямые стали прямыми уровня вводим дополнительную плоскость проекции П4 : X1 ║
- •Из точек A1 и B1 проводим линии связи
- •Спроецируем точки A,B,S, в плоскость П4
- •Соединяем точки A4 с S4 и B4 с S4. Угол, между прямыми A4S4
- •Нужно построить горизонталь h
- •Из точек B 1,C1, D1 проводим линии связи
- •DK – искомое расстояние
- •Определение угла наклона между двумя пересекающимися прямыми AB и BC.
- •Определение кратчайшего расстояния между траекториями полета двух самолетов.
- •На прямых a и b произвольно отметим точки Спроецируем эти точки в плоскость
- •Через точки A1, A′1, B1, B′1 проведем линии связи.
- •Спроецируем точки B и B′
- •Соединяем точки B5 и B′5
- •РАБОТА №37
- •РАБОТА №38
- •Задача № 39
- •№39 1) Строим фронтальную проекцию горизонтали h2, плоскости ABC. Находим точку её пересечения
- •№39 2) Строим горизонтальную проекцию горизонтали h1. Находим точку 11, пересечения h1 со
- •№39 3) Введем дополнительную плоскость
- •Задача № 40.
- •№40 1) Построим фронтальные проекции фронталей f1, f’1, f”1.. Они параллельны, так как
- •№40 2)Строим фронтальные проекции фронталей..
- •Задача 41
- •Задача 41 Условия задачи:
- •Задача 41
- •Задача 41
- •Задача 41
- •Задача 41
- •Задача 41
- •Задача 41
- •Задача 41
- •Задача 41 Результат решения
- •Задача 42
- •Задача 42
- •Задача 42
- •Задача 42
- •Задача 42
- •Задача 42
- •Задача 42
- •Задача 42
- •Задача 42
- •Задача 42
- •Задача 42
- •Задача 42 Результат решения
- •Задача 43
- •Задача 43
- •Задача 43
- •Задача 43
- •Задача 43
- •Задача 43
- •Задача 43
- •Задача 43
- •Задача 43
- •Задача 43
- •Задача 43
- •Задача 43
- •Задача 43
- •Задача 43
- •Задача 43
- •Задача 43
- •Задача 43
- •Задача 43
- •Задача 43
- •Задача 43
- •Задача 43
- •Задача 43
- •Задача 44
- •Задача 44
- •Задача 44
- •Задача 44
- •Задача 44
- •Задача 44
- •Задача 44
- •Задача 44
- •Задача 44
- •Задача 44
- •Задача 44
- •Задача 44
- •Задача 44
- •Задача 44
- •Задача 44
- •Задача 44
- •Задача 44
- •Задача 44
- •Задача 44
- •Задача 44
- •Задача 44
- •Задача 44
- •Задача 44
- •Задача 44
- •Задача 44
- •Задача 45
- •Задача 45
- •Задача 45
- •Задача 45
- •Задача 45
- •Задача 45
- •Задача 45
- •Задача 45
- •Задача 45
- •Задача 45
- •Задача 45
- •Задача 45
- •Задача 45
- •Задача 45
- •Задача 45
- •Задача 45
- •Задача 45
- •Задача 45
- •Задача 45
- •Задача 45
- •Задача 45
- •Задача 45
- •Задача № 47
- •Задача №49
- •Задача №49
- •Задача №49
- •Задача №49
- •Задача №49
- •Задача №49
- •Задача №50
- •Условие задачи: построить проекции и натуральную величину сечения пирамиды плоскостью
- •Задача №50
- •Задача №51
- •Задача №51
- •Задача №51
- •Задача №51
- •Задача №51
- •Задача №51
- •Задача №52
- •Задача №52
- •Задача №52
- •Задача №52
- •Задача №52
- •Задача № 53
- •Решение задачи № 53
- •Задача № 54
- •Задача № 54
- •Решение задачи 54а:
- •Решение задачи 54б:
- •Решение задачи 54в:
- •Решение задачи 54г:
- •Задача № 55
- •Задача № 56
- •Будет ли виден самолет (точка
- •Построить линию пересечения цилиндра и конуса.
- •Задача
- •63. Построить линию пересечения конуса и сферы.
- •1. Строим вспомогательные секущие плоскости.
- •Строим точки пересечения поверхностей.
- •Строим саму линию пересечения.
- •64. Построение линии пересечения конуса и цилиндра.
- •1.Строим вспомогательные плоскости уровня.
- •2.Строим линию пересечения, замеряем r, на фронтальной проекции и делаем засечки на соответствующих
- •Строится искомая линия пересечения.
- •65. Построить линию пересечения конуса и цилиндра.
- •Искомую линию пересечения находим согласно теореме Монжа:
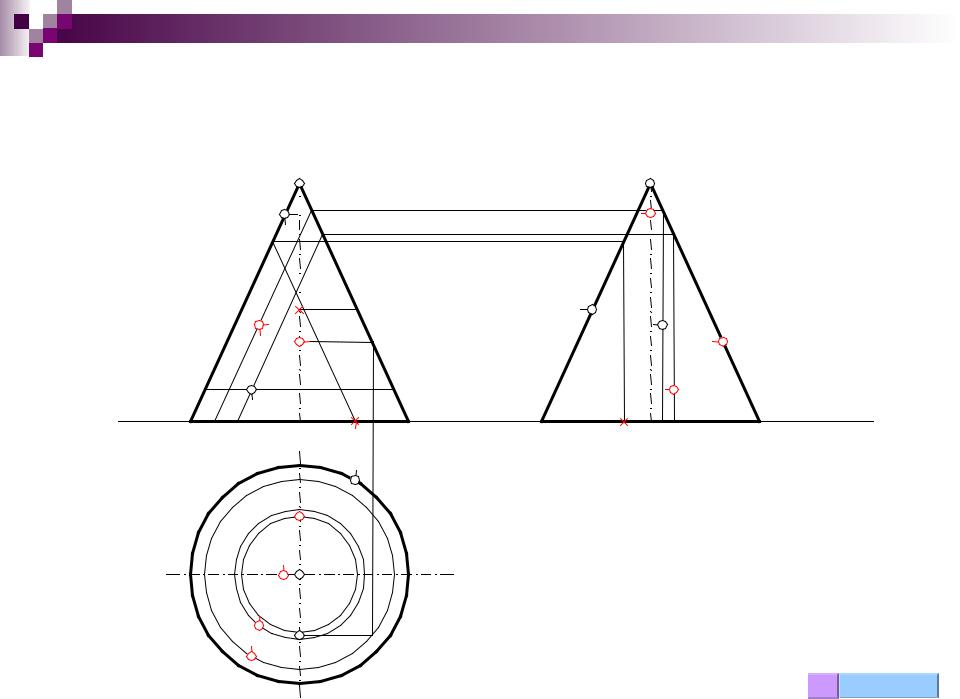
Задача 45
Аналогично тому как мы находили проекцию В1 точки В находим проекцию F1
X
S
A 2
2
2
k E
E
F 2 |
l2 |
2 q |
|
||
2 |
|
C |
2 |
|
|
|
B |
|
|
||
|
2 |
|
|
||
|
|
|
|
D |
|
|
2 |
|
O |
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
D |
|
|
|
|
|
1 |
|
|
E |
|
|
|
|
|
1 |
S1 ≡ |
|
|
|
A |
O1 |
|
||
F |
1 |
C |
|
|
|
B |
|
1 |
|
|
|
1 |
|
|
|
||
|
|
|
|
|
|
|
1 |
|
|
|
|
S3
|
|
A |
|
|
|
|
3 |
|
|
E |
k |
F |
|
|
3 |
C |
|||
q 1 |
l31 |
|||
|
3 |
|||
|
1 |
B |
|
3
D O
33

 Главное меню
Главное меню
A' |
B' |
C' |
2 |
2 |
2 |
|
2 |
|
|
M |
|
П2 |
A |
|
B |
C |
П1 |
A' |
|||
2 |
1 |
2 |
2 |
|
|
|
|
|
 C'1
C'1
 B'1
B'1
A1



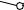
 C1
C1
B1
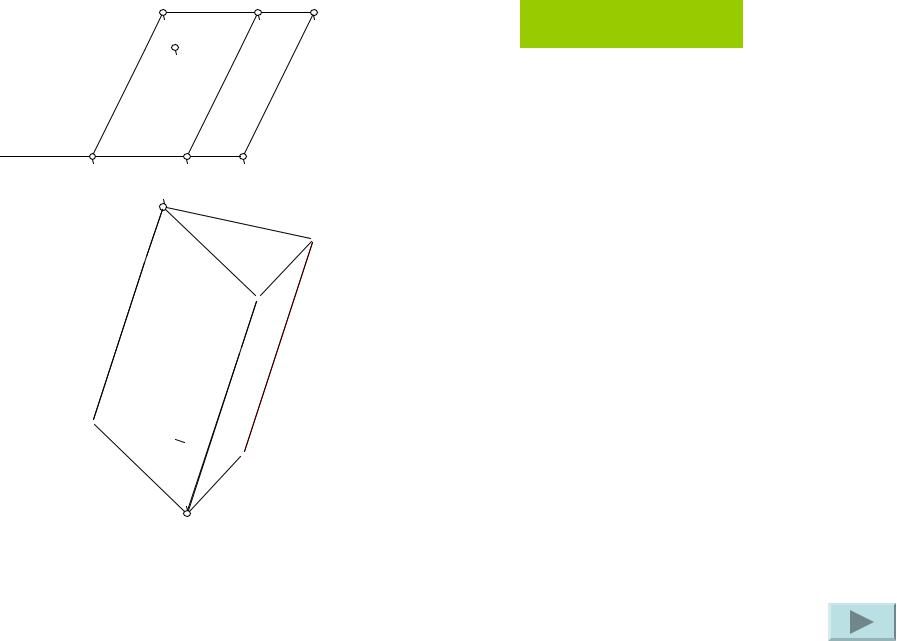
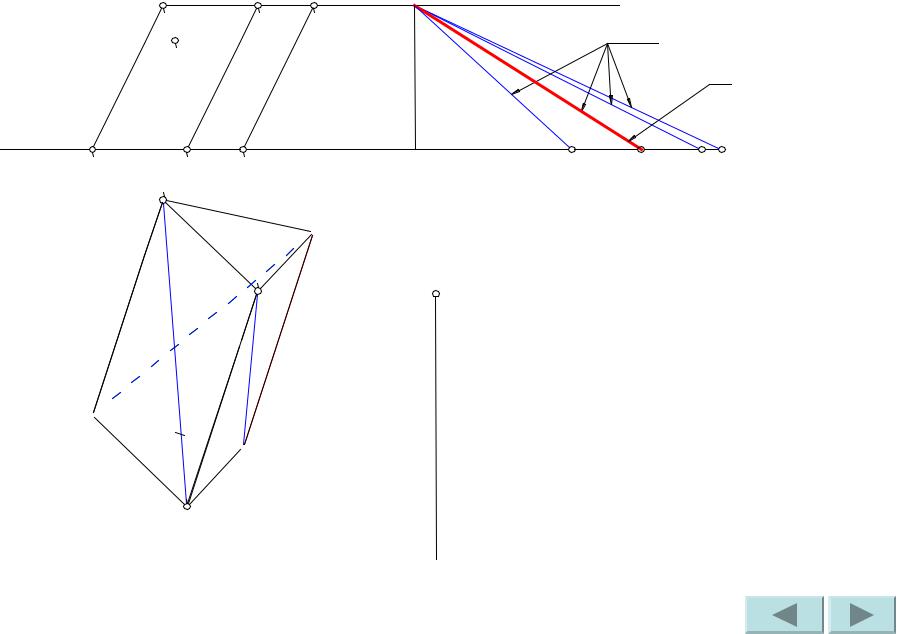
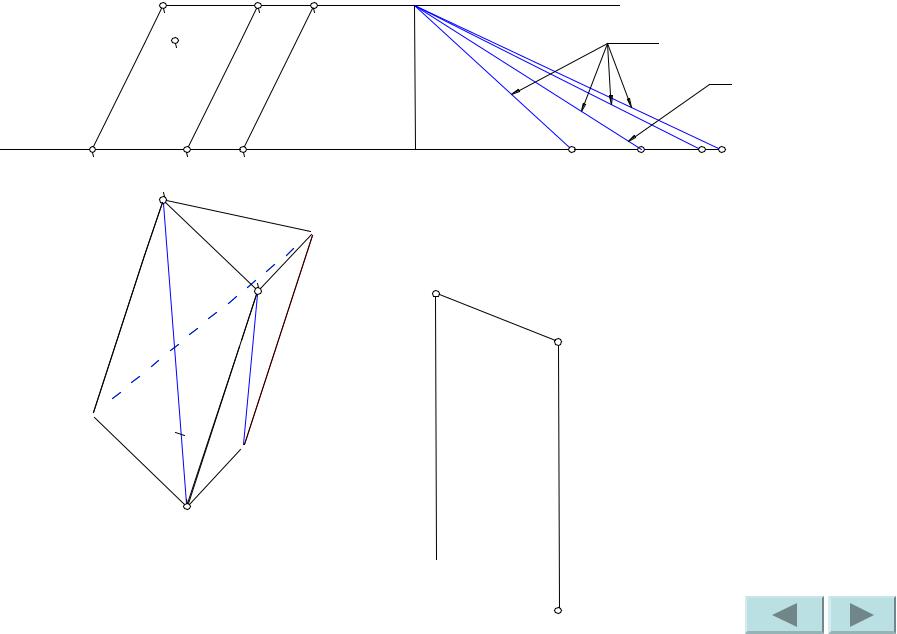
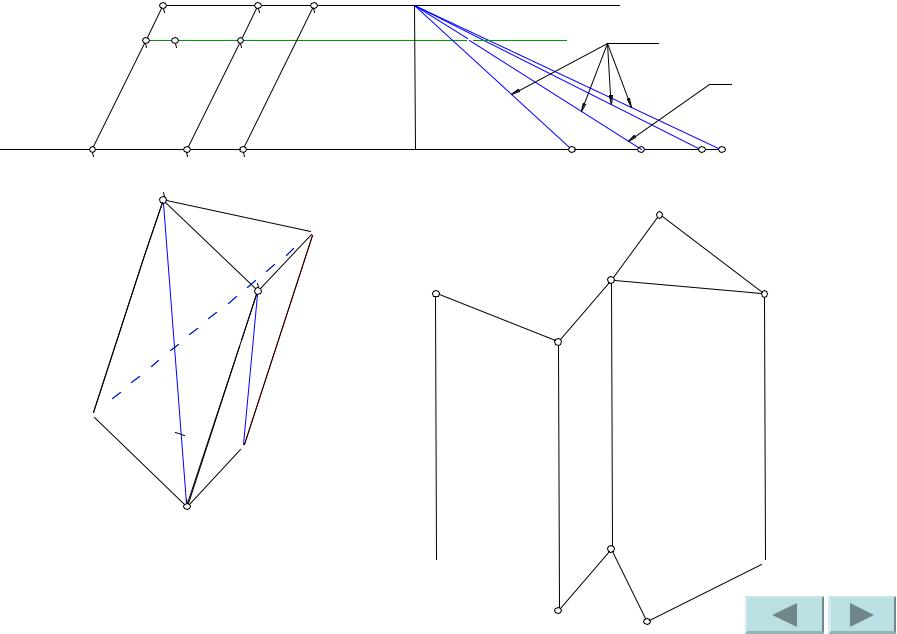
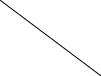
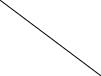
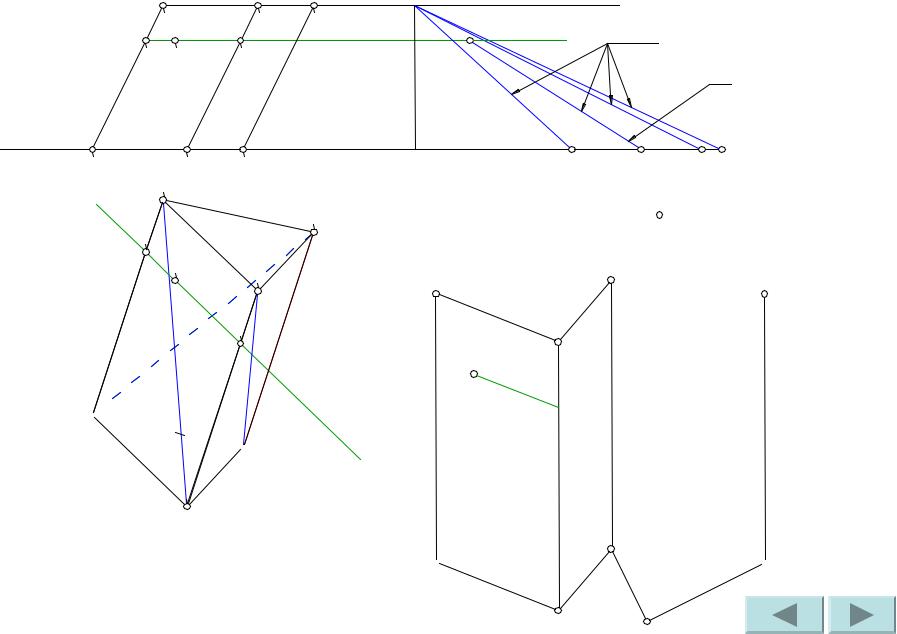
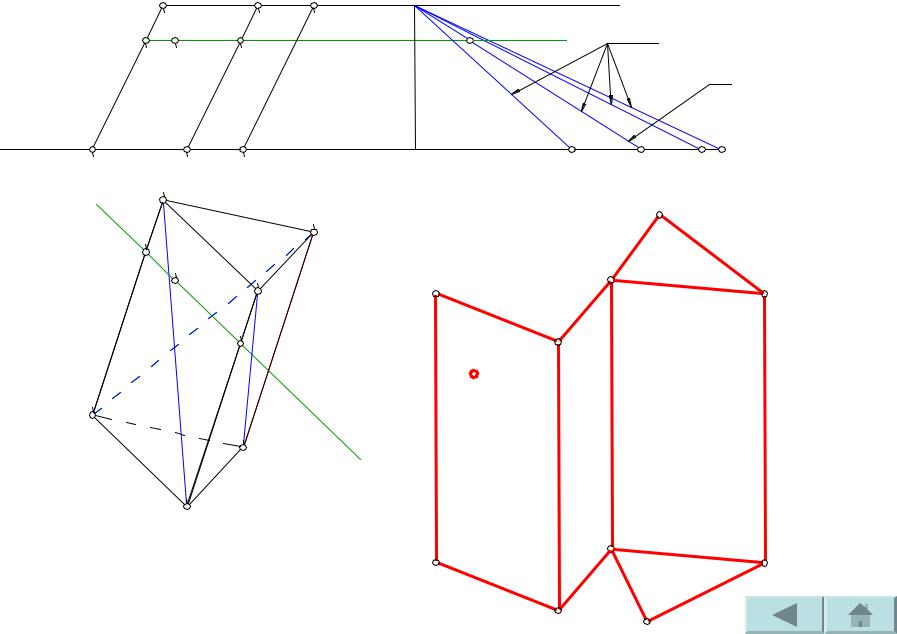
Задача №46
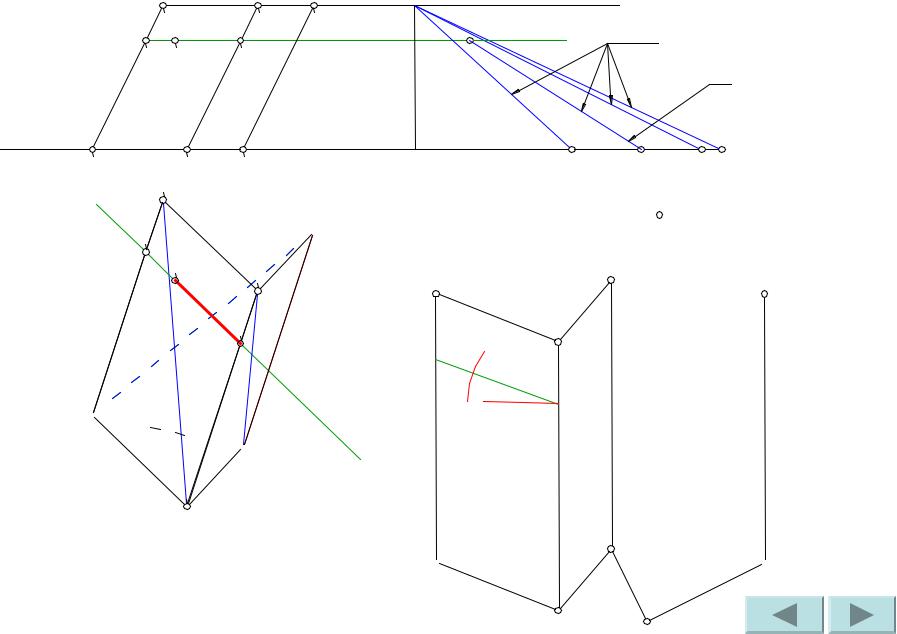
Построить развертку наклонной призмы. На развертке определить положение точки M, принадлежащей видимой грани.
A' |
B' |
C' |
2 |
2 |
2 |
|
2 |
|
|
M |
|
П2 |
A |
|
B |
C |
П1 |
A' |
|||
2 |
1 |
2 |
2 |
|
|
|
|
|
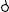 C'1
C'1
 B'1
B'1
A1



 C1
C1
B1
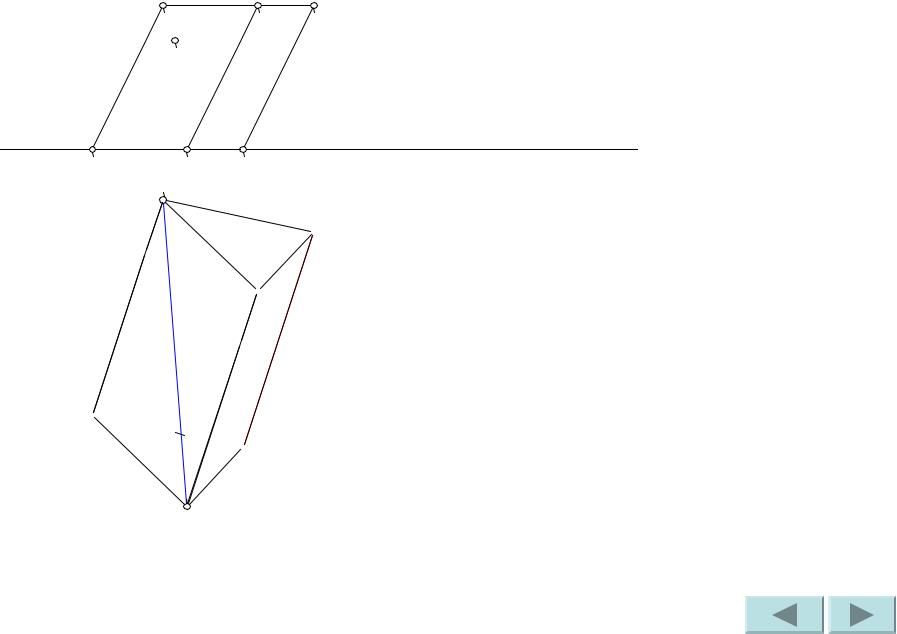
Дано: фронтальная и горизонтальная проекции наклонной призмы, фронтальная проекция точки M,
принадлежащей грани AA’B’B.
A' |
B' |
C' |
Построим диагональ A’1B1. |
2 |
2 |
2 |
|
|
2 |
|
|
|
M |
|
|
П2 |
A |
|
B |
C |
П1 |
A' |
|||
2 |
1 |
2 |
2 |
|
|
|
|
|
 C'1
C'1
 B'1
B'1
A1



 C1
C1
B1
A' |
B' |
C' |
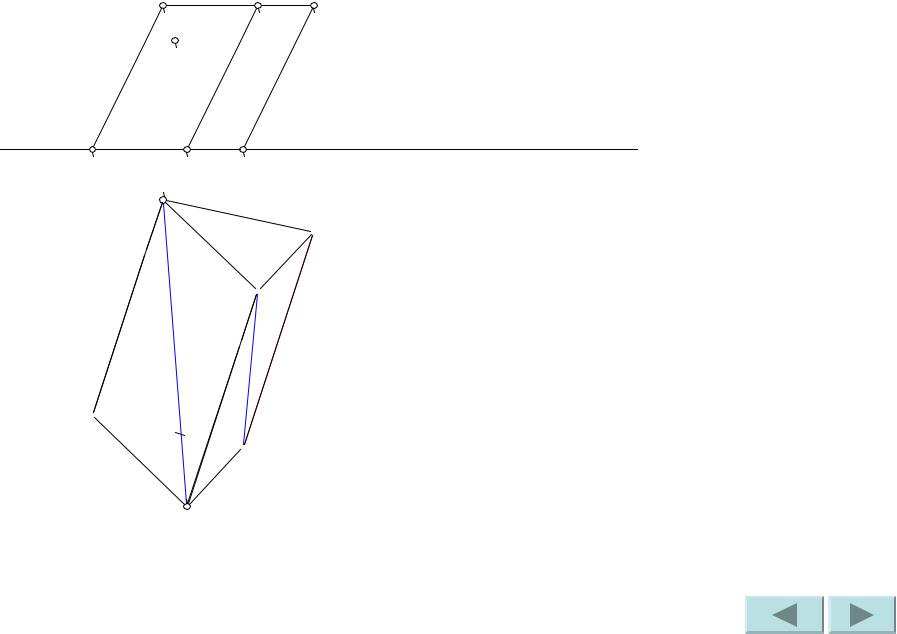
Построим диагональ B’1C1. |
2 |
2 |
2 |
|
|
2 |
|
|
|
M |
|
|
П2 |
A |
|
B |
C |
П1 |
A' |
|||
2 |
1 |
2 |
2 |
|
|
|
|
|
 C'1
C'1
 B'1
B'1
A1



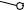
 C1
C1
B1
A' |
B' |
C' |
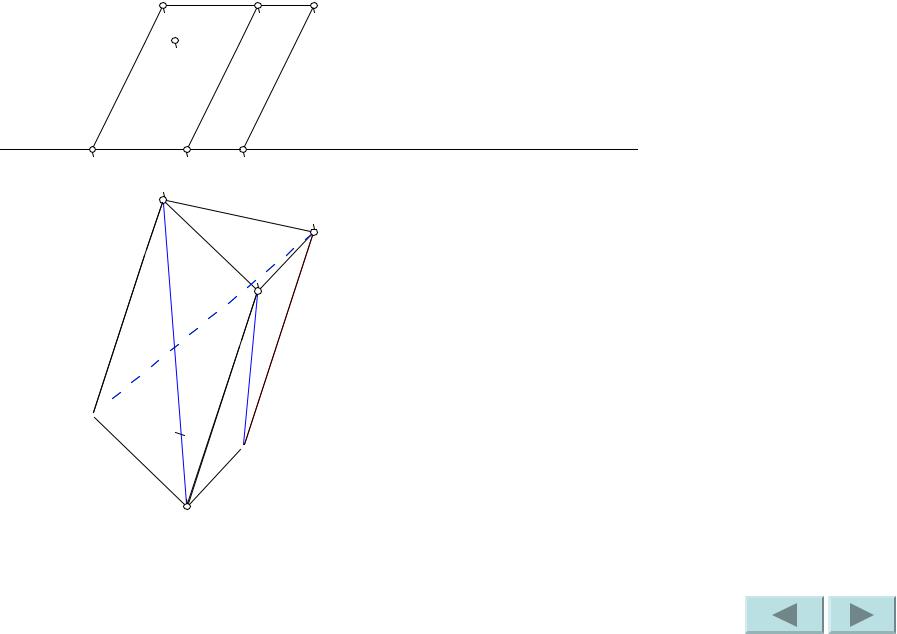
Построим диагональ C’1A1. |
2 |
2 |
2 |
|
|
2 |
|
|
|
M |
|
|
П2 |
A |
|
B |
C |
|
A' |
|||
П1 2 |
1 |
2 |
2 |
|
|
|
|
C' |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
B'1 |
|
|
|
|
|
|
|
|
|
|
A1



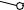
 C1
C1
B1
A' |
B' |
C' |
2 |
2 |
2 |
|
2 |
|
|
M |
|
П2 |
A |
|
B |
C |
|
A' |
|||
П1 2 |
1 |
2 |
2 |
|
|
|
|
C' |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
B'1 |
|
|
|
|
|
|
|
|
|
|
A1



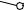
 C1
C1
B1
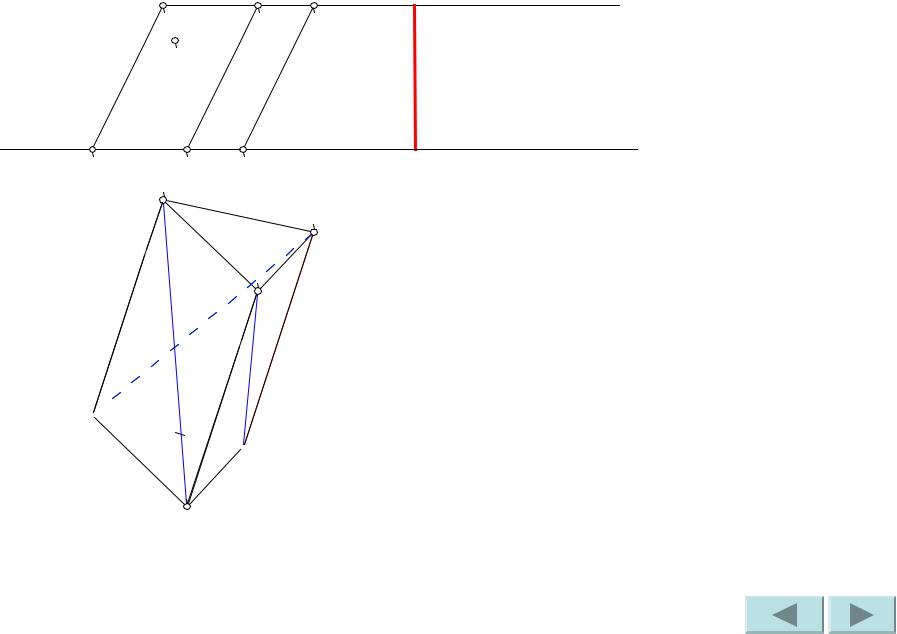
Найдем натуральную величину диагоналей и ребер способом прямоугольного треугольника. Построим 1-ый катет, равный разности координат концов отрезков диагоналей и ребер на фронтальной плоскости проекций.
A' |
B' |
C' |
2 |
2 |
2 |
|
2 |
|
|
M |
|
П2 |
A |
|
B |
C |
|
A' |
|||
П1 2 |
1 |
2 |
2 |
|
|
|
|
C' |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
B'1 |
|
|
|
|
|
|
|
|
|
|
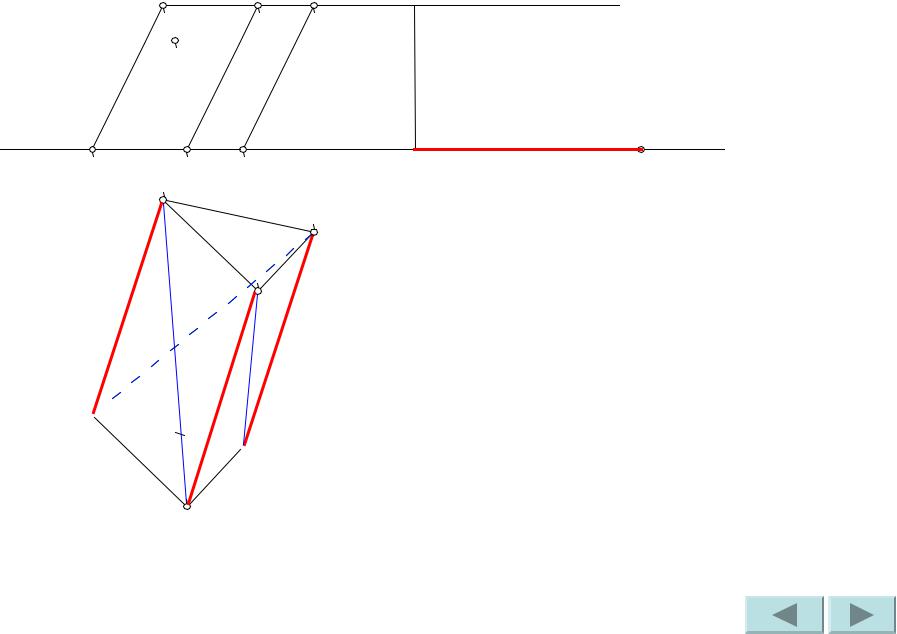
Найдем
натуральную величину ребер. Построим 2-ой катет, равный горизонтальным проекциям этих ребер.
A1



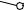
 C1
C1
B1
A' |
B' |
C' |
2 |
2 |
2 |
|
2 |
|
|
M |
|
П2 |
A |
|
B |
C |
|
A' |
|||
П1 2 |
1 |
2 |
2 |
|
|
|
|
C' |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
B'1 |
|
|
|
|
|
|
|
|
|
|
A1



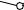
 C1
C1
B1
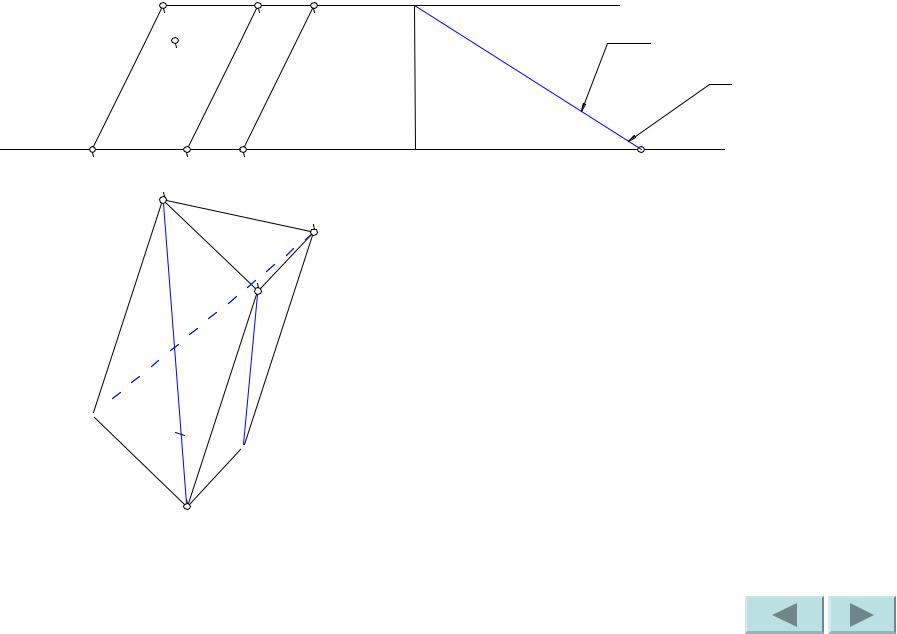
Н.В.
ребро
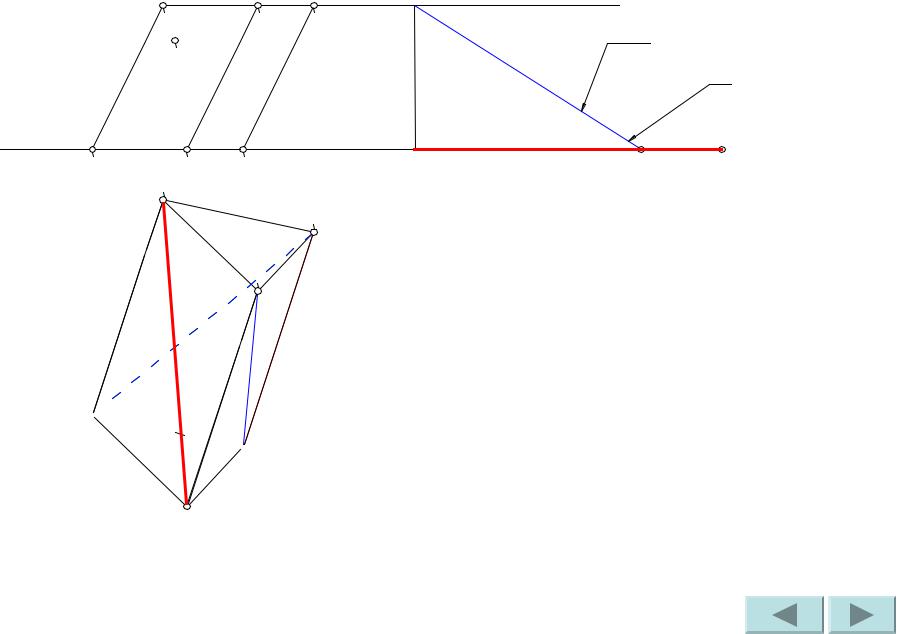
Гипотенуза – искомая натуральная величина ребер.
A' |
B' |
C' |
2 |
2 |
2 |
|
2 |
|
|
M |
|
П2 |
A |
|
B |
C |
|
A' |
|||
П1 2 |
1 |
2 |
2 |
|
|
|
|
C' |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
B'1 |
|
|
|
|
|
|
|
|
|
|
A1



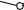
 C1
C1
B1
Н.В.
ребро
Аналогично найдем натуральную величину диагонали A’B.
A' |
B' |
C' |
2 |
2 |
2 |
|
2 |
|
|
M |
|
П2 |
A |
|
B |
C |
|
A' |
|||
П1 2 |
1 |
2 |
2 |
|
|
|
|
C' |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
B'1 |
|
|
|
|
|
|
|
|
|
|
A1



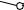
 C1
C1
B1
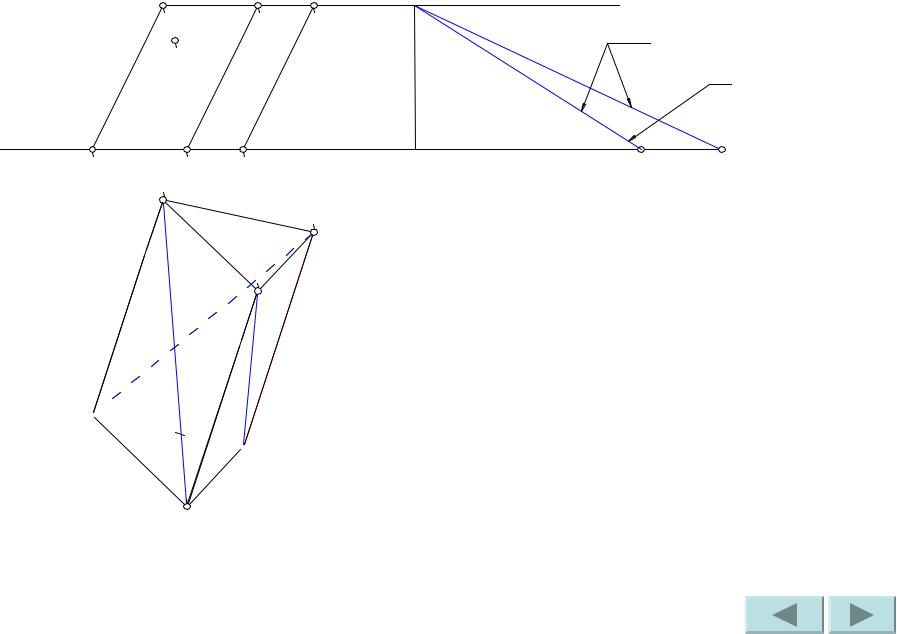
Н.В.
ребро
Гипотенуза – искомая натуральная величина диагонали A’B..
|
|
A' |
|
B' |
C' |
|
|
|
|
2 |
M |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
Н.В. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ребро |
П2 |
A |
|
B |
C |
|
|
|
П1 2 |
A' |
2 |
2 |
|
|
||
|
|
1 |
|
|
|
|
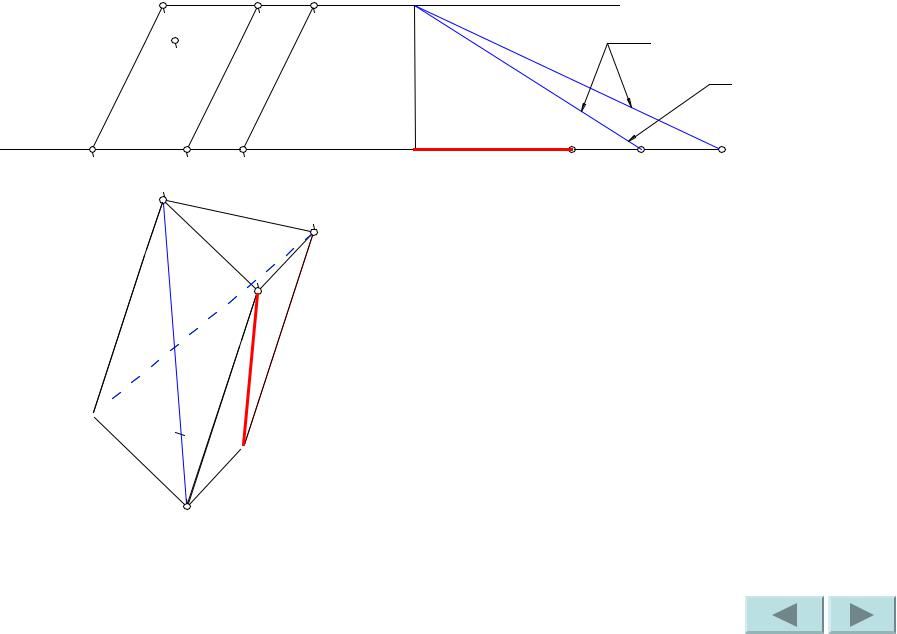
Аналогично найдем |
|
|
|
|
|
C' |
|
|
|
|
|
|
|
|
натуральную |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
величину диагонали |
|
|
|
|
1 |
|
|
B’C. |
|
|
|
|
B' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1



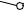
 C1
C1
B1
|
|
A' |
|
B' |
C' |
|
|
|
|
2 |
M |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
Н.В. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ребро |
П2 |
A |
|
B |
C |
|
|
|
П1 2 |
A' |
2 |
2 |
|
|
||
|
|
1 |
|
|
|
|
Гипотенуза – |
|
|
|
|
|
C' |
|
|
|
|
|
|
|
|
искомая |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
натуральная |
|
|
|
|
1 |
|
|
величина диагонали |
|
|
|
|
B' |
|
|
B’C. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
A1



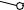
 C1
C1
B1
|
|
A' |
|
B' |
C' |
|
|
|
|
|
2 |
M |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
Н.В. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ребро |
П2 |
|
|
|
|
|
|
|
|
П1 |
2 |
|
2 |
2 |
|
|
|
|
|
A |
A' |
B |
C |
|
|
||
|
|
1 |
|
|
|
|
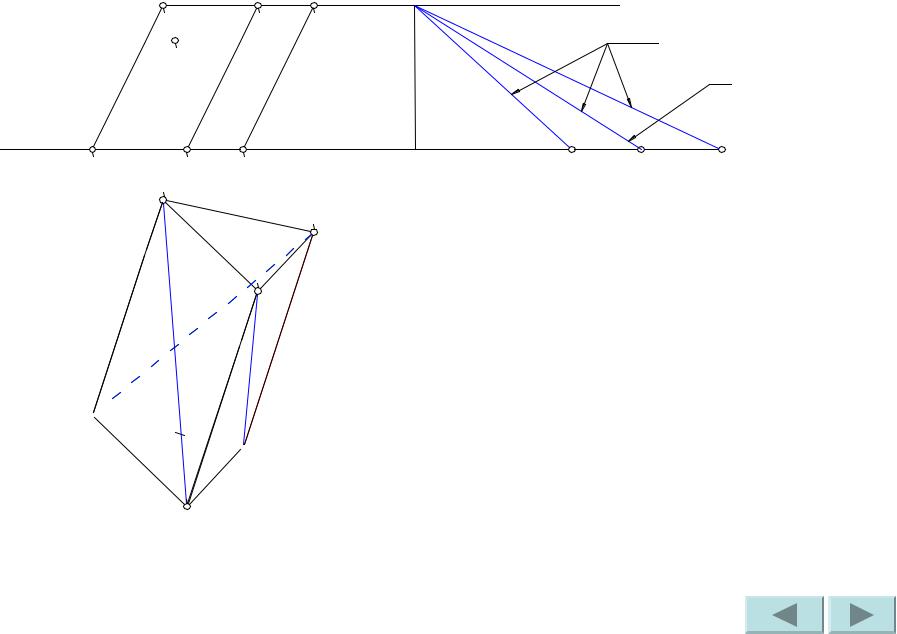
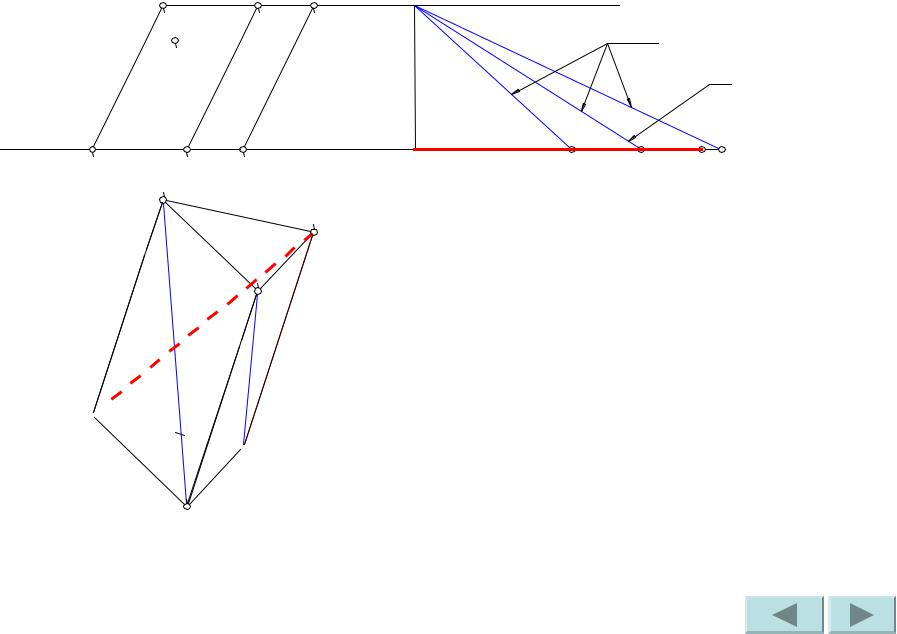
Аналогично найдем |
|
|
|
|
|
|
C' |
|
||
|
|
|
|
|
|
натуральную |
||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
величину диагонали |
|
|
|
|
|
1 |
|
|
C’A. |
|
|
|
|
|
B' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1



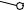
 C1
C1
B1
|
|
2 |
|
B' |
C' |
|
|
|
|
|
A' |
|
2 |
2 |
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
Н.В. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ребро |
П2 |
|
|
|
|
|
|
|
|
П1 |
2 |
|
2 |
2 |
|
|
|
|
|
A |
A' |
B |
C |
|
|
||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
C' |
|
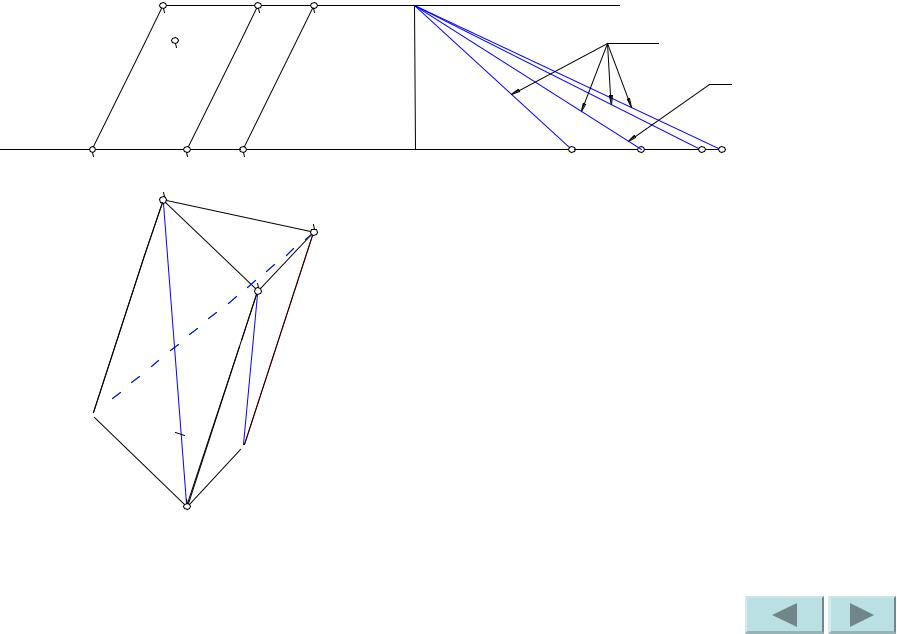
Гипотенуза – |
|
|
|
|
|
|
|
искомая |
||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
натуральная |
|
|
|
|
|
1 |
|
|
величина диагонали |
|
|
|
|
|
B' |
|
|
C’A. |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
A1



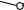
 C1
C1
B1
2 |
B' |
C' |
A' |
2 |
2 |
M |
|
|
2 |
|
|
П2 |
A |
|
B |
C |
П1 |
A' |
|||
2 |
1 |
2 |
2 |
|
|
|
|
|
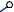
 C'1
C'1
|
|
|
|
B'1 |
|
|
||
|
A1



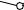
 C1
C1
B1
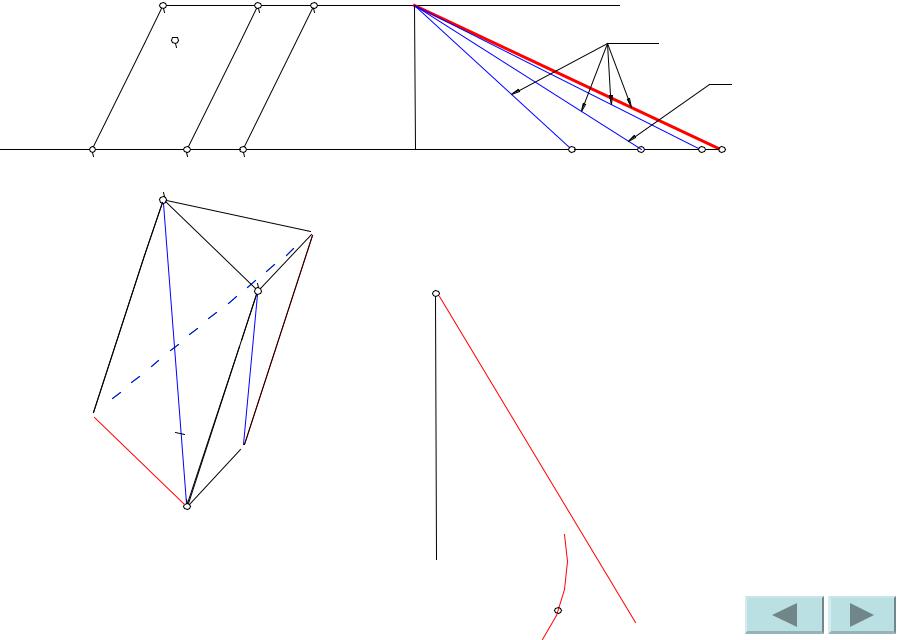
Построим первый элемент развертки – натуральную величину ребра AA’.
Н.В.
ребро
|
|
|
A'
A
2 |
B' |
C' |
A' |
2 |
2 |
M |
|
|
2 |
|
|
П2 |
A |
|
B |
C |
П1 |
A' |
|||
2 |
1 |
2 |
2 |
|
|
|
|
|
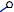
 C'1
C'1
|
|
|
|
B'1 |
|
|
||
|
A1



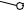
 C1
C1
B1
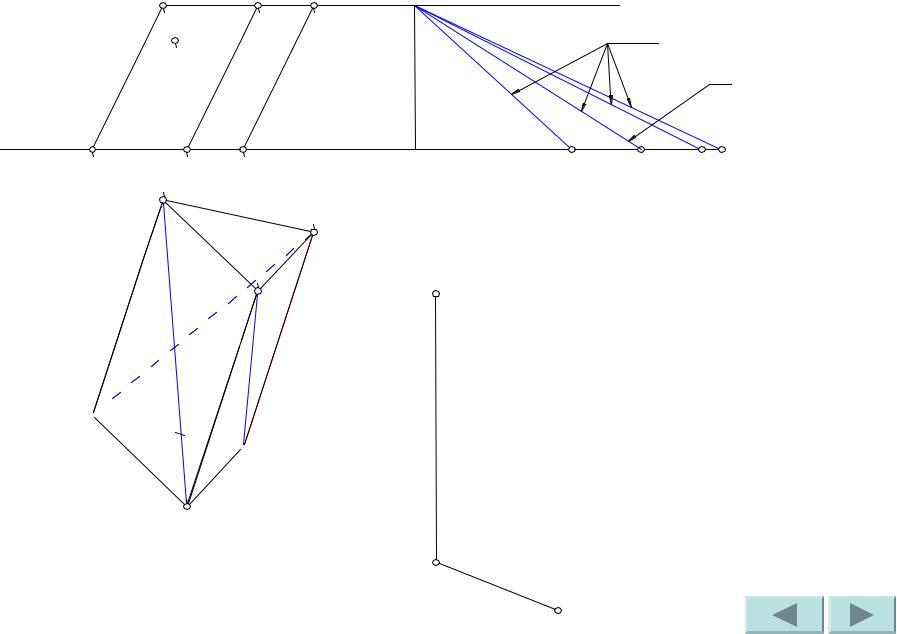
Сделаем засечки радиусами A1B1 и A’B из точек A и A’ соответственно. Точка пересечения засечек – искомая точка B.
Н.В.
ребро
|
|
|
A'
A

2 |
B' |
C' |
A' |
2 |
2 |
M |
|
|
2 |
|
Н.В. |
|
|
ребро
П2 |
|
|
|
|
|
|
|
П1 |
2 |
|
2 |
2 |
|
|
|
|
A |
A' |
B |
C |
|
||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
C' |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
A' |
|
|
|
|
|
|
B'1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1



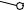
 C1
C1
B1
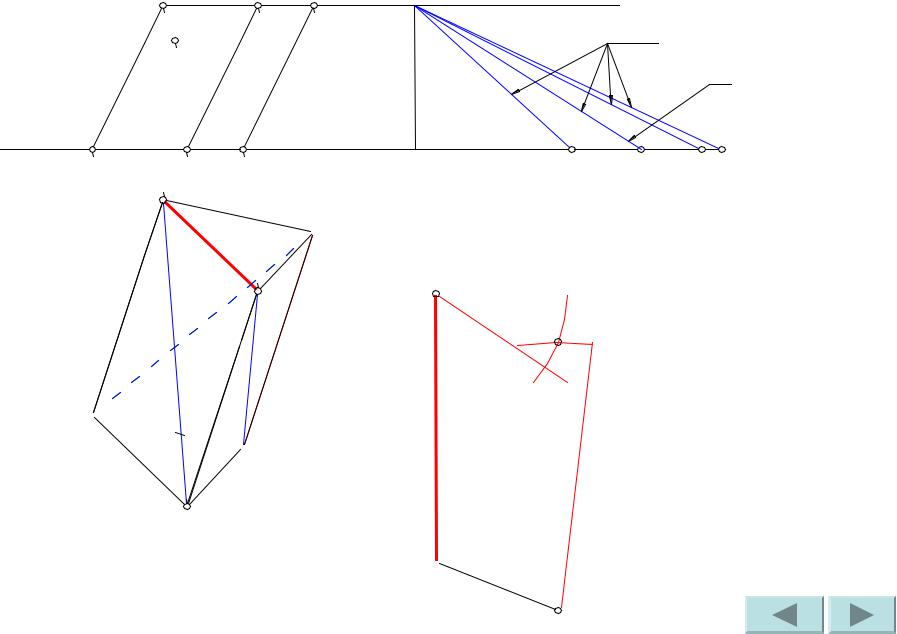
Проводим ребро AB.
A
B
2 |
B' |
C' |
A' |
2 |
2 |
M |
|
|
2 |
|
|
П2 |
A |
|
B |
C |
П1 |
A' |
|||
2 |
1 |
2 |
2 |
|
|
|
|
|
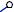
 C'1
C'1
|
|
|
|
B'1 |
|
|
||
|
A1



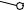
 C1
C1
B1
Сделаем засечки радиусами AA’ и A’1B’1 из точек B и A’ соответственно. Точка пересечения засечек – искомая точка B’.
A'
A
Н.В.
ребро
|
|
|
B
2 |
B' |
C' |
A' |
2 |
2 |
M |
|
|
2 |
|
|
П2 |
A |
|
B |
C |
П1 |
A' |
|||
2 |
1 |
2 |
2 |
|
|
|
|
|
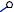
 C'1
C'1
|
|
|
|
B'1 |
|
|
||
|
A1



 C1
C1
B1
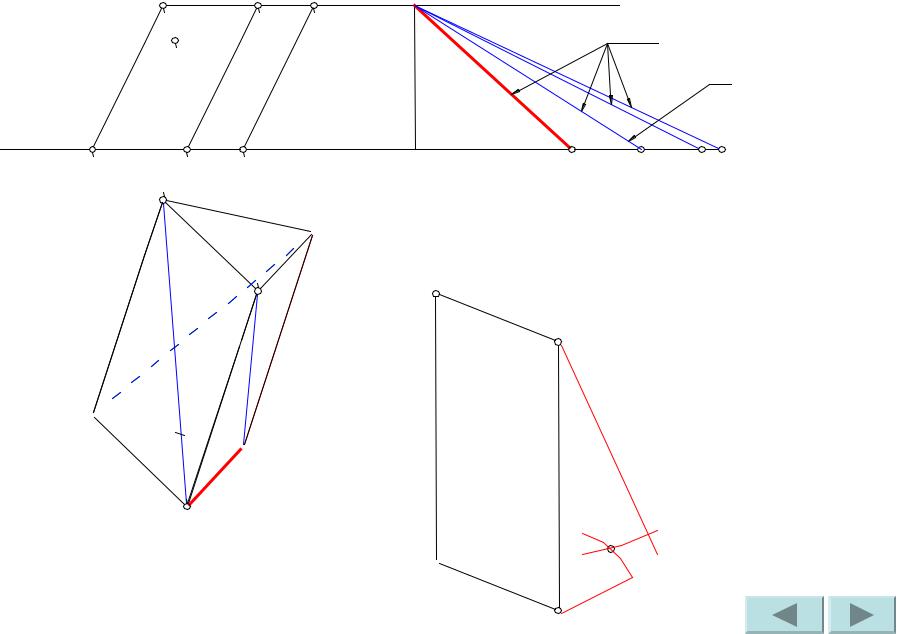
Проводим ребра BB’ и A’B’. 1-ая грань призмы построена.
Н.В.
ребро
|
|
|
A'
B'
A
B
2 |
B' |
C' |
A' |
2 |
2 |
M |
|
|
2 |
|
|
П2 |
A |
|
B |
C |
П1 |
A' |
|||
2 |
1 |
2 |
2 |
|
|
|
|
|
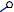
 C'1
C'1
|
|
|
|
B'1 |
|
|
||
|
A1



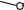
 C1
C1
B1
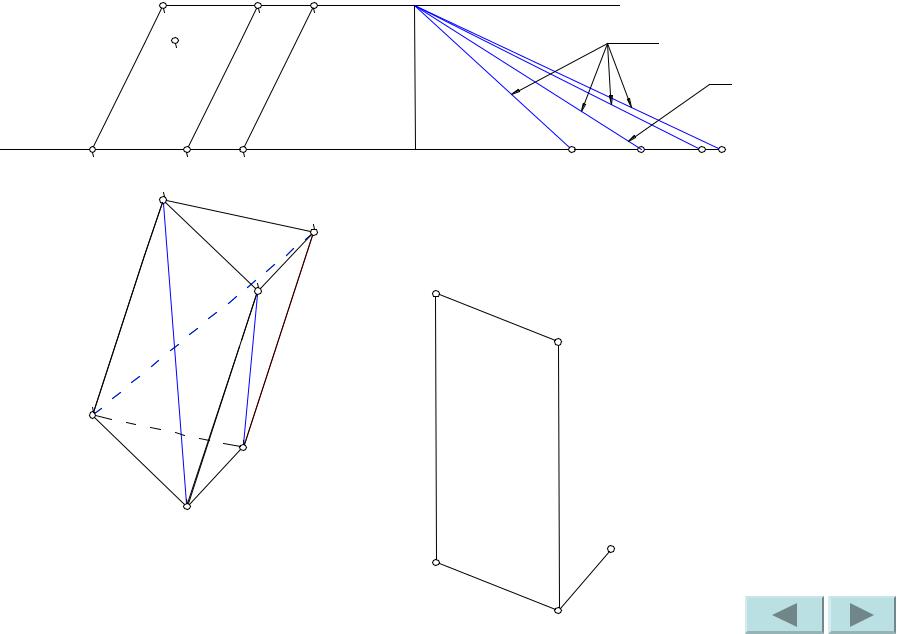
Сделаем засечки радиусами B’C и B1C1 из точек B’ и B соответственно. Точка пересечения засечек – искомая точка C.
Н.В.
ребро
|
|
|
A'
B'
A
B
2 |
B' |
C' |
A' |
2 |
2 |
M |
|
|
2 |
|
Н.В. |
|
|
ребро
П2 |
|
|
|
|
|
|
|
П1 |
2 |
|
2 |
2 |
|
|
|
|
A |
A' |
B |
C |
|
||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
C' |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
A' |
|
|
|
|
|
|
B'1 |
|
|
|
|
|
|
|
B' |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
A |
|
|
1 |
C |
|
|
1 |
|
B1 |
|
|
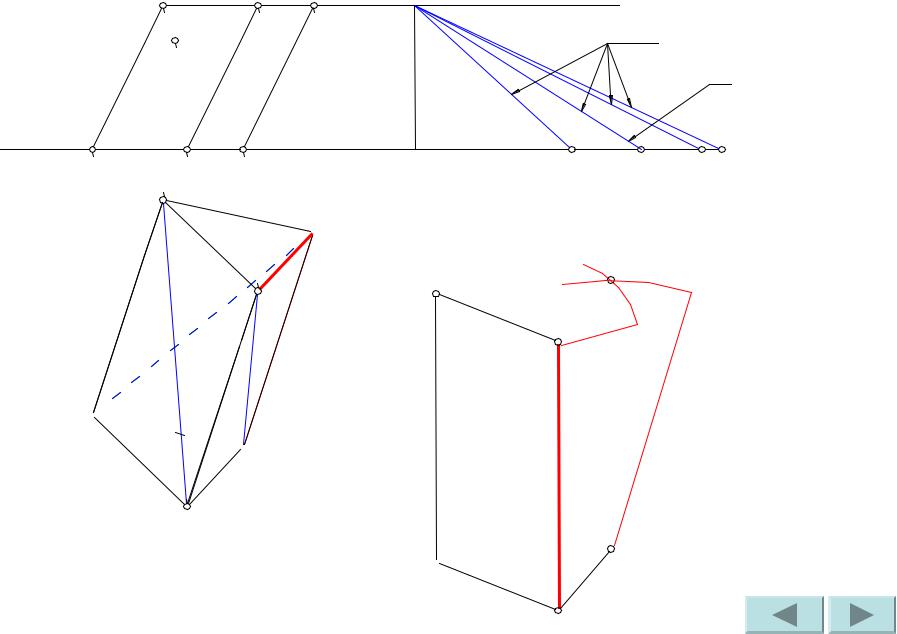
Проводим ребро BC. |
A |
C |
|
B
2 |
B' |
C' |
A' |
2 |
2 |
M |
|
|
2 |
|
|
П2 |
A |
|
B |
C |
П1 |
A' |
|||
2 |
1 |
2 |
2 |
|
|
|
|
|
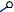
 C'1
C'1
|
|
|
|
B'1 |
|
|
||
|
A1



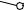
 C1
C1
B1
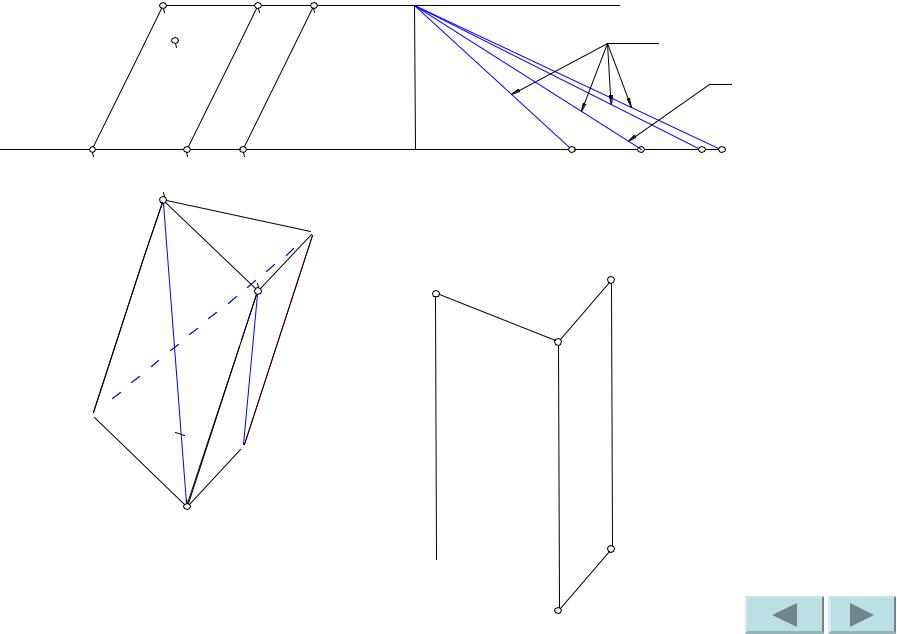
Сделаем засечки радиусами B’B и B’1C’1 из точек B’ и C соответственно. Точка пересечения засечек – искомая точка C’.
A'
A
Н.В.
ребро
|
|
|
B'
C
B
2 |
B' |
C' |
A' |
2 |
2 |
M |
|
|
2 |
|
|
П2 |
A |
|
B |
C |
П1 |
A' |
|||
2 |
1 |
2 |
2 |
|
|
|
|
|
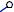
 C'1
C'1
|
|
|
|
B'1 |
|
|
||
|
A1



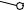
 C1
C1
B1
Проводим ребра CC’ и B’C’. 2-ая грань призмы построена.
Н.В.
ребро
|
|
|
A' C'
B'
A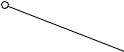 C
C
B
2 |
B' |
C' |
A' |
2 |
2 |
M |
|
|
2 |
|
|
П2 |
A |
|
B |
C |
П1 |
A' |
|||
2 |
1 |
2 |
2 |
|
|
|
|
|
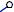
 C'1
C'1
|
|
|
|
B'1 |
|
|
||
|
A1




 C1
C1
B1
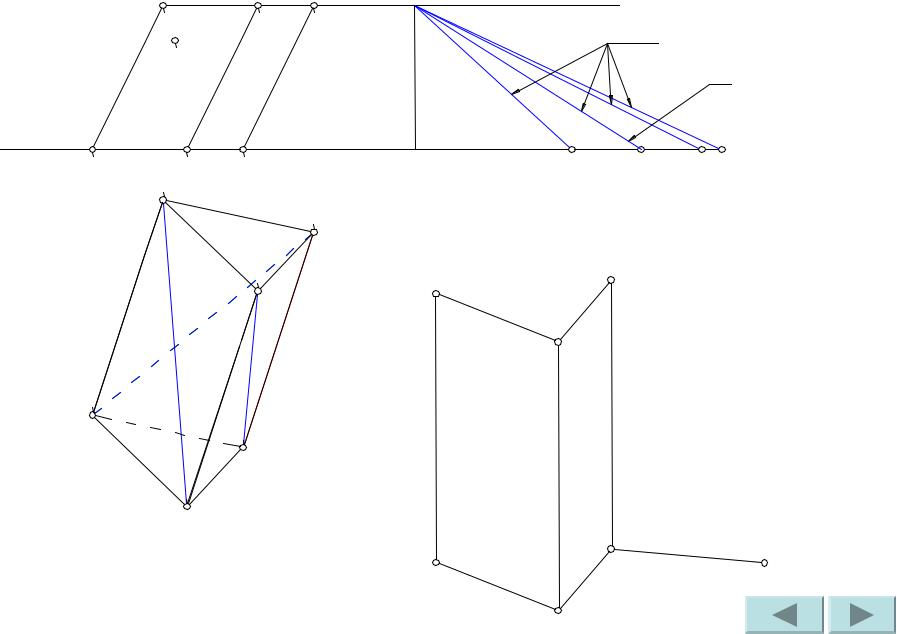
Сделаем засечки радиусами C’A и C1A1 из точек C’ и C соответственно. Точка пересечения засечек – искомая точка A.
Н.В.
ребро
|
|
|
A' C'
B'
A C
C
B
2 |
B' |
C' |
A' |
2 |
2 |
M |
|
|
2 |
|
Н.В. |
|
|
ребро
П2 |
|
|
|
|
|
|
|
|
П1 |
2 |
|
2 |
2 |
|
|
|
|
|
A |
A' |
B |
C |
|
|
||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
C' |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
A' |
|
C' |
|
|
|
|
|
B'1 |
|
|
|
|
|
|
|
|
|
B' |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
A |
|
|
|
1 |
C |
|
|
|
1 |
|
|
B1 |
|
|
|
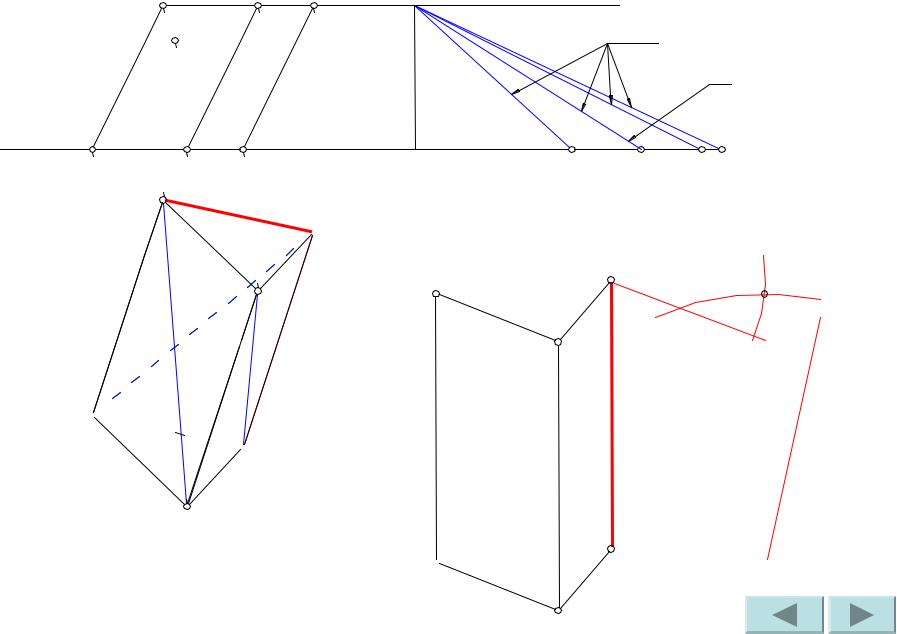
Проводим ребро CA. |
A |
C |
A |
|
B
2 |
B' |
C' |
A' |
2 |
2 |
M |
|
|
2 |
|
|
П2 |
A |
|
B |
C |
П1 |
A' |
|||
2 |
1 |
2 |
2 |
|
|
|
|
|
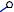
 C'1
C'1
|
|
|
|
B'1 |
|
|
||
|
A1



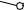
 C1
C1
B1
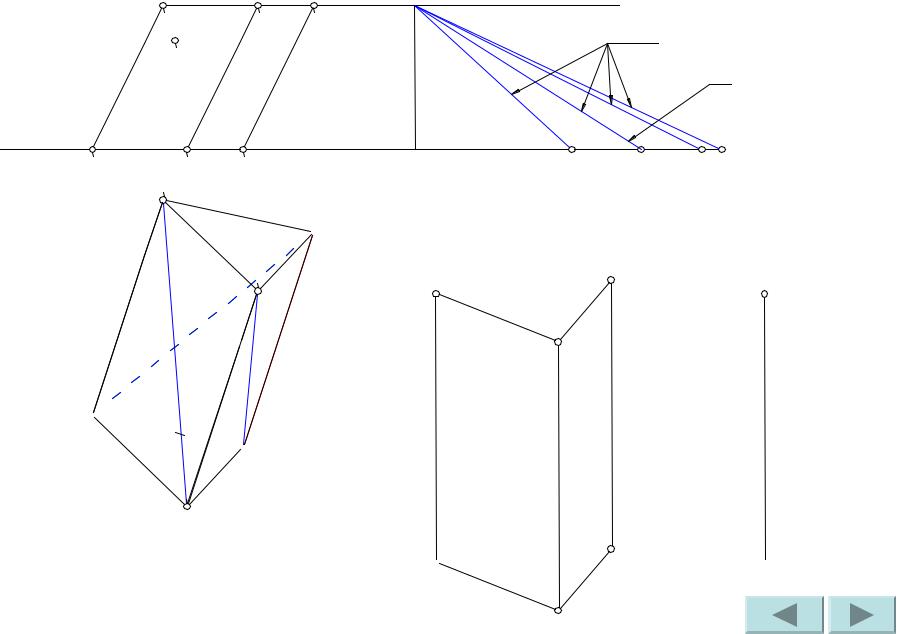
Сделаем засечки радиусами C’C и C’1A’1 из точек A и C’ соответственно. Точка пересечения засечек – искомая точка A’.
A'
A
Н.В.
ребро
|
|
|
C'
B'
C A
A
B
2 |
B' |
C' |
A' |
2 |
2 |
M |
|
|
2 |
|
|
П2 |
A |
|
B |
C |
П1 |
A' |
|||
2 |
1 |
2 |
2 |
|
|
|
|
|
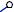
 C'1
C'1
|
|
|
|
B'1 |
|
|
||
|
A1



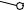
 C1
C1
B1
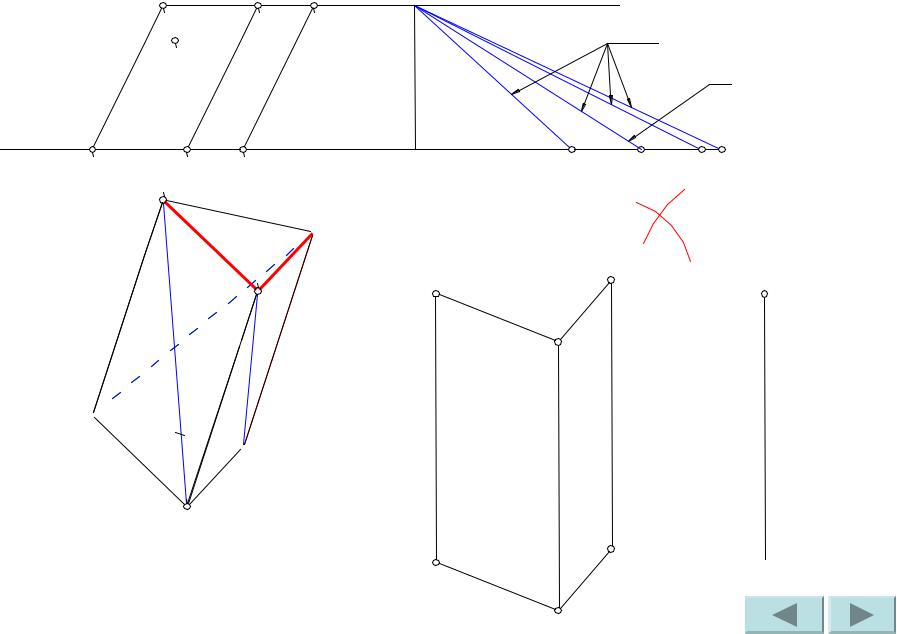
Проводим ребра AA’ и C’A’. 3-я грань призмы построена.
A'
A
Н.В.
ребро
|
|
|
C' A'
A'
B'
C A
A
B
2 |
B' |
C' |
A' |
2 |
2 |
M |
|
|
2 |
|
|
П2 |
A |
|
B |
C |
П1 |
A' |
|||
2 |
1 |
2 |
2 |
|
|
|
|
|
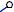
 C'1
C'1
|
|
|
|
B'1 |
|
|
||
|
A1



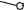
 C1
C1
B1
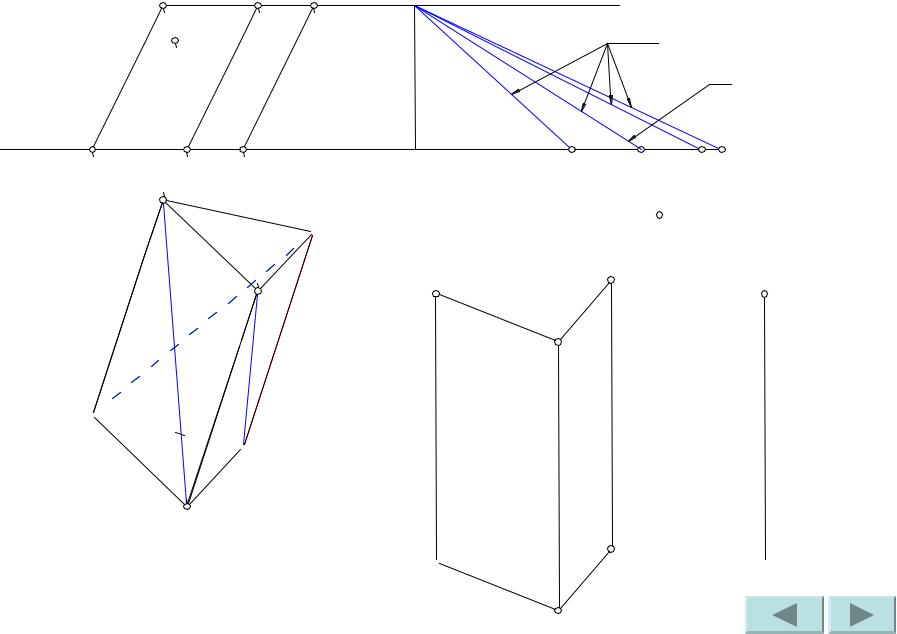
Сделаем засечки радиусами A’1B’1 и C’1B’1 из точек A’ и C’ соответственно. Точка пересечения засечек – искомая точка B’.
Н.В.
ребро
|
|
|
A' C' A'
A'
B'
A C A B
A B 
2 |
B' |
C' |
A' |
2 |
2 |
M |
|
|
2 |
|
|
П2 |
A |
|
B |
C |
П1 |
A' |
|||
2 |
1 |
2 |
2 |
|
|
|
|
|
 C'1
C'1
|
|
|
|
B'1 |
|
|
||
|
A1



 C1
C1
B1
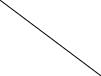
Проводим ребра A’B’ и C’B’. 4-я грань призмы построена.
A'
A
Н.В.
ребро
|
|
|
B'
C'
 A'
A'
B'
C A
A
B
2 |
B' |
C' |
A' |
2 |
2 |
M |
|
|
2 |
|
|
П2 |
A |
|
B |
C |
П1 |
A' |
|||
2 |
1 |
2 |
2 |
|
|
|
|
|
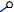
 C'1
C'1
|
|
|
|
B'1 |
|
|
||
|
A1



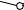
 C1
C1
B1
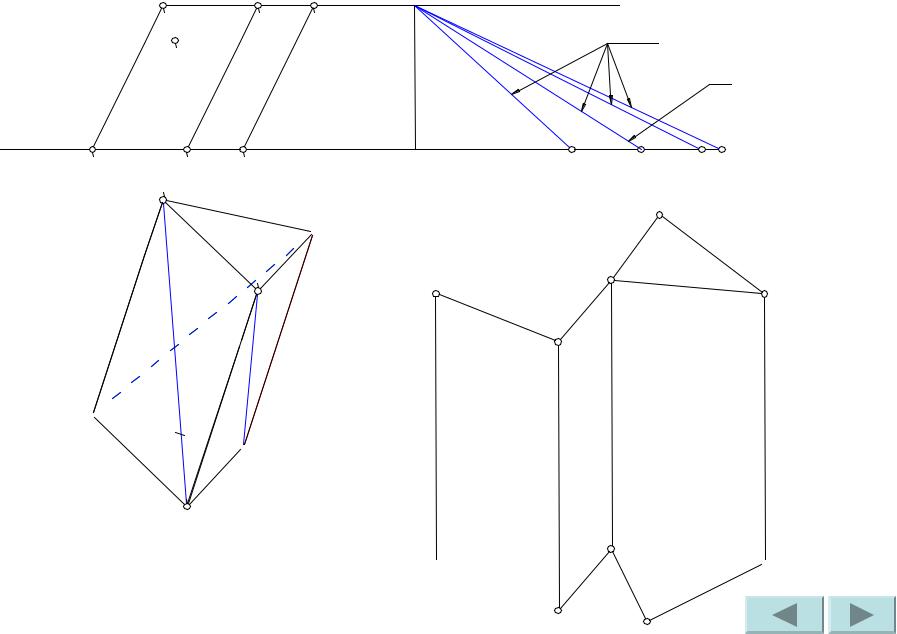
Сделаем засечки радиусами A’B’ и C’B’из точек A и C соответственно. Точка пересечения засечек – искомая точка B.
Н.В.
ребро
|
|
|
|
B' |
|
A' |
C' |
A' |
|
||
B' |
|
|
A C A B
A B 

2 |
B' |
C' |
A' |
2 |
2 |
M |
|
|
2 |
|
|
П2 |
A |
|
B |
C |
П1 |
A' |
|||
2 |
1 |
2 |
2 |
|
|
|
|
|
 C'1
C'1
|
|
|
|
B'1 |
|
|
||
|
A1



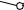
 C1
C1
B1
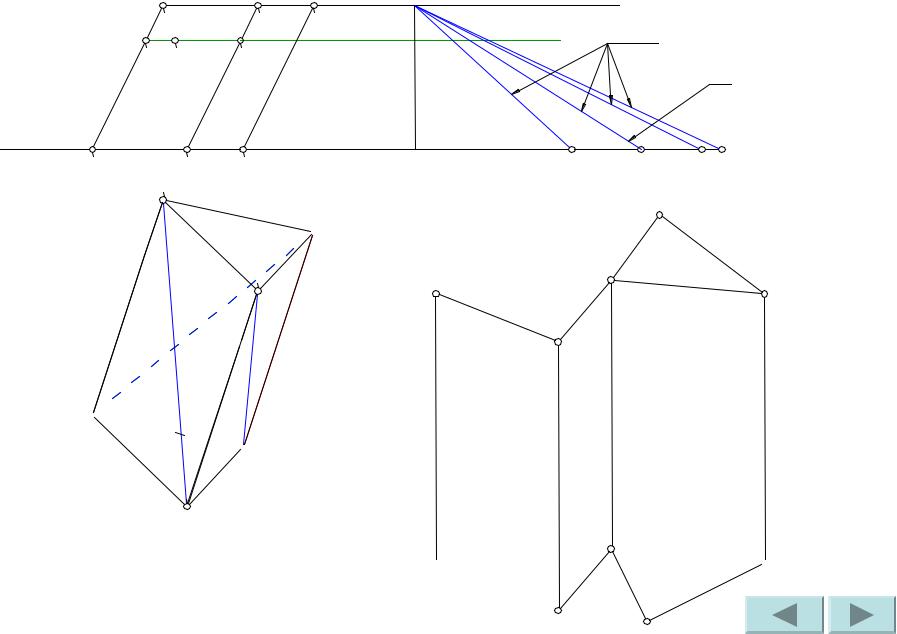
Проводим ребра AB и CB. Развертка призмы построена.
Н.В.
ребро
|
|
|
|
B' |
|
A' |
C' |
A' |
|
||
B' |
|
|
A C
C A
A
B B
2 |
B' |
C' |
A' |
2 |
2 |
M |
|
|
2 |
|
|
П2 |
A |
|
B |
C |
П1 |
A' |
|||
2 |
1 |
2 |
2 |
|
|
|
|
|
 C'1
C'1
|
|
|
|
B'1 |
|
|
||
|
A1



 C1
C1
B1
Проводим горизонталь через фронтальную проекцию точки M.
Н.В.
ребро
|
|
|
|
B' |
|
A' |
C' |
A' |
|
||
B' |
|
|
A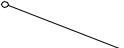 C
C A
A
B B
2 |
B' |
C' |
A' |
2 |
2 |
M |
|
|
2 |
|
|
П2 |
A |
|
B |
C |
П1 |
A' |
|||
2 |
1 |
2 |
2 |
|
|
|
|
|
 C'1
C'1
|
|
|
|
B'1 |
|
|
||
|
A1



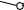
 C1
C1
B1
Находим, в каком отношении эта горизонталь делит натуральную величину ребер.
 M Н.В.
M Н.В.
ребро
|
|
|
|
B' |
|
A' |
C' |
A' |
|
||
B' |
|
|
A C
C A
A
B B
2 |
B' |
C' |
A' |
2 |
2 |
M |
|
|
2 |
|
|
П2 |
A |
|
B |
C |
П1 |
A' |
|||
2 |
1 |
2 |
2 |
|
|
|
|
|
 C'1
C'1
|
|
|
|
B'1 |
|
|
||
|
A1



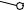
 C1
C1
B1
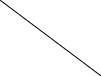
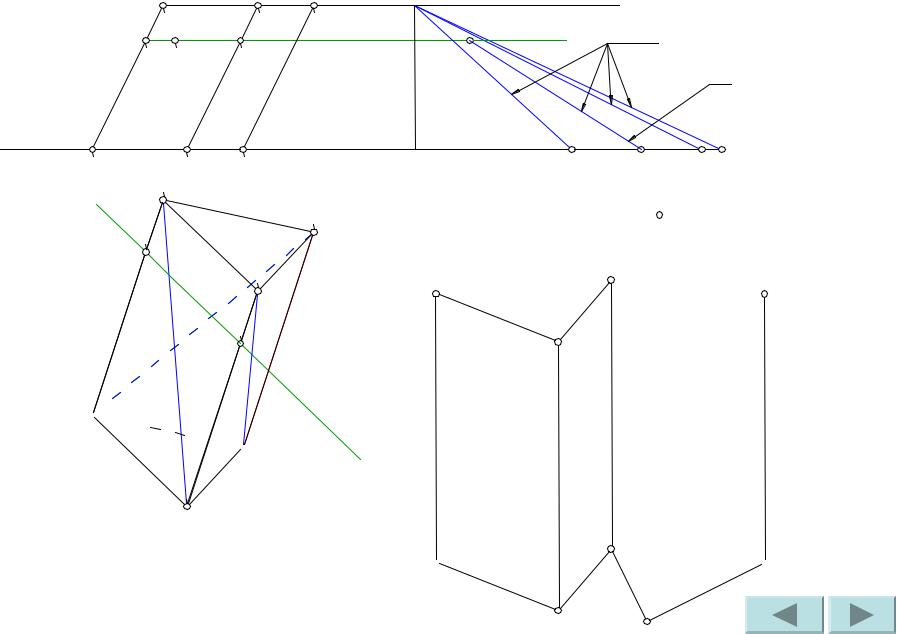
Находим по принадлежности горизонтальные проекции точек пересечения горизонтали с ребрами призмы.
 M
M
A'
A
Н.В.
ребро
|
|
|
B'
C'
 A'
A'
B'
C A
A
B B
A' |
B' |
C' |
2 |
2 |
2 |
|
2 |
|
|
M |
|
П2 |
A |
|
B |
C |
|
A' |
|||
П1 2 |
1 |
2 |
2 |
|
|
|
|
C' |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
B'1 |
|
|
|
|
|
|
|
|
|
|
A1


 C1
C1
B1
Проводим проекцию горизонтали в плоскости П1
 M
M
A'
A
Н.В.
ребро
|
|
|
B'
C'
 A'
A'
B'
C A
A
B B
A' |
B' |
C' |
2 |
2 |
2 |
|
2 |
|
|
M |
|
П2 П1 A2
A1

A'1 B2 C2
 C'1
C'1
M1 |
|
|
|
B'1 |
|
|
||
|

 C1
C1
B1
Находим по принадлежности горизонтальную проекцию точки M.
 M
M
A'
A
Н.В.
ребро
|
|
|
B'
C'
 A'
A'
B'
C A
A
B B
A' |
B' |
C' |
2 |
2 |
2 |
|
2 |
|
|
M |
|
П2 П1 A2
A1

A'1 B2 C2
 C'1
C'1
M1 |
|
|
|
B'1 |
|
|
||
|

 C1
C1
B1
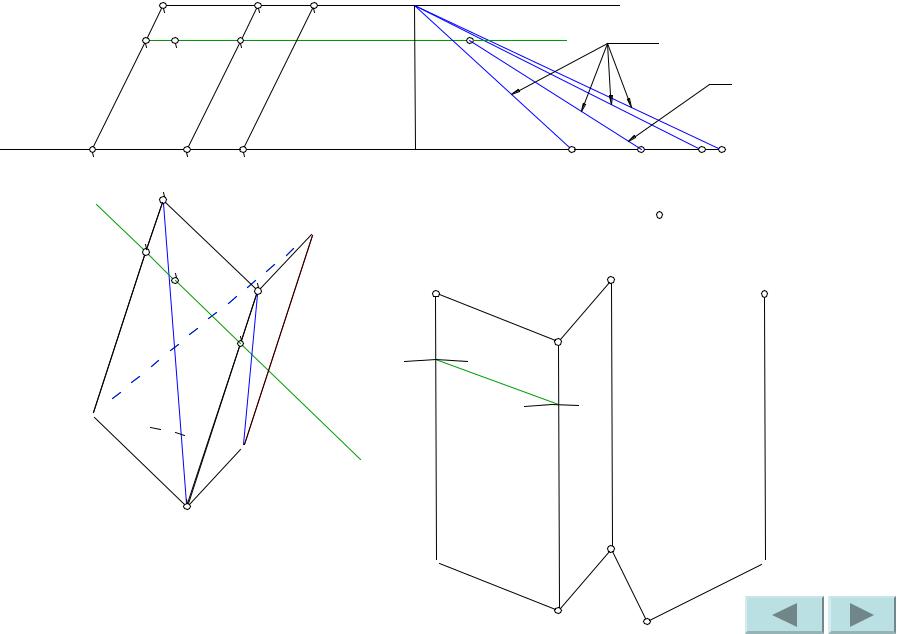
Сделаем засечки, радиусы которых равны большему из отрезков, на которые горизонталь делит натуральные величины ребер. Засечки делаем из точек A и B.
 M
M
A'
A
Н.В.
ребро
|
|
|
B'
C'
 A'
A'
B'
C A
A
B B
A' |
B' |
C' |
2 |
2 |
2 |
|
2 |
|
|
M |
|
П2 П1 A2
A1

A'1 B2 C2
 C'1
C'1
M1 |
|
|
|
B'1 |
|
|
||
|

 C1
C1
B1
Проводим отрезок горизонтали на развертке.
 M
M
A'
A
Н.В.
ребро
|
|
|
B'
C'
 A'
A'
B'
C A
A
B B
A' |
B' |
C' |
2 |
2 |
2 |
|
2 |
|
|
M |
|
П2 П1 A2
A1

A'1 B2 C2
 C'1
C'1
M1 |
|
|
|
B'1 |
|
|
||
|

 C1
C1
B1
Сделаем засечку радиусом, равным отрезку горизонтали между точкой M1 и ребром B1B’1.
 M
M
A'
A
Н.В.
ребро
|
|
|
B'
C'
 A'
A'
B'
C A
A
B B
A' |
B' |
C' |
2 |
2 |
2 |
|
2 |
|
|
M |
|
П2 |
A |
|
B |
C |
|
A' |
|||
П1 2 |
1 |
2 |
2 |
|
|
|
|
C' |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
M1 |
|
|
|
|
|
B'1 |
|
|
|
|
|
|
|
|
|
|
A1



 C1
C1
B1
Строим точку M на развертке.
 M
M
A'
 M
M
A
Н.В.
ребро
|
|
|
B'
C'
 A'
A'
B'
C A
A
B B
|
|
A' |
|
B' |
C' |
|
|
|
|
|
|
2 |
|
2 |
2 |
|
|
|
|
|
|
|
2 |
|
|
M |
|
|
|
|
|
|
M |
|
|
|
|
Н.В. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ребро |
П2 |
|
|
|
|
|
|
|
|
|
П1 |
2 |
|
2 |
2 |
|
|
|
|
|
|
A |
A' |
B |
C |
|
|
|
||
|
|
|
|
|
|
|
B' |
|
|
|
|
1 |
|
|
C' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
A' |
|
|
C' |
A' |
|
|
|
M |
B'1 |
|
B' |
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
M |
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
C |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
B1 |
|
|
|
|
|
|
|
Задача решена. |
|
|
A |
|
|
C |
A |
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
B |
B |
|
|
|
|
|
|
|
|
|
|
|
