начерт_зачет_уч.год_2020_2021 / Билет 4

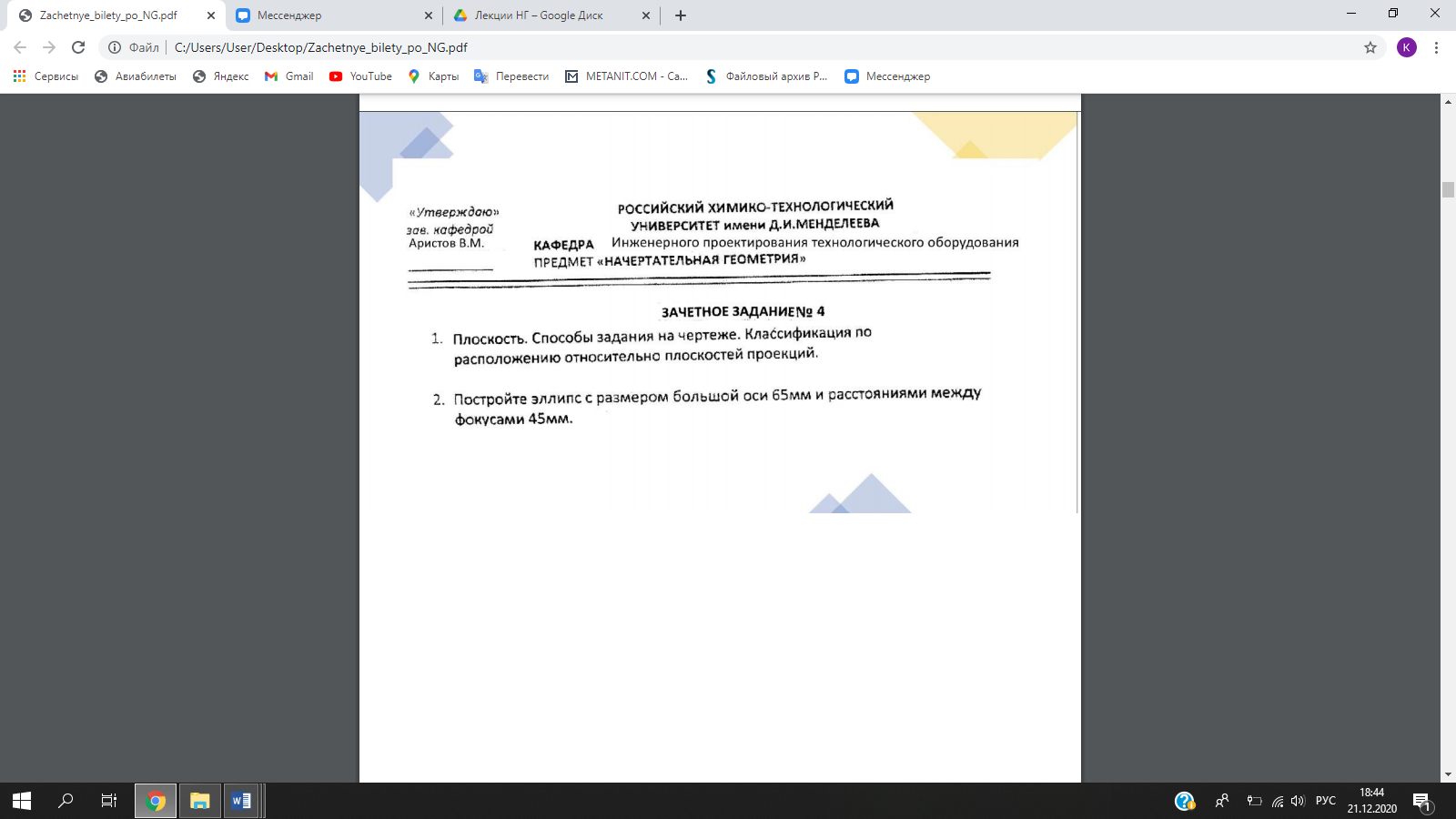
Плоскость можно рассматривать как результат перемещения прямолинейной образующей l, все время оставаясь параллельной прямой b, вдоль направляющей а. При этом а является также прямой (рис.3.5). Определитель плоскости записывается следующим образом: (l,а)[lb].

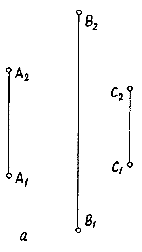
1.Задание плоскости тремя точками. Три точки, не лежащие на одной прямой, задают плоскость (рис.3.6а). Любая четвертая, пятая и т.д. точки, взятые произвольно на чертеже, как правило, не принадлежат заданной плоскости. Определитель: (A, B, C).

 

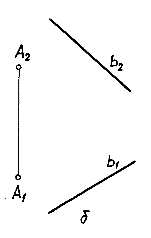
2.Задание плоскости прямой и точкой вне этой прямой. Если две точки плоскости соединить прямой, то получим задание плоскости прямой и точкой

Всякий дополнительный элемент (точка, прямая), взятый произвольно, как правило, не будет принадлежать этой плоскости. Определитель: (A, b)[Ab].

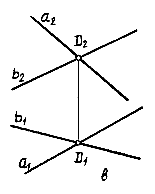
  3.Задание плоскости двумя пересекающимися прямыми. Две пересекающиеся прямые определяют плоскость. Определитель: (а∩b)

 В ряде случаев плоскость удобно задавать двумя пересекающимися прямыми уровня: горизонталью и фронталью.

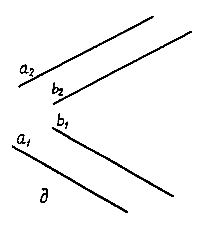
4.Задание плоскости двумя параллельными прямыми. Так как параллельные прямые можно рассматривать как пересекающиеся в несобственной точке, то они также будут определять плоскость. Определитель: (ab)

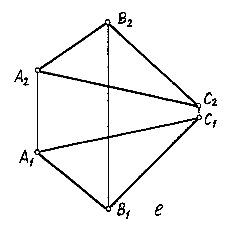
5.Задание плоскости плоской фигурой (отсек плоскости). Любая плоская фигура, например треугольник, задает плоскость. Плоская фигура придает большую наглядность изображаемой плоскости. Определитель: (ABC).

6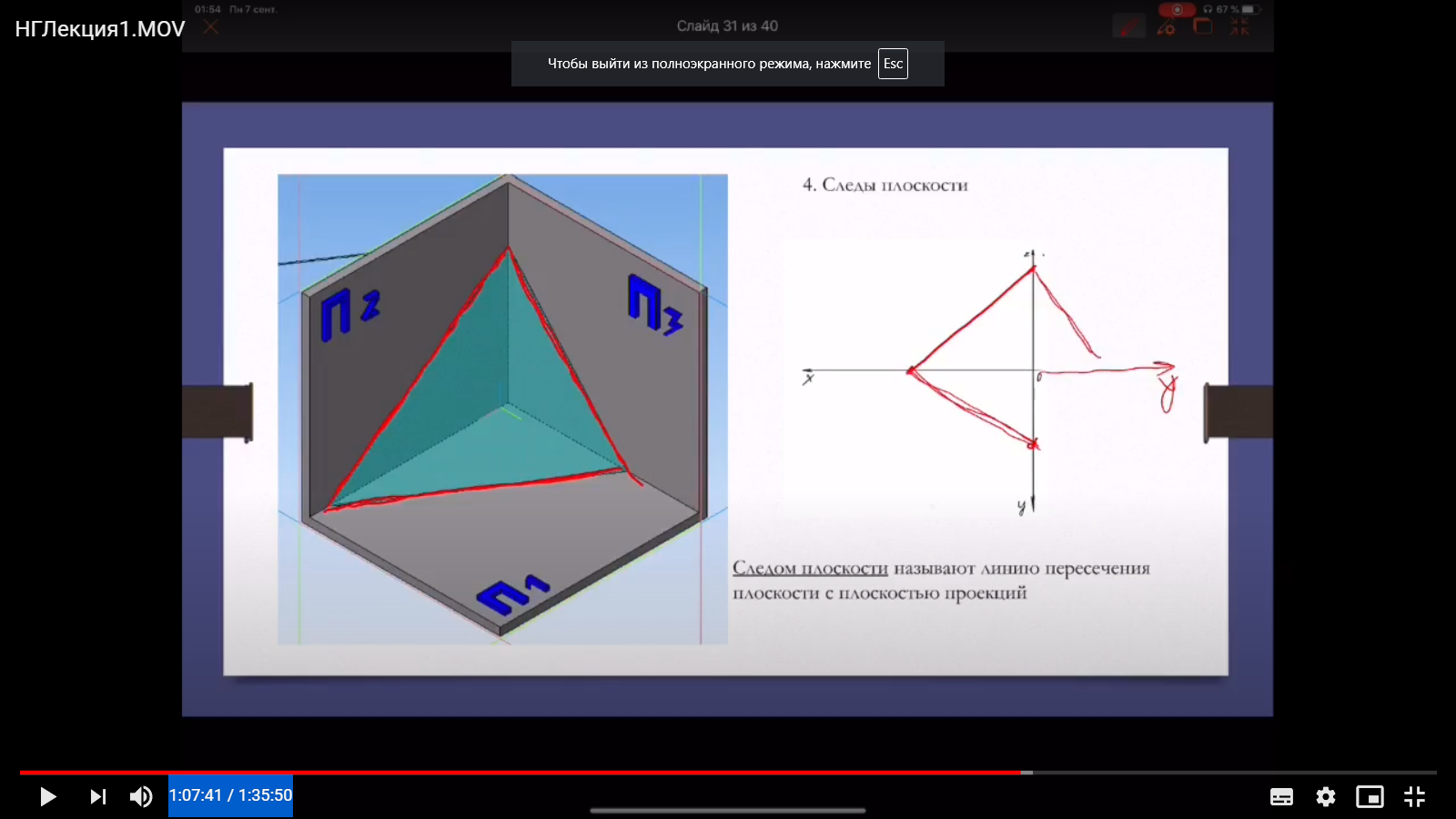 . След плоскости.

Плоскость задается следами плоскости. След плоскости - линия пересечения плоскости с плоскостью проекции. Фронтальный след плоскости, профильный след плоскости, горизонтальный след плоскости. Двух проекций достаточно, чтобы построить проекцию плоскости, т.к. у нас имеется координата y, таким образом мы можем достроить дополнительную проекцию, если это будет необходимо.

При всех случаях задания плоскость считается бесконечной.

Положение плоскости относительно плоскостей проекции:

1 – неперпендикулярно к плоскостям проекции (плоскость общего положения)

2 – перпендикулярно к одной плоскости проекции (плоскость частного положения)

3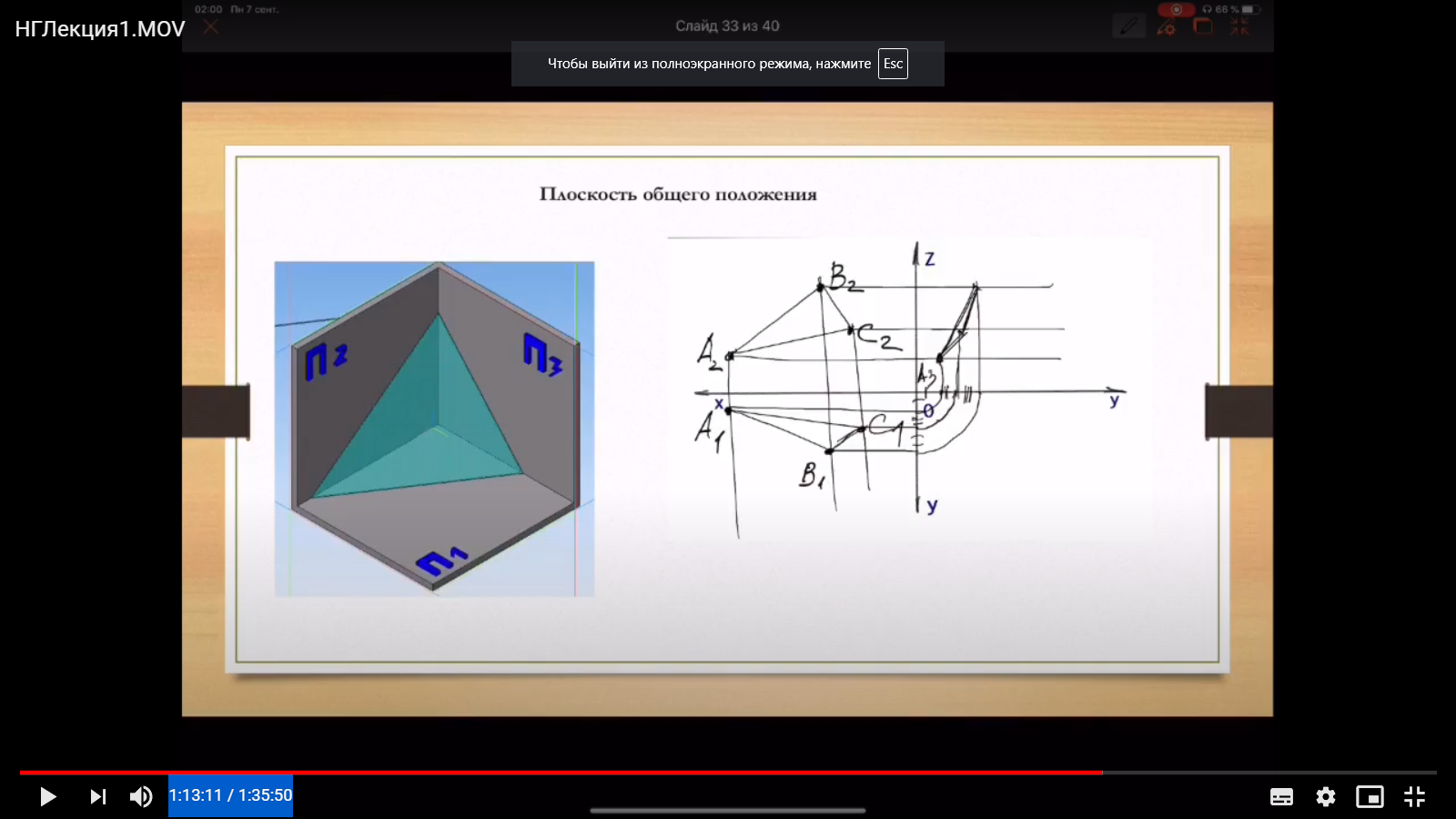 – перпендикулярно двум плоскостям проекции (плоскость частного положения)

Плоскость общего положения.

Плоскость, перпендикулярная одной плоскости проекций.

Т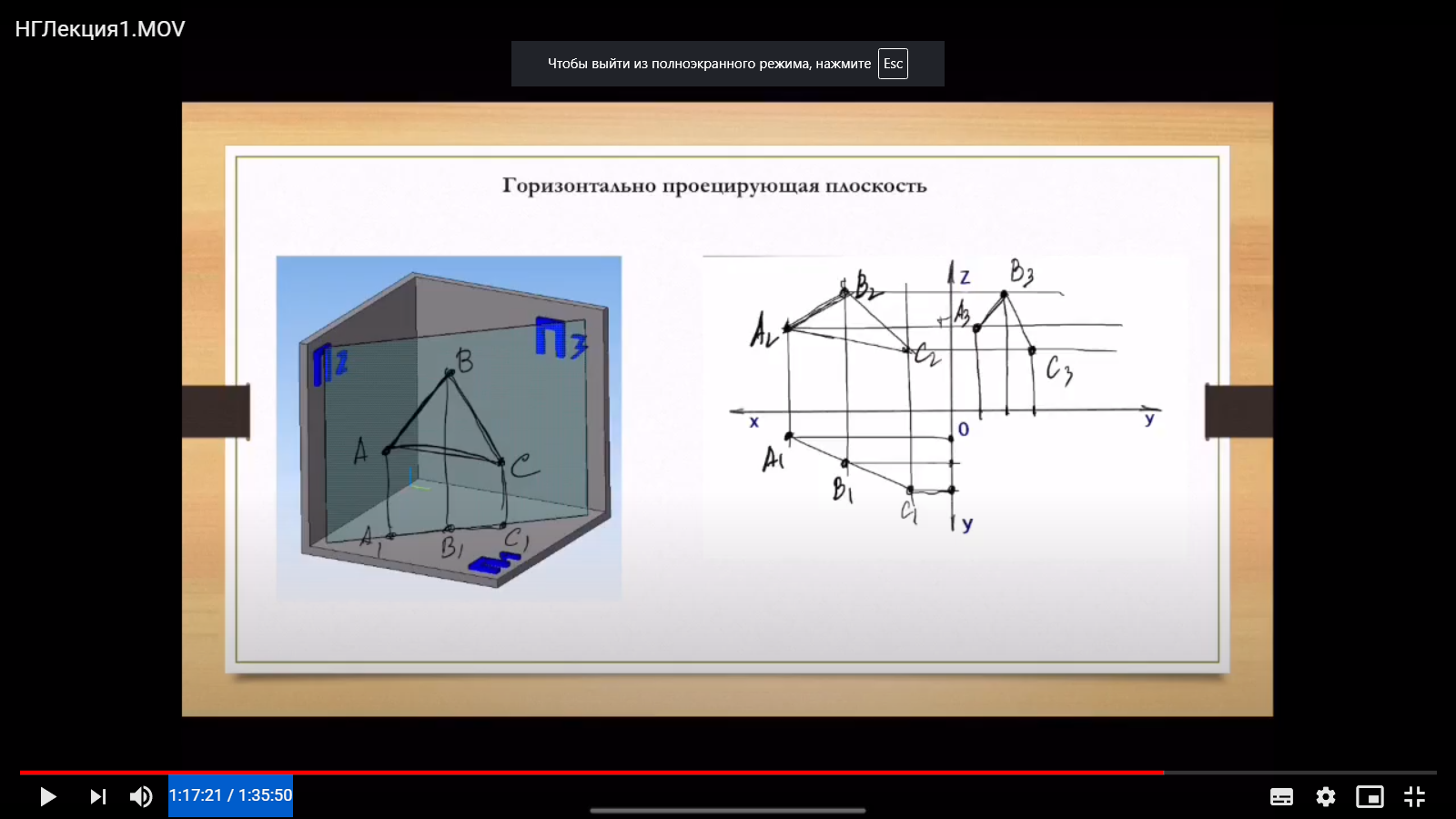 акие плоскости получили название проецирующих плоскостей.

Горизонтально проецирующая плоскость – плоскость, перпендикулярная плоскости П1. Любой элемент этой плоскости проецируется на плоскость П1 в прямую, называемую следом плоскости.

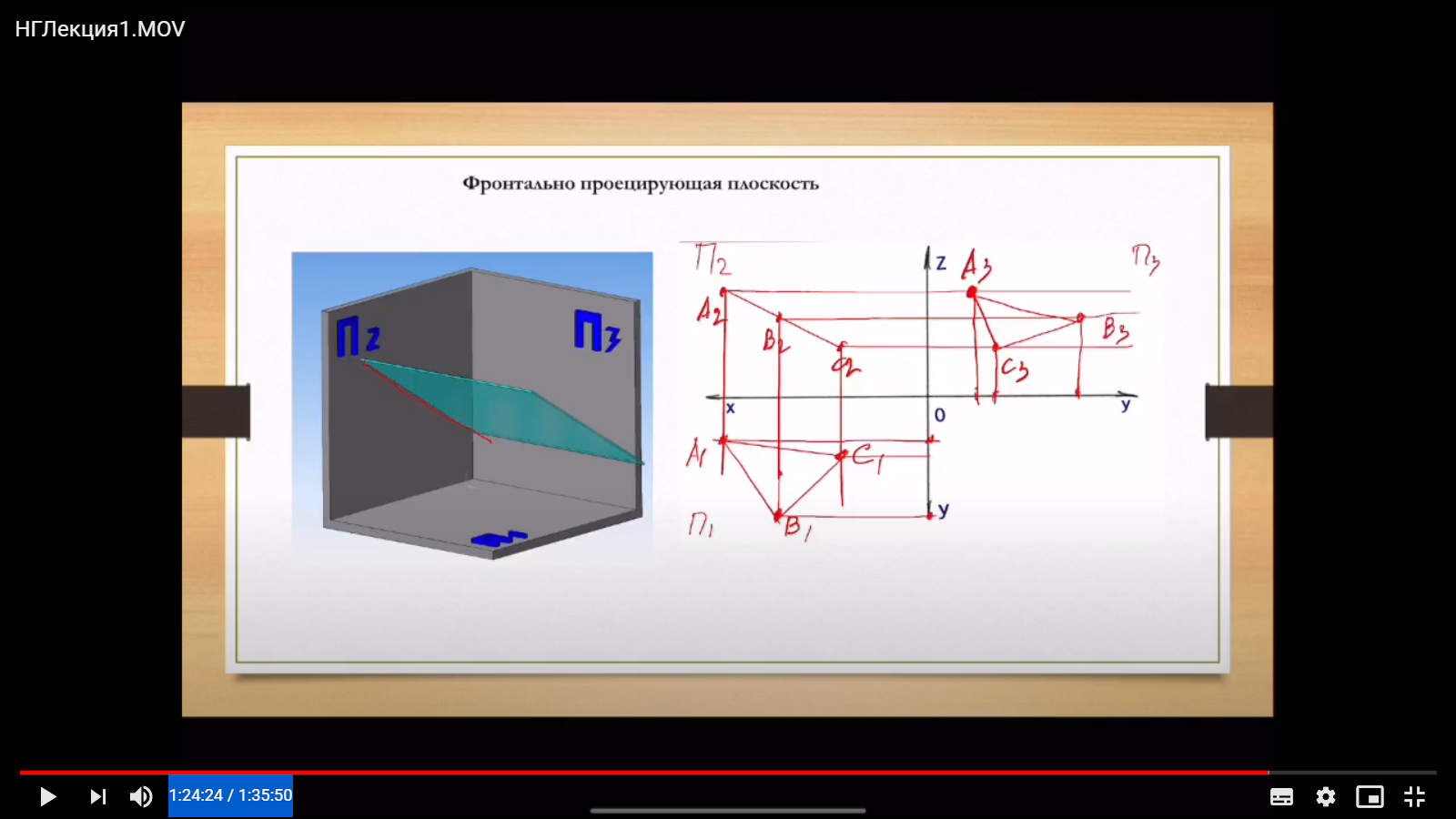
Фронтально проецирующая плоскость – плоскость, перпендикулярная плоскости П2. Любой элемент этой плоскости проецируется на фронтальную плоскость проекций в прямую (фронтальный след плоскости).

П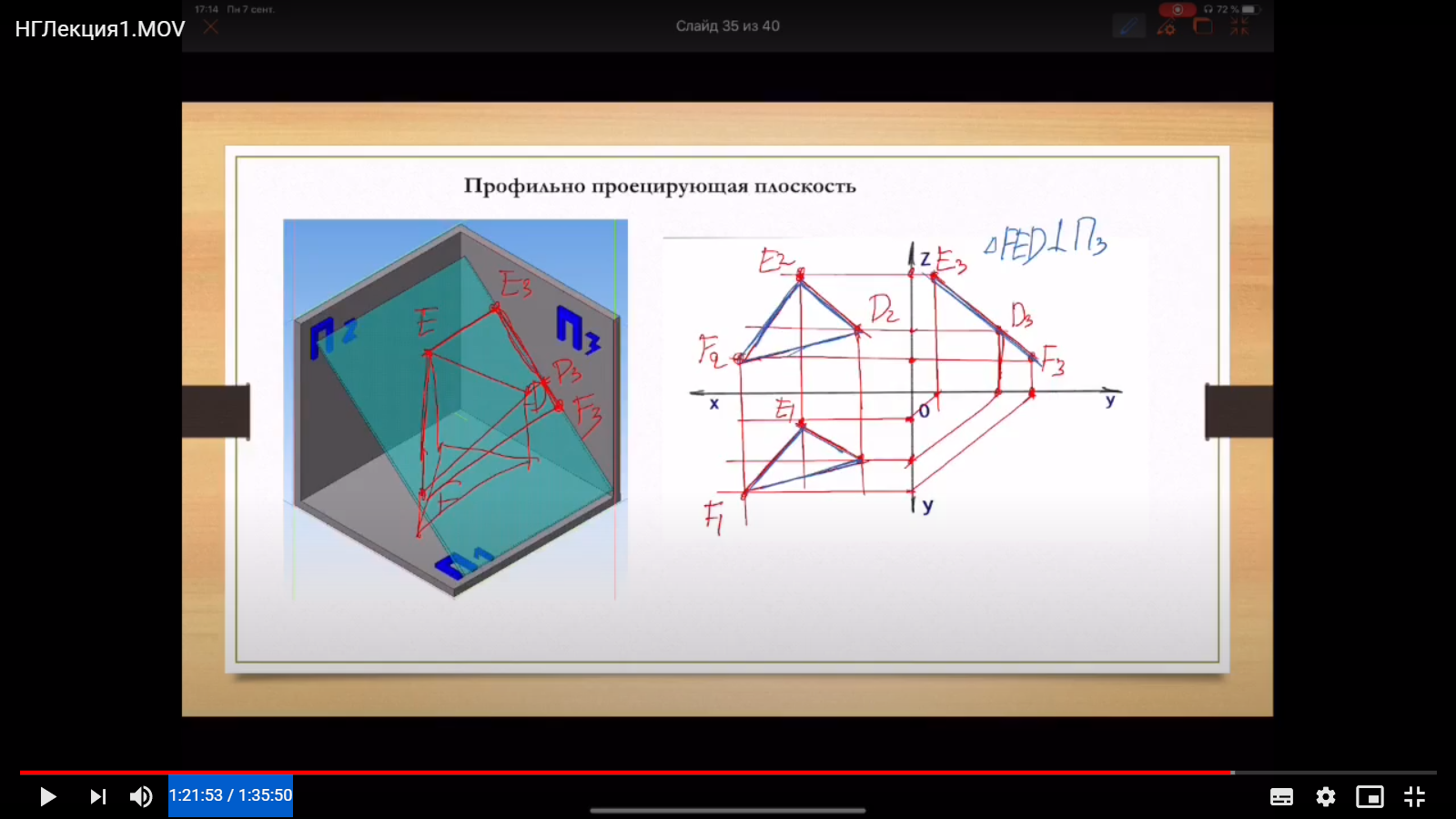 рофильно-проецирующая плоскость – плоскость, перпендикулярная к профильной плоскости проекций. Любой элемент этой плоскости, проецируется на профильную плоскость в прямую (профильный след плоскости).

Свойство проекций геометрических элементов, лежащих в проецирующих плоскостях. Проецирующая плоскость изображается прямой линией на той плоскости проекции, к которой она перпендикулярна.

Плоскость, перпендикулярная двум плоскостям проекций

Плоскости, перпендикулярные двум плоскостям проекций, параллельны третьей плоскости и называются плоскостями уровня или дважды проецирующими плоскостями.

Различают три плоскости уровня:

1 – горизонтальную плоскость [уровня] (параллельна пл-ти П1)

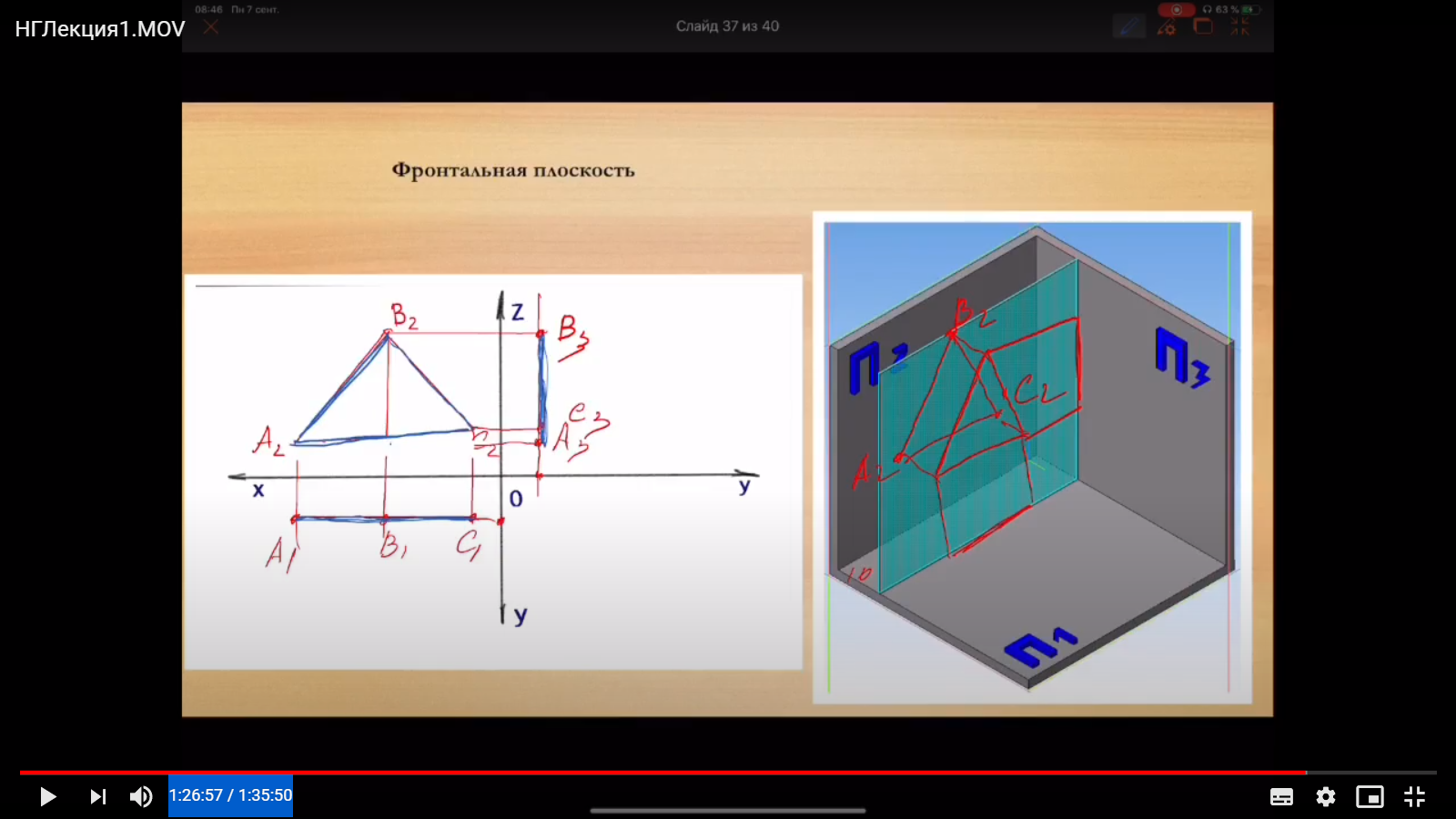
2 – фронтальную плоскость [уровня] (параллельна пл-ти П2)

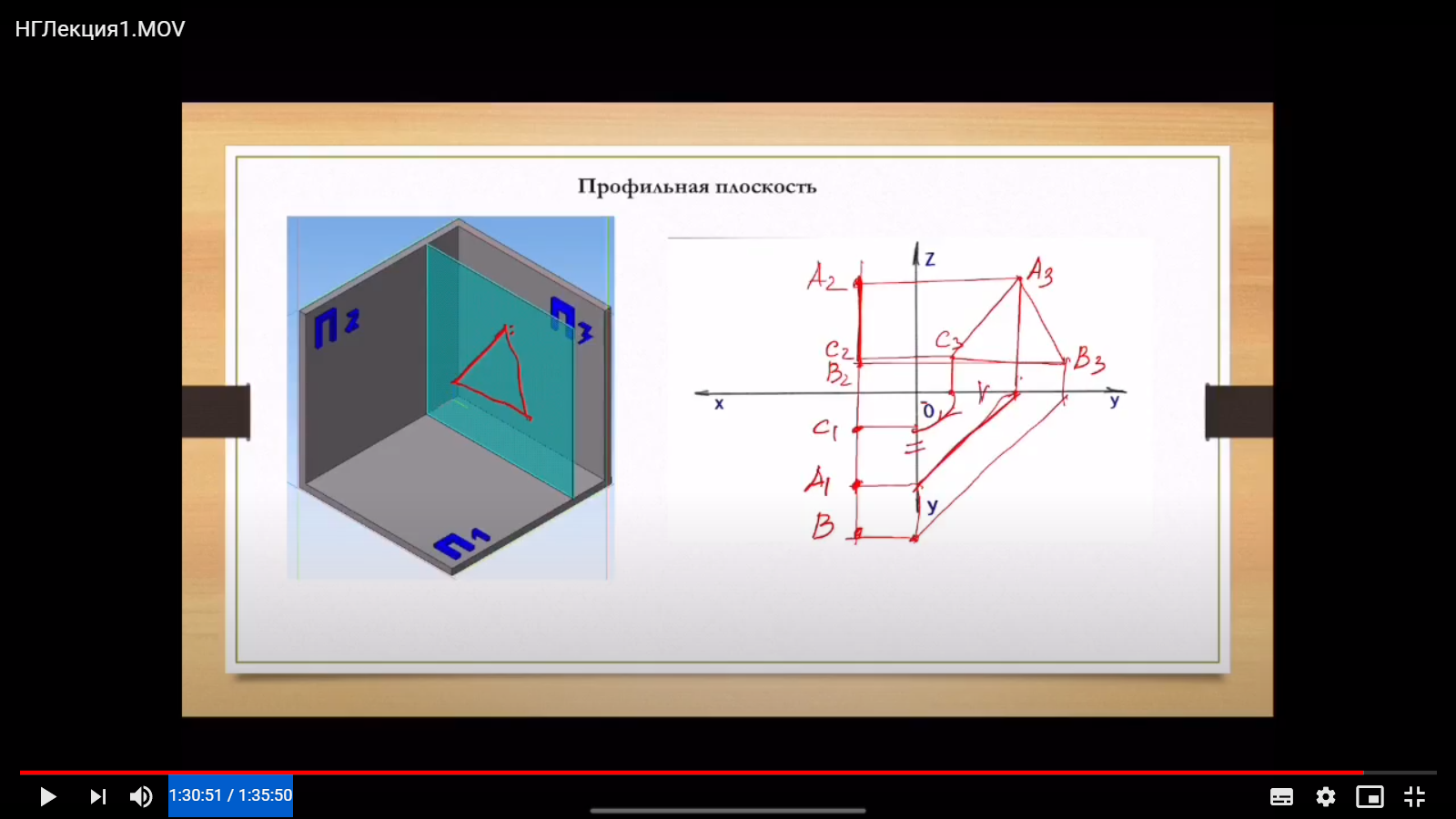3 – профильная плоскость [уровня] (параллельна пл-ти П3)

Любая линия (прямая или кривая), принадлежащая плоскости уровня, будет являться линией уровня. Любая фигура, лежащая в плоскости уровня, проецируется без искажения на плоскость проекций, ей параллельную.

[Любую линию (прямую или кривую), параллельную плоскости проекций, называют линией уровня. В инженерной графике различают три основные линии уровня: горизонталь, фронталь и профильную линии. ]