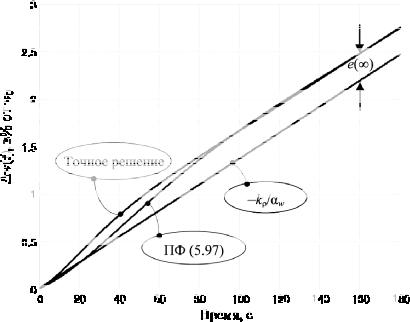
Рис. 5.24. Реакция мощности реактора на линейное увеличение реактивности
со скоростью 10-4 β/с при αw= –7,3·10-5 β/Вт, τ = 4,7 с, τ1 = 5,1 с, τ2 = 39,4 с,
τе=3,98 с. «Точное решение» получено путем численного интегрирования системы (5.1)–(5.5) в шестигрупповом приближении при Λ = 10-4 с,
λ= 0,0769 с-1, β=6·10-3
Взаключение отметим, что мы не затронули вопросы пространственной устойчивости, которые актуальны для реакторов с большими размерами активной зоны, например, РБМК. Конечно, в определенных случаях, когда оценки устойчивости по точечной модели дают значительные запасы устойчивости, можно предположить, что устойчивость будет обеспечиваться по всей активной зоне.
Устойчивость реактора можно исследовать как посредством расчета переходных процессов, возникающих вследствие управляющих воздействий, изменения нагрузки и возмущений технологических параметров в режимах нормальной эксплуатации и аварийных режимах, так и на основе критериев устойчивости, построением областей устойчивости в координатах технологических параметров. Уместно заметить, что построение областей устойчи-
281
вости требует значительных вычислительных ресурсов. Но при этом полученные результаты содержит не только ответ, устойчив реактор или нет, но и важнейшую информацию о запасах устойчивости.
Первые десятилетия атомной энергетики были характерны базовым режимом работы АЭС. В этом режиме основные агрегаты энергоблока и, в первую очередь, реактор работают на номинальном уровне мощности. При этом баланс генерируемых и потребляемых мощностей в электросети поддерживается в основном тепловыми электростанциями. Однако увеличение количества АЭС потребовало отхода от базового режима и участия атомных станций в регулировании мощности и частоты тока в энергосистеме. Обратные связи по температурам топлива, теплоносителя и замедлителя, давлению в активной зоне в случае устойчивого ректора приводит к возникновению его саморегулирования, в результате которого мощность реактора подстраивается в некоторых пределах под тепловую нагрузку. Если свойства саморегулирования не обеспечивают допустимую разность между требуемой и генерируемой в реакторе тепловой мощностью, приходится вводить дополнительные обратные связи по мощности реактора, давлению пара, температуре воды и др. в виде автоматического регулятора мощности, который посредством управляющих стержней обеспечивает дополнительное воздействие на реактивность, и поддерживает мощность реактора на требуемом уровне. Чем более выражены свойства саморегулирования реактора, чем точнее он отслеживает изменение тепловой нагрузки, тем проще система его управления.
Контрольные вопросы
1.В чем преимущества и недостатки модели мгновенного скачка при исследовании переходных процессов энергетического реактора? Справед-
ливо ли уравнение (5.8) для введенной в ректор реактивности ρ0 способом, отличным от ступеньки? Если ввести в реактор малую реактивность ρ0 мгновенно в виде ступеньки и медленно, например, линейно, изменится ли установившееся значение мощности?
2.В реактор с отрицательным мощностным эффектом ввели положительную реактивность при адиабатических условиях. Как зависит максимальная мощность и максимальная температура реактора от его теплоемкости?
3.Объясните понятие устойчивости динамической системы. Можно ли судить об устойчивости реактора по его поведению в подкритическом состоянии? Можно ли судить об устойчивости реактора по его поведению
вхолодном состоянии (на малых уровнях мощности)? Можно ли судить об устойчивости реального объекта по его линеаризованным уравнениям динамики?
4.Отрицательность мощностного коэффициента следует считать необходим, достаточным, или необходим и достаточным условием устойчивости реактора?
5.Преимущества и недостатки линеаризованных уравнений динамики. Что такое передаточная функция? В каких случаях переходный процесс, рассчитанный по передаточной функции, полностью совпадает с переходным процессом, рассчитанным по исходным дифференциальным уравнениям?
6.Дайте понятие саморегулирования реактора. Может ли иметь место саморегулирование реактора, если один из коэффициентов реактивности (все коэффициенты) является положительным? При каких условиях спра-
ведливо выражение (5.82) w = -ρ0/αw. Можно ли посредством этого уравнения описывать динамические процессы, или оно справедливо только для стационарного состояния?
7.При каких условиях можно моделировать поведение реактора во времени, используя только обратную связь реактивности по мощности реактора?
ПРИЛОЖЕНИЕ 1
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
При выполнении численных расчетов вручную без применения калькулятора или компьютера складывать или вычитать многозначные числа боле просто, чем их умножать и делить, тем более, возводить в степень или извлекать корень.
Если вместо каждого числа использовать его логарифм, то умножение и деление чисел можно заменить сложением и вычитанием их логарифмов, а возведение в степень и извлечение корня – умножением и делением соответственно. Логарифмы можно рассматривать как некоторые изображения чисел, применение которых упрощает выполнение операций над числами (оригиналами).
Подобно логарифмам существуют так называемые интегральные преобразования (Лапласа, Фурье, Ганкеля и др.) над функциями, которые позволяют операцию дифференцирования исходной функции (оригинала) заменить операцией умножения изображения этой функции на некоторый переменный (в общем случае комплексный), а операцию интегрирования заменить операцией деления. При этом решение обыкновенных дифференциальных уравнений сводится к решению алгебраических уравнений.
Оригинал и его изображение. Пусть имеется кусочно-
непрерывная функция F(t) действительного переменного t, заданная при t ≥ 0. Тогда можно ввести новую функцию
∞ |
|
F (s) = ∫ f (t)e−st dt, |
(П1.1) |
0 |
|
где s = a + jb – некоторое комплексное число (переменный преобразования Лапласа), называется изображением Лапласа функция F(t), а F(t) – оригиналом.
Можно показать, что несобственный интеграл (П1.1) сходится, если существуют такие действительные числа М и а0, что |F(t)| < < Mexp(a0t), т.е. если оригинал F(t) увеличивается с ростом t, то все же медленнее некоторой экспоненциальной функции. В этом случае между оригиналом и преобразованием существует взаимно однозначное прямое F(s) = L{F(t)} и обратное преобразование F(t) = = L-1{F(s)}. Заметим, что преобразование Лапласа существует для
выходных сигналов всех так называемых физических возможных систем*.
Основные свойства. Широкое практическое применение преобразования Лапласа обусловлено рядом полезных свойств.
1. Линейность. Пусть ci – числа, Fi(s) = L{Fi(t)} и
n |
|
f (t) = ∑ci fi (t), |
(П1.2) |
i=1 |
|
тогда |
|
n |
|
F(s) = ∑ci Fi (s). |
(П1.3) |
i=1
2. Изображение производной. Пусть F(s) = L{F(t)}, тогда
L= sF(s) − f (0).
dt
3.Изображение интеграла. Пусть F(s) = L{F(t)}, тогдаdf (t)
t |
|
|
F(s) |
|
|
|
|
|
|
L |
|
f (τ)dτ |
= |
|
. |
|
s |
∫ |
|
|
|
|
0 |
|
|
|
|
4.Масштабирование независимого переменного. Пусть F(s) =
=L{F(t)} и a – число, тогда
L{ f (at)} = |
1 |
F |
|
s |
. |
(П1.6) |
|
|
|
a |
|
|
|
|
|
a |
|
5. |
Начальное значение оригинала. Пусть F(s) = L{F(t), тогда |
|
lim |
f (t) = lim sF (s). |
(П1.7) |
|
x→0+ |
s→∞ |
|
6. |
Установившееся значение оригинала. Пусть F(s) = L{F(t), то- |
гда |
lim f (t) = lim sF (s). |
(П1.8) |
|
|
x→∞ |
s→0 |
|
Изображения некоторых функций. Изображения часто встре-
чающихся функций приведены в табл. П1**.
*Под физически возможной системой понимают такую систему (объект), реакция любого выхода которой появляется не раньше входного воздействия, вызвавшего эту реакцию (переходный процесс).
**Более подробные таблицы преобразования Лапласа см.: Корн Т., Корн Г. Справочник по математике для научных работников и инженеров. М.: Наука, 1973.
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица П1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оригинал F(t) |
Изображение F(s) = L{F(t)} |
|
1(t), 1 при t ≥ 0 и 0 при t < 0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tn |
|
|
|
|
|
n! |
|
|
|
|
|
|
|
sn+1 |
|
|
|
|
|
|
|
|
|
e-at |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
s + a |
|
|
|
|
|
|
|
|
te-at |
|
|
|
1 |
|
|
|
|
|
|
|
(s + a)2 |
|
|
|
sin(at) |
|
|
|
|
|
|
a |
|
|
|
|
s2 + a2 |
|
|
|
|
|
|
cos(at) |
|
|
|
|
|
|
s |
|
|
|
|
s2 + a2 |
|
|
|
|
|
|
n |
|
|
n |
|
|
d n |
|
|
t F(t) |
(−1) |
|
|
|
|
F(s) |
|
|
|
|
|
dsn |
|
∫t |
f1 (τ) f2 (t −τ)dτ |
F1(s)F2(s) |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычисление оригинала по известному изображению. Если в таблице преобразований отсутствует требуемая функция, то оригинал по известному изображению на практике наиболее часто можно рассчитать посредством формулы разложения. Изображения реакции выхода динамической системы, как правило, представляют рациональную дробь:
F(s) = |
M (s) |
= |
b sm +b |
|
sm−1 |
+... +b s +b |
, |
n > m. (П1.9) |
|
m |
m−1 |
|
1 |
0 |
N (s) |
a sn + a |
|
|
+... + a s + a |
|
|
n−1 |
sn−1 |
|
|
|
|
|
n |
|
|
1 |
0 |
|
|
В этом случае оригинал F(t) = L-1{F(s)} найден по формуле:
p |
M (sk ) |
|
1 |
|
r−1 |
|
M (s)(s − sr ) |
r |
e |
st |
|
f (t) = ∑ |
esk t + |
|
d |
|
|
|
|
, (П1.10) |
' |
|
r −1 |
N (s) |
|
|
|
k =1 |
N (sk ) |
(r −1)! ds |
|
|
|
|
s=s |
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
где s1… sp – p простых корней и sr – корень кратности r характеристического уравнения N(s) = 0.
Пример 1. Найдем приращение мощности критического реактора, представленного посредством ПФ (5.51) в одногрупповом приближении (n = 1, ρ0 = 0), вызванное скачком реактивности Δρ (Δρ(s) = Δρ/s). Тогда в соответствии с (5.50) изображение приращения мощности
|
w(s) = |
w0 (s +λ) |
Δρ, |
(П1.11) |
|
s2 (Λs + a) |
|
|
|
|
где a = λΛ + β.
Сравнив последнее выражение с (П1.9), отмечаем, что M(s) =
= w0Δρ(s + λ) и N(s) = (Λs + a)s2. Приравняем N(s) к нулю и найдем корни характеристического уравнения: s1 = – a/Λ (p = 1) и s2 = 0 (r = 2),
затем производную характеристического уравнения dN(s)/ds = 3Λs2 + + 2as. Тогда в соответствии с (П1.10):
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w0Δρ |
λ − |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
st |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Λ |
|
− |
|
|
t |
|
|
|
|
d (s +λ)s |
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w(t) = |
|
|
|
|
|
|
|
|
|
|
e |
Λ |
|
+ w0Δρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
a |
2 |
|
|
|
|
a |
|
|
|
|
2 |
(Λ + a) |
|
3Λ |
|
−2a |
|
|
|
|
|
|
|
|
|
|
ds |
s |
|
s=0 |
|
|
Λ2 |
|
Λ |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(a −λΛ)(1−e− |
|
t ) +λat |
|
|
|
|
|
|
|
|
= w |
Δρ |
Λ |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Заменив в (П1.12) а на λΛ+β, окончательно получим: |
|
|
|
|
|
|
w |
|
Δρ |
|
|
|
β |
|
|
|
|
− |
λ+ |
β |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w(t) |
= |
|
0 |
|
|
|
|
|
|
|
|
|
1−e |
|
Λ |
+λt |
. |
|
|
λΛ +β |
λΛ +β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2. Найдем решение дифференциального уравнения для предшественников запаздывающих нейтронов (1.49):
dсdt(t) = βэффΛn(t) −λс(t) .
После перехода к изображениям переменных n(t) и с(t) получим
(1.50): |
|
|
|
|
βэффn(s) |
|
|
|
sc(s) −c(0) = −λс(s) + |
|
, |
|
|
|
Λ |
|
|
|
откуда |
|
|
|
|
|
|
|
|
βэфф |
|
|
|
|
|
|
|
|
c(s) = |
1 |
n(s) + |
c(0) |
. |
(П1.14) |
Λ |
|
s + λ |
s +λ |
|
|
|
|
|
|
Для нахождения оригинала c(t) для (П1.14) применим формулу умножения изображений (см. 8-я строку табл. П1) к первому слагаемому (П1.14) и изображение экспоненты (см. 3-ю строку табл. П1), тогда
|
|
β |
эфф |
t |
|
|
c(t) = |
|
∫e−λ(t-t′) n(t′)dt′+ c(0)e−λt . |
(П1.15) |
|
Λ |
|
|
0 |
|
Пока n(t) задана в общем виде, интеграл в (П1.15) не может быть вычислен, а само выражение представляет интегральную форму уравнения (1.49).
Если предположить, что до t = 0 имело место стационарное состояние рекактора, то c(0) = βэффn(0)/(λΛ), и тогда (П1.15) можно записать в виде.
|
β |
эфф |
t |
β |
эфф |
|
|
c(t) = |
|
∫e−λ(t −t′) n(t′)dt′+ n(0) |
|
e−λt . |
(П1.16) |
|
|
|
|
|
Λ |
0 |
λΛ |
|
Исходное уравнение (1.49) является линейным неоднородным дифференциальным уравнением 1-го порядка. Его решение (П1.16) состоит из суммы частного решения неоднородного уравнения (первое слагаемое) – принужденная составляющая решения и общего решения однородного уравнения (второе слагаемое, зависящее от начальных условий) – свободная составляющая.
Как следует из (П1.16), при t > (3÷5)·λ-1 из-за свойств экспоненты начальное условие n(0) перестает оказывать влияние на c(t), т.е. реактор (система) «забывает» о начальном состоянии. При этом c(t) определяется n(t), и имеет значение только принужденная составляющая.
В случае, когда интерес представляет только принужденная составляющая решения, (П1.16) можно упростить и представить в виде
|
|
β |
эфф |
t |
|
|
c(t) = |
|
∫ e−λ(t −t′)n(t′)dt′. |
(П1.17) |
|
Λ |
|
|
−∞ |
|
В (П1.17) начальные условия бесконечно отдалены (перенесены в прошлое) и к текущему моменту времени t > 0 поведение системы зависит только от ее параметров и воздействия n(t).
ПРИЛОЖЕНИЕ2
Некоторые пассивные способы компенсации реактивности
В процессе работы реактора происходит почти линейная во времени потеря реактивности, если в реакторе нет выгорающих поглотителей. Добавление в реактор выгорающих поглотителей существенно изменяет временной ход потери реактивности. Если появление положительной реактивности в результате выгорания поглотителя будет иметь близкую к линейной зависимость от времени, то в целом изменение реактивности реактора (из-за выгорания топлива и поглотителя) может мало отличаться от нулевого значения. Именно в таком случае можно реализовать саморегулирование реактора в течение всей кампании и не использовать систему управляющих поглощающих стержней. В данном приложении рассмотрены несколько вариантов пассивных способов компенсации потери реактивности.
Гомогенные выгорающие поглотители. Проанализируем на качественном уровне действие гомогенного выгорающего поглотителя. Пусть реактор после вывода на номинальный уровень мощности находится в критическом состоянии. Пусть его запас реактивности скомпенсирован введенным борным поглотителем. И этот запас реактивности составляет ρВ. Пусть темп потери реактивности из-за выгорания топлива постоянен во времени и полная потеря реактивности за кампанию Т равна ρвыг. Будем полагать, что сечение поглотителя sа не изменяется во времени, что возможно при низких концентрациях ядер поглотителя, таких, что можно пренебречь блокировкой сечений.
Если поглотитель со средним независимым от времени сечением поглощения нейтронов σа разместить в материалах активной зоны, то при отсутствии блокировки сечений изменение количества ядер поглотителя во времени Na(t) можно записать в виде
dNa(t)/dt = – σaϕ(t)Na(t). |
(П2.1) |
Имеет смысл ввести переменную в виде эффективного времени τ = ϕ(t)t, поскольку плотность потока нейтронов может являться функцией времени, если реактор работает на постоянном уровне
мощности; ϕ – это средняя по реактору плотность потока нейтронов.
Количество ядер поглотителя будет изменяться по очевидному
экспоненциальному закону: |
|
Na(τ) = Na(0)exp(–σaτ), |
(П2.2) |
где Na(0) – начальное количество ядер поглотителя; Na(τ) – количество ядер поглотителя в момент времени t = τ/ϕ.
Реактивность ρВ, которую вносит выгорающий поглотитель, в первом приближении пропорциональна количеству ядер (при отсутствии блокировки) поглотителя. Скорость выгорания поглотителя не зависит от его массы, но зависит от сечения поглощения и плотности потока нейтронов. Следовательно, по мере выгорания ядер поглотителя будет появляться положительная реактивность
ρ+(τ) = ρВ[1 – Na(τ)/Na(0)] = ρВ[1 – ехр(–σaτ)]. |
(П2.3) |
Таким образом, вычисление роста реактивности ρ+(τ) по мере выгорания поглотителя определяется зависимостью Na(τ)/Na(0). Рассмотрим различные приближения для нахождения Na(τ)/Na(0).
В реакторах типа РБМК, где реализована непрерывная перегрузка топлива, плотность потока нейтронов можно считать постоянной во времени. В таком случае σаτ = σаϕоt, выгорание поглотителя происходит по экспоненциальной зависимости ехр(–σаϕоt), и положительная реактивность растет в реальном времени по зако-
номерности: |
|
ρ+(t) = ρВ[1 – Na(τ)/Na(0)] = ρВ[1 – ехр(–σаϕоt)]. |
(П2.4) |
В энергетических реакторах ВВЭР и БН, в транспортных реакторах, в которых перегрузка происходит после достижения достаточно глубоких значений выгораний, для поддержания постоянного уровня мощности необходимо потребовать, чтобы было постоянным во времени произведение макроскопического сечения деле-
ния на плотность потока нейтронов, т.е. |
|
Σf (0)ϕ(0) = Σf (t)ϕ(t). |
(П2.5) |
Поэтому из-за изменения макроскопического сечения деления (выгорание топлива) для поддержания постоянного уровня мощности требуется изменять плотность потока нейтронов. Отношение ϕ(t)/ϕ(0) можно найти из (П2.5) и (П2.1) для конкретного случая.
Пусть в реакторе используется урановое топливо с высоким обогащением, тогда можно пренебречь вкладом в мощность обра-