Добавил:

Rumpelstilzchen Rumpelstilzchen2018@yandex.ru Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

МИРЭА - Российский технологический университет

Предмет:

Математический анализ

Файл:

3-й семестр / Лекции / 13

.pdf

Скачиваний:

Добавлен:

25.12.2020

Размер:

530.22 Кб

Скачать

☆

ЛЕКЦИЯ 13

4.3. Ряд Лорана, его область сходимости.

Определение 4.6. Рядом Лорана называется ряд вида

. . . +

−

+. . . +

−1

( −

)

−

( − )

+ ( − )2

+. . . +

( − ) +. . . =

∞0

∞

= ∑ ( − ) +

∑

−

( −

)

Где ,

– комплексные постоянные, а – комплексная переменная.

Ряд Лорана сходится в области, в которой сходятся ряды

∞	−			−1		−2
∑			=		+			+. ..
	( −	)		−		( −	)2
=1	0			0		0

∞

∑ ( − 0) = 0 + 1( − 0) + 2( − 0)2+. ..

Областью сходимости ряда первого из этих рядов является внешность круга | − 0| > . Областью сходимости ряда второго ряда является внутренность круга | − 0| < .

Если < , то ряд сходится в кольце < | − 0| < .

Здесь ≥ 0, 0 < < +∞.
Теорема 4.4. Функция ( ) однозначная		и аналитическая в кольце <
\| − 0\| < (не исключаются случаи = 0		и = +∞) разлагается в этом
кольце в ряд Лорана
	∞
( ) =	∑ ( − ) =
		0

=−∞

−1 ∞

=	∑			( −		) + ∑		( − ) ,
				0				0
	=−∞						=0
где коэффициенты находятся по формулам

	=	1	∫		( )		( = 0, ±1, ±2, . . . )
	=	2	∫				( = 0, ±1, ±2, . . . )
		2	( − ) +1
				0

Здесь – произвольная окружность с центром в точке 0, лежащей внутри данного кольца.

На практике при нахождении коэффициентов стараются избежать применения этих формул, так как они приводят к громоздким вычислениям.

Чаще используют готовые разложения в ряд Тейлора элементарных функций.

4.3. Примеры разложения функций в ряд Лорана

Пример 4.2.

Разложить в ряд Лорана функцию ( ) = ( − 3)4

в окрестности

−3

точки 0 = 3.

Решение: сделаем замену

получим

( ) =

. Используя

−3

разложение (4.3), получим

= 1 −

−

+. . .,

− 3

2! ( − 3)2

4! ( − 3)4

6! ( − 3)6

тогда

( ) = ( − 3)4 (1

−

2! ( − 3)2

4! ( − 3)4

( − 3)6

+. . . ) = ( − 3)4

( − 3)2

−

+. ..

( − 3)2

Это разложение справедливо

для

любой

точки

≠ 3.

данном случае

«кольцо» представляет собой всю комплексную плоскость с одной выброшенной точкой = 3. Его можно определить так: 0 < | − 3| < +∞. Здесь = 0, = +∞. В указанной области ( ) – аналитическая.

Пример 4.3.

Получить все разложения в ряд Лорана по степеням функции ( ) =

2 +3 .2+3 +2

Решение: Приравняем знаменатель дроби к нулю 2 + 3 + 2 =

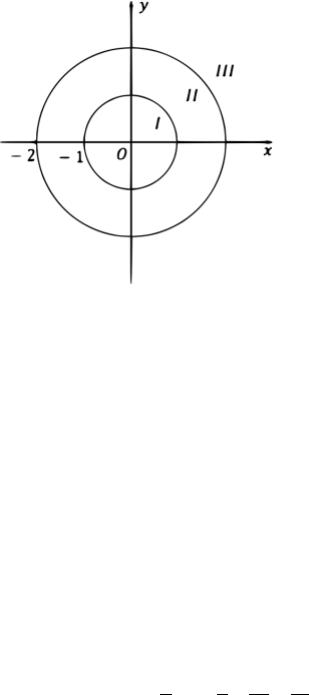
( + 2)( + 1) = 0, отсюда 1 = −2, 2 = −1. Изобразим на комплексной плоскости возможные области. Для этого проведем окружности с центром в0 = 0 и радиусом равным расстоянию до ближайшей особой точки. Имеем три «кольца» с центром в точке 0 = 0, в каждом из которых ( ) является аналитической:

1)круг | | < 1,

2)кольцо 1 < | | < 2,

3)2 < | | < +∞ – внешность круга | | ≤ 2 (см. рис.)

Найдем ряды Лорана для функции ( ) в каждой из этих областей. Для

этого представим ( ) в виде суммы элементарных дробей

( ) =	2 + 3	=		+		=	1	+	1	.

	2 + 3 + 2		+ 1		+ 2		+ 1		+ 2

и нашли методом неопределенных коэффициентов.

1) Рассмотрим круг | | < 1. Преобразуем ( ):

( ) =	1	+	1	1		.

	1 +		2	1 +
					2

Используя формулу (4.6), получим

1 2 3( ) = (1 − + 2 − 3+. . . ) + 2 (1 − 2 + 22 − 23 −. . . ) =

= 32 − 32 + 54 2 − 98 3+. ..

Это разложение является рядом Тейлора функции ( ), при этом ряд для
функции	1	= 1 − + 2−. .. сходится при \| \| < 1, а
функции	1+	= 1 − + 2−. .. сходится при \| \| < 1, а
	1+
		1	= 1 −		+	2	−	3	+. ..
			= 1 −	2	+	4	−	8	+. ..
		1 + 2		2		4		8
		1 + 2

сходится при |

2) Рассмотрим

кольцо 1 < | | < 2.

Ряд

для

функции

остается

сходящимся в этом кольце, т.е. | | < 2, а ряд для функции

расходится при

| | > 1. Поэтому преобразуем ( ) следующим образом

( ) =

1 +

Применяя формулу (4.6), получаем

( ) =

(1 −

−

+. . . ) +

(1 −

−

+. . . )

−

+. . . +

−

+. . .

Этот ряд сходится для |

| < 1, т.е. при | | >

и при | | < 2.

3) Рассмотрим | | > 2. Ряд для функции

при | | > 2 расходится, а ряд

> 2,

> 1

для функции

сходится,

если

то условие

выполняется.

1+1

Представим ( ) в виде

( ) =

1 +

Используя формулу (4.6), получим

( ) =

(1 −

−

+. . . ) +

(1 −

−

+. . . )

(2 −

−

) =

−

+. ..

Т.е. для разных областей ряд Лорана функции ( ) имеет разный вид.

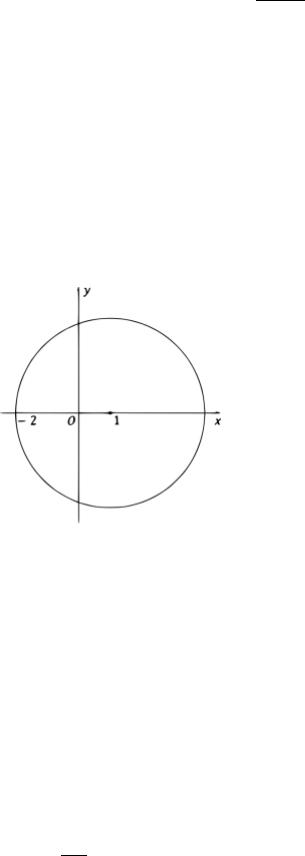
Пример 4.4. Разложить в ряд Лорана функцию ( ) = 2 +1 в окрестности

2+ −2

0 = 1.

Решение: найдем особые точки функции ( ), для этого приравняем знаменатель к нулю 2 + − 2 = 0, 1 = 1, 2 = −2, т.е. разложение необходимо осуществить в окрестности особой точки 1 = 1, т.е. в кольце

0 < | − 1| < 3. Число 3 найдено, как расстояние между центром разложения

= 1 и ближайшей особой точкой = −2 (см. рис.).

Представим ( ) в виде суммы элементарных дробей
	2 + 1	=		+		=	1	+	1	.

	2 + − 2		− 1		+ 2		− 1		+ 2

Введем новую переменную − 1 = , т.е. = + 1 и перепишем функцию


1	=	1		=	1		1		=	1			1		. Используя разложение (4.6), получим

+2		+3			3					3
						1+					1+			−1
						1+					1+
								3			3
				1		=	1				1				=	1	[1 −	− 1	+	( − 1)2	−	( − 1)3	+. . . ]
			+ 2			=	3		1 +			− 1			=	3	[1 −	3	+	9	−	27	+. . . ]
												3

Область сходимости этого ряда | −31| < 1 или | − 1| < 3. Таким образом,

разложение в ряд Лорана в кольце 0 < | − 1| < 3 имеет вид

( ) =

2 − 1

− 1

( − 1)2

( − 1)3

−

+. ..

2 + − 2

− 1

Слагаемое

является

степенью

( − 1)−1 и

поэтому

не требует

−1

дальнейшего разложения.

Соседние файлы в папке Лекции

#
25.12.20201.36 Mб311 - презентация.pdf
#
25.12.2020548.46 Кб311.pdf
#
25.12.2020804.68 Кб212 - презентация.pdf
#
25.12.2020751.91 Кб512.pdf
#
25.12.2020852.96 Кб313 - презентация.pdf
#
25.12.2020530.22 Кб313.pdf
#
25.12.2020793.25 Кб314 - презентация.pdf
#
25.12.2020519.02 Кб314.pdf
#
25.12.2020707.51 Кб315 - презентация.pdf
#
25.12.2020532.12 Кб315.pdf
#
25.12.2020859.93 Кб316 - презентация.pdf