Добавил:

Rumpelstilzchen Rumpelstilzchen2018@yandex.ru Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

МИРЭА - Российский технологический университет

Предмет:

Математический анализ

Файл:

3-й семестр / Лекции / 12

.pdf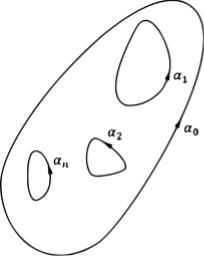

Скачиваний:

Добавлен:

25.12.2020

Размер:

751.91 Кб

Скачать

☆

ЛЕКЦИЯ 12

3.2. Теорема Коши. Интегральная формула Коши.

Теорема 3.1. (теорема Коши для односвязной области). Если ( ) – аналитическая функция в односвязной области и – замкнутый контур, принадлежащий области , то интеграл не зависит от пути интегрирования и

			( ) = 0,			(3.4)
			( ) = 0,

	Определение 3.1. Линия называется связной, если из любой ее точки
можно пройти по этой линии в любую другую ее точку.
	Определение 3.2.		Порядком	связности	ограниченной	области
называется число связных частей, на которое разбивается ее граница.
	Например, круг \| \| ≤ 3 – односвязная область, а кольцо					1 ≤ \| \| ≤ 3	–
двусвязная область.
	Теорема 3.2. (теорема Коши для многосвязной области) Если функция
( )
( )		аналитична в	замкнутой	области	, ограниченной кривыми
	,	, . . . , , то интеграл от ( )		по внешнему контуру		равен сумме
0	1				0

интегралов по внутренним контурам при условии, что обход всех контуров совершается в одном направлении

			∫ ( )	= ∫ ( ) +. . . + ∫		( ),	(3.5)

			0	1
где	,	, . . . ,	обходится	в одну сторону,	например, против		часовой
0	1

стрелки (см. рис. 15).

Рис. 1

Теорема 3.3. (интегральная формула Коши) Если – односвязная или многосвязная область, ограниченная контуром , и ( ) – однозначная и


аналитическая в функция, тогда		для любой точки				0 справедлива
формула
	(0) =	1	∫	( )	.	(3.6)
		2		− 0

Теорема 3.4. Если функция ( ) аналитична в области и непрерывна в

, то во всех внутренних точках области у функции ( ) существуют производные любого порядка, причем справедлива формула

( )( ) =	!	∫	( )		,	(3.7)
	2		( −	) +1
0
			0

где 0 , а – граница области .

Формулой (3.7) можно пользоваться для вычисления некоторых интегралов.

Пример 3.3.


Вычислить интеграл ∫							, если
Вычислить интеграл ∫						2−4	, если
1) : \| − 1\| =	1	, 2)			: \| − 1\| = 2,			3) : \| − 1\| = 4.
1) : \| − 1\| =	2	, 2)			: \| − 1\| = 2,			3) : \| − 1\| = 4.
	2
Решение:
1) : \| − 1\| =			1	.	В замкнутой			области, ограниченной окружностью
1) : \| − 1\| =				.	В замкнутой			области, ограниченной окружностью
	2

| − 1| = 12, подынтегральная функция аналитическая, т. к. точки, в которых

знаменатель обращается в нуль 1 = 0 , 2 = 4 не входят в область. Тогда по теореме Коши (3.1)

∫ = 0.

| −1|=12 2 − 4

2) : | − 1| = 2. Внутри области, ограниченной окружностью | − 1| = 2, находится одна точка 1 = 0, в которой знаменатель обращается в нуль. Перепишем интеграл в виде



∫			= ∫	− 4	.


	2	− 4
\| −1\|=2	2	− 4	\| −1\|=2
\| −1\|=2			\| −1\|=2

Функция ( ) = является аналитической в данной области.

−4

Применяя интегральную формулу Коши (0 = 0) (3.6), получим

∫

= 2 (

) |

= 2 (−

) = −

− 4

| −1|=2

3) : | − 1| = 4. В области, ограниченной окружностью | − 1| = 4, имеем две точки 1 = 0, 2 = 4 в которых знаменатель подынтегральной функции обращается в нуль. Применить сразу формулу (3.6) нельзя. Решить задачу можно двумя способами.

1 способ. Разложим дробь						1				на простейшие, получим

					2−4
					2−4
						1					=		+		,

				2 − 4								− 4
Найдем и любым способом (например, методом неопределенных
коэффициентов). =	1	, = −					1	, т.е.
коэффициентов). =	4	, = −						, т.е.
	4					4
	1										1	1		1	1
									=				−			.
			2 − 4						=		4	− 4	−	4		.

Подставляя в интеграл, получим

∫

−

∫

| −1|=4 ( − 4)

| −1|=4 − 4

| −1|=4

2 ( ) |

2 ( )

( 4

1) =

( 4

− 1)

−

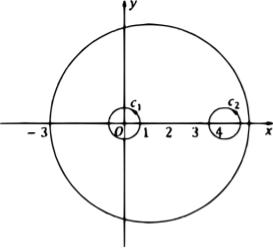
2 способ. Построим окружности 1

и 2

с центром в точках 1 = 0 и 2 = 4

настолько малых радиусов, чтобы окружности 1

2 не пересекались и

целиком лежали в круге | − 1| ≤ 4.

В трехсвязной области, ограниченной

окружностями

| − 1| = 4,

1, 2 подынтегральная

функция

аналитична.

Тогда по теореме 3.2. Коши для многосвязной области (см. рис. 16)

∫

= ∫

+ ∫

| −1|=4 ( − 4)

( − 4)

Рис. 2

К каждому интегралу в правой части применим интегральную формулу Коши (3.6). Получим

∫

= 2 (

)

+ 2 (

) |

( − 4)

− 4

|−1|=4

(4 − 1)

= 2 (−

) + 2

Получен тот же результат, что и первым способом.

Пример 3.4.

Вычислить интеграл ∫| |=1

( −

)

Решение:

точка

принадлежит кругу | | < 1. Применим формулу

(3.7), ( ) = 2

∫

( 2 )′′ |

= 4 (− 2 ) |

= −4 .

| |=1 ( −

)

Тема 4. Ряды с комплексными членами. Ряды Тейлора и Лорана

4.1. Числовые ряды с комплексными членами

4.2.Ряд Тейлора. Коэффициенты ряда. Разложение функции, аналитической в круге, в степенной ряд.

Пусть дана последовательность функций комплексной переменной

1( ), 2( ), … , ( ), …, определенных на некотором множестве D комплексной плоскости: . Выражение вида

1( ) + 2( ) + + ( ) + = ∑∞=1 ( )

называется функциональным рядом с комплексными членами.

Определение 4.4. Множество значений переменной z, при которых функциональный ряд сходится, называется областью сходимости функционального ряда.

Определение 4.5. Ряд вида

0 +∞ 1( − 0) + 2( − 0)2+. . . + ( − 0) +. . . = = ∑ ( − 0) ,

где и 0 – комплексные постоянные, а – комплексная переменная, называется степенным рядом в комплексной области.

При 0 = 0 степенной ряд имеет вид ∑∞=0 = 0 + 1 + 2 2 + .

Теорема 4.2 (теорема Абеля). Пусть степенной ряд

Теорема 4.3. Функция ( ) аналитична в круге | − 0| < , разлагается в нем единственным образом в сходящийся к ней степенной ряд Тейлора

∞

( ) = ∑ ( − 0) ,

коэффициенты которого вычисляются по формулам

	1		( )			( )(	)
=		∫			=	0		( = 0,1, . . . ),
=	2	∫		) +1	=	!		( = 0,1, . . . ),
	2	( −		) +1		!
			0

где – окружность с центром 0, целиком лежащая в круге сходимости ряда | − 0| < .

Предполагается, что окружность проходится в положительном направлении, т.е. против часовой стрелки.

Имеют место следующие разложения в ряд Тейлора в окрестности точки

0 = 0.

= 1 + +

+. . . +

+. . . = ∑∞

, = ∞,

сх

sin = −

+ + (−1)

2 +1

+ =

∑∞

2 +1

(2 +1)!

=0 (2 +1)!

сх

= 1 −

+. . . +(−1)

+. . . = ∑∞

(−1)

(2 )!

сх

(1 + ) = −

− + (−1)−1

+ =

= ∑=1∞ (−1)−1

, сх = 1,

(1 + ) =

1 + +

( −1)

2+. . . +

( −1)...( − +1)

+. ..,

при = −1,

1+1 = 1 − + 2−. . . +(−1) +. . . = ∑∞=0(−1) ,сх = 1,

=∞,

сх = 1

(4.1)

(4.2)

(4.3)

(4.4)

(4.5)

(4.6)

1	= 1 + + 2+. . . + +. . . = ∑∞	, = 1.	(4.7)

1−	=0	сх

Пример 4.1.

Разложить по степеням ( − 2) функцию ( ) = 7−12.

Решение: введем новую переменную = − 2, выразим = + 2 и подставим в функцию ( )

( ) =	1	=	1	=	1	1

	7 − 2( + 2)		3 − 2		3	1 −	2
							3

в точке = 2 ( = 0). Воспользуемся формулой (4.10), подставляя вместо

→ 23 :

	1					1				1							2	2			2		2
( ) =									=			(1 +						+ (		)	+. . . + (				)	+. . . ).
( ) =		3		1 − 2					=		3	(1 +					3	+ (	3	)	+. . . + (			3	)	+. . . ).
						3
Сделаем обратную замену
( ) =	1		[1 +				2	( −		2)			+	22			( − 2)2+. . . +					2	( − 2) +. . . ].
( ) =	3		[1 +			3		( −		2)			+	32			( − 2)2+. . . +					3	( − 2) +. . . ].
	3					3								32								3
Этот ряд сходится при условии \|															2	( − 2)\| < 1, или							\| − 2\| <				3	, т.е. радиус
Этот ряд сходится при условии \|																( − 2)\| < 1, или							\| − 2\| <					, т.е. радиус
					3									3												2
сходимости ряда =					3		.
сходимости ряда =					2		.
					2

Соседние файлы в папке Лекции

#
25.12.2020742.36 Кб309.pdf
#
25.12.2020648.94 Кб310 - презентация - примеры.pdf
#
25.12.20201.36 Mб311 - презентация.pdf
#
25.12.2020548.46 Кб311.pdf
#
25.12.2020804.68 Кб212 - презентация.pdf
#
25.12.2020751.91 Кб512.pdf
#
25.12.2020852.96 Кб313 - презентация.pdf
#
25.12.2020530.22 Кб313.pdf
#
25.12.2020793.25 Кб314 - презентация.pdf
#
25.12.2020519.02 Кб314.pdf
#
25.12.2020707.51 Кб315 - презентация.pdf