
3-й семестр / Лекции / 13 - презентация
.pdf
|
|
|
|
( |
) |
|
2 +1 |
|
|
Пример 3. |
Разложить в ряд Лорана функцию |
|
= |
2+ −2 |
в |
||||
окрестности 0 = 1. |
|
|
|
|
|
|
|
||
Найдем особые точки функции |
, для этого приравняем |
|
|
|
|||||
|
|
( |
) |
|
|
|
|
|
|
знаменатель к нулю 2 + − 2 = 0, |
= 1, = −2, т.е. разложение |
||||||||
|
|
|
1 |
2 |
|
|
|
|
|
необходимо осуществить в окрестности особой точки 1 = 1, т.е. в |
|
||||||||
кольце 0 < |
| |
− 1 < 3. Число 3 найдено, как расстояние между |
|
||||||
|
| |
|
|
|
|
|
|
|
|
центром разложения = 1 и ближайшей особой точкой = −2 (см.
рис.)
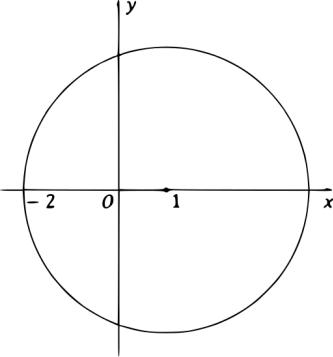
Представим ( ) в виде суммы элементарных дробей
2 + 1 |
= |
|
+ |
|
= |
1 |
|
+ |
1 |
. |
||
|
|
|
|
|
|
|
|
|||||
2 + − 2 |
− 1 |
+ 2 |
− 1 |
+ 2 |
||||||||
Первое слагаемое – дробь, содержащая ( − 1)−1. Дальнейшего
разложения не требует.
Введем новую переменную − 1 = , т.е. = + 1 и перепишем
функцию |
|
1 |
|
= |
1 |
|
= |
1 |
|
|
1 |
|
= |
1 |
|
|
|
1 |
. Используя табличное |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
−1 |
||||||||||||||||||||||||||||||
|
|
|
+2 |
|
|
+3 |
3 |
|
|
1+ |
|
|
3 |
|
|
1+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
разложение, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
|
|
1 |
1 |
|
|
|
|
1 |
|
|
|
|
|
− 1 |
|
( |
|
)2 |
|
( |
)3 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
− 1 |
|
|
− 1 |
|
|
|||||||||||||||||||||||
|
|
= |
|
|
|
|
|
|
|
|
= |
|
[1 − |
|
|
|
|
+ |
|
|
− |
|
|
|
|
+. . . ] |
||||||||||||||
|
+ 2 |
3 |
1 + |
− 1 |
3 |
|
3 |
|
9 |
|
|
|
27 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Область сходимости этого ряда |
| |
−1 |
| < 1 |
или |
| |
− 1 |
| |
< 3. Таким |
||||||||||||||||||||||||||||||||
|
3 |
|
|
|
|
|||||||||||||||||||||||||||||||||||
образом, разложение в ряд Лорана в кольце 0 < | − 1| < 3 имеет вид
|
|
|
2 − 1 |
|
|
1 1 − 1 |
( |
)2 |
( |
− 1 |
)3 |
|
||||||
( |
) |
|
|
|
− 1 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= 2 + − 2 |
= − 1 + 3 − 9 + |
|
27 |
− |
81 |
+. .. |
||||||||||||
|
|
|
||||||||||||||||
|
1 |
|
|
|
|
( |
|
|
)−1 |
|
|
|
|
Слагаемое |
−1 |
является степенью |
− 1 |
|
и поэтому не требует |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
дальнейшего разложения. |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
( ) |
|
2 −3 |
|
Пример 4. Разложить в ряд Лорана функцию |
= |
2−4 +3 |
в |
||||||||||
окрестности ее особых точек. |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
( |
|
) |
: |
2 |
− 4 + 3 = 0, 1 |
= 1, 2 = 3. |
||||
Найдем особые точки функции |
|
|
|||||||||||
Получим разложение функции |
|
|
в |
окрестности точки 1 = 1. |
|||||||||
Ближайшая область аналитичности - |
кольцо 0 < | − 1| < 2. Число |
||||||||||||
2 найдено, как расстояние между центром разложения = 1 и
ближайшей особой точкой = 3.
Представим ( ) в виде суммы элементарных дробей

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 −3 |
= |
|
|
+ |
|
|
|
|
|
= |
1 |
|
∙ |
1 |
|
|
+ |
3 |
|
∙ |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2−4 +3 |
|
−1 |
−3 |
2 |
|
−1 |
2 |
|
−3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Сделаем замену: − 1 = , т.е. = + 1 и перепишем функцию |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 |
∙ |
1 |
|
+ |
|
3 |
∙ |
1 |
|
= |
|
1 |
∙ |
1 |
|
+ |
|
3 |
∙ |
1 |
|
= |
|
1 |
|
|
1 |
|
− |
3 |
∙ |
1 |
|
|
= |
1 |
|
|
1 |
− |
3 |
∙ |
1 |
|
= |
1 |
|
1 |
− |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
2 |
|
−1 |
|
|
2 |
−3 |
2 |
|
|
|
|
|
2 |
−2 |
|
2 |
|
|
|
2 |
|
2− |
|
2 |
|
|
|
4 |
|
1− |
|
|
2 |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
( −1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
∑∞=0 |
|
|
= |
|
|
|
|
− |
|
∑∞=0 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
4 |
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
2 |
|
4 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Область сходимости этого ряда 0 < | −21| < 1 или 0 < | − 1| < 2.
Получим разложение функции в окрестности точки 2 = 3.
Ближайшая область аналитичности - кольцо 0 < | − 3| < 2. Число
2 найдено, как расстояние между центром разложения = 3 и
ближайшей особой точкой = 1.

Сделаем замену: − 3 = , т.е. = + 3 и перепишем функцию
1 |
1 |
3 |
1 |
|
1 |
1 |
3 |
1 |
|
1 |
1 |
|
|
|
3 |
1 |
|
1 |
∑∞=0(−1) |
|
|
|
3 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
∙ |
|
|
|
+ |
|
∙ |
|
= |
|
∙ |
|
+ |
|
|
|
∙ |
|
= |
|
|
|
|
|
+ |
|
∙ |
|
= |
|
|
|
+ |
|
|
∙ |
|||||||||||
2 |
−1 |
2 |
−3 |
2 |
+2 |
2 |
|
4 |
1+ |
|
2 |
|
4 |
2 |
2 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
∑∞=0(−1) |
( −3) |
3 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
= |
|
|
|
+ |
|
∙ |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
4 |
|
2 |
2 |
−3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−3 |
|
|
|
|
|
|
|
|
| |
|
| |
|
|
|
|
|
||
Область сходимости этого ряда |
0 ≤ | |
2 |
| < 1 или 0 < |
|
− 3 < 2. |
|
|||||||||||||||||||||||||||||||||||||||||||
Пример 5. Разложить в ряд Лорана функцию ( ) = ( − 3)4 1
−3
в окрестности точки 0 = 3.
|
|
|
|
|
|
1 |
|
|
|
( ) |
|
1 |
|
|
Решение: |
сделаем замену |
= −3, получим |
= |
4 |
. |
|||||||||
|
||||||||||||||
Используя табличное разложение для функции cos : |
|
|
|
|
||||||||||
cos = 1 − |
2 |
+. . . +(−1) |
2 |
|
+. . . = ∑∞=0(−1) |
2 |
|
, получим |
||||||
2! |
(2 )! |
(2 )! |
||||||||||||
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
|
= 1 − |
|
|
|
1 |
|
|
+ |
|
|
|
|
1 |
|
|
− |
|
|
|
1 |
|
|
+. . ., |
|||||
− 3 |
2! |
( |
|
|
)2 |
4! |
( |
|
|
|
)4 |
( |
|
|
)6 |
||||||||||||||||
|
|
|
− 3 |
|
|
− 3 |
|
|
|
|
6! − 3 |
||||||||||||||||||||
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) |
( |
|
|
)4 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
(1 − |
|
|
( |
|
)2 + |
|
|
( |
|
|
|
)4 − |
|
( |
)6 + |
||||||||||||||
|
= − 3 |
2! |
|
4! |
|
|
|
6! |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
− 3 |
|
|
|
|
|
− 3 |
|
|
|
|
− 3 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
( |
|
)2 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|||||
|
|
) |
( |
|
|
)4 |
|
|
− 3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
+. . . |
|
|
− |
|
|
|
+ |
|
|
− |
|
|
( |
|
|
|
)2 +. .. |
|
||||||||||||
|
|
|
= − 3 |
|
2! |
|
|
4! |
6! |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 3 |
|
|
|
|
||||||||
Это разложение справедливо для любой точки ≠ 3. В данном случае «кольцо» представляет собой всю комплексную плоскость с
одной |
выброшенной точкой |
= 3. Его можно определить так: |
||||||
0 < |
| |
− 3 |
| |
< +∞. Здесь = 0, = +∞. В указанной области |
) |
– |
||
|
|
|
|
( |
|
|||
аналитическая.

1
Пример 6. Разложить в ряд Лорана функцию ( ) = 2− −6 в
окрестности точки 0 = 0.
Найдем особые точки функции ( ): 2 − − 6 = 0, 1 = −2,
2 = 3.
Области аналитичности функции:
а) | | < 2, б) 2 < | | < 3, в) | | > 3.
Представим функцию в виде суммы простейших дробей:
( ) = 15 ( −13 − +21 ).
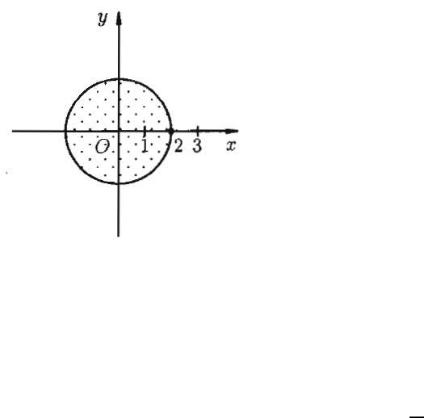
а) | | < 2 .
1 |
= − |
1 |
|
1 |
= − |
1 |
(1 + |
|
+ |
2 |
+ ) = − ∑∞=0 |
|
. |
|
|
|
|
|
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
+1 |
||
−3 |
3 |
1− |
|
3 |
3 |
3 |
|
3 |
|
|||||
|
|
|||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
Область сходимости ряда: |3| < 1, т. е. | | < 3.
|
1 |
|
1 |
|
1 |
|
|
1 |
|
|
2 |
|
|
|
|
− |
= − |
|
|
= − |
(1 − |
+ |
|
− ) = − ∑∞=0(−1) |
|
, |
|||||
+2 |
2 |
1+ |
|
2 |
2 |
22 |
2+1 |
||||||||
|
|
|
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
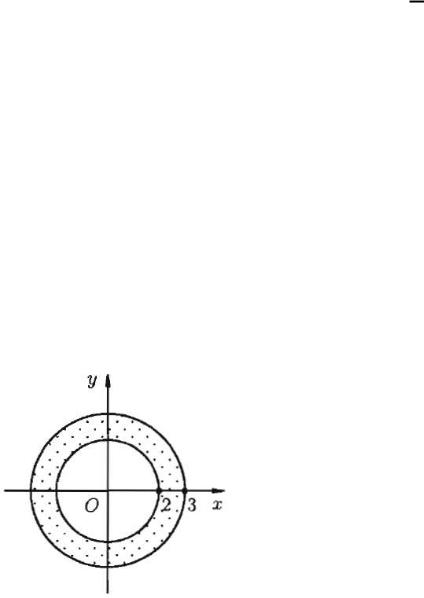
Область сходимости ряда: |2| < 1, т. е. | | < 2.
Следовательно,
( ) |
|
1 |
|
1 |
|
1 |
|
1 |
|
1 |
∑∞ |
1 |
|
1 |
|
|
||||
|
= |
|
= |
|
( |
|
− |
|
) = − |
|
|
=0 |
( |
|
+ (−1) |
|
|
) |
|
. |
2− −6 |
5 |
−3 |
+2 |
5 |
3+1 |
2+1 |
|
|||||||||||||
Ряд Лорана функции ( ) обращается в ряд Тейлора.
б) 2 < | | < 3, в этом кольце получим:
